恒压工作模式下光伏发电系统PI参数设计

刘少帅 张晓锋 夏益辉 李耕

摘  要： 光伏发电是利用太阳能资源的重要方式，当光伏阵列输出电能大于负载所需且蓄电池满充时，光伏发电系统转入恒压工作模式。针对光伏电池输出特性，推出光伏发电系统等效模型，根据恒压工作模式下系统控制框图，推导出控制电路传递函数，进而分析了光照强度、温度等环境因素以及元件寄生参数对系统稳定运行的影响，简化满足系统稳定运行要求的表达式，并计算出系统稳定时的PI参数范围。最后，通过Matlab仿真验证所求PI参数范围的正确性。

关键词： 恒压控制; 光伏发电系统; 稳定性; 寄生参数; 传递函数; PI参数

中图分类号： TN02?34; TM914                    文献标识码： A                      文章编号： 1004?373X（2020）21?0114?05

Design of PI parameter for photovoltaic power generation system

under constant voltage mode

LIU Shaoshuai， ZHANG Xiaofeng， XIA Yihui， LI Geng

（College of Electrical Engineering， Naval University of Engineering， Wuhan 430033， China）

Abstract： Photovoltaic power generation is an important way of solar energy resource utilization. When the output power of the photovoltaic array is greater than the load requirement and the battery is fully?charged， the photovoltaic power generation system is transformed to the constant voltage operation mode. According to the output characteristics of photovoltaic cells， the equivalent model of photovoltaic power generation system is proposed. And then， the transfer function of control circuit is derived on the basis of the system control block diagram under constant voltage operation mode. Furthermore， the influence of environmental factors such as light intensity， temperature and parasitic parameters of components on the stable operation of the system is analyzed， the expression meeting the requirements of stable operation of the system is simplified， and the PI parameter range when the system is stable is calculated. Finally， the correctness of the range of PI parameters is verified by Matlab simulation.

Keywords： constant voltage control; photovoltaic power generation system; stability; parasitic parameter; transfer function; PI parameter

0  引  言

光伏发电系统干净清洁、资源充裕，是新能源发电的重要组成部分[1?3]。为了最大限度地利用太阳能，需要通过控制手段实现光伏发电单元的最大功率跟踪[4]。然而，当光伏阵列输出电能大于负载所需且蓄电池满充时，光伏发电系统转入恒压工作模式。光伏阵列的输出特性与环境因素的变化呈非线性，会影响系统的稳定性，需要通过控制系统进行调节。PI调节器是控制系统的重要组成部分，在工程实践中，PI调节器通常用来改善系统的稳态性能。PI参数是PI调节器的关键环节，对系统稳定性有重要影响。因此，有必要对PI参数的选取展开研究。

通常情况下，在选取PI参数时，往往采用试凑法或者临界比例度法，不仅盲目性大、效率低，而且采用经验公式计算的方法误差大且不能适用于所有情况。有的文献通过加入零极点[5]或设定稳态性能指标[6?7]求取满足稳定要求的PI调节器参数，但都仅满足于某些具体情况，不具有普适性。文献[8]在建立了包含光伏电池动态模型的小信号模型基础上，分析了二极管动态电阻对系统稳定性的影响，分别计算出实际情况下、忽略二极管动态电阻情况下以及忽略光伏阵列等效内阻情况下的PI参数范围，但没有考虑电器元件寄生参数对系统稳定性的影响。文献[9]根据调节器参数变化对系统特征值轨迹的影响来设计参数，但是在研究时仅分析单个参数的影响，忽略了各参数之间的耦合关系，无法在整个系统中实现性能最优。文献[10]针对恒压模式下，对负载端输出电压相同的2个工作点的频域稳定性进行分析，得出恒压工作模式下系统工作于电压源区时稳定性更好。

本文首先推导出光伏发电系统控制电路传递函数，然后分析环境因素以及寄生电阻对系统稳定性的影响，简化满足系统稳定要求的表达式，并计算出PI参数范围。最后，通过Matlab仿真验证所求范围的正确性。

1  光伏发电系统结构

光伏电池输出伏安特性[11]为：

[IPV=ISC-ID-Ish=ISC-Ioexpq（UPV+IPV×Rs）AkT-1-UPV+IPV×RsRsh]

（1）

式中：[IPV]为光伏阵列输出电流;[ISC]为光生电流源电流;[ID]为光伏电池二极管电流;[Rs]为电池等效串联电阻;[UPV]为光伏阵列输出电压;[Io]为二极管饱和电流;[Rsh]为电池等效并联电阻;[T]为光伏电池工作绝对温度值;[k]为玻尔兹曼常量[12]，为1.381×10-23 J/K;[q]为电子的电荷，为1.602×10-19 C;[A]为二极管特性拟合系数。通常，[（UPV+IPV×Rs）Rsh?ISC]，因此忽略[（UPV+IPV×Rs）Rsh]项。式（1）可化简为：

[IPV=ISC-Ioexpq（UPV+IPV×Rs）AkT-1] （2）

根据式（2），光伏电池等效电路如图1所示。

图1中：[C1]为输入电容;[RC1]为输入电容寄生电阻;[IL]为电感电流;[L]为变换器升压电感;[RL]为电感寄生电阻;D为二极管;Q为开关管;[C2]为变换器输出电容;[RC2]为输出电容寄生电阻;[Uo]为负载端电压;[R]为负载端电阻。[Re]为光伏电池等效内阻[13]，表示为：

[Re=UPVISC-IPV] （3）

2  控制系统结构及稳定条件

2.1  变换器状态空间模型及传递函数

通过建立系统小信号模型，推导出系统内部变量之间的关系，可为PI参数设计提供参考。光伏发电系统中常用的Boost变换器小信号状态方程为：

[L?diL（t）dt=uPV（t）-iL（t）RL-（1-D）uo（t）+d（t）UoC1?duC1（t）dt=iSC（t）-uPV（t）Re-iL（t）RC1C1?duC1（t）dt=uPV（t）-uC1（t）C2?duC2（t）dt=（1-D）iL（t）-uo（t）R-d（t）ILRC2C2?duC2（t）dt=uo（t）-uC2（t）] （4）

式中：[iL（t）]，[iSC（t）]，[iPV（t）]，[uPV（t）]，[uo（t）]，[d（t）]分别为[iL（t）]，[iSC（t）]，[iPV（t）]，[uPV（t）]，[uo（t）]，[d（t）]的扰动量。

对式（4）进行拉氏变换可得：

[sLiL（s）=uPV（s）-iL（s）RL-（1-D）uo（s）+Uod（s）sC1uC1（s）=iSC（s）-1ReuPV（s）-iL（s）sRC1C1uC1（s）=uPV（s）-uC1（s）sC2uC2（s）=（1-D）iL（s）-1Ruo（s）-ILd（s）sRC2C2uC2（s）=uo（s）-uC2（s）] （5）

整理可得负载端输出电压与占空比之间的传递函数为：

[Guod=Uod=A0s4+A1s3+A2s2+A3s+A4B0s4+B1s3+B2s2+B3s+B4] （6）

式（6）中系数表达式如表1所示。

2.2  控制系统结构及稳定条件

恒压控制系统结构图如图2所示，[Uo，ref]为光伏发电系统负载端参考电压。该控制系统是单闭环结构，负载端实际输出电压与负载端参考电压作差比较后，经过PI调节器进行调节，再经PWM调制器调整占空比的大小，使负载端实际输出电压为参考电压，从而实现恒压控制。系统控制结构框图如图2所示。

由图2可得，恒压工作模式下系统闭环传递函数为：

[?o（s）=Fmo?Gpi（s）?Guod（s）1+Fmo?Gpi（s）?Guod（s）] （7）

式中：[Gpi（s）]为PI调节器，[Gpi（s）=kp+kis];[Fmo]为PWM调制器增益，由于恒压工作模式下光伏阵列的稳定区通常选择电压区[9]，[Fmo]取正。根据式（7）可得系统闭环特征方程，再根据劳斯判据即可列写系统稳定条件表达式。

3  稳定条件参数分析

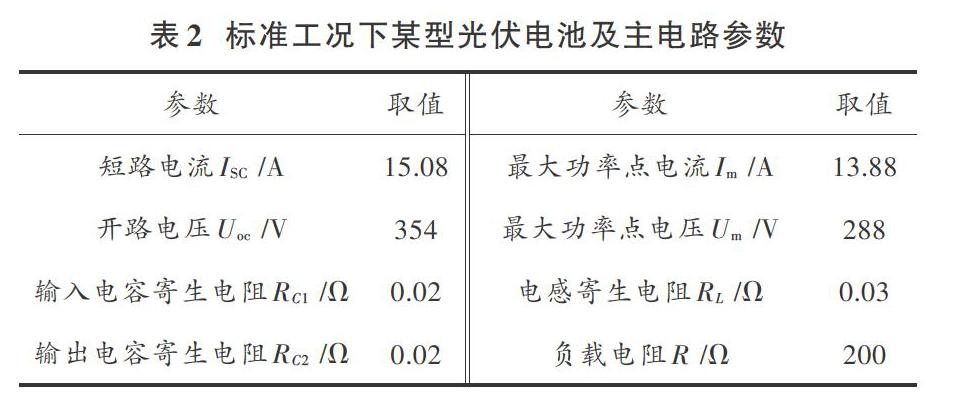
由表1和式（7）可知，要求出满足系统稳定条件的解析表达式非常困难，不失一般性，采用表2所示参数代入计算，求满足系统稳定要求的数值解。其参数设置如表2所示。

3.1  环境因素对系统稳定性影响分析

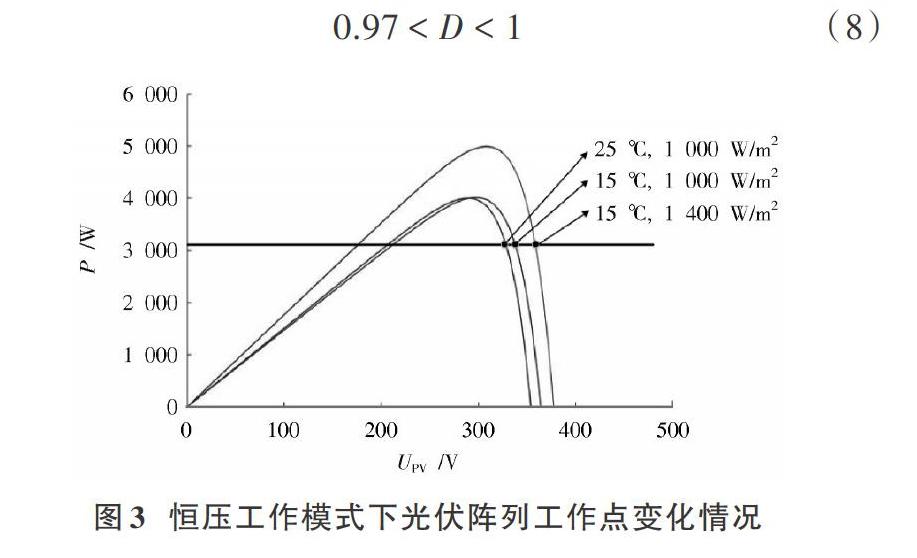
由光伏发电系统输出特性知，光伏阵列的输出特性与环境变化不是线性关系。不同光照和环境温度下，光伏阵列输出情况如图3所示。

由图3知，当负载端输出电压恒定时，随着温度升高或光照强度变弱，光伏阵列输出电压逐渐减小。为便于分析，假設在某一稳态下，[Uo=]400 V，[ISC=]15.08 A，[Fmo=1]，采用表2所示参数和图2所示控制结构参与计算。经前期试凑可知，当[kp=0.01]，[ki=6]时，光伏发电系统能够稳定运行于恒压工作模式。根据劳斯判据，可得系统稳定条件为：

[0.97

当PI参数取其他数值时，可得到[Y1

3.2  寄生参数对系统稳定性影响分析

为便于分析寄生参数对系统稳定性的影响，假设某一稳态下，[Uo=]400 V，[UPV=]350 V，[D=0.13]，[ISC=]15.08 A，[kp=]0.01，[ki=6]，采用表2所示参数和图2所示控制结构，将输入电容寄生电阻值设为变量，可得系统稳定条件为：

[RC1>-0.31 Ω] （9）

当PI参数取其他数值时，得到输入电容寄生电阻的取值范围为：[RC1>Y2]，[Y2<0]。即不同稳态PI参数下，系统稳定运行于恒压工作模式的条件为[RC1]的值大于一个负数，而实际情况下，[RC1≥0]。因此，输入电容寄生电阻参与系统稳定性计算时，可以假定[RC1=0]。

同样地，将电感寄生电阻[RL]设为变量，系统稳定条件为：-0.58<[RL]<128.94。换其他PI参数，得到电感寄生电阻的取值范围为：[Y3]<[RL]<128.94，[Y3]<0。即不同稳态PI参数下，系统稳定运行于恒压工作模式的条件为[RL]的值大于一个负数且小于128.94 Ω，而实际情况下，[0≤RL?]128.94 Ω。因此，电感寄生电阻参与系统稳定性计算时，可以假定[RL]=0。

将输出电容寄生电阻设为变量，系统稳定条件为：-0.06<[RC2]<56.78。换其他PI参数，得到输出电容寄生电阻的取值范围为：[Y40。即不同稳态PI参数下，系统稳定运行于恒压工作模式下的条件为[RC2]的值大于一个负数且小于一个正数，而实际情况下，[RC2]≥0。因此，输出电容寄生电阻参与系统稳定性计算时，可以假定[RC2]=0。

综上分析，输入电容寄生电阻、电感寄生电阻、输出电容寄生电阻参与系统稳定性计算时，均可以假定为0。

3.3  控制系统PI参数设计

根据3.1节和3.2节分析可知，在最强光照、最低温度和输入电容寄生电阻、电感寄生电阻、输出电容寄生电阻均为0的条件下，设计恒压工作模式光伏发电控制系统参数，可使系统获得较好的稳定性。

当输入电容寄生电阻、电感寄生电阻、输出电容寄生电阻均为0时，恒压工作模式控制系统闭环特征方程为：

[RC1C2LReS4+（C1LRe+C2RL-ILLRC1kpRe）s3+[（1-D）2RC1Re+RC2ReL-ILLRC1kiRe+（1-D）RC1ReUokp-ILLRkp]s2+[（1-D）2R+Re-ILRRekp+（1-D）RUokp+（1-D）RC1ReUoki-ILLRki]s+（1-D）RUoki-ILRkiRe=0                                                 （10）]

假定光照强度最大为1 400 W/m2，温度最低为15 ℃，某一稳态下光伏发电系统输出情况为[Uo=]400 V，[UPV=]356 V，[D=]0.11，[Io=]2 A，[R=]200 Ω，[Re]=19.42 Ω。根据劳斯判据，解得系统稳定时PI参数选择范围如图4所示。

4  仿真验证

在Matlab/Simulink环境下，采用表2所示参数，搭建光伏发电系统恒压工作模式下的仿真模型。

4.1  传递函数稳定性计算

在图4中任取一点，如取[kp=]0.02，[ki=4]，可得此時系统幅值裕度为1.41 dB，相角裕度为2.01°，即幅值裕度和相角裕度均为正。闭环特征方程根分别为[s1=]-553，[s2=]-202，[s3，4=]-37.6±3 400*[i]，即闭环特征方程根均为负。根据自动控制原理理论可知，该PI参数下的系统能够稳定运行于恒压工作模式。

4.2  仿真结果及分析

取[kp=]0.02，[ki=]4，假定光照强度变化范围为600～1 400 W/m2，温度变化范围为15～35 ℃，分别观察系统在光照强度变化、温度变化、有无寄生参数时的输出情况。

假设环境温度为25 ℃不变，0～0.4 s时，光照强度为1 400 W/m2;0.4～0.8 s时，光照强度为1 000 W/m2;0.8～1.2 s时，光照强度为600 W/m2。图5a）为光照强度变化时，光伏发电系统负载端输出电压波形。假设光照强度为1 000 W/m2不变，0～0.4 s时，环境温度为35 ℃;0.4～0.8 s时，环境温度为25 ℃;0.8～1.2 s时，环境温度为15 ℃。图5b）为温度变化时，光伏发电系统负载端输出的电压波形。

标准工况下（光照强度为1 000 W/m2，温度为25 ℃），不考虑寄生参数时，光伏发电系统负载端输出电压波形如图6所示。

在标准工况下考虑寄生参数时，取输入电容寄生电阻[RC1=]0.02 Ω，电感寄生电阻为[RL=]0.03 Ω，输出电容寄生电阻[RC2=]0.02 Ω，光伏发电系统负载端输出电压波形如图7所示。

对以上仿真结果进行整理，结果如表3所示。

由表3可知，在最强光照强度和最低温度条件下计算得到的PI参数能够在其他光照和温度条件下保持系统的稳定运行;在不考虑寄生参数情况下计算得到的PI参数能够适用于含寄生参数电路，与3.1节和3.2节分析结果相吻合。

5  结  论

本文分析了环境因素以及寄生参数对系统稳定运行的影响，简化了满足系统稳定要求的表达式，计算出系统稳定运行时的PI参数范围，最后通过Matlab仿真进行验证。结果表明：

1） 光照强度越强或者温度越低，系统越不容易稳定，此时计算得到的PI参数能够在其他光照和温度条件下保持系统的稳定运行;

2） 输入电容寄生电阻、电感寄生电阻、输出电容寄生电阻参与系统稳定性计算时，均可以取0;

3） 通过Matlab仿真验证可知，计算得到的PI参数范围能够满足恒压工作模式下光伏发电系统稳定运行的需要。

本文的研究可以增强PI参数选取的科学性，同时，简化恒压工作模式下光伏发电系统稳定条件的计算过程，为开展光伏发电系统其他方面的研究打下基础。

参考文献

[1] BOROYEVICH D， CVETKOVIC I， DONG Dong， et al. Future electronic power distribution systems a contemplative view [C]// IEEE Conference on Optimization of Electrical and Electronic Equipment. Brasov， Romania： IEEE， 2010： 1369?1380.

[2] 刘念，唐霄，段帅，等.考虑动力电池梯次利用的光伏换电站容量优化配置方法[J].中国电机工程学报，2013，33（4）：34?44.

[3] FEMIA N， FORTUNATO M， VITELLI M. Light?to?light： PV?fed LED lighting systems [J]. IEEE transactions on power electronics， 2013， 28（8）： 4063?4073.

[4] 肖文波，余晓鹏.光伏系统功率跟踪算法的仿真平台设计及其实现[J].现代电子技术，2019，42（12）：104?107.

[5] 王生铁，贾立宾，张计科，等.双级式光伏并网发电前级变换器系统建模与控制器参数设计[J].可再生能源，2016，34（3）：360?367.

[6] 任明炜，孙玉堂，嵇小辅.数据可视化的LCL型并网逆变器PI参数设计[J].电力电子技术，2016，50（8）：44?47.

[7] 郑鹤玲，毕大强，葛宝明.光伏模拟系统建模与控制器参数优化[J].电力系统保护与控制，2011，39（18）：49?55.

[8] 秦岭，谢少军，罗松.恒压充电模式下独立光伏储能系统的鲁棒稳定控制器设计[J].中国电机工程学报，2018，38（12）：3451?3460.

[9] HUANG Hanqi， MAO Chengxiong， LU Jiming， et al. Small?signal modeling and analysis of grid?connected photovoltaic ge?neration systems [J]. Proceedings of the CSEE， 2012， 32（22）： 7?14.

[10] 侯世英，殷忠宁，薛原，等.独立光伏系统恒压工作模式下最优工作区的选择[J].电网技术，2012，36（6）：226?231.

[11] 张兴，曹仁贤.太阳能光伏并网发电及其逆变控制[M].北京：机械工业出版社，2018.

[12] 代相波，赵志刚.基于滞环比较的扰动观测法在光伏MPPT中的研究[J].沈阳工程学院学报（自然科学版），2018，14（1）：5?10.

[13] 杨梅.单相光伏并网逆变系统研究与设计[D].马鞍山：安徽工业大学，2016.

作者简介：刘少帅（1992—），男，河南人，硕士研究生，研究方向为电力电子与电力传动。

张晓锋（1963—），男，江苏人，教授，博士生导师，研究方向为电力系统及其自动化、电力电子与电力传动。

夏益辉（1987—），男，河南人，博士，讲师，研究方向为电力电子与电力传动。

李  耕（1987—），男，湖北人，博士，讲师，研究方向为电力系统运行保护。