基于混沌分析算法的高校毕业生就业率预测


摘 要: 由于高校毕业生就业率与多种因素相关,具有复杂的变化规律,当前高校毕业生就业率预测模型存在一定的不足,如与实际值间的偏差大,建模时间长等,为了减少高校毕业生就业率预测误差,设计了一种基于混沌分析算法的高校毕业生就业率预测模型。首先,收集高校毕业生就业率的历史数据,结合历史数据的随机性、混沌性变化特点,采用混沌分析算法对历史数据的随机性、混沌性变化特点进行分析,重构高校毕业生就业率的历史数据;然后,引入当前最流行的数据挖掘技术——最小二乘支持向量机构建高校毕业生就业率的历史数据模型;最后,在相同平台上与当前经典高校毕业生就业率预测模型进行对比测试。结果表明,混沌分析算法的高校毕业生就业率预测值与实际值之间的偏差相当小,高校毕业生就业率预测精度超过94%,而经典模型的高校毕业生就业率预测精度处于90%左右,同时混沌分析算法减少了高校毕业生就业率预测的建模时间,可以满足现代高校毕业生就业率数据向大规模发展方向的要求。
关键词: 毕业生就业率; 预测精度; 数据挖掘技术; 经典模型; 随机性变化特点; 混沌分析算法
中图分类号: TN911.1?34; TP391 文献标识码: A 文章编号: 1004?373X(2020)21?0101?05
College graduate employment rate prediction model based on chaos analysis algorithm
ZHANG Yingnan
(Jilin Agricultural University, Changchun 130000, China)
Abstract: For the college graduate employment rate is related with several factors and has complex changing rules, the current prediction model of the college graduate employment rate has some deficiencies, like large deviation from the actual values, long modeling duration, etc. In view of the above, a college graduate employment rate prediction model based on chaos analysis algorithm is designed to reduce the prediction error of the college graduate employment rate. The historical data of the college graduate employment rate are collected. The chaos analysis algorithm is used to analyze the characteristics of randomness and chaos of the historical data for the data reconstruction. And then, the most popular data mining technology named least square support vector machine is introduced for the model of the historical data of college graduate employment rate. Finally, comparative tests are performed on the same platform to compare the proposed model with the current classic employment rate prediction model. The results show that the deviation between the predicted value and the actual value of the college graduate employment rate by the chaos analysis algorithm is quite small, and the prediction accuracy of the college graduate employment rate exceeds 94%, while the prediction accuracy of the classic model is about 90%. At the same time, the chaos analysis algorithm can reduce the modeling duration of the prediction model, which meets the requirements of large?scale development of modern college graduate employment rate data.
Keywords: graduate employment rate; prediction accuracy; data mining technology; classic model; random change characteristics; chaos analysis algorithm
[f(x)=ωTφ(x)+b] (10)
式中[ω]和[b]分别为权值和偏置量。
基于最小二乘支持向量机的建模原理,引入松弛变量[ek]弱化高校毕业生就业率预测误差,这样可以得到一个如式(11)等价的形式,具体如下:
[minω,b,eJp(ω,e)=12ω2+12γi=1ne2is.t. yi=ωTφ(xi)+b+ei, i=1,2,…,t] (11)
式中[γ]表示正则化参数。
引入[αi]为拉格朗日乘子,加快高校毕业生就业率预测建模效率,得到的拉格朗日函数为:
[L(ω,b,e,α)=J(ω,e)-i=1nαi(ωTφ(xi)-b+ei-yi)] (12)
消去[ω]和[e]后,构建矩阵形式,具体为:
[0ITtItΩ+1γItbα=0y] (13)
采用核函数替代内积操作,即[K(xi,xj)=φT(xi)φ(xj)],最小二乘支持向量机的高校毕业生就业率预测函数为:
[f(x)=i=1NαiK(x,xi)+b] (14)
1.3 混沌分析算法的高校毕业生就业率预测步骤
Step1:对具体高校毕业生就业率的历史数据进行收集,并通过一些专家对数据进行分析,去掉一些错误数据,并对错误数据采用平均化方法进行补齐。
Step2:采用混沌分析算法中的关联积分确定高校毕业生就业率数据的嵌入维和时间延迟。
Step3:采用嵌入维和时间延迟对原始高校毕业生就业率数据进行重构,得到一个多维的高校毕业生就业率数据。
Step4:根据一定的比例将多维高校毕业生就业率数据划分为训练集和验证集。
Step5:最小二乘支持向量机对高校毕业生就业率数据的训练集进行学习,并通过留一法确定最小二乘支持向量机的参数,从而建立高校毕业生就业率预测模型。
Step6:采用验证集对高校毕业生就业率预测模型的性能进行分析,如果预测满足实际应用要求,就可以对未来几年的高校毕业生就业率进行预测,并将预测结果提供给高校的相关部门,为他们决策提供有价值的参考意见。
2 实例分析
2.1 高校毕业生就业率预测的分析平台
为了检测混沌分析算法的高校毕业生就业率预测效果,需要设计预测实验,本文选择的测试平台如表1所示。在相同测试平台下,选择当前经典高校毕业生就业率预测模型进行对照测试,它们分别为最小二乘支持向量机的高校毕业生就业率预测模型(LSSVM)和BP神经网络高校毕业生就业率预测模型(BPNN),LSSVM的建模数据没有经过混沌处理,采用原始高校毕业生就业率数据直接建模;BPNN对原始高校毕业生就业率数据进行混沌分析,然后采用BP神经网络进行建模。
2.2 高校毕业生就业率历史数据
为了体现高校毕业生就业率预测结果的公平性,选择5所类型不同的高校毕业生就业率历史数据作为测试对象,具体如表2所示。
2.3 高校毕业生就业率历史数据的混沌分析
采用上述混沌分析算法对表2的5所类型不同的高校毕业生就业率历史数据进行分析,计算嵌入维和时间延迟,具体如表3所示。从表3可以看出,5所高校毕业生就业率历史数据的嵌入维和时间延迟各不相同,这表明5所高校毕业生就业率变化特点不完全相同,但是均具有混沌性和随机性,根据表3的嵌入维和时间延迟重构5所高校毕业生就业率历史数据,重构高校毕业生就业率预测学习样本。从重构的高校毕业生就业率预测学习样本选择500个样本作为验证样本,其他作为测试样本。
2.4 高校毕业生就业率预测结果分析
由于高校毕业生就业率建模主要是为了描述将来高校毕业生就业率变化情况,因为只采用一步预测没有太多的实际价值,因此本文进行一步和多步的高校毕业生就业率预测,统计的一步和多步的高校毕业生就业率预测精度结果分别如图2和图3所示。
对图2和图3的一步和多步的高校毕业生就业率预测精度进行分析可以发现:
1) 相对于一步高校毕业生就业率预测精度,多步的高校毕业生就业率预测精度有所降低,这是因为多步预测有误差累计效果,使得高校毕业生就业率预测误差不断增加。
2) 最小二乘支持向量机的高校毕业生就业率预测精度不高于90%,这是因为其没有引入混沌分析算法,最小二乘支持向量机采用原始高校毕业生就业率数据直接建模,无法准确描述高校毕业生就业率的变化特点,使得最小二乘支持向量机的高校毕业生就业率预测错误比较大。
3) BP神经网络的高校毕业生就业率预测精度也处于90%左右,这是因为虽然引入了混沌分析算法对原始高校毕业生就业率数据进行重构,但是BP神经网络的学习能力有限,经常得到局部最优,使得高校毕业生就业率预测错误结果不稳定,出现多个错误比较大的点,使得高校毕业生就业率整体预测精度不高。
4) 在所有模型中,本文模型的高校毕业生就业率预测精度最高,单步预测精度超过95%,多步預测精度超过92%,高校毕业生就业率预测误差小于当前的经典模型。这是因为本文模型不仅引入了混沌分析算法对原始高校毕业生就业率数据进行重构,同时采用学习能力更强的最小二乘支持向量机对高校毕业生就业率数据进行学习,可以更好地描述高校毕业生就业率变化特点,提高了高校毕业生就业率整体预测精度,实验结果验证了本文高校毕业生就业率预测模型的优越性。
2.5 高校毕业生就业率建模时间对比
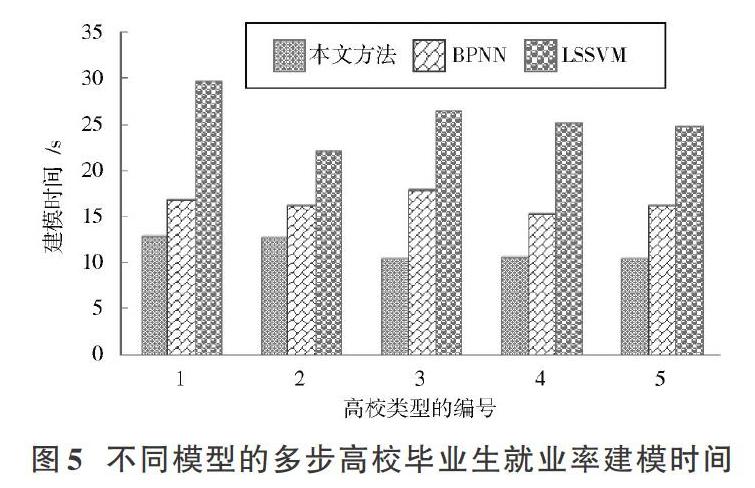
统计3种模型对5所高校毕业生就业率建模时间,分别统计一步和多步高校毕业生就业率建模时间,结果分别如图4和图5所示。
对图4和图5的一步和多步高校毕业生就业率建模时间进行对比和分析可以发现,无论是一步和多步预测,本文模型的高校毕业生就业率建模時间均要少于经典模型,提升了高校毕业生就业率建模速度,可以满足大规模高校毕业生就业率数据的建模与分析,具有更加广泛的实际应用范围。
3 结 语
高校毕业生就业率预测有利于帮助高校毕业生管理者制定相应的计划,受到了当前多所高校的高度关注。但是高校毕业生就业率与多种因素密切相关,各种因素之间又相互联系,变化规律十分复杂,使得当前高校毕业生就业率预测模型无法全面、准确地描述该变化特点。为了减少高校毕业生就业率预测误差,提升高校毕业生就业率预测速度,本文设计了一种基于混沌分析算法的高校毕业生就业率预测模型,并通过对比实验分析该高校毕业生就业率预测模型的有效性和优越性,同时为其他相似问题提供了一种有效的建模思路。
参考文献
[1] 武毅英.我国高校毕业生就业率预警线之探讨[J].江苏高教,2007(6):61?64.
[2] 金大伟,张明健.改进高校毕业生就业率统计方法初探[J].辽宁教育研究,2007(4):99?101.
[3] 胡宇辰.试论建立我国高校毕业生就业率统计的监督机制[J].社会科学研究,2005(2):189?191.
[4] 杨学坤,吴树勤.高校毕业生就业率统计的科学方法研究:从区别“就业率统计”和“就业状况估计”两个不同概念出发[J].甘肃社会科学,2004(6):133?135.
[5] 张学敏,柴晓旭.我国高校毕业生就业率与高校教育质量评价研究[J].东北师大学报(哲学社会科学版),2019(3):131?141.
[6] 张稳,恰汗·合孜尔.毕业生就业率预测及质量评估研究[J].计算机工程与科学,2009,31(5):141?143.
[7] 邹治,陈万明.高校毕业生就业率的解读与就业预警线的重构:以江苏省高校相关数据为证[J].现代教育科学,2009(2):1?5.
[8] 曲娜,化存才.高校毕业生就业率的一个微分方程定量模型[J].云南大学学报(自然科学版),2007(z1):24?26.
[9] 亓红强,张福堃,高大鲲,等.基于灰色系统的大学生就业率预测[J].现代电子技术,2019,42(11):174?177.
[10] 王先述.基于Cramer法则和ARMA模型的我国高校毕业生就业预测[J].统计与决策,2010(22):97?99.
[11] 程昌品,陈强.基于信息增益比的决策树用于毕业生就业预测[J].计算机仿真,2010,27(2):299?302.
[12] 苏变萍,王婧,王一平.改进BP神经网络及其在陕西就业预测中的应用[J].数学的实践与认识,2006,36(9):271?275.
[13] 钟仪华,林旭旭,刘雨鑫.基于多元混沌时间序列的油田产量预测模型[J].数学的实践与认识,2016,46(6):99?105.
[14] 雷苗,彭宇,彭喜元.面向混沌时间序列预测的隐式特征提取算法[J].仪器仪表学报,2014,35(1):1?7.
[15] 董春娇,邵春福,李娟,等.基于混沌分析的道路网交通流短时预测[J].系统工程学报,2011,26(3):340?345.
作者简介:张英楠(1989—),男,吉林松原人,硕士,助教,研究方向为思想政治教育。

