地震-桥梁-汽车耦合作用下行车安全性研究
李承宬
(上海矩尺土木科技有限公司, 上海 200092)
我国属于地震多发区域, 各地大大小小的地震时常被报道, 历史上也曾出现过多次灾难性地震。 但目前为止尚未有成熟的预测方法可以使人们有效躲避地震。 传统的桥梁抗震设计关注于桥梁的结构安全性。 然而桥梁结构并不是一个孤立系统, 在常遇地震荷载作用下, 在保证桥梁结构的安全性及正常功能不受影响的同时, 桥上的行车安全性也应受到重视[1~4]。 对于运输干路上的桥梁, 其上持续密集的车流已成常态, 由于地震的突发性和不可预测性, 地震作用下剧烈的桥面运动使得行驶中的车辆难于控制, 易造成交通事故。 基于此, 本文给出了一种求解地震-桥梁-汽车系统空间耦合振动问题的分析模型, 并开发了相应的分析程序, 然后以一组连续梁桥为对象,对突发地震状况下车辆侧滑或侧倾可能性等行车安全性问题进行了分析研究。
1 地震-桥梁-汽车耦合系统分析模型
1.1 车桥耦合系统模型
车桥耦合系统由两个子系统组成, 车辆子系统和桥梁子系统。 汽车在桥上行驶时会对桥梁产生动力作用, 从而引起桥梁结构的振动。 桥梁的振动也会对其上行驶的汽车产生动力作用, 从而影响车辆的行驶。 这种相互影响、 相互作用的现象就称为车桥耦合振动[5~7]。
桥梁子系统通常采用离散结构有限元方法建立模型。 其动力平衡方程可表示为:

其中, ub表示桥梁结构位移向量, Mb表示桥梁总体质量矩阵, Cb表示桥梁总体阻尼矩阵, Kb表示桥梁总体刚度矩阵, Fb表示作用于桥梁的外荷载向量。 采用Rayleigh 阻尼, 即Cb=αMb+βKb。
车辆子系统由车轮、 车轴、 车体等刚体构件和弹性连接件组成。 根据达朗贝尔原理, 以车辆在重力作用下的平衡位置作为基准, 可以建立车辆的动力平衡方程。

其中, uv表示车辆整体位移向量, Mv表示车辆整体质量矩阵, Cv表示车辆整体阻尼矩阵, Kv表示车辆整体刚度矩阵, Fv表示车辆外部激励荷载向量。
车桥耦合系统的运动方程可表示为:

其中, ub(t)和ub(t)分别表示在t 时刻桥梁结构和车辆的位移向量, Fb_G和Fv_G分别表示桥梁结构和车辆承受的重力荷载向量, Fb_v(t)和Fv_b(t)表示在t 时刻桥梁结构和车辆之间的相互作用力向量。采用分离迭代法进行求解系统运动方程。
1.2 车辆模型
车辆动力学模型一般将车轮、 车轴、 车体等视为刚体。 以两轴四轮车辆为例, 一个车辆由5个刚体元件组成, 包括1 个车体和4 个车轮。 刚体间通过弹簧元件和阻尼元件连接。 每个车轮对有横向位移和竖向位移两个独立的自由度。 车体具有5 个自由度, 分别是横向位移, 竖向位移,侧倾转动, 俯仰转动和竖向转动[5~7]。 车辆模型如图1 所示。
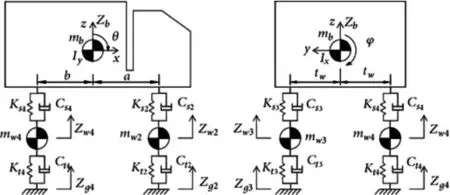
图1 车辆模型示意图
图中, Zb、 φ、 θ 分别为车体竖向位移、 侧倾转角及俯仰转角; mb、 lx、 ly分别为车体质量、 侧倾转动惯性矩和俯仰转动惯性矩; mwi、 Zwi分别为车轮的等效质量和竖向位移; Ksi、 Csi分别为悬架等效刚度和阻尼; Kti、 Cti分别为车轮轮胎等效刚度和阻尼; Zgi为轮胎底部位移。
根据李小年[6]相关研究数据, 建立使用与车桥耦合振动计算的各类标准车辆模型。 表1 给出了其中一类总重约45t 的车辆参数数据。
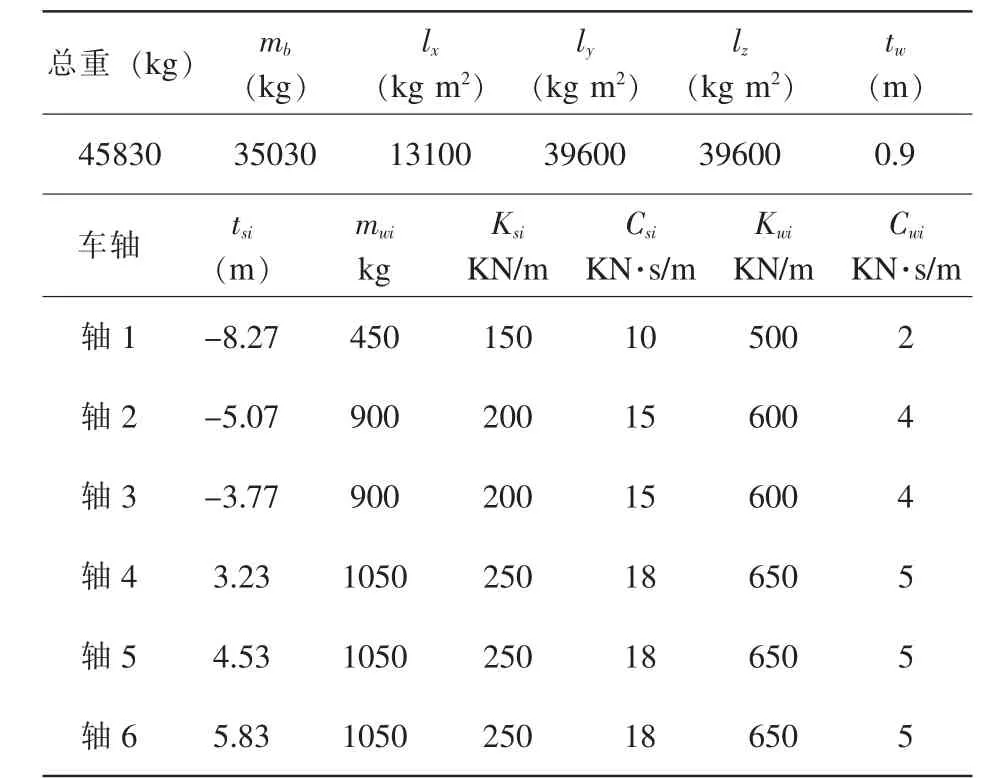
表1 典型车辆计算参数
1.3 路面粗糙度
车轮与桥梁路面的接触要考虑路面粗糙度的影响。 路面粗糙度是指路表相对于基准平面的偏离。 路面粗糙度一般假定为满足零均值的平稳各态历经的高斯随机过程, 可通过路面粗糙度功率谱密度函数模拟得到不同路面等级状况下其沿桥梁纵向分布函数[8]:
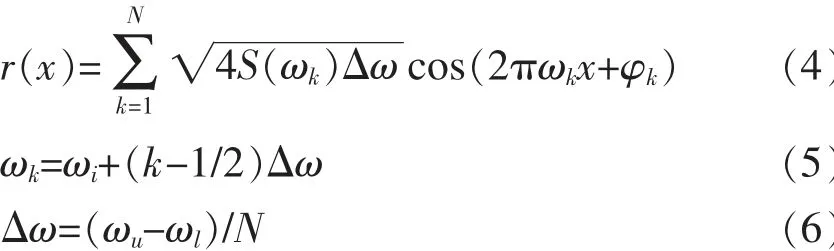
其中, r(x)表示桥面沿纵向不平整度值, Δω 表示空间频率变化步长, φk表示随机相位值, N 表示参与叠加的函数数量。 S(ωk)表示桥面不平整度功率谱密度函数,

式中, β 表示频率指数, 一般取1.94; ωk表示空间频率, ωl和ωu表示进行叠加的空间频率上限与下限。 α 表示路面粗糙度系数, 根据桥面不同粗糙度等级确定, 按照 ‘好’, ‘良好’, ‘普通’,‘较差’ 和 ‘差’ 五个级别, 其参考取值分别为0.12, 0.62, 2.5, 10 和20 (e-6 m2cycle/m)。
1.4 地震-桥梁-汽车耦合系统模型
此次研究建立的地震-桥梁-汽车耦合系统模型中, 将地震荷载施加于桥梁子系统上, 按照车辆和桥梁两个子系统建立分析模型。 地震荷载输入采用加速度时程, 以地面激励的形式施加于桥梁结构上。 车桥竖向接触单元模型采用非线性的只受压单元模型建立, 以考虑车轮脱离路面的情况。 该耦合系统的运动方程可表示为:
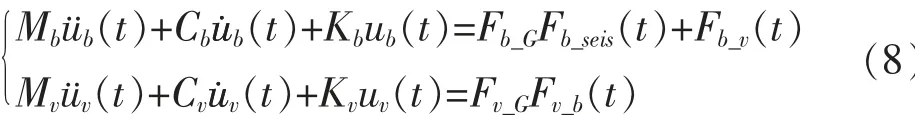
其中, t 表示时间, Fb_seis(t)表示桥梁结构在t 时刻承受的地震荷载向量, ub(t)、 uv(t)及uh&s(t)分别表示在t 时刻桥梁结构、 车辆和人椅系统的位移向量, Fb_G、 Fv_G及Fh&s_G分别表示桥梁结构和车辆承受的重力荷载向量, Fb_v(t)和Fv_b(t)表示在t 时刻桥梁结构和车辆之间的相互作用力向量。
该系统运动方程采用分离迭代法进行求解,其求解步骤为: (1) 对于时刻t1, 以前一时刻t0的桥梁子系统的运动状态Ub(t0)和车辆子系统的运动状态Uv(t0)作为初始值; (2) 计算得到车辆在t1时刻所在位置的路面粗糙度, 计算车辆子系统外部激励荷载向量; (3) 采用HHT 方法求得车辆在t1时刻的响应Uv(t1), 并计算得到车辆各车轮对桥梁的作用力; (4) 根据t1时刻的地震荷载输入, 以及上一步得到的车辆对桥梁的作用力, 更新桥梁子系统外部激励荷载向量; (5)采用HHT 方法求解t1时刻桥梁结构的瞬时动力响应Ub(t1); (6) 计算桥梁与车辆的几何耦合关系和力学耦合关系情况, 如满足误差要求, 则进行下一时刻t2的计算; 如不满足要求, 则以计算得到的Ub(t1)和Uv,h(t1)作为新的初始值重复步骤(2) ~(6)。
2 行车安全性分析
2.1 桥梁工程介绍
目标桥梁为一组多跨预应力混凝土连续T 梁桥 (如图2 所示), 总长600m, 其跨径布置为40m×15=600m, 中间为三联4 跨连续梁, 一端为简支梁, 另一端为一联2 跨连续梁。 主梁宽12.5m, 梁高2.5m, 横桥向由5 片T 梁组成。 桥墩均采用独柱式空心薄壁墩, 纵桥向宽3m, 横桥向宽6m, 平均墩高约50m。 根据地震安评报告, 工程场地地震动参数如表2 所示, 地震动时程曲线如图3 所示。

图2 多跨连续梁桥立面布置示意图

表2 工程场地地震动参数 (E1)
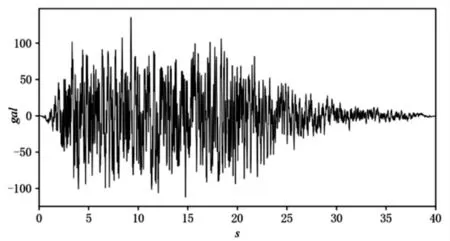
图3 设计地震动时程曲线 (E1)
2.2 分析工况介绍
研究关注于突发地震情况下桥上车辆在行进过程中出现侧滑或侧倾的可能性, 考虑20、 40和60km/h 三种不同车速及 ‘好’ ‘普通’ 和‘差’ 三种不同路面粗糙度的影响。 计算分析则采用自行开发的基于通用有限元计算软件ANSYS的车桥耦合计算程序进行。 加载方案为在一列由典型车辆组成的重车车队匀速通过目标桥梁结构的过程中同步输入地震荷载。 以6 轴45t 重的标准车辆作为典型车辆(具体参数见表1), 车头间距60m。 地震荷载输入开始时, 各车均处于行驶状态。 地震荷载仅考虑E1 级横竖向地震动输入组合。
2.3 车桥间竖向作用力分析
根据计算结果, 地震作用下的车桥间竖向作用力的波动幅度会放大, 该放大效应与路面粗糙度相关。 相同车速下, 路面粗糙度低时波动幅度放大效应显著, 而路面粗糙度高时则不显著。 为便于分析, 定义地震荷载输入20s 后位于桥梁全长中点位置处的典型车辆为1 号车。 图4 和图5分别给出了路面粗糙度等级 ‘好’ 与 ‘普通’ 状况下1 号车在有无地震荷载输入时车桥间竖向力随桥长的变化曲线 (车速60km/h)。 可看出, 当路面粗糙度等级为 ‘好’ 时地震作用下的车桥间竖向作用力的波动幅度显著放大, 但路面粗糙度等级为‘普通’ 时仅略有放大。
对比各工况结果发现, 车桥间竖向作用力的波动幅度与路面粗糙度的相关性较高, 而与车速大小的相关性较低。 图6 给出了1 号车在地震作用下相同车速 (60km/h) 不同路面粗糙度状况时车桥间竖向作用力随桥长的变化曲线。 可看出,路面粗糙度越高, 车桥间竖向作用力的波动幅度越大, 趋势十分显著。 图7 给出了1 号车在地震作用下相同路面粗糙度 (普通等级) 不同车速状况时车桥间竖向作用力随桥长的变化曲线。 可看出, 不同车速下车桥间竖向作用力波动幅度没有显著差别。

图4 车桥间竖向作用力随桥长变化曲线(车速60km/h, 路面粗糙度-好)
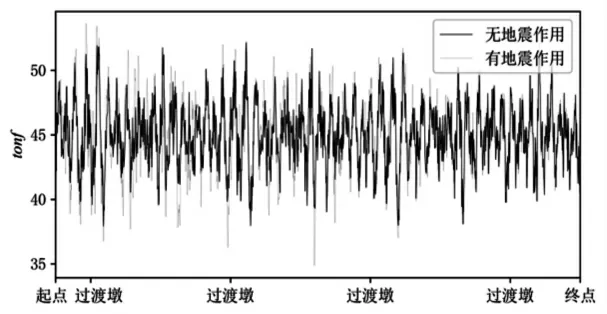
图5 车桥间竖向作用力随桥长变化曲线(车速60km/h, 路面粗糙度-普通)
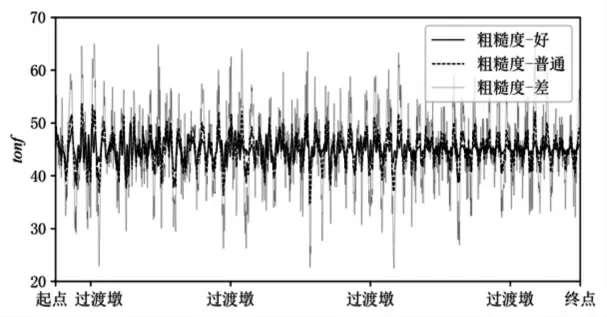
图6 车桥间竖向作用力随桥长变化曲线(车速60km/h)
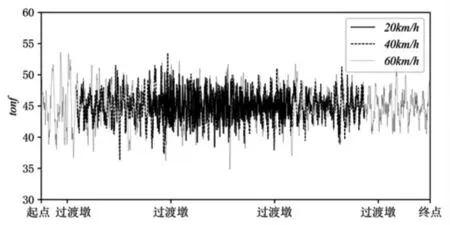
图7 车桥间竖向作用力随桥长变化曲线(路面粗糙度-普通)
2.4 车辆侧滑可能性分析
当车辆与路面保持横桥向位移一致所需要的作用力超过车辆与路面之间的侧向附着力极限(即滑动摩擦力) 时, 车辆将产生侧向滑动, 车辆方向难以控制, 正常行驶能力受到影响。 研究采用车辆侧向附着力需求系数进行分析, 并考虑干、 湿、 雪、 冰四种路面情况[5]。 车辆侧向附着力系数μlat,i(t)为t 时刻车辆所受侧向力作用力(t)与所受竖向作用力(t)的商, 即μlat,i(t)。 当μlat,i(t)>μa, 车辆发生侧滑,其中为路面滑动摩擦系数。 车辆侧向附着力需求系数即为车辆在通过目标桥梁过程中的车辆侧向附着力系数最大值。
图8 给出了车队在地震作用下通过目标桥梁的过程中在不同路面粗糙度不同车速状况时的车辆侧向附着力需求系数。 各工况下的车辆侧向附着力需求系数均大于雪和冰路面的滑动摩擦系数, 均小于干和湿路面的滑动摩擦系数。 说明典型车辆行驶在雪或冰路面遭遇突发常遇级地震作用时出现侧滑的概率极高, 而在干或湿的路面状况下出现侧滑的概率较低。 还可注意到, 路面粗糙度等级为‘好’ 和 ‘普通’ 时的车辆侧向附着力需求系数差别不大, 而路面粗糙度等级为‘差’ 时的系数值显著提高, 并呈现出随着车速增加而增加的趋势, 在60km/h 车速的情况下该系数趋近于湿路面的滑动摩擦系数, 有较高的侧滑风险。
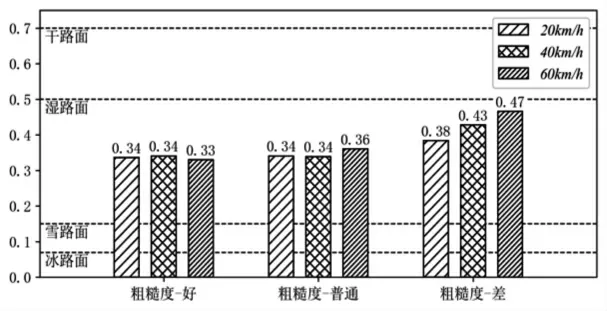
图8 车辆侧向附着力需求系数
2.5 车辆侧倾可能性分析
图9 给出了车队在地震作用下通过目标桥梁的过程中在不同路面粗糙度不同车速状况时的车辆侧倾系数。 各工况下的车辆侧倾系数都较高,均大于0.7。 在相同车速的条件下, 随着路面粗糙度的升高, 车辆侧倾系数均呈现出增大的趋势。 不过路面粗糙度等级为 ‘好’ 和 ‘普通’ 时的车辆侧倾系数差别不大。 而路面粗糙度等级为‘差’ 时的系数值显著提高, 并随着车速增加而增大, 在60km/h 车速的情况下该系数大于1.0,说明出现车辆侧倾的风险极高。
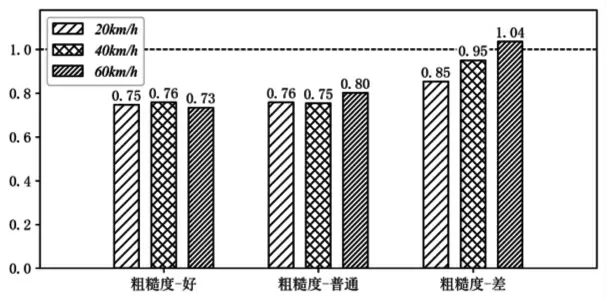
图9 车辆侧倾系数
3 结论
研究建立了一种求解地震-桥梁-汽车系统空间耦合振动问题的分析模型, 模拟了在突发地震作用下一列重车车队通过一座多跨连续梁桥的过程, 考虑了三种不同车速及三种不同路面粗糙度的情况, 分析了车辆在这个过程中出现侧滑或侧倾的可能性, 得到了以下一些结论。
(1) 地震作用下的车桥间竖向作用力的波动幅度会放大, 该放大效应与路面粗糙度相关。 相同车速下, 路面粗糙度越低, 波动幅度放大效应显著, 而路面粗糙度越高, 放大效应不显著。 而且车桥间竖向作用力的波动幅度与路面粗糙度的相关性较高, 而与车速大小的相关性较低。
(2) 车辆行驶在雪或冰路面遭遇突发常遇级地震作用时出现侧滑的概率极高, 而在干或湿的路面状况下出现侧滑的概率较低。 路面粗糙度等级为‘好’ 和‘普通’ 时的车辆侧向附着力需求系数差别不大。 而路面粗糙度等级为 ‘差’ 时的系数值显著提高, 并呈现出随着车速增加而增加的趋势, 在60km/h 车速的情况下车辆在湿路面的侧滑风险较大。
(3) 各工况下的车辆侧倾系数都较高。 在相同车速的条件下, 随着路面粗糙度的升高, 车辆侧倾系数均呈现出增大的趋势。 不过路面粗糙度等级为‘好’ 和 ‘普通’ 时的车辆侧倾系数差别不大。 而路面粗糙度等级为 ‘差’ 时的系数值显著提高, 并随着车速增加而增大, 在60km/h 车速的情况下出现车辆侧倾的风险极大。
因此, 从地震作用下的行车安全角度来讲,在运营使用中该桥梁的路面粗糙度等级保持在普通级别及以下的状况是比较好的, 并应及时除雪除冰。 此次研究未考虑桥梁结构长期变形等因素的影响, 如果考虑, 结果可能会更不利。

