基于距离和权重改进的K-means算法

王子龙，李 进，宋亚飞

1.空军工程大学 研究生院，西安 710051

2.空军工程大学 防空反导学院，西安 710051

1 引言

从海量数据中通过一定方法搜寻到隐藏于其中的信息的技术称为数据挖掘（Data Mining）技术[1]，在大数据、云计算高速发展的今天数据挖掘技术得到了广泛的应用。聚类是数据挖掘的一种方法，通过一定过程将数据集分为多个簇，簇内数据之间的相似度高，簇间数据之间的相似度低[2]。根据聚类手段的差异，聚类算法可分为划分聚类、层次聚类、基于密度的聚类、基于网格的聚类和基于模型的聚类[3]。

由MacQueen J[4]提出的K-means 算法是最广泛使用的聚类算法[5]，它是一种划分式聚类算法。经典K-means聚类算法具有一定的局限性，由于算法的初始聚类中心是随机设置的，聚类结果不稳定而且易陷入局部最优，结果易受噪声点影响；在聚类之前需要用户预先设定K值，算法的自适应性较差[6]。

近年来大量国内外学者在经典K-means算法的基础上对其进行了改进。Huang等人[7]提出了一种名为WKM（WeightedK-Means）的算法，给各个特征取不同的权重，用特征加权进行中心点的选择，综合考虑了不同维度数据对聚类结果的影响，但并未说明特征权重和特征值的尺度之间的关系。左进等人[8]提出依据数据的紧密性来排除数据集中离散点的影响，均匀选择初始聚类中心，但这种方法仍需手动确定K值。朱二周[9]等人提出了一种ZK-means 算法，初始聚类中心选的是数据集中密度较高的点，但后面未考虑噪点的影响。张素洁等人[10]根据样本集中的最远距离和样本密度来对中心点进行选取，然后综合SSE 值最终得出最优的K值，该算法获得了较高的聚类准确率，但时间复杂度较高。Zhang等人[11]提出了DCK-means算法，加入了Canopy的思想，同时在寻找初始点的过程中又结合了样本密度，在处理低密度区域时效果良好，但可能在聚类的过程中将离群点归为一个类，影响了聚类效果。钱雪忠等人[12]在密度峰值算法的基础上引入了K近邻思想来确定数据点的局部密度，然后提出了一种新的自适应聚合策略，有效提高了聚类准确度和质量，但是在此过程中引入了较高的时间复杂度，不适合在大型数据集上使用。王义武等人[13]运用空间投影的思想，将特征空间划分为聚类空间和噪声空间，并舍弃噪声空间，而聚类空间密度更高维度更小，使得算法时间消耗减小，但是当数据集特征维度高且稀疏时，算法可能找不到最优子空间。郭永坤[14]等人引入了高密度优先聚类的思想，提高了密度差异较大数据集的聚类效果，并且增强了算法的稳定性，但该方法未考虑孤立点存在的情况，而且在密度差异较小的数据集上的聚类效果一般。

针对上述部分改进K-means算法存在对噪点敏感、准确率不高以及时间消耗大的问题，本文以密度峰值算法思想为基础，并根据前人的研究经验，提出一种基于距离和权重改进的K-means算法，权重的计算综合了样本密度（Sample Density）、簇内平均距离（Mean Distance within the Cluster）和簇间距离（Distance between the Clusters），并且样本距离的计算采用的是加权的欧氏距离，加大了数据属性之间的区分程度，减少了异常点的影响，然后通过计算得到的样本密度、样本权值和距离来选择初始聚类中心，得到K-means聚类算法的初始输入参数，这个过程排除了孤立点的影响，有效解决了经典K-means 算法的抗噪性差以及易陷入局部最优的缺点，并且提高了算法的稳定性。在UCI数据集上测试实验结果表明，本文的改进K-means算法聚类准确度和效率更高。

2 改进K-means算法

2.1 经典K-means算法

经典K-means聚类算法的基本思想是：输入聚类数目k之后，首先从数据集中随机选取k个样本点作为初始聚类中心，然后计算各个样本点分别到k个初始聚类中心的距离，将样本按照距离最小原则归类，形成k个簇，再计算各个簇的平均值得到新的聚类中心，不断重复上述过程，直到聚类中心不再发生变化或者迭代次数达到设定的值之后，算法结束。

K-means 算法在计算样本之间距离时采用的一般是欧氏距离[15]，算法复杂度较小，适用于大型数据集，计算公式如下：

其中，xi={xi1,xi2,…,xim}和xj={xj1,xj2,…,xjm}为任意两个维度等于m的样本点，xip表示样本i对应第p个维度的具体取值。

2.2 基于距离和权重改进的K-means算法

2.2.1 相关概念

给定数据集D={x1,x2,…,xn}，其中的每个样本点可表示为xi={xi1,xi2,…,xim}，1 ≤i≤n，样本元素的维度为m。

定义1计算距离时样本点不同维度数据的权值[16]：

为了加大数据属性之间的区分程度，本文参考文献[16]中的权值计算公式来计算得到不同维度数据的权值。式（2）为维度权值计算公式。其中，xid是第i个样本数据中的第个分量值的大小；表示样本数据集中各个数据点的第d个分量的平均值，引入的权值在一定程度上能反应样本集整体的数据分布特征。

定义2维度加权后的欧氏距离如公式（3）所示：

式中,dw(xi,xj)是样本xi和样本xj在m维向量空间下维度加权后计算出来的的欧氏距离，后面简写为dwij，xid和xjd分别是在向量空间第d维下的样本点xi和样本点xj的数据值。

观察式（3），可以看出在引入属性权值之后，新的欧氏距离计算公式使得正常的数据与聚类中心的距离变小，而使得异常点与聚类中心的距离变大，从而减少异常点的影响，并且会使得原本不易区分的数据变得更为突出，起到了类似于放大差异的效果，有利于后面的聚类计算[16]。本文后面提到的样本之间的距离指的都是维度加权过的欧氏距离。

定义3数据集D的平均样本距离公式[11]为：

定义4数据集中样本点i的密度[17]为：

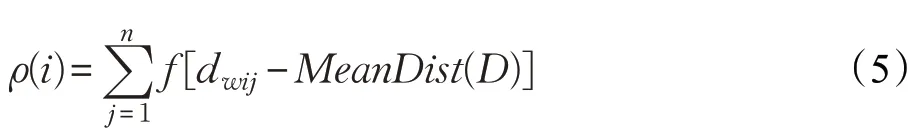
定义的样本密度直观解释如图1所示。

图1 样本点密度定义图解

定义5由定义4可知，ρ(i)的实际含义即为以样本点xi为圆心，以MeanDis(D)为半径的圆内包含的样本点的数目，将这些点归为一个类簇，它们之间的平均距离定义为：

定义6定义类簇之间的距离si，表示样本xi与另一个具有更高点密度的样本xj之间的距离。如果样本xi的密度不是最大，将si定义为min(dwij)，如果密度最大的样本点是xi，则将si定义为max(dwij)；数学表达式如下：

si的计算原则如图2所示。

图2 样本的簇间距离选择原则

定义7定义样本点xi的权重为：

由式（8）可以看出，ρi越大，即样本i周围点越密，则权重wi越大；si越大，即簇间距离大，则权重wi越大；ai越大，即簇内平均距离越大，一定程度上反映了簇内点样本分布比较松散，则权重wi越小。

定义8定义参数τi为：

其中，dw(xi,ci-1)是D中待选择样本点xi到上一个已选择的初始聚类中心ci-1的距离。由τi定义式可以看出，下一个待选择样本点到上一个中心点越远、权重越大，则参数τi越大，聚类中心就更可能在其附近产生，很好地反映了数据集D的全局分布特征，后面根据τi一步步选出来的初始聚类中心也减少了算法的迭代次数。

2.2.2 算法思想描述

算法思想为：首先由上面定义1 至定义7 计算出样本密度、样本权重，选择密度最大的点作为第一个聚类中心，这样可以有效避免孤立点、噪点的影响，然后计算当前聚类中心与数据集中所有点的距离，与它距离在MeanDist(D)之内的点不参加后面聚类中心的选择，然后将这个距离乘以相对应点的权重，即得到计算定义8中参数τi的值，选出其中的最大值，对应的点作为第二个初始聚类中心，然后删去距其MeanDist(D)之内的样本。重复上述过程直至数据集为空集，即得到k个初始聚类中心。

第一个聚类中心选的是密度最大的点，而后面聚类中心的选择依靠τi的值，由τi的定义式（8）、（9）可以看出，后面依次选出来的聚类中心都是密度较大，簇间距离大，簇内平均距离小的点，这就排除了像经典K-means 算法随机选择初始聚类中心那样选到噪点和孤立点的可能性，也符合密度峰值聚类算法[18（]Density Peaks Clustering algorithm，DPC）的假设：一个数据集的聚类中心由低局部密度的数据点包围，而这些低局部密度的点距其他高局部密度的点的距离较大。

初始点寻找过程如图3和图4所示。

图3 第二个聚类中心的寻找

图4 第三个聚类中心的寻找

2.2.3 算法流程

传统的K-means聚类算法需要手动输入聚类数目，并且初始聚类中心也是随机选取的，缺乏自适应性以及聚类结果的稳定性。本文通过以下步骤，可以自动确定初始聚类中心和聚类数目，具体步骤如下：

步骤1对于给定的数据集D，由公式（5）计算得到数据集内所有样本的密度，由公式（8）计算得到数据集D内所有样本元素的权重w。第一个初始聚类中心选择D中密度最大的对象c1，将之添加到聚类中心点的集合C中，此时C={c1}，然后将D中所有距离点c1小于MeanDist(D)的点删除。

步骤2选择具有最大τi=wi⋅dw(xi,c1)值的点xi作为第2 个初始聚类中心，记为c2，将c2添加到集合C中，此时C={c1,c2}，与第一步类似的，将D中所有距离c2小于MeanDist(D)的点删除。

步骤 3选择具有最大τi=wi′⋅dw(xi′,c2)值的点xt′作为第3 个初始聚类中心，记为c3，将c3添加到集合C中，此时C={c1,c2,c3} ，将D中所有距离c3小于MeanDist(D)的点删除，类似地不停重复上述过程，直到数据集D变为空集。此时C={c1,c2,…,ck}，由此得到k个初始聚类中心，即集合C中的样本点。

步骤4以上面步骤得到的初始聚类中心和聚类数为输入，对给定数据集D进行K-means 聚类运算，直到聚类中心不再变化。

步骤5输出最终聚类结果。

算法基于距离和权重改进的K-means算法

输入：Data setsD

输出：Clustering results

1.initialize the ArrayList；

2.computeMeanDist(D)；// 计算平均样本距离

3.FOR（each samplei∈D）{

4.computeρ(i)；//计算样本密度

5.}

6.FOR（each samplei∈D） {

7.computeai；

8.computesi；

9.computewi；//计算样本权重

10.}

11.select Centerc1←sample Maxρ(i)；

12.remove ClusterC1fromD；//找到第一个初始聚类中心并从D中删除该簇内所有点

13.WHILE（data setsD!=null）{

14.Centerci←sample（Maxτi）i；

15.remove ClusterCifromD；//从D中找到令式子wi⋅dw(xi,ci-1)最大化的点i作为下一个初始聚类中心，并删除该簇内所有点，不断重复直到数据集D为空

16.}

17.END WHILE；

18.PRINTF（K，Initial CenterC）；//输出得到K个初始聚类中心

19.K-means inpu（tD,K，Initial CenterC）；//将得到的初始中心点集合作为K-means算法的输入

20.WHILE（new center!=original center）{

21.FOR（each samplei∈D）{

22.FOR（each centercj∈C）{

23.computedw(xi,xk)；

24.}

25.IF（dw(xi,xk)=Mindw(xi,xj)）{

26.Centerck←samplei；//更新聚类中心点

27.}

28.}END FOR；

29.compute NEW Centerci=

30.Mean（sample（i&&（i∈Clusterci）））；

31.}END WHILE；

32.PRINTF（ClusterCi）；

改进后的K-means算法流程图如图5所示。

图5 基于距离和权重改进的K-means算法流程图

2.3 算法时间复杂度

理论上传统K-means算法的时间复杂度是O(nkT1)[19]，其中n为输入样本的个数，k是聚类数目，T1是算法聚类过程的迭代次数；WK-means算法引入了特征加权，时间复杂度是O(nm2l+nkT2)，其中m是样本维数，l是寻找初始点的迭代次数，T2是进行K-means聚类迭代的次数；ZK-means算法利用密度来确定初始聚类中心，而聚类过程和K-means 相同，其时间复杂度是O(n2kT3)；DCK-means 算法的时间复杂度为O(n2+nS+nkT4)，其中O(n2)是在计算密度的过程中引入的，S是寻找初始点的迭代次数，大小大约等于k；本文的改进K-means算法的时间复杂度是O(n2+nl+nkT5) ，O(nl) 是按步骤2 到步骤3 过程依次寻找初始聚类中心时引入的，l是初始中心点寻找过程中的迭代次数，数量级与k相当，T5是在输入初始聚类中心的前提下K-means 算法的迭代次数。在将本文提出的方法得到的初始聚类中心作为初始输入参数后，迭代次数T5将大大小于传统K-means 算法的迭代次数T1。这一点从后面实验部分的不同算法时间消耗对比可以看出。用本文的改进算法处理小中型数据时，在时耗上具有明显优势，当样本数量增大到一定程度时，本文的改进算法时间复杂度接近O(n2)。近几年提出的结合了密度的改进K-means算法的时间复杂度都在O(n2)和O(n3)之间[20]，由以上时间复杂度的理论分析可以看出，用本文的改进算法处理数据在时耗上更有优势，后面实验部分证实了这一点。

3 仿真实验

3.1 实验数据

本文仿真实验中采用的是UCI数据集，从其网站可以获得，UCI是加州大学提出的一个专门用来测试聚类效果的标准测试数据集[21]。本次实验，选用UCI的三个子数据集 Iris、Waveform 和 Glass，其中 Iris 数据集最简单，Waveform 和Glass 数据集结构相对更复杂，目的是为了更全面分析算法的有效性，数据集具体情况如表1所示，部分原始数据如图6所示。

表1 实验所用数据集的样本分布情况

图6 UCI数据集的部分数据示例

3.2 实验数据集的预处理

本次实验环境为：Intel®Core i7-8750H、16 GB内存、GTX1060显卡、Windows 10操作系统、Matlab R2016a。

原始数据在输入到算法之前必须经过数据预处理，一是因为原始数据不经过预处理一般情况下无法输入到算法中；二是即便可以顺利输入，若是给算法输入一个完全原始的数据集来测试，那么无论这个算法的理论准确率有多么高，实验结果也一般不会很理想；三是避免出现不同维度数据“大数吃小数”现象[22]，造成结果失真，因此，数据集的预处理工作是必不可少的。

3.2.1 数据集类别编号

Iris 数据集分为Iris-setosa（山鸢尾）、Iris-versicolor（变色鸢尾）、Iris-virginia（维吉尼亚鸢尾），原始数据集中它们的类别标号是英文单词，位于最后一列，为了便于实验，分别将三类数据编号为1、2、3。

Waveform数据集本身自有类别编号0、1、2，在这里为了统一改为1、2、3。

Glass 数据集原本类别编号为1、2、3、5、6、7（类别4的样本数目是0 个），在这里为了便于实验直接删除类别4，将编号重新设置为1、2、3、4、5、6，并删除作为数据序号标识的第一列数据。

3.2.2 数据标准化

式中，AVGp是所有的n个样本第p个属性的平均值，Sp是所有的n个样本第p个属性的平均绝对偏差，记xip′为标准化后样本xi的第p维度的值[23]。

3.2.3 数据归一化

数据经过标准化后，再将这些数值放到[0，1]区间[24]称为数据归一化，计算公式如下：

其中，xip″即为数据标准归一化后样本xi的第p维度的值，xpmin′为n个样本标准化后的第p维度数值最小的值，xpmax′为n个样本标准化后的第p维度数值最大的值。

3.3 聚类效果评价指标

大部分相关文献都将准确率[25]或者误分率作为聚类结果好坏的评价指标，所以本文也将准确率作为评价聚类算法优劣的指标，准确率的计算公式如下：

其中，是聚类结果中第i类样本的数目，Ci是第i类样本的真实数目。

除此之外，本文还加入了相对度量中的三种有效性评价指标对聚类效果好坏进行度量，分别为：

（1）分割系数PC[26]

PC的取值范围为[1/k,1]，值越接近于1，说明划分结果越清晰，聚类效果越好；反之，PC值接近1/k时，说明划分结果模糊。

（2）划分熵系数PE[27]

PE取值范围为[0,logak]，值越接近0，说明聚类效果越好；反之当PE值接近logak时，说明算法无法正确进行聚类。

（3）Xie-Beni指标[28]

本文选取的这三种聚类有效性评价指标很有代表性，现有的其他指标大部分都是这三种指标的变形。

3.4 实验结果与分析

本次实验，在UCI 的三个子数据集Iris、Waveform和 Glass 上对经典K-means 算法、WK-means 算法、ZK-means算法、DCK-means算法和本文算法进行测试和对比，每种算法分别运行50 次，结果取平均值。图7 为五种算法在实验数据集上的平均聚类准确率。

表2至表4是五种不同的算法在UCI数据集上的测试结果。

表2 算法在Iris数据集上的聚类结果指标

表3 算法在Waveform数据集上的聚类结果指标

表4 算法在Glass数据集上的聚类结果指标

3.4.1 聚类效果分析

从图7的准确率指标折线图可以直观看出，几种不同算法在Iris数据集上表现最好，在Glass数据集上表现最差，而两者数据集大小基本相同，可能原因是Glass数据集的类别数目和属性数目明显高于Iris 数据集的，Glass 不同类别的样本差异较小，数据分布分隔不是很明显。从表2 至表4 聚类结果四种指标的对比可以看出，本文提出的算法各项指标都是最优的，在三个UCI数据集上平均准确率比经典K-means算法高24.87%，比WK-means 算法高12.90%，比ZK-means 算法高7%，比DCK-means 算法高1.43%，总体上性能上接近但高于DCK-means算法，因为两种算法在寻找初始点的过程中都考虑了距离和密度，相比于其他算法更加具有全局性，而本文算法为了加大数据属性间的区分程度还引入了维度加权的欧氏距离，以及在初始聚类中心的寻找过程中引入参数τi，使得样本点之间的距离度量更准确，找到的初始点更能代表各类的大致分布，最终使得聚类结果更加优异。

3.4.2 改进算法的收敛性分析

当输入数据集一定时，改进K-means聚类算法的收敛速度和迭代次数主要取决于初始聚类中心的选取。

图8是本文算法和另外几种算法的聚类时耗对比，本文改进算法在3 个UCI 数据集上的时间消耗较其他四种算法有优势，与2.3 节中时间复杂度的理论分析基本一致。

图8 算法的平均时耗对比

表5显示的是算法的迭代次数，可以看出改进初始聚类中心的选择方法后，迭代次数均有所减少，其中本文改进算法的迭代次数要小于经典K-means算法、WK-means 算法、ZK-means 算法和 DCK-means 算法。根据文献[6]提出的初始聚类中心选择原理，聚类计算中用距离来度量数据对象之间的相似性，距离越小则相似性越高，对于密度不均匀的数据集，密度越高的部分越容易聚在一起，若能够找到k个分别代表相似程度高的那部分数据集合的聚类中心，那么将更加有利于算法收敛。本文的改进K-means 算法优化了初始聚类中心的选取过程，在密度峰值原理的基础上结合了数据集局部与宏观特征，并且采用加权距离减少了异常因素的影响，较其他改进算法考虑得更全面，选出来的初始点更符合上述初始聚类中心选择原理，从而减少了迭代次数，最终有利于减少运行时间。

表5 算法平均迭代次数

综上所述，本文提出的改进K-means算法的初始聚类中心选择方法较WK-means 算法、ZK-means 和DCK-means 的有优势，聚类结果的聚类精度更高且速度较快。从原理上看其优势在于：（1）采用维度加权的欧氏距离，减少了离群点的影响，增大了数据之间的区分度。（2）第一个聚类中心选的是密度最高的点，后面的聚类中心选择根据的是到上一个聚类中心的距离以及剩余点的权重，这个过程选出的点符合密度峰值原则，而噪点由于权重过小无法被选为聚类中心，避免了陷入局部最优。（3）由2.3 节时间复杂度的分析可知，理论时间复杂度相较其他改进算法较低。实验过程中还发现，测试传统K-means 算法时，对同一组输入数据，前后运行两次程序，输出的结果是不同的，而本文的改进算法在相同前提下多次实验输出结果稳定，这是因为传统K-means算法初始聚类中心是随机选取的，无法考虑整体情况，万一初始聚类中心选到离散点就会陷入局部最优解。而本文改进算法的每一步都是经过计算可以确定的，不存在随机性，初始聚类中心点的选择考虑了数据集整体的分布，结合了样本密度、权重和距离，因此排除了孤立点的影响，最终结果能够收敛到全局最优，避免了陷入局部最优解。

4 结束语

本文所提出的改进K-means算法，在聚类过程中结合了单个样本密度、样本的局部分布以及宏观分布，距离计算上还采用了维度加权的欧氏距离，解决了传统K-means算法的初始聚类中心选择问题，以及异常数据影响聚类效果的问题，并且时间性能也优于其他改进算法，最后的仿真实验结果表明本文改进后算法的各项性能指标更优，在聚类精度提高的情况下耗时也有所减少。聚类算法在数据爆炸时代应用广阔，根据前面理论分析，本文算法在处理中小型数据时由于明显减少了聚类过程中的迭代次数，比其他算法在速度上有优势，但在处理大型数据时由于寻找初始聚类中心引入了更高阶的时间复杂度，耗时将大于经典K-means 算法，这也是下一步需要解决的问题。