考虑旅客选择行为的节假日普速旅客列车编组优化研究
刘映宏,李海鹰,王 莹,王 佳
(1. 北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044;2. 北京交通大学 交通运输学院,北京 100044;3. 中国铁路济南局集团有限公司 青岛站,山东 青岛 266000)
截至2018年底,我国的铁路运营总里程已达13.1万 km,2018年全国铁路旅客发送量已达33.7亿人次,比上年增长9.4%。随着国民经济的发展和人们生活水平的提高,人们的出行需求也在日益增长,特别是在元旦、劳动节、端午节等小长假期间,越来越多的旅客选择铁路出行,客流激增导致很多车次出现“一票难求”的状态[1]。节假日期间铁路运力不足造成的客运瓶颈已成为铁路在运输企业市场化的激烈竞争中亟待解决的问题[2]。
对于普速旅客列车而言,为应对节假日高峰客流,铁路客运部门通常采用加开临客列车或加挂车底等方法,增加节假日期间普速旅客列车的运力。在实际运输组织中,加开临客列车会影响既有的列车运行图,增加调图工作,且根据以往客运组织情况,有些临时加开的列车存在上座率低等问题,易造成人力、物力、电力等资源的浪费,增加铁路旅客运输成本。此外,部分线路或区段能力接近饱和,致使加开列车的数量受限。因此,针对节假日客流,尤其是小长假期间的客流小高峰,在运行图既定的情况下加挂车底是较为理想的运力调节手段。
在申请普速旅客列车车底加挂时,通常由工作人员基于经验提出加挂方案并向路局提交申请,这种方式虽然简单易用,但受限于工作人员的个人经验,不具有连续性和稳定性,且缺乏科学依据,准确性较差。既有节假日旅客列车运行调整方面的研究主要针对节假日旅客列车开行方案优化[3-5]、动态客流下列车开行方案设计[6-7]、运行图调整[8-9]、节假日列车调度优化[10-11]等,涉及普速旅客列车加挂方案或编组优化的研究较少。在制定运输计划时,还应充分考虑旅客出行意愿,尽量满足旅客出行需求,而考虑旅客选择行为的普速旅客列车加挂方案或编组优化的研究更少。
在充分考虑旅客出行意愿的前提下,通过优化设计普速旅客列车加挂、甩挂方案,调整列车编组,利用有限的铁路设备设施资源来科学合理地组织运输生产,是目前亟待深入探索和解决的问题。本文结合随机效用理论,构建基于NL(Nested Logit)模型的旅客出行选择行为模型,分析旅客对于平行车次及席别的联合选择行为,并在此基础上,建立考虑旅客选择行为的节假日普速旅客列车编组优化模型,优化普速旅客列车的加挂方案,充分发掘普速旅客列车的运能潜力,力求以最小的运营成本满足最多的客运需求。
1 旅客出行选择行为模型
在优化旅客列车编组时,应充分考虑旅客的出行意愿,最大程度地满足旅客出行需求,本文基于NL模型研究旅客出行选择行为。对于同一运行区段内的普速旅客列车,各平行车次的运行时间相差不大且同一席别的票价基本相同,平行车次之间的差异主要是发车时刻不同,下面着重研究旅客对普速旅客列车发车时段和席别的联合选择行为。
1.1 NL模型结构
在NL模型中,旅客的出行决策可划分为两个层次,一层为列车发车时段选择肢,一层为席别选择肢。各层选择肢划分如下:
(1)列车发车时段选择肢:将一天划分为5个时段,分别为07:00—11:00、11:00—15:00、15:00—19:00、19:00—23:00、23:00—07:00。
(2)席别选择肢:普速旅客列车席别主要包括硬座、硬卧和软卧3种。
通过调查发现,旅客通常会优先选择列车发车时段,然后再选择席别。因此,构造列车发车时段位于上层、席别位于下层的NL模型,模型结构见图1。

图1 NL模型结构示意图
1.2 效用函数及选择概率
根据随机效用最大化理论,旅客选择出行方案的效用为
UTra=VTa+V(r|T)a+εTa+ε(r|T)a
(1)
式中:a为旅客;T为列车发车时段;r为席别;UTra为旅客a选择方案Tr的效用;VTa、εTa分别为旅客a选择列车发车时段T的效用函数中的固定项和随机项;V(r|T)a和ε(r|T)a分别为旅客a在选择T的情况下选择席别r的效用函数中的固定项和随机项。
当V(r|T)a和VTa与其所包含的解释变量之间呈线性关系时,可以表示为[12]
(2)
(3)
(4)
(5)

假定备选方案的效用误差项服从二重指数分布,则根据联合累积分布函数可知,旅客a选择方案Tr的概率Pa(Tr)为
Pa(Tr)=Pa(T)·Pa(r|T)
(6)
式中:Pa(T)为旅客a选择列车发车时段T的概率;Pa(r|T)为旅客a在选择T的情况下选择席别r的概率。二者的计算公式[12]为
(7)
(8)
(9)
式中:λ2为考虑上下层效用的概率项方差σ22所对应的参数,0<λ2/λ1≤1,当λ2=1时模型转变为MNL(Multinomial Logit Model)模型。
通过极大似然法对模型进行参数标定,可求得旅客对于普速旅客列车发车时段和席别的选择概率,从而得到旅客的乘车需求,为后续节假日旅客列车编组优化提供依据。
2 节假日旅客列车编组优化模型
本文研究的考虑旅客选择行为的节假日普速旅客列车编组优化问题,实际上是在既定运行图下,根据节假日期间旅客的出行需求和乘车意愿,优化普速旅客列车的加挂方案,调整列车编组,力求以最小的运营成本满足最多的客运需求。
2.1 相关条件假设
基于如下假设建立节假日旅客列车编组优化模型:
(1)由于节假日旅客列车的编组应尽量保持平日的编组结构,因此假设各列车的原有编组结构保持不变,可在原有编组的基础上加挂车底,但甩挂车底时不能改变原有编组。
(2)假设旅客列车在运行过程中是一个整体,只有在始发站才可以加挂车底,在终到站才可以甩挂车底。
(3)在实际运输组织中,旅客列车车底是配属于某个路局的,因此如果某列车在始发站加挂了车底,则假设其加挂的车底随原列车的车底交路返回始发站。
2.2 符号说明
集合、参数及变量符号说明如下。
(1)集合符号
Ω为所有列车的集合,列车i,j∈Ω;Φ为所有车站的集合,车站m,n∈Φ;Δ为所有车底类别(如硬座车、硬卧车、软卧车等),车底类别r∈Δ;Γ为所有列车发车时段的集合,时段T∈Γ。
(2)已知参数符号
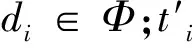
(3)变量符号

2.3 优化模型
面对节假日大幅增长的客流,铁路客运部门应在保持平日列车运行图结构的基础上尽量多加挂车底,尽可能地满足旅客的出行需求和乘车意愿,增加客票收入,同时节省铁路设备设施资源,避免资源浪费,以降低运营成本。因此,以运营成本最小化、客票收入最大化、旅客乘车需求满足率最大化为目标建立优化模型,模型为
(10)
(11)
(12)
s.t.
∀i∈Ω∀r∈Δ∀v∈Φ且oi≤v (13) ∀i∈Ω∀r∈Δ∀v∈Φ且oi≤v (14) ∀m∈Φ且oi≤m (15) ∀i∈Ω∀m∈Φ且oi≤m (16) ∀i∈Ω∀n∈Φ且oi (17) (18) (19) (20) (21) (22) θTr∈[0,1] (23) 上述模型为混合整数线性规划(MILP)模型,模型包括多个目标函数。对于多目标规划问题,应将多目标转化为单目标,再进行求解。 首先对各个目标函数进行归一化处理,具体处理方法为 (24) (25) (26) 式中:Zmax、Wmin、Wmax、Ymin、Ymax可以通过最小化或最大化目标函数求解得到,经过归一化处理后的目标函数值在区间[0,1]范围内。 然后,采用线性加权组合法,将归一化处理后的目标函数分别赋予一定的权重,并线性相加,从而将多个目标转化为单个目标。Z′和W′是站在铁路运输企业的角度,使其利润最大化,Y′是站在旅客的角度,使其出行需求和意愿得到满足。考虑到运输企业在制定运输计划时,既要保证运营收益最大,又要尽量满足旅客多样化的乘车需求,即寻求在尽量满足旅客的出行意愿和乘车需求的情况下,使运营企业成本最低、收入最高的旅客列车编组方案。因此将各个目标函数的权重均设为1,转化后的单目标函数为 maxI=-Z′+W′+Y′ (27) 经上述处理后,优化模型可直接通过ILOG CPLEX V12.3软件精确求解。 以某个3 d小长假期间途经某站的普速旅客列车为例,通过旅客出行选择NL模型,分析节假日期间旅客对于普速旅客列车的发车时段和席别的联合选择行为,确定选择概率,并以此为基础,结合第2节建立的旅客列车编组优化模型,对列车的加挂方案进行优化设计,并通过对比分析优化前后的加挂方案,验证模型的优化效果。 以小长假期间某日的实际客票数据(RP数据)为样本,对第1节构建的旅客出行选择行为NL模型进行标定,共获取8 533个有效样本。 影响旅客选择普速旅客列车发车时段和席别的因素主要包括出行距离、旅行时间、不同席别的票价、舒适度等,将这些变量带入到NL模型中,运用BIOGEME 2.6a软件通过极大似然法对NL模型的参数进行标定。经过多次运算,去掉t检验值低于1.95的变量,最终得出模型标定结果见表1。 由表1可知,NL模型的极大似然估计值L(β)为-16 428.142,调整后的R方(ρ2)为0.289,说明模型的拟合优度较高,模型能够很好地解释旅客的选择行为。 从标定结果可知,旅客的旅行时间越长,越倾向于选择卧铺。不同席别的票价对应的参数为负,而舒适度对应的参数为正,说明旅客倾向于选择票价更低、舒适度更高的席别,票价对应参数的绝对值比舒适度的大,说明旅客对票价更为敏感。 出行距离在800 km以内的旅客更倾向于选择硬座,800 km以上的旅客更倾向于选择卧铺。出行距离在400 km以内的旅客更倾向于选择07:00—19:00发车的列车;出行距离在400~800 km的旅客更倾向于选择07:00—15:00发车的列车或夕发(19:00—23:00发车)朝至列车;出行距离在800~1 200 km的旅客更倾向于乘坐夕发(15:00—23:00发车)朝至列车;对于出行距离大于1 200 km的旅客来说,23:00—07:00发车的列车不是其首选的乘车时段。 根据表1的计算结果,利用式(6)可计算得到每个出行者的选择概率,再借助Monte Carlo法[13]集计出每个备选方案Tr的选择概率PTr,计算结果见表2。 表1 NL模型属性变量及参数标定结果 表2 旅客对于列车的发车时段和席别的选择概率 根据历史客流数据和以往的客运组织情况,3 d小长假期间铁路客流量迅速增长,客流波动幅度较大,且小长假前后两天客流量均会出现较大波动,因此本文将研究的节假日时间范围定为7 d,包括节前2 d、节中3 d和节后2 d,并基于这7 d的实际数据,分别确定每日的旅客列车车底加挂方案。 本算例中共涉及普速旅客列车15对/d,共覆盖142个车站。各列车编有3类车底:硬座车底、硬卧车底、软卧车底。各类车底可容纳的客流量为车底定员量乘以可允许的超员率,因此硬座、硬卧和软卧车底的可容纳量分别为118×120%≈141人、66×100%=66人、36×100%=36人。加挂一节车底所带来的运营成本包括与运行距离有关的变动成本1.41元/(辆·km),以及不同类型车底的使用费:硬座车底2 800元/辆、硬卧车底4 200元/辆、软卧车底4 700元/辆。受车站到发线长度限制,各列车最多编组18节旅客车底。将各站的站存车底数设为很大的值以确定经济合理的加挂车底数,进而作为向路局申请车底的依据,若路局实际批复的车底数少于通过模型计算得到的车底需求量,则可根据实际可用车底数再次调用模型,给出车底约束下的最佳加挂方案。根据以往的客运组织情况,暂将超员率上限α定为120%,后续灵敏度分析中将集中讨论超员率上限α对加挂方案的影响,并确定经济合理的α值。 通过ILOG CPLEX V12.3软件求解模型,得到优化后的每日列车加挂方案,以及因加挂车底带来的运营成本、客票收入、旅客乘车需求满足率等情况,并将其与实际车底加挂情况进行对比,得到的结果见表3。 表3 优化前后的车底加挂方案对比 综上所述,优化后的加挂方案中,需加挂车底数量有所减少,运营成本大幅降低,客票收入略有减少,净收益比实际方案增加3.43万元,说明模型的优化效果较好。 为探求超员率上限α对加挂方案的影响,本文选取小长假第3天的客流数据,对普速旅客列车的加挂方案进行优化,通过调整模型中的α值,得到不同α下的车底加挂方案,具体结果见表4、图2。 表4 不同α下的车底加挂方案 α=100%表示只要分配到列车上的客流超过其可容纳量,就安排加挂车底,此时不会产生客流损失,总的客票收入最多,但由于存在即使超员很少也需要加挂车底的情况,这种方案下,需加挂的车底数量最多,因加挂车底带来的运营成本也是最高的。当α在100%~120%范围内时,随着α值的增加,需加挂的车底数量逐渐减少,运营成本逐渐降低,由于此时客流损失较少,客票收入略有降低,且降幅较缓,因此净收益逐渐增加。当α在120%~140%范围内时,随着α值的增加,需加挂的车底数量大大减少,运营成本降幅较大,但由于此时客流损失较多,客票收入也有较大降幅,因此净收益逐渐减少。综上,当超员率上限α的取值在120%左右时,运营企业的净收益是最大的。 图2 不同α对运营成本和客票收入的影响 节假日期间铁路客运需求激增,铁路运力十分紧张,在这种情况下,充分考虑旅客的出行需求和出行意愿,调整普速旅客列车的运输组织方案,充分发掘铁路运能潜力,是目前亟待深入探索和解决的问题,也是本文研究的重点所在。以往的研究着重关注的是节假日临客列车开行方案设计、运行图调整、列车调度优化等方面,而本文在充分考虑旅客出行意愿的前提下,重点关注旅客列车编组优化,通过优化设计普速旅客列车加挂方案,调整列车编组,充分发掘普速旅客列车的运能潜力,利用有限的铁路设备设施资源来科学合理地组织运输生产,为节假日期间铁路运力优化调整提供理论基础。 结合随机效用理论,构建旅客出行选择行为NL模型,分析旅客对于节假日普速旅客列车发车时段和席别的联合选择行为,从而获取旅客的出行需求和乘车意愿,并在此基础上,充分考虑旅客出行意愿,建立考虑旅客选择行为的节假日普速旅客列车编组优化模型,通过优化设计普速旅客列车加挂方案,调整列车编组,充分发掘普速旅客列车的运能潜力,力求以最小的运营成本满足最多的客运需求。经实例验证,与节假日期间旅客列车实际车底加挂情况相比,优化后的方案中,需加挂车底数量有所减少,因加挂车底带来的运营成本大幅降低,净收益比实际方案增加3.43万元,说明模型的优化效果较好。 在标定旅客出行选择行为NL模型时,主要以小长假期间某日的实际客票数据(RP数据)为样本进行标定,在进一步的研究中,可通过RP数据和SP数据相结合的方式,深入研究旅客的选择行为。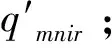
2.4 模型求解
3 算例分析
3.1 旅客出行选择行为分析
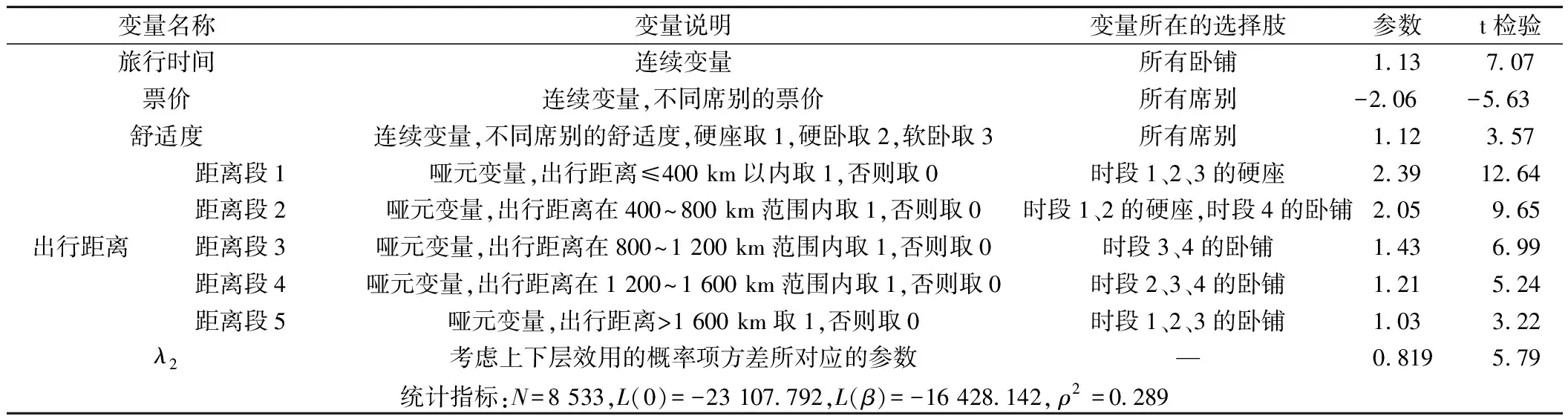

3.2 旅客列车编组优化结果
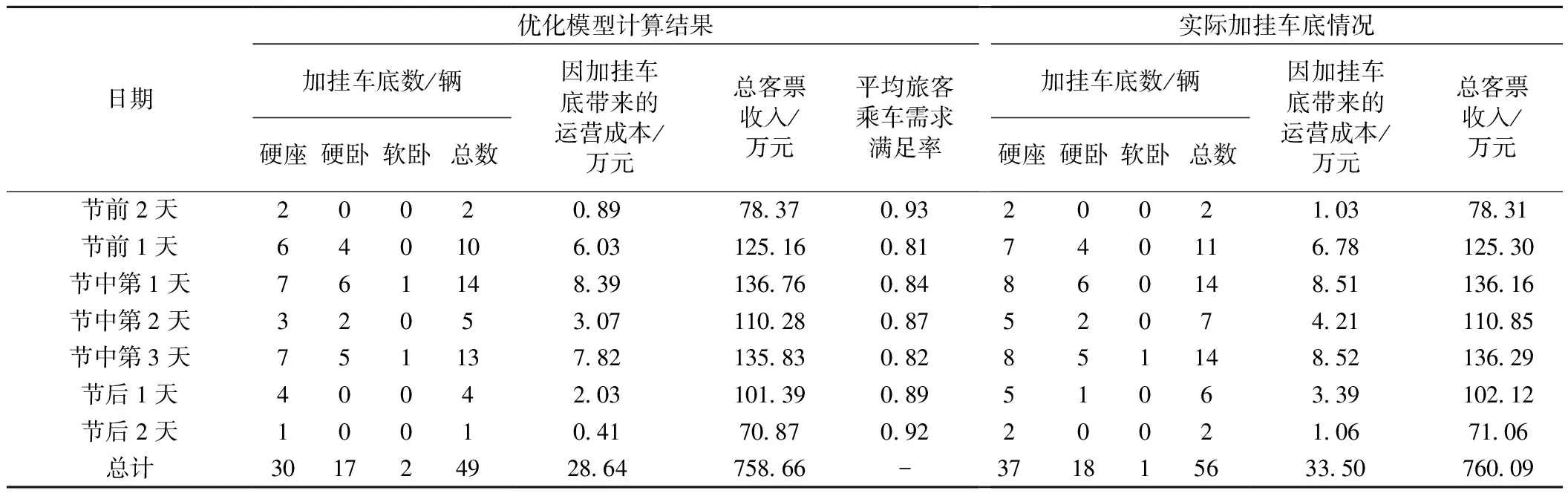
3.3 灵敏度分析


4 结束语

