基于自适应扩展卡尔曼滤波的消能减震结构及附加阻尼力识别
谢丽宇 李宪之 张睿 薛松涛

摘 要:针对消能减震结构中阻尼器提供的阻尼力难以直接测量,对其性能及状态进行评估较为困难的问题,提出了一种基于自适应扩展卡尔曼滤波的结构参数及未知激励识别方法,并将其应用于消能减震结构的阻尼器特性识别. 当阻尼器结构模型已知时,该方法可对阻尼器参数进行识别;当阻尼器结构模型未知时,阻尼器对结构提供的附加阻尼力可视为结构所受附加未知激励,同样也可由该方法进行识别. 采用一个多层剪切框架结构和一个多层加装阻尼器的消能减震结构作为数值算例,并采用一个单层加装阻尼器的剪切框架结构作为试验算例,验证了所提出的方法的有效性和可行性. 所提出方法可為消能减震结构中阻尼器的特性识别及性能评估提供更多的依据.
关键词:消能减震结构;附加阻尼力;扩展卡尔曼滤波;自适应
中图分类号:TU317 文献标志码:A
Identification of a Passively-controlled Energy Dissipation Structure and
Additional Damping Force Based on Adaptive Extended Kalman Filter
XIE Liyu1,LI Xianzhi1,ZHANG Rui1,XUE Songtao1,2?
(1. Department of Disaster Mitigation for Structures,Tongji University,Shanghai 200092,China;
2. Department of Architecture,Tohoku Institute of Technology,Sendai 982-8577,Japan)
Abstract:In order to solve the problems that it is difficult to directly measure the damping force provided by the damper of passive energy dissipation structure, and it is difficult to evaluate the performance and state of the damper, in this paper, a structural identification method based on adaptive extended Kalman filter is proposed and the method is applied to the damper characteristic identification of passive energy dissipation structures. Under the condition that the damper model is known, the damper parameters can be identified; under the condition that the damper model is unknown, the additional damping force provided by the damper can be considered as the unknown excitation and can also be identified by the proposed method. A multi-storey shear frame structure and a multi-storey damper controlled structure are used as numerical examples, and a single-storey damper controlled structure is used as experimental example to demonstrate the effectiveness and feasibility of the proposed method. The proposed method can provide more basis for the characteristic identification and performance evaluation of the dampers in the passive energy dissipation structure.
Key words:damper controlled structure;additional damping force;extended Kalman filters;adaptive
近年来,消能减震结构越来越多地应用在土木工程当中,为提高结构的抗震性能发挥了重要作用. 消能减震结构通常是在结构中安装阻尼器,由阻尼器吸收、耗散能量,增加结构的耗能能力,从而达到结构控制的目的. 阻尼器相当于结构的“保险丝”,其耗能能力对结构的抗震性能有着重要影响[1-3]. 然而,目前所采用的各类阻尼器在结构中的实际工作性能往往难以直接测定,阻尼器性能下降甚至阻尼器发生破坏都会给结构安全带来不良影响,如在2011年日本“3. 11”地震中,位于日本宫城县仙台市东北工业大学的某栋建筑出现了世界上首例油阻尼器震中破坏的现象[4-5]. 因此,对消能减震结构中阻尼器在实际工程中的工作性能进行研究有着十分重要的意义. 但是,消能减震结构中阻尼器的特性识别一直是一个具有挑战性的难题,阻尼器结构及作用机理的复杂性使得阻尼器对结构的阻尼力难以准确计算,而且在实际情况下阻尼器提供的阻尼力往往难以准确测量. 这就需要研究一种适用于消能减震结构阻尼器特性的识别方法,以对其模型参数或作用于主体结构的附加阻尼力进行识别[6-7].
卡尔曼滤波方法(KF)[8]是用于系统识别的一种有效算法,最早由Kalman提出,该方法可在部分观测结构响应的情况下对结构状态进行有效识别. 近年来有学者对其进行改进,提出了结构参数和结构状态同时识别的扩展卡尔曼滤波算法(EKF)[9-11], 此外还有用于结构参数、结构状态和未知激励同时识别的未知激励下扩展卡尔曼滤波算法(EKF-UI)[12-13]、用于强非线性结构识别的无迹卡尔曼滤波算法(UKF)[14]等. 但是这类滤波方法仍需要在一定的限制条件下才能实现良好的追踪和识别性能,如需要适当的初始条件、准确的参考模型和噪声分布的完整信息等. 然而,這类信息在实际工程中通常不准确或者不可知,这会导致卡尔曼滤波器性能下降甚至不稳定,使其难以直接用于消能减震结构的阻尼器特性识别.
基于此,本文采用一种改进的自适应扩展卡尔曼滤波方法,对消能减震结构的结构参数、阻尼器参数或附加阻尼力等进行识别. 对于消能减震结构,将其分为阻尼器模型已知与未知两种情况. 当阻尼器结构模型已知时,采用该方法对阻尼器结构参数进行识别;当阻尼器结构模型未知时,将阻尼器提供的阻尼力视为一种附加未知激励,并采用所提方法对该附加未知激励进行识别,即为阻尼器所提供的阻尼力[15]. 该方法采用实际情况下更容易得到的结构动力响应数据对消能减震结构的阻尼器特性进行识别,避免了直接测量结构所受附加阻尼力的困难,可以较好地识别阻尼器特性从而为阻尼器的设计和评估提供依据. 为了验证所提出方法的可行性,本文采用了一个多层剪切框架结构和一个加装阻尼器的多层消能减震结构作为数值算例,分别对其结构参数、阻尼器参数或附加阻尼力进行识别,并将其与理论值进行对比. 此外还设计一个单层加装阻尼器的剪切框架结构试验对该方法进行验证,从而说明所提出方法可有效应用于消能减震结构及附加阻尼力识别.
1 自适应扩展卡尔曼滤波方法
1. 1 扩展卡尔曼滤波方法
一个n自由度结构在外激励作用下运动方程为:
式中:M为结构质量矩阵;[x](t),[x] (t),x(t)分别为结构加速度、速度、位移向量;θ为结构参数向量;F [x(t),[x] (t),θ]是与结构参数及位移速度有关的力向量;f(t)为外激励向量.
当结构所受外激励已知时,将结构参数θ = (k1,k2,…,kn,c1,c2,…,cn)T扩展到结构状态向量Z(t) = {xT,[x] T,θT}T中,系统的状态方程和量测方程可写成:
式中:w(t)和v(t)代表模型误差与测量误差,假设其均值为零,协方差分别为Q(t)与R(t). 分别对状态方程和量测方程在Zk-1 = [Z][^]+
k处进行泰勒级数展开可得:
其中,相应的偏导矩阵表示为:
传统的扩展卡尔曼滤波方法主要有以下几个步骤,首先是状态预测:
k的误差协方差矩阵; Φ k-1≈I + Δt·G k-1为线性系统的状态转移矩阵.
接下来使用t = kΔt时刻的观测信息对预测值进行修正:
k为更新的协方差矩阵.
以上便是传统扩展卡尔曼滤波方法的主要步骤. 然而,传统的扩展卡尔曼滤波只能在先验知识准确的假设下才能实现良好的性能,包括参考模型、噪声分布和初始条件等.当先验知识不可用或不准确时,会导致该方法识别性能下降或不稳定[16].
1. 2 自适应扩展卡尔曼滤波方法
本文提出了一种具有时变遗忘因子的自适应扩展卡尔曼滤波方法,通过引入的时变遗忘因子λ对误差协方差矩阵[P][^] -
k进行修改[17-18],从而增大卡尔曼增益 K k,使更多的旧信息被遗忘,同时,该遗忘因子可不断调整,使其不至于过大或过小,算法可具有更好的识别能力和稳定性.
式中:Vk 为输出的误差协方差矩阵;ρ为衰减因子,本文中选取ρ = 0.95.
当结构所受到的外激励未知时,未知激励可由最小二乘法进行估计,相应的流程如下:
式中:[f][^]k为更新的未知外激励. 以上便是自适应扩展卡尔曼滤波算法的主要步骤.
2 数值算例及试验验证
为了验证本文所提出的自适应扩展卡尔曼滤波方法用于消能减震结构识别的有效性,设计两个数值算例和一个试验对其进行验证. 第一个算例为多层剪切框架结构,分别在外激励已知与外激励未知情况下对其进行识别. 第二个算例为加装阻尼器的多层消能减震结构,将其分为阻尼器模型已知与阻尼器模型未知两种情况,在阻尼器模型已知情况下对阻尼器参数进行识别,在阻尼器模型未知情况下对阻尼器提供的附加阻尼力进行识别. 试验设计为单层加装阻尼器的剪切框架结构,在阻尼器模型未知情况下对阻尼器提供的附加阻尼力进行识别.
2. 1 多层剪切框架算例
算例模型为5层剪切框架结构(见图1),结构参数为各层质量m1~5=300 kg,层间刚度k1~5=15 000 N/m,层间阻尼c1~5 = 100 N·s/m. 结构受EL-Centro地震波作用,选取50 s进行加载,采样时间间隔为0.02 s,地震激励的加速度峰值为0.2g = 1.96 m/s2. 在外激励信息已知情况下,仅观测结构第2、3、5层的加速度响应,并且该加速度响应信息包含2%的噪声. 识别结果如图2~图5所示.
由识别结果可知,对于剪切框架结构,在已知外激励情况下,自适应的扩展卡尔曼滤波方法可准确识别出结构的位移、速度等运动状态及结构的阻尼、刚度等参数. 此外该方法具有良好的抗噪性,在加噪2%情况下仍能对结构进行准确识别,而且仅需部分观测. 在未知外激励的情况下,该方法同样可对结构状态和结构参数进行准确识别,并且能识别出作用在结构上的未知外激励信息,因此,该方法可较好地用于结构系统及输入同时识别.
2. 2 多层消能减震结构算例
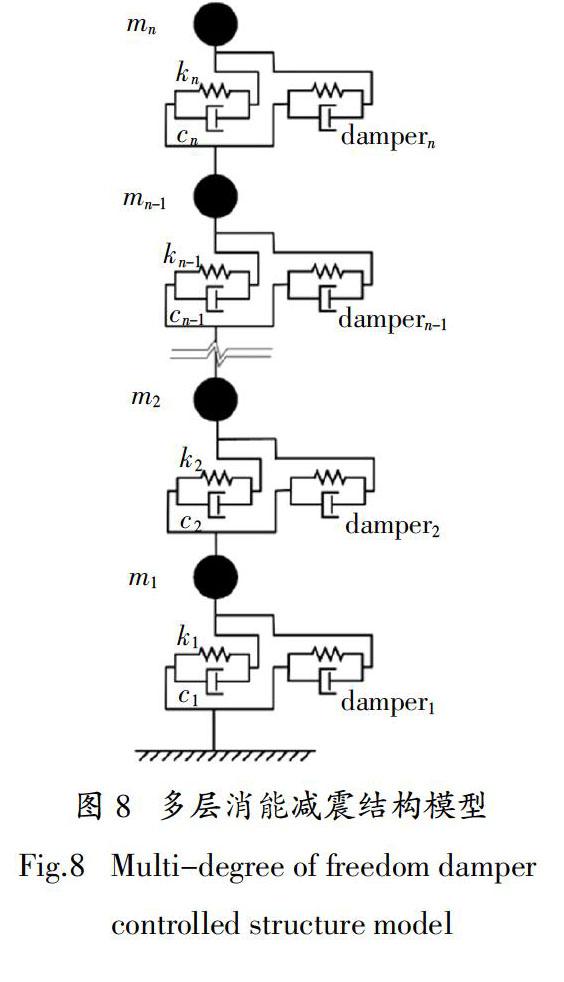
算例模型为一个加装阻尼器的5层消能减震结构,如图8所示,结构参数为各层质量m1~5 = 300 kg,层间刚度k1~5 = 15 000 N/m,层间阻尼c1~5 = 100 N·s/m. 阻尼器模型符合Bouc-Wen非线性滞回模型[19-20],表达式为:
式中:z为滞回位移分量;β,γ和n分别为Bouc-Wen模型非线性参数,本算例中选取β1~5 = 1 000、n1~5 = 2和γ1~5 = 1 000,阻尼器名义刚度为kd,1~5 = 5 000 N/m. 结构受EL-Centro地震波作用,选取 50 s进行加载,采样时间间隔为0.02 s.
在阻尼器模型已知情况下,观测结构的各层加速度及位移响应,对结构参数及阻尼器参数进行识别. 以第4层为例,识别结果如图9~图13所示.
在阻尼器模型未知情况下,阻尼器对结构提供的阻尼力可被视为作用于结构上的附加未知激励,该附加激励可由适用于未知激励情况下的自适应扩展卡尔曼滤波方法识别出来,即为阻尼器对结构所提供的阻尼力.相应的结构参数、结构状态及附加阻尼力识别结果如图14~图16所示. 结构参数及结构状态识别误差见表1.
通过识别附加阻尼力与理论阻尼器提供阻尼力进行对比,可以说明所提出的方法在阻尼器模型未知情况下可以有效识别出阻尼力,同时能够识别出结构的刚度、阻尼等结构参数,其中结构刚度的识别情况优于阻尼识别情况,最大误差不超过1%. 此外,对于结构位移、速度等结构状态,也可以进行准确识别.
2.3 试验验证
为了验证所提出方法的有效性与可行性,设计了单层带阻尼器的钢框架结构试验. 试验装置如图17所示,该单层钢框架高为1 m,楼板与柱均采用Q235钢板,楼板尺寸为834 mm × 390 mm,厚度为10 mm,柱尺寸为1 000 mm × 100 mm,厚度为3 mm,结构质量为23.0 kg.
试验测量装置主要包括3个部分:加速度传感器、激光位移传感器以及力传感器,布置位置如图17所示. 其中加速度传感器采用PCB333B30型加速度计,灵敏度100 mV/g,测量量程50g,频率范围0.5~3 kHz. 位移传感器采用基恩士IL300型激光位移传感器,测量量程为160 ~ 450 mm. 力传感器采用上海力恒LH-S09A微型拉压力传感器,量程为500 N,灵敏度为1.897 6 mV/N. 试验中,信号采样频率均为1 000 Hz.
对结构顶部施加80 mm初始位移,带阻尼器框架结构可进行自由振动,由加速度传感器与位移传感器可获得结构顶部加速度响应及位移响应,作为试验观测值.与结构相连的阻尼器为拉索式电涡流惯容阻尼器,其作用在主体结构上的附加阻尼力可由阻尼器与上部钢板相连的钢绞线上的力传感器测出. 对结构参数及在两种不同工况下的附加阻尼力的识别如图18~图21所示.
单层带阻尼器钢框架结构的试验结果表明,所提出的方法可有效识别出结构的刚度、阻尼等结构参数,并且识别出的阻尼器提供给结构的附加阻尼力与传感器实测结果符合较好,从而说明了所提出方法用于消能减震结构及附加阻尼力识别的可行性.
3 结 论
1)本文提出一种改进的自适应扩展卡尔曼滤波算法,可适用于外激励已知与外激励未知两种情况下的结构参数识别,而且在未知激励的情况下可对结构参数及未知激励同时进行识别.
2)将消能减震结构的识别分为阻尼器模型已知与未知两种情况,当阻尼器结构模型已知时,采用该方法对阻尼器结构参数进行识别;当阻尼器结构模型未知时,将阻尼器提供的阻尼力视为一种附加未知激励,并采用所提方法对该附加未知激励进行识别,即为阻尼器所提供的阻尼力.
3)该方法可有效用于消能减震结构的识别,通过实际情况下较容易得到的结构动力响应数据对阻尼器参数或阻尼器提供的阻尼力进行识别,可避免直接测量结构所受附加阻尼力,为阻尼器的设计和评估提供更多依据.
参考文献
[1] 林新阳,周福霖. 消能减震的基本原理和实际应用[J]. 世界地震工程,2002,18(3):48—51.
LIN X Y,ZHOU F L. Theory and application of energy dissipation seismic reduction technology [J]. World Earthquake Engineering,2002,18(3):48—51. (In Chinese)
[2] 謝丽宇,唐和生,薛松涛. 减振高层建筑的极限破坏及性能再生的研究现状及前景[J]. 结构工程师,2014(3):205—212.
XIE L Y,TANG H S,XUE S T. State-of-the-art and future trend in limit state and rehabilitation of vibration-controlled high-rise buildings [J]. Structural Engineers,2014(3):205—212. (In Chinese)
[3] 梅真,郭子雄. 磁流变阻尼器减振结构振动台试验与动力可靠性分析[J]. 湖南大学学报(自然科学版),2017,44(7):46—53.
MEI Z,GUO Z X. Shaking table test and dynamic reliability analysis of structures with MR dampers [J]. Journal of Hunan University (Natural Sciences),2017,44(7):46—53. (In Chinese)
[4] XIE L Y,CAO M,FUNAKI N,et al. Performance study of an eight-story steel building equipped with oil dampers damaged during the 2011 Great East Japan Earthquake Part 1:structural identification and damage reasoning [J]. Journal of Asian Architecture and Building Engineering,2015,14(1):181—188.
[5] CAO M,XIE L Y,TANG H S,et al. Performance study of an 8-story steel building equipped with oil damper damaged during the 2011 Great East Japan Earthquake Part 2:novel retrofit strategy[J]. Journal of Asian Architecture and Building Engineering,2016,15(2):303—310.
[6] MASRI S F,CAFFREY J P,CAUGHEY T K,et al. Identification of the state equation in complex non-linear systems [J]. International Journal of Non-linear Mechanics,2004,39(7):1111—1127.
[7] 宋琛琛,谢丽宇,薛松涛. 基于非线性阻尼系统解耦的消能减震结构系统识别[J]. 地震工程与工程振动,2015,35(5):161—166.
SONG C C,XIE L Y,XUE S T. System identification of energy dissipating structure based on decoupling nonlinear damping system [J]. Earthquake Engineering and Engineering Dynamics,2015,35(5):161—166. (In Chinese)
[8] KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering,1960,82(1):35—45.
[9] GHAHARI S F,ABAZARSA F,GHANNAD M A,et al. Response-only modal identification of structures using strong motion data [J]. Earthquake Engineering & Structural Dynamics,2013,42(8):1221—1242.
[10] 雷鹰,倪萍禾,刘朝. 有限观测绝对加速度响应下剪切框架在未知地震作用下损伤诊断[J]. 振动与冲击,2012,31(6):96—99.
LEI Y,NI P H,LIU C. Structural damage detection of a shear building under unknown earthquake excitation with limited observations of absolute acceleration responses[J]. Journal of Vibration and Shock,2012,31(6):96—99. (In Chinese)
[11] HOSHIYA M,SAITO E. Structural identification by extended Kalman filter[J]. Journal of Engineering Mechanics,1984,110:1757—1771.
[12] LIU L,SU Y,ZHU J,et al. Data fusion based EKF-UI for real-time simultaneous identification of structural systems and unknown external inputs[J]. Measurement,2016,88:456—467.
[13] YANG J N,LIN S,HUANG H,et al. An adaptive extended Kalman filter for structural damage identification[J]. Structural Control & Health Monitoring,2010,13(4):849—867.
[14] JULIER S J. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE,2004,92(3):401—422.
[15] 張睿,谢丽宇,薛松涛,等. 基于卡尔曼滤波的消能减震结构附加阻尼力识别[J]. 建筑结构,2018,48(S2):441—445.
ZHANG R,XIE L Y,XUE S T,et al. Kalman filter based structural additional damping force identification for damper controlled structures [J]. Building Structure,2018,48(S2):441—445. (In Chinese)
[16] YANG J N,LIN S. On-line identification of non-linear hysteretic structures using an adaptive tracking technique[J]. International Journal of Non-Linear Mechanics,2004,39(9):1481—1491.
[17] 穆騰飞,周丽. 输入未知条件下基于自适应广义卡尔曼滤波的结构损伤识别[J]. 振动工程学报,2014,27(6):827—834.
MU T F,ZHOU L. Structural damage identification using adaptive extended Kalman filter with unknown inputs [J]. Journal of Vibration Engineering,2014,27(6):827—834. (In Chinese)
[18] 张浩. 基于强跟踪无迹卡尔曼滤波的结构时变参数识别[D]. 兰州:兰州理工大学土木工程学院,2016:17—22.
ZHANG H. Structural time-varying parameter identification based on strong tracking unscented Kalman filter[D]. Lanzhou:College of Civil Engineering,Lanzhou University of Technology,2016:17—22. (In Chinese)
[19] WEN Y K. Methods of random vibration for inelastic structures [J]. Applied Mechanics Reviews,1989,42(2):39—52.
[20] 程骄阳,许斌,贺佳. 基于部分加速度测量的结构Bouc-Wen非线性恢复力及质量识别[J]. 噪声与振动控制,2018,38(2):179—187.
CHENG J Y,XU B,HE J. Identification of Bouc-Wen nonlinear restoring force and mass of structures with limited acceleration measurements [J]. Noise and Vibration Control,2018,38(2):179—187. (In Chinese)

