风廓线雷达数据精度评价与质量控制方法

左泉，鲍艳松，董焱，许丹，吴莹

(1.南京信息工程大学 气象灾害预报预警与评估协同创新中心，南京 210044；2.中国气象局气溶胶与云降水重点开放实验室，南京 210044；3.南京信息工程大学 大气物理学院，南京 210044)

0 引言

几十年来，对高空风的探测几乎都采用气球作为空气流动的示踪物。这种方式不能连续进行观测，时空分辨率低且费用较高[1]。风廓线雷达则是当前常规探空体制的重要补充[2]，每次观测时间只需几分钟，探测分辨率最小可到几十米，具有连续无人值守和全天候自动观测的优点[3]，可以连续获得测站上空的水平风速、垂直风速、大气折射率结构常数等信息[4-6]，是可以应用于业务的地基遥感设备[7]。

作为一种遥感探测设备，各种干扰信号都有可能使数据发生错误，其数据的质量问题也就更加突出[8]，尤其是在有降水情况下，水平风向、风速的测量误差相对较大[9-10]。风廓线雷达灵敏度高、波束较宽、副瓣较高，更易受到干扰信号的影响；而模式应用对风廓线雷达的数据质量也有很高的要求[11]。目前，我国在风廓线雷达硬件技术方面已比较成熟[12]，而在信号与数据处理及质量控制方面还有待提高[13]。为了获取一致性更高的探测资料并投入应用，研究切实可行的风廓线雷达数据质量控制方法是非常有价值且必要的[14]。

目前国内外针对风廓线雷达数据的质量控制开展过很多工作，也取得了一定的成果。美国NPN网和CAP网主要采用的是中值滤波算法、Weber-Wuertz 算法(WW算法)[15]和NIMA算法[16-17]。近十几年来，我国也有不少科学工作者和气象部门开始针对风廓线雷达数据的质量控制和资料应用展开研究。周芯玉等[18]利用中位数方法对广东阳江的风廓线雷达资料进行了质量控制和对比分析。文献[19-20]使用一致性平均方法、垂直一致性检测和中值检测等动态算法对山东省的风鄭线雷达数据进行了有效的实时质量控制。在风廓线雷达资料的同化应用方面，文献[21-23]利用风廓线雷达观测资料，把U和V联合起来进行EOF分解，利用分解出的主要模态重构该时间序列内的风场，使数据能更好地满足资料同化模式中的正态分布和无偏估计。其后，Zhang等[24]利用blacklisting对异常值进行检验，并用迭代重加权最小协方差行列式(IRMCD)法进行质量控制工作，推断IRMCD法在风廓线雷达数据质量控制中显得更有效且全面。另外，余贞寿等[25]在2018年通过对风廓线雷达资料进行气候极值检验、一致性检查、垂直稀疏化等质量控制，探讨了其在一次暴雨过程中对降水预报的影响。

由于风廓线雷达的观测受到多方面因素的影响，目前国内还未形成较成熟的针对不同地域风廓线雷达数据的质量控制方案。本研究主要针对北京地区7个站点的风廓线雷达数据展开研究，初步评价了数据的精度情况，并利用2种不同的质量控制流程处理数据，多方面比较不同的质量控制方法产生的效果及影响。

1 数据资料介绍

本文使用的观测资料来自北京7个站点(南郊、海淀、霞云岭、延庆、怀柔、平谷、密云)的风廓线雷达，时间分辨率均为6 min，空间分辨率为120 m。7台风廓线雷达的站点地理位置信息如表1所示。另外，用于评价风廓线雷达数据精度和数据的质量控制效果的风场数据来自美国气象环境预报中心(National Centers for Environmental Prediction,NCEP)和美国国家大气研究中心(National Center for Atmospheric Research,NCAR)联合制作得到的分辨率为0.5°×0.5°的FNL再分析资料。

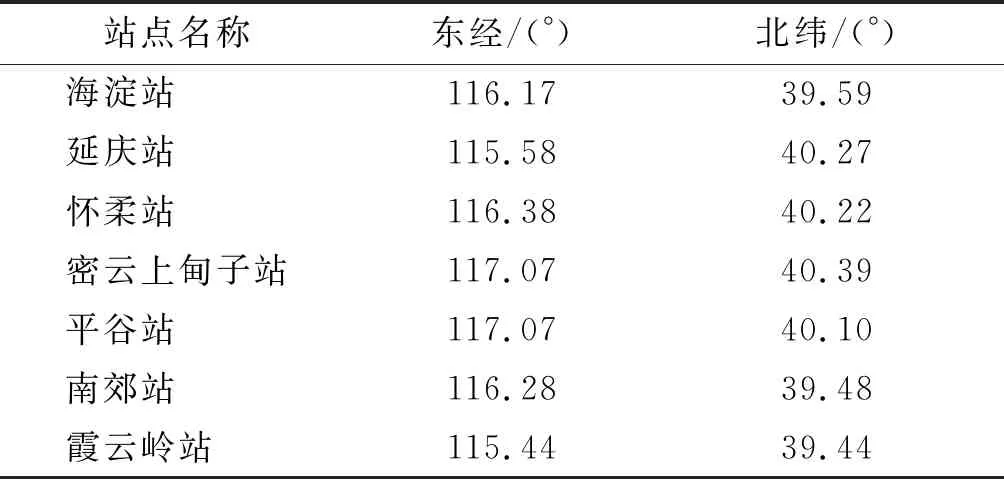
表1 北京风廓线雷达站点地理位置信息

2 风廓线雷达数据精度评价

2.1 数据精度评价方法

由于FNL再分析资料的风场为径向、纬向风分量(以下简称U、V分量)，故将风廓线雷达的水平风速根据风向分解成U、V2个分量。另外，由于2种数据资料的高度分层也不一致，所以在对比前先将风廓线雷达的风场数据插值到FNL再分析资料的高度层上，然后再进行对比分析，主要的对比技术流程如图1所示。

图1 风廓线雷达资料与FNL再分析资料对比流程

2.2 精度评价结果分析

选取了2018年6月当中7个站点均无地面降水的时段，并对风廓线雷达数据与再分析资料进行对比分析。从2018年6月各站点U、V分量散点图与相关系数及其一维线性拟合情况(图2、图3)来看，7个站点的散点分布与拟合情况大致相同，均有较强的相关性。其中，延庆站的U分量拟合情况最好，相关性也最强，而对于V分量来说，平谷站的相关系数最大，有较强的相关性。

注：红线为标准拟合线y=x，黑线为风廓线雷达资料与再分析资料的实际拟合线；R为相关系数。图2 2018年6月(无降水时段)各站点U分量散点对比

注：红线为标准拟合线y=x，黑线为风廓线雷达资料与再分析资料的实际拟合线；R为相关系数。图3 2018年6月(无降水时段)各站点V分量散点对比

另外，将FNL资料作为对比值，计算了各站点U、V分量各自的平均偏差和均方根误差，绘制出其随高度变化的垂直廓线，如图4所示。可以得出，密云站的总体误差较大，而南郊站的垂直廓线波动较小。在1 600 m以下，密云站的平均偏差绝对值是最大的，而平谷站相对较小且偏向稳定。到了高层，延庆、海淀、密云和霞云岭站的平均偏差绝对值开始不断增大，而南郊站的偏差绝对值则保持在1 m/s以内，且逐渐减小并趋于稳定。各站点的U分量从1 000 m开始向上，密云站的均方根误差始终是最大的，随着高度的上升，南郊站的均方根误差越来越小并逐渐趋于稳定。对于V分量来说，南郊和平谷站的平均偏差较小，绝对值基本维持在0～0.5 m/s，各站点均方根误差随高度变化差别不大，但密云站的误差相对来说还是比较大的，均方根误差最高已经超出了6 m/s。

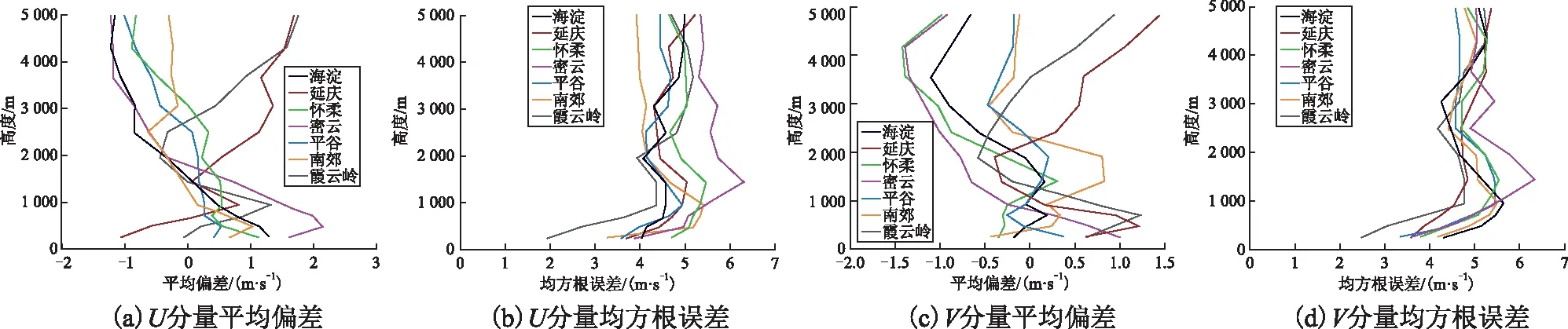
图4 2018年6月各站点U分量、V分量平均偏差与均方根误差垂直廓线

3 风廓线雷达数据的质量控制

3.1 质量控制前的数据检验

要对风廓线雷达观测资料进行质量控制，必须要考虑先对其进行质量检查。所以，针对原始的观测资料，本文首先进行了简单的气候极值检验[26]，用于剔除超过气象值最大限度的错误风场数据(表2)。

表2 风速气候极大值参考表

随后，又对极值检验后的风场数据进行了垂直一致性检验[27]。如果某高度层的垂直变化值同时大于其下2层的垂直变化值的3倍，则将该高度层上的水平风速看作异常风速值并予以剔除。由此，共计剔除了3.2%的水平风速异常值。

3.2 质量控制方案设计

1)EOF分析重构法。固定某一时次，选取该时次前1 h至后1 h的2 h内的数据构成时间序列，将U和V联合起来组成X矩阵[21]。计算X的协方差矩阵S=XXT，并求其特征值Λ与特征向量E(Λ为对角阵，对角元素即不同模态的特征值)。将特征值从大到小排列得λ1≥λ2≥…≥λ2L，计算前m个特征向量的累计解释方差如式(1)所示。

(1)

式中：L为数据的高度层。然后求时间系数矩阵T=ETX，利用EOF分解出的模态重构2 h内的时间序列，即X=ET，从而获得选取的分析时刻的风场垂直分布(针对累计解释方差设置了针对性截断阈值，设前m个特征向量满足G≥90%，且前m-1个特征向量不满足G≥90%，则重构时将只采用前m个模态的特征向量)，此时得到相应的第i高度层上第j时刻的径向风和纬向风分别如式(2)、式(3)所示。

(2)

(3)

式中：ei,k为特征向量E中的元素值；tk,j为时间系数矩阵T中的元素值。

2)高斯滤波法。高斯滤波是一种线性平滑滤波，本文也利用了二维高斯算子对研究数据的序列进行重加权，即利用高斯核的一维卷积算子对U、V风场的高频噪声进行过滤[28]。高斯分布如式(4)所示。

(4)

其中，σ越大，平滑效果越好。经过多次试验结果的比较，最终在本研究中取δ为1.5。

3.3 质量控制结果分析

针对2018年6月中的每一个地面无降水时段，本文对南郊站的风廓线雷达数据分别进行了上述2种方法的质量控制工作，并与FNL再分析资料进行对比，以比较2种质量控制方法的效果和作用。

1)时空尺度对比分析。图5为2018年6月6日6时(世界时，下同)U、V分量质量控制前后廓线对比图。可以看出，质量控制后的风廓线雷达数据显得更加平滑，数据一致性也更好，但2种质量控制方法的效果存在着较明显的区别。风廓线雷达初始风场在垂直方向上存在较大的波动，这一特征在U分量中尤为显著。在高度的变化上，经过EOF重构后的风场比高斯滤波场更加均匀，尤其是对于U分量(图5(a))，它滤去了很多在垂直方向上的大幅度风速变化，使得风随高度的变化变得平缓。而高斯滤波后的风场则与初始场较为接近，保留了很多初始风场的变化特征。

图5 2018年6月6日6时风廓线雷达U、V分量质量控制前后对比

为了进一步探讨2类质量控制方法在空间尺度上的定性影响特征，本文选取了另一时刻的风场垂直廓线进行了对比，图6为6月20日18时各风场的垂直廓线对比图。可以看出，在随高度变化的空间尺度上，高斯滤波场依然是更多地保留了风廓线雷达初始风场的变化特征，而EOF场则相对显得更加平滑和均匀，有效地过滤了相邻高度上风速的较大变化。因此，在很多强对流天气发生的情况下，高斯滤波法能够更多地保留风场在垂直方向上的较大切变。

在随时间演变方面，分析6月6日4时6分至7时54分风廓线雷达观测风场与质量控制后得到的风场在1 590 m高度上的时间序列后发现，质控后的风场相比原始风场要更加平缓(图7)。可以很明显地看出，无论是U分量还是V分量，高斯滤波后的风场都相对变得更加平滑，并且在滤去了某些小尺度高频脉动的同时，也相应地在一定程度上保留了初始风场在时间尺度上的变化特征，比EOF重构场更加接近于初始风场，从而能够有效地防止了部分情况下风场随时间演变的有效变化被当作异常值剔除的错误发生。

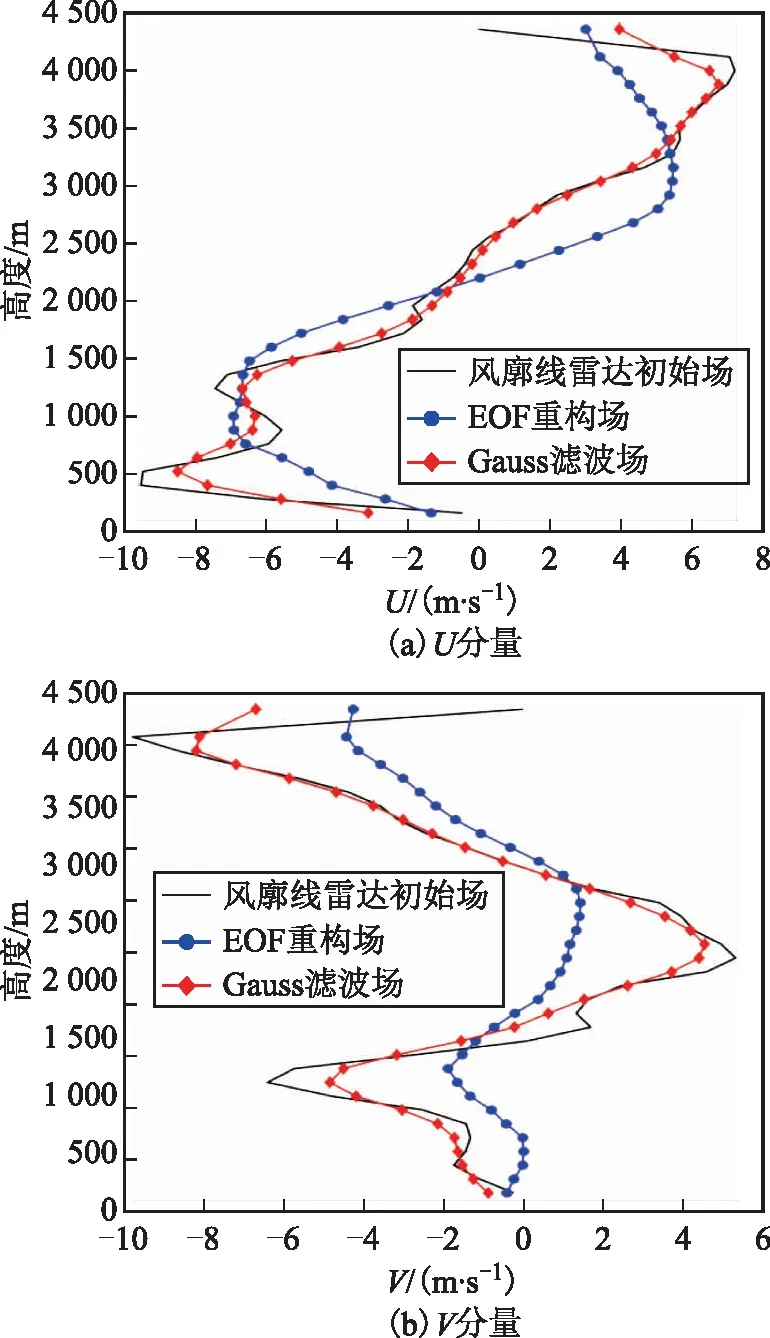
图6 2018年6月20日18时风廓线雷达U、V分量质量控制前后对比

图7 2018年6月6日4时6分至7时54分观测风场与质量控制风场在1 590 m高度上随时间的演变

随后，为了进一步验证上述2种质量控制方法的效果，本文给出了6月6日4时6分至7时54分风廓线雷达初始风场与质量控制后得到的2个风场的U、V分量随高度和时间的变化情况(图8)。与初始场进行对比分析可以发现，2种方法都可以滤去大部分的高频脉动，但高斯滤波法在去掉这些小尺度高频脉动的同时，也较好地保留了原风场的基本特征，很好地改善了这个时间段内风场的均一性。从图中还可以看出，高斯滤波法所得到的风场在时间尺度上更为均一，而EOF重构的风场在空间尺度上更为平均，这也与上述得出的结论相符合。因此可以认为，2种质量控制方法在时间和空间尺度上有着不同的效果。

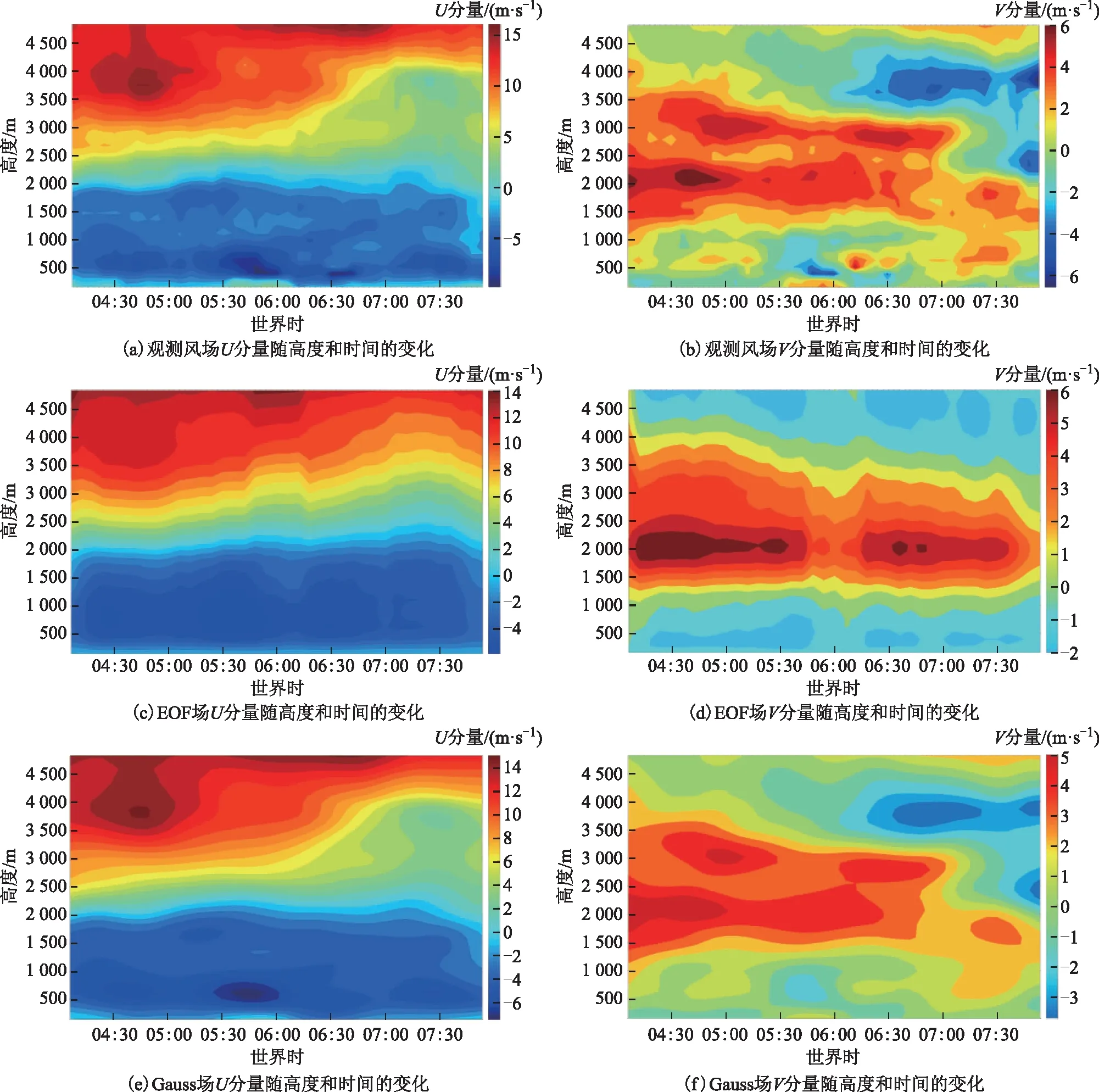
图8 2018年6月6日4时6分至7时54分观测风场与质量控制风场(EOF场、Gauss场)的U、V分量随高度和时间的变化

2)误差分析。由于在探空数据的观测过程中，存在时间分辨率过高、探空气球在水平方向上的漂移等实际因素，故本研究将FNL再分析资料的风场数据作为第三方观测数据，用于评价质量控制的效果。由于风廓线雷达的垂直分辨率较高，数据分布密集、高度层与FNL再分析资料差别较大，故针对风廓线雷达初始风场和质量控制后得到的风场进行了垂直稀疏化处理，即只取与FNL资料模式高度层相近的风场数据，以达到使其与再分析资料高度层数相同且垂直分辨率基本一致的目的。

对风场数据进行垂直稀疏化处理后，将其分别与FNL再分析场进行对比，计算并绘制出初始风场、2种质量控制场各自与再分析场差值的频数分布图(图9)。可以看出，各风场数据与FNL资料U分量的差值基本都集中在0 m/s附近，其中大多数差值分布在-2～2 m/s的范围内；而在差值为-0.4～1.2 m/s的区间内，2种质控场出现的频数比初始风场有所增多，尤其在0附近，Gauss场的频数相对于其他场，有较明显的提升，这在V分量的差值频数图中表现得更为显著。2种质控场在0～2 m/s的区间内频数增多，其中Gauss场在0.2～2 m/s的区间内，频数相比于EOF场和初始场都明显提高很多。但可能由于高斯滤波算法的原因，Gauss场的频数在差值极值区有略微的增加。

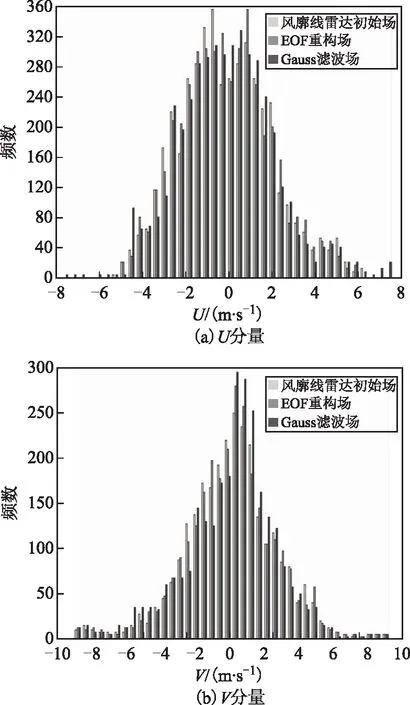
图9 2018年6月南郊站风廓线雷达初始场及质量控制场与FNL再分析资料风场差值的频数分布

由此，本文计算了各个风场数据与FNL再分析资料差值的平均值与标准差(表3、表4)。可以发现，2种质量控制方法得到的数据与再分析资料差值的平均值和标准差均比风廓线雷达初始风场要小，说明EOF重构法和高斯滤波法对改善数据偏差均有一定的作用。相对于EOF重构场，Gauss场与再分析场差值的平均值与标准差都更小一些，说明高斯滤波后得到的风场数据整体上更接近于FNL再分析场。

表3 风廓线初始场、质控场与FNL场U分量差值的平均值与标准差

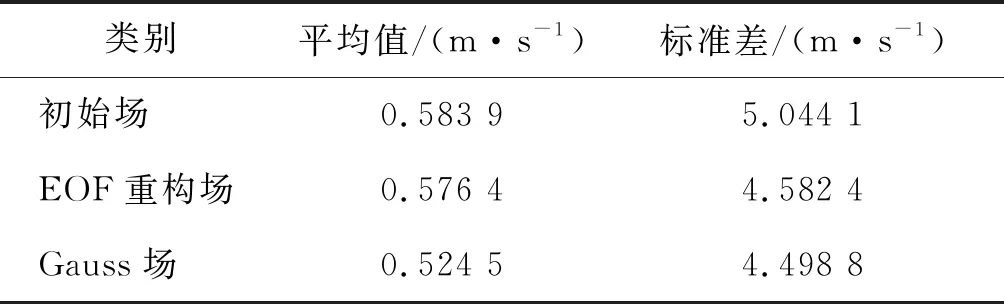
表4 风廓线初始场、质控场与FNL场V分量差值的平均值与标准差

4 结束语

本文选用2018年6月地面无降水时段北京南郊、海淀、霞云岭、延庆、怀柔、平谷、密云这7个站点的风廓线雷达的观测资料，将其与FNL再分析资料进行对比，得到初步的数据精度评估结果：7个站点上的U、V分量散点分布与拟合情况大致相同，均与再分析资料有较强的相关性，其中，延庆站的U分量拟合情况最好，相关性也最强，而对于V分量来说，平谷站的相关系数最大，有较强的相关性；从平均偏差和均方根误差二者结合来看，南郊站的误差相对较小，且数据的波动也比其他6个站点稳定。

随后本文对南郊站点的风廓线雷达数据进行了更加深入的研究。同样地，还是选取6月地面无降水时段南郊站所有时次的风廓线雷达资料，分别利用EOF分析重构法和高斯滤波法对其进行了质量控制，再将质量控制前后的数据与FNL再分析资料的风场数据进行对比，探寻这2种方法在时空尺度和误差分析上所产生的不同影响，得到主要结论如下。

1)在空间尺度上，EOF分析重构法的数据平滑效果更好，能够有效地过滤相邻高度上风速的较大变化，高斯滤波法得到的风场则是更多地保留了风廓线雷达初始风场的变化特征，在很多强对流天气发生的情况下，高斯滤波法能够更多地保留风场在垂直方向上产生的较大切变。

2)在时间尺度上，高斯滤波法的效果要明显优于EOF分析重构法。高斯滤波后的数据不仅随时间变得更加平滑，而且在滤去了小尺度高频脉动的同时，也相应地在某种程度上保留了初始风场在时间尺度上的变化特征，比EOF重构场更加接近于初始风场。

3)从风廓线雷达数据质量控制前后与FNL再分析资料的误差对比分析可以得出，2种质量控制方法在改善数据误差方面均能呈现出一定的效果，其中高斯滤波法相比于EOF重构法更能减小数据的观测误差。

需要指出的是，本文对质量控制方法在数据误差方面的影响展开了讨论，但没有更深入地研究质量控制前后风廓线雷达数据的实际技术应用，这在后期的工作中尚需进一步研究。