磁-腔量子电动力学系统中压缩驱动导致的两体与三体纠缠*

周英 谢双媛 许静平

1) (同济大学物理科学与工程学院， 先进微结构材料教育部重点实验室， 上海 200092)

2) (台州学院电子与信息工程学院， 台州 318000)

本文提出了一种通过压缩驱动放置一个YIG 小球的腔量子电动力学(QED)系统产生两体和三体纠缠的理论方案. 微波腔场与铁磁共振(FMR)模和静磁(MS)模的强耦合导致腔内光子、FMR 模和MS 模之间互相产生纠缠. 稳态情况下， 腔内光子、FMR 模和MS 模之间可以产生三体纠缠， 其三体纠缠的最小剩余共生纠缠度随非线性增益的增加而增大. 进一步研究发现， 该三体纠缠与MS 模式的耗散系数有关， 最小剩余共生纠缠随MS 模耗散系数的减小而增大. 同时还发现， 压缩驱动导致的三体纠缠对温度不敏感， 具有很好的鲁棒性. 结果表明磁-腔QED 系统是研究宏观量子现象的一个强有力平台.

1 引 言

强耦合与超强耦合是腔量子电动力学(cavity quantum electrodynamics， 腔QED)的研究热点，其可以在单粒子水平上研究光与粒子之间的相互作用[1]， 在量子信息科学、量子计量等方面具有广阔的应用前景[2-4]. 基于强耦合与超强耦合的腔QED 系统， 人们可以产生非经典光源[5，6]、超灵敏探测和控制[7]、超辐射现象[8，9]以及光子阻塞效应[10-12]等. 近年来， 钇铁石榴石(yttrium iron garnets， YIG)材料因出色的亚铁磁性质而备受关注.YIG 材料的居里温度为559 K， 因此， 其在低温[13-15]和室温[16]下皆呈现出铁磁性. 同时， YIG 材料不仅具有较高的自旋密度(约为2.1 × 1022cm—3)， 而且自旋之间存在较强的交换相互作用， 这使得集体自旋激发具有较低的耗散率(约为1 MHz). 已有研究表明， YIG 小球中波矢为零的Kittel 模[17]可与微波腔光子实现强耦合[13-16，18，19]和超强耦合[20，21]， 从而导致腔磁极化子. 由于腔内光子与YIG小球之间的强耦合使不同载体之间的信息传递成为可能， 故而促发了一系列有趣的研究， 例如： 双稳态[22]、腔自旋电子学[18，23]、磁暗态模[24]、以及磁诱导透明[25]等. 同时， 可磁控的慢光[26]以及Kittel模与单个超导比特(qubit)之间的耦合[27]也正在深入研究.

有关YIG 材料纠缠的研究是近几年一个重要的研究方向. Li 等[28]在放置一个YIG 小球的谐振腔磁力机械系统中， 由磁场直接驱动YIG 小球， 腔内光子和磁子通过磁偶极相互作用耦合， 磁子和声子则是通过磁致伸缩相互作用耦合. 在稳态情况下， 该系统实现了腔内光子、磁子和声子的三体纠缠. 同时， 他们还发现， 在腔中放置两个YIG 小球时， 也可利用YIG 小球内磁子和声子之间磁致伸缩提供的非线性作用， 实现两个YIG 小球内磁子间的纠缠[29]. 之后， Zhang 等[30]提出， 磁晶各向异性产生的Kerr 非线性作用可以替代YIG 小球因磁致伸缩而产生的非线性效应. 当采用蓝失谐的微波场驱动磁-腔QED 系统时， 可以实现两个相同YIG 小球内磁子间的纠缠. Nair 和Agarwal[31]则提出， 即使磁-腔QED 系统没有任何非线性， 采用压缩真空场[32，33]注入的方式， 同样可以产生非线性效应， 使两个相同的YIG 小球内磁子之间产生很大的纠缠.

本文考虑放置一个YIG 小球的磁-腔QED 系统， 以腔内光子、铁磁共振(ferromagnetic resonance， FMR)模和静磁(magnetostatic， MS)模作为研究对象， 采用泵浦光注入系统， 利用参量下转换使系统产生非线性， 从而使腔模压缩， 探讨产生纠缠的理论方案. 在该方案中， YIG 小球的集体自旋激发(FMR 模)， 及其频率附近的MS 模[19，34]同时与腔内光子产生强耦合. 通过光参量放大过程压缩驱动腔模， 使腔内光子、FMR 模和MS 模之间互相产生纠缠. 在一定的参数范围内， 它们还可以产生三体纠缠. 进一步研究发现， 纠缠的强弱与光参量放大的非线性增益系数和MS 模的耗散系数有关， 同时， 压缩驱动导致三体纠缠对温度不敏感，具有很好的鲁棒性.

2 理论模型

本文采用文献[19]的微波腔. 在微波腔中产生TE102模式， 为了使YIG 小球与微波腔场之间产生强耦合， 将YIG 小球放置在矩形微波腔短边(y方向)的中心处(如图1(a)所示). 这是因为TE102模式在这个位置具有较强的微波磁场， 且与微波腔短边平行. 同时， 外加一个x方向的静磁场， 则该静磁场与YIG 小球处的微波磁场垂直. 调节静磁场可使YIG 小球中的磁子与微波腔的TE102模式共振. YIG 小球内大量自旋的集体运动表现为铁磁共振模(FMR 模)， 在FMR 模共振频率附近还存在另一种集体自旋激发的模式， 即为静磁模(MS模)[19]. FMR 模和MS 模都是集体自旋激发的长波模式， 其中FMR 模是均匀磁化的Kittel 模[13-16]，而MS 模则是非均匀磁化模， 其磁化情况与样本尺寸有关.

根据腔量子电动力学理论， 该系统的哈密顿量可写为

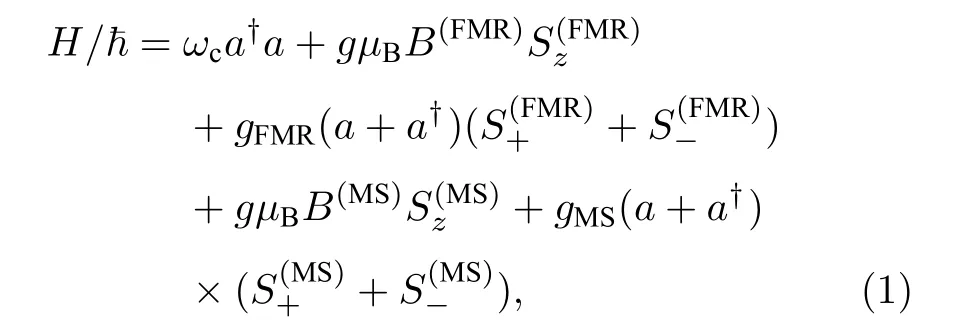
图1 (a) 磁-腔QED 系统示意图. YIG 小球位于腔中短边中心处， 该处微波腔的TE102 模式的磁场沿y 轴方向， 静磁场沿x 轴方向； (b) 利用Comsol 模拟微波腔TE102 的网格划分示意图； (c) 微波腔TE102 模式的磁场方向和磁场强度Fig. 1. (a) Schematic diagram of a magnetic-cavity QED system. A YIG sphere is located at the center of one short edge in the cavity， where magnetic field of microwave cavity mode TE102 is along y-axis direction， and static magnetic field is along x-axis direction； (b) schematic diagram of grid of microwave cavity mode TE102 by Comsol simulation； (c) magnetic field direction and magnetic field intensity of the microwave cavity mode TE102.

这里ωc表示腔模的频率，a(a†) 表示腔模中微波光子的湮灭(产生)算符，g为朗德g因子，µB为玻尔磁子，和B(MS)分别表示YIG 小球所处位置FMR 模和MS 模的有效磁场. FMR 模的集体自旋算符， MS模的集体自旋算符其中为FMR 模和MS 模的升降算符. 利用Holstein-Primakoff 变换[35]可以将磁子的集体自旋算符用磁子湮灭(产生)算符表示， 即

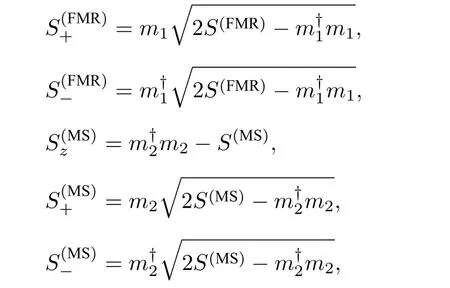
其中为FMR(MS)模的总自旋数，为FMR 模的湮灭(产生)算符，为MS 模的湮灭(产生)算符. 对于低激发情况，可以得到以 及令分别表示FMR 和MS模的角频率表示腔内光子与FMR(MS)模的耦合强度. 利用旋波近似， 哈密顿量(1)式可以写成

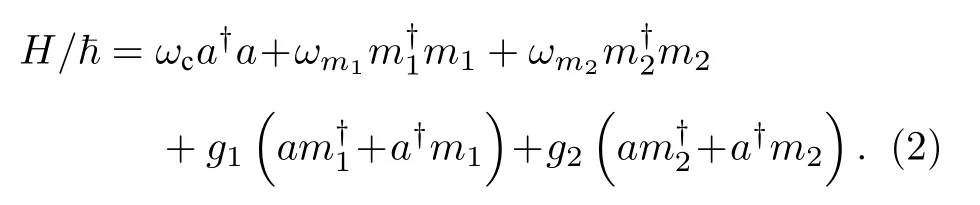
考虑一束角频率为ω0、拉比频率为εp的微波场沿x方向入射. 另一束角频率为 2ω0的泵浦场沿y方向驱动一块二阶非线性晶体， 利用二阶非线性过程产生压缩的腔模， 其光参量放大的非线性增益系数为Ω. 此时， 系统的总哈密顿量可写成

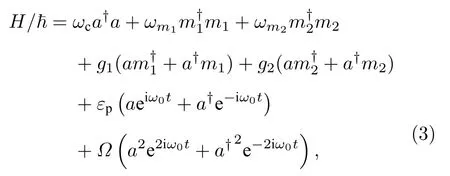
这里腔模中的光子、FMR 模和MS 模的湮灭(产 生)算符满 足对微波场频率ω0作旋转坐标变换， 系统的哈密顿量可简化为

其中，Δc=ωc−ω0为腔模的失谐量，Δm1=ωm1−ω0为FMR 模的失谐量，Δm2=ωm2−ω0为MS 模的失谐量.

根据量子朗之万方法， 可以得到一组算符的耦合方程组：

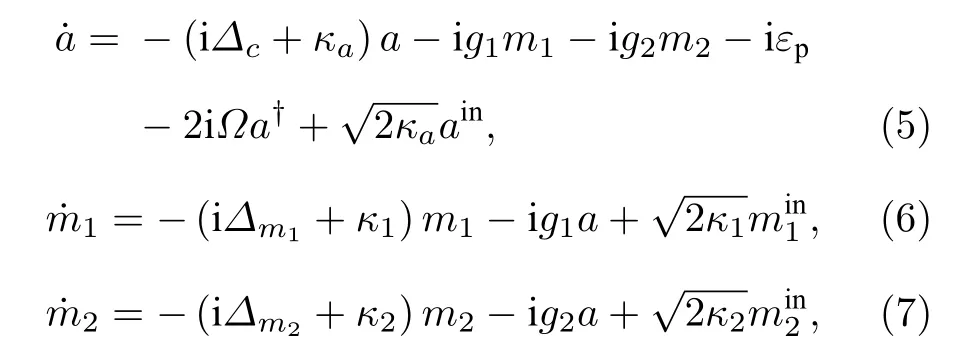
这里κa, κ1和κ2分别为微波腔、FMR 模和MS模的损耗，则表示输入的热噪声，其平均值为零， 并且具有如下关系[36]：

线性化方程组(5)式—(7)式， 即将算符写成O=〈O〉+δO(O=a,m1,m2)， 可以得到算符期望值的方程组：

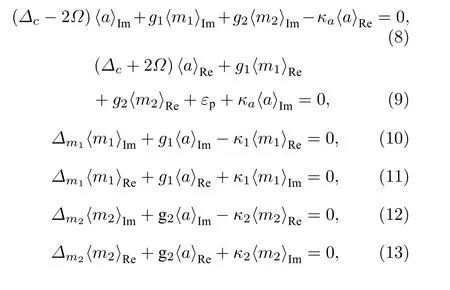
下标Re 表示实部， Im 表示虚部. 通过求解上述方程组， 可以得到稳态期望值如下：

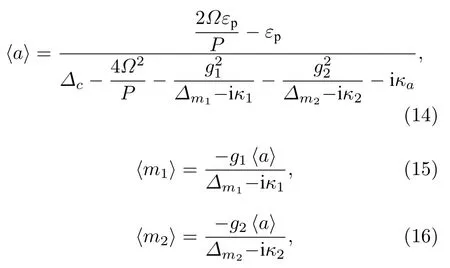
采用22 mK 时的实验参数[19]，=10.306 GHz，κa/2π=2.4 MHz，κ1/2π=1.3 MHz ，κ2/2π=3.3 MHz，g1/2π=7.5 MHz ，g2/2π=8.3 MHz ，ωm1/2π=10.306 GHz，ωm2/2π=10.265 GHz . 其中表明腔内光子 与FMR模和MS 模之间的耦合为强耦合. 对磁-腔QED 系统注入一束拉比频率εp=γ(γ/2π= 1.0 MHz) 的微波光场和另一束非线性增益Ω=1.5γ的泵浦光， 系统的平均光子数、FMR 模的平均磁子数和MS 模的平均磁子数如图2 所示. 显然， 在Δc≈0 ，Δm1≈20γ附近， 微波腔内平均光子数、FMR 模和MS 模的平均磁子数出现极大值， 其物理原因可以通过分析(14)式的极值点获得. 取P=0 且忽略所有耗散项， 可以得到(14)式的极值点位于Δc=0 ， 且当g1=g2，Δm1=−Δm2， 即Δm1≈(ωm1−ωm2)/2≈20γ时， 驱动场与磁-腔QED 系统的耦合最强， 从而可以观察到较多的光子数和磁子数.

3 磁-腔QED 系统中的两体纠缠

这里研究该系统中的两体纠缠. 忽略二阶涨落项， 腔内光子和两个磁模的正交涨落项可由下式给出：因此， 描述系统正交涨落项的线性朗之万方程(δX,δY,δx1,δy1,δx2,δy2)可以写成：

图2 (a) 平均光子数、(b) FMR 模的平均磁子数和 (c) MS模的平均磁子数随失谐量 Δ m1 和 Δ c 的变化关系， 其中γ/2π=1.0 MHz . 取 ε p =γ ， Ω =1.5γ ， 其他参数已在正文中给出Fig. 2. (a) Average photon number， (b) FMR mode average magnon number， and (c) MS mode average magnon number versus detunings Δ m1 and Δ c ， where， γ/2π=1.0 MHz . We take ε p =γ ， Ω =1.5γ . Other parameters are given in the text.

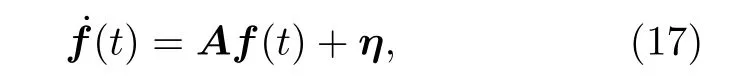
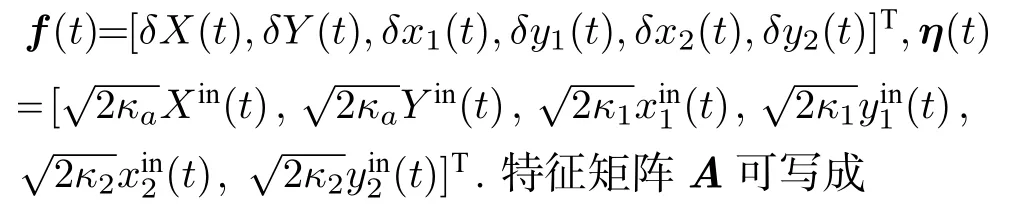
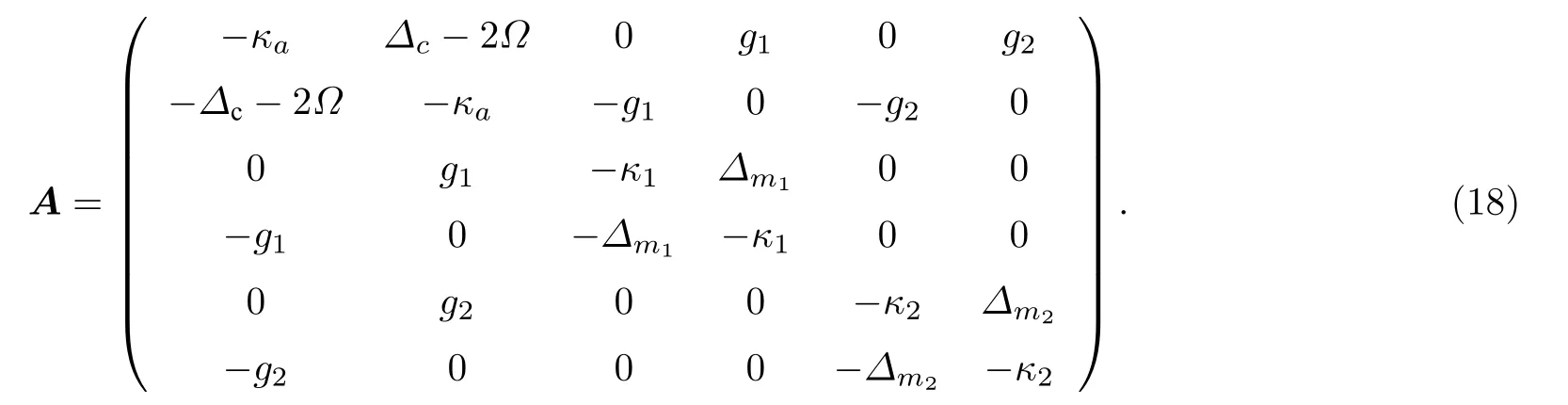
以高斯噪声为例， 系统量子涨落的稳态是连续变量的三模高斯态， 可以用6 × 6 的协方差矩阵V来描述， 定义为Vij=〈fi(t)fj(t′)+fj(t′)fi(t)〉/2(i,j=1,2,··· ,6).

一般地， 协方差矩阵V满足Lyapunov 方程[37，38]，即

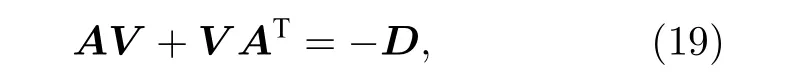
对于两体纠缠， 负值度EN[39，40]定义为

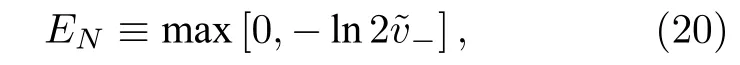
这里，为协方差矩阵的最小辛矩阵特征值，是辛矩阵，其中，P1|2=diag(1,−1,1,1) ，V4是三体系统中任意两体子系统的协方差矩阵.EN ＞0表示系统存在两体纠缠.

利用(20)式计算了腔内光子-FMR 模， 腔内光子-MS 模和FMR 模-MS 模之间的两体纠缠， 分别用Eam1，Eam2和Em1m2表示. 图3(a)—图3(c)分别表示Eam1，Eam2和Em1m2随失谐量Δm1和Δc的变化关系， 系统参数与图2 一致. 显然， 腔内光子、FRM 模和MS 模之间均产生两两纠缠(Eij始终大于零，i,j=a,m1,m2). 比较图3(a)和图3(b)可知，Eam1与Eam2几乎关于点(Δc≈0，Δm1≈20γ)对称. 当驱动光和FMR 模共振， 和MS 模非共振时(即Δm1=0 )， 光子和FMR 模的纠缠最大. 当驱动光和MS 模共振， 和FMR 模非共振时(即Δm1≈40γ)， 光子和MS 模的纠缠最大. 同时，Eam1的最大值略大于Eam2的最大值， 这是因为FMR 模的耗散系数略小于MS 模的耗散系数. 如图3(c)所示， 在Δc≈0，Δm1≈20γ附近， FMR 模-MS 模纠缠的负值度Em1m2出现极大值， 这是因为此时Δm1≈(ωm1−ωm2)/2≈20γ， FMR 模与MS 模具有相同的激发强度， 非线性效应最强， 从而导致该处负值度较大.

除了失谐量， 非线性增益系数也影响两体纠缠. 取Δm1=23γ，Δc=−2.5γ， 腔内光子、FMR模和MS 模之间的两体纠缠如图3(d)所示， 其中横坐标为非线性增益系数Ω. 当Ω=0 时(即只有线性驱动光)， 腔内光子、FMR 模和MS 模之间的两体纠缠度皆为零， 表明在没有非线性效应时， 系统不会产生两体纠缠. 利用参量下转换提供的非线性压缩驱动腔模产生纠缠， 这与利用压缩真空场[31]和磁晶各向异性的Kerr 材料[30]中的非线性产生纠缠的做法类似. 如图3(d)所示， 两体纠缠的负值度Eij随非线性增益系数Ω的增加而增大.

4 磁-腔QED 系统中的三体纠缠

最后， 考虑该磁-腔QED 系统的三体纠缠. 度量三体纠缠的最小剩余共生纠缠[41，42]满足：

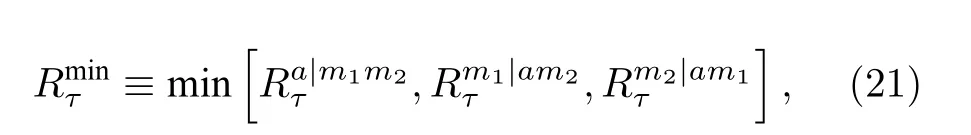
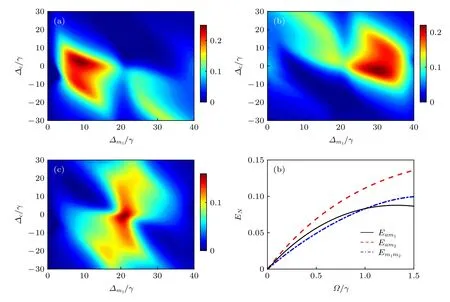
图3 两体纠缠的负值度 (a) E am1 ， (b) E am2 和(c) E m1m2 随失谐 量 Δ m1 和 Δ c 的变化关系. 其中 ε p =γ ， Ω =1.5γ . (d)负值度 E am1 (实线)、 E am2 (虚线)和 E m1m2 (点划线)随非线性增益 Ω 的变化. 其中 ε p =γ ， Δ c =−2.5γ ， Δ m1 =23γ . 其他参数与图2 一致Fig. 3. Density plot of logarithmic negativity related to bipartite entanglement (a) E am1 ， (b) E am2 and (c) E m1m2 versus detunings Δm1 and Δ c ， where ε p =γ ， Ω =1.5γ . (d) Logarithmic negativity E am1 (solid)， E am2 (dashed)， and E m1m2 (dot-dashed) versus the nonlinear gain coefficient Ω ， we take ε p =γ ， Δ c =−2.5γ and Δ m1 =23γ . The other parameters are the same as in Fig.2.

图4 (a) 不同非线性增益情况下， 三体纠缠的最小剩余共生纠缠 随失谐量 Δ m1 的变化关系； (b) 最小剩余共生纠缠随温度T 的变化， 其中 ε p =γ ， Δ c =−2.5γ . 虚线、实线、点线和点划线分别对应非线 性相互作用强度 Ω =1.65γ ， Ω =1.5γ ，Ω =1.0γ 和 Ω =0.5γ 的情况. 在图4(b)中， 取 Δ m1 =23γ ， 其他参数与图2 一致Fig. 4. (a) Tripartite entanglement in terms of the minimum residual contangle versus detuning Δ m1 ； (b) robust against temperature of the minimum residual contangle Where ε p =γ ， Δ c =−2.5γ . The dashed line， solid line， dotted line， and dash-dot line indicate nonlinear interaction strength Ω =1.65γ ， Ω =1.5γ ， Ω =1.0γ ， and Ω =0.5γ ， respectively. At the same time， we take Δ m1 =23γ for Fig. 4 (b). The other parameters are the same as in Fig. 2.

取Δc=−2.5γ， 图4(a)给出了三体纠缠的最小剩余共生纠缠随失谐量Δm1的变化关系. 显然， 当Ω=0 时，=0 ， 系统不存在三 体纠缠.当Ω＞0 时，＞0 ， 非线性效应导致系统出现三体纠缠， 且在Δm1≈20γ附近存在极大值，表示具有最强的三体纠缠度. 这是因为该处驱动场与磁-腔QED 系统的耦合最强， 非线性效应也最强， 从而激发了最大的三体纠缠. 随着非线性增益Ω的增加， 最小剩余共生纠缠的极大值也随之变大. 取Δm1=23γ， 图4(b)给出了三体纠缠随温度T的变化关系. 显然， 最小剩余共生纠缠对温度不敏感， 具有很好的鲁棒性. 同时发现， 非线性增益Ω越大， 三体纠缠的鲁棒性越好. 当Ω=1.5γ时，的温度鲁棒性可达到200 mK.同时还注意到， 在非线性增益系数Ω=0 时， 系统没有非线性， 所以没有纠缠. 当Ω＞0 时， 非线性效应导致三体纠缠的产生. 同时， 非线性导致的量子扰动和温度导致的量子扰动相互干涉， 从而导致图4(b)中出现一个小峰. 并且当T很小的时候，Ω导致的三体纠缠占主导， 当温度增大到一定程度后， 热扰动使三体纠缠度变小. 所以图4(b)中最小剩余共生纠缠随温度的变化不是单调减小， 并且在温度增大到一定程度后才出现显著下降.

除了非线性激发强度， MS 模的耗散系数也是影响三体纠缠的重要因素之一. 如图5 所示， 减小MS 模的耗散系数， 系统的最小剩余共生纠缠增大， 从而可以获得更大的三体纠缠.

图5 三体纠缠的最小剩余共生纠缠 随失谐量Δm1和耗散系数 κ 2的变化关系； 设定 ε p =γ ， Ω =1.5γ ，Δc =−2.5γ ， 从左到右， κ 2 所取的数值分别为 1 .7γ ， 2 .1γ ，2.5γ ， 2 .9γ 以及 3 .3γ . 其他参数与图2 一 致Fig. 5. Tripartite entanglement in terms of the minimum residual contangle versus detuning Δ m1 and dissipation rates κ 2 ， setting ε p =γ ， Ω =1.5γ and Δ c =−2.5γ ，the lines denote 1 .7γ ， 2 .1γ ， 2 .5γ ， 2 .9γ , and 3 .3γ forκ2 from left to right. The other parameters are the same as in Fig. 2.

5 结 论

本文提出一种利用新的非线性机制在磁-腔QED 系统中产生两体和三体纠缠的理论方案. 该磁-腔QED 系统中只含有一个YIG 小球， 腔内光子耦合YIG 小球中集体自旋激发的FMR 模和MS 模， 通过注入泵浦光， 利用参量下转换使系统产生非线性， 从而压缩驱动腔模， 使系统产生纠缠.采用实验可行的参数， 稳态情况下， 腔内光子、FMR模和MS 模之间互相实现两体纠缠. 当关闭泵浦光的输入(Ω=0 )， 系统不产生纠缠. 同时， 该稳态系统还可以实现三体纠缠， 度量三体纠缠的最小剩余共生纠缠随非线性增益的增加而增大. 进一步研究发现， 该三体纠缠与MS 模式的耗散系数有关， 减小MS 模的耗散系数， 系统的最小剩余共生纠缠增大， 从而可以获得更大的三体纠缠. 研究同时得出三体纠缠对温度不敏感， 具有很好的鲁棒性.

感谢同济大学朱成杰研究员、羊亚平教授和浙江大学李杰老师的有益讨论.