基于二氧化碳工质的回热器振荡流实验与模拟研究

陈 欣，肖 刚，童良怀，孙安苇，倪明江

（1.浙江大学能源工程学院，浙江 杭州 310027；2.衢州市特种设备检验中心，浙江 衢州 324002）

斯特林发动机（Stirling engine）因具有广泛的能源适用性且污染物排放易于控制，在余热利用、太阳能光热发电、水下动力等领域具有巨大的应用潜力[1]。作为一种闭式循环外燃机，长时间安全稳定地运行是评价斯特林发动机的重要指标。

氢气、氦气和二氧化碳均可作为斯特林发动机的循环工质。从安全性角度来说，氢气化学性质过于活泼，而斯特林发动机内部压力较大，采用氢气为循环工质时较为危险，不利于小型斯特林碟式系统的推广。从经济性角度来说，氢气和氦气获得成本较高，市面上的氢气和氦气价格分别是氮气和空气价格的4倍和35倍。从密封性角度来说，利用已有的100 W斯特林发动机进行各工质的密封测试，发现二氧化碳介质在斯特林发动机中的密封性能最好[2]。从效率角度来说，在转速较低时，使用二氧化碳作为工质的循环效率更高[3]。因此，在斯特林发动机中采用二氧化碳作为工质，适用于分布式热电联用系统，开发潜力巨大。

回热器是斯特林发动机的核心部件之一，其效率将对整机效率产生很大影响。倪明江等[4]采用改进型的Simple模型分析了100 Wβ型斯特林发动机，发现在研究工况下，回热器流阻损失占功率损失（功损）的20%，回热器导热损失占总能量损失的65%以上；Babaelahi和Sayyaadi[5]分析了GPU-3斯特林发动机内部的流阻损失，发现回热器的峰值压降是加热器和冷却器峰值压降和的8倍（频率41.67 Hz、压力4.14 MPa），并且换热器压降引起的功损占总功损的76.8%。已有一些学者针对常用的斯特林循环分析方法中计算流阻损失的关联式进行了研究，如表1所示。

表1 常用的斯特林循环分析方法中计算流阻损失的关联式Tab.1 The correlations for flow resistance loss calculation in common Stirling cycle analysis methods

表1中关联式主要是针对空气、氦气的流动特性，并未对二氧化碳进行相关研究。目前，二氧化碳工质在回热器中的流动特性尚不明确，无法利用相关分析方法设计和优化基于二氧化碳工质的斯特林发动机。

Peng等人[13-14]发现，在1个循环中，不同截面的质量流量不同。因此他们对各截面1个循环内的质量流量进行积分，得到工质的循环质量Mcr；再通过各截面的Mcr与理论循环质量Mct之比，提出循环率δ的概念。由此可以快速准确地计算出进入回热器的真实质量流量，以此设计效率更高、流阻更小的回热器。

为了开发二氧化碳工质斯特林发动机，提高回热器性能、机器效率和功率，完善斯特林循环分析方法，本文将针对二氧化碳气体在金属丝网回热器内部的流动特性开展系统研究，以获得气体循环率修正的定量方法，指导基于二氧化碳斯特林发动机的优化设计。

1 研究方法

1.1 研究思路

目前，对于回热器内气体工质振荡流的研究方法主要分为2种：一种是忽略金属丝网的实际结构，借助多孔介质模型简化计算过程，该方法依赖2个阻力系数，精度较差，且无法获得真实流场细节；另一种是在计算域中直接考虑金属丝网的实际结构，采用基于精细网格的有限体积方法（FVM）直接计算获得接近真实结构的流场细节。

本文采用有限体积方法，建立考虑实际金属丝网细节结构的CFD模型，计算二氧化碳与金属丝网的摩擦系数。然后，搭建回热器振荡流实验台，并建立完全相同的回热器振荡流模型（采用Fluent多孔介质模型），比较压降、压力结果，验证模拟的准确性。最后，对二氧化碳循环率进行研究。研究思路如图1所示。

图1 本文研究思路Fig.1 The research idea of this paper

1.2 几何模型和边界条件

建立模型，采用一类结构2层、二类结构3层的方式，交错堆叠，每层是横纵3条缠绕金属丝。20、100、200、400目丝网丝径分别为1、0.1、0.03、0.015 mm，孔隙率分别为0.85、0.65、0.63、0.53。流域总长是4倍丝网长度，两侧各1.5倍。Costa[10]、赖华盛[15]等人已经验证了5层丝网的准确性。图2是200目丝网的最终模型。为了更为准确地监测气体经过丝网后的温度、速度、压力等变化并反映气体与丝网的流动和换热过程的瞬时变化，在离丝网实体0.5倍丝径距离处建立了监测面1和监测面2（见图2d)）。

图2 金属丝网结构Fig.2 The structure of the wire mesh

内部气体的密度、黏度、热导率和比热容通过REFPROP软件进行拟合。入口采用速度入口，出口采用压力出口，金属丝网实体壁面采用耦合壁面，流域壁面采用对称壁面。时间步长通过频率计算得到，经过时间步长、网格无关性验证后取以曲轴转过1°为1个时间步长。网格数目为200万，网格质量大于0.5[15]。模拟工况见表2。

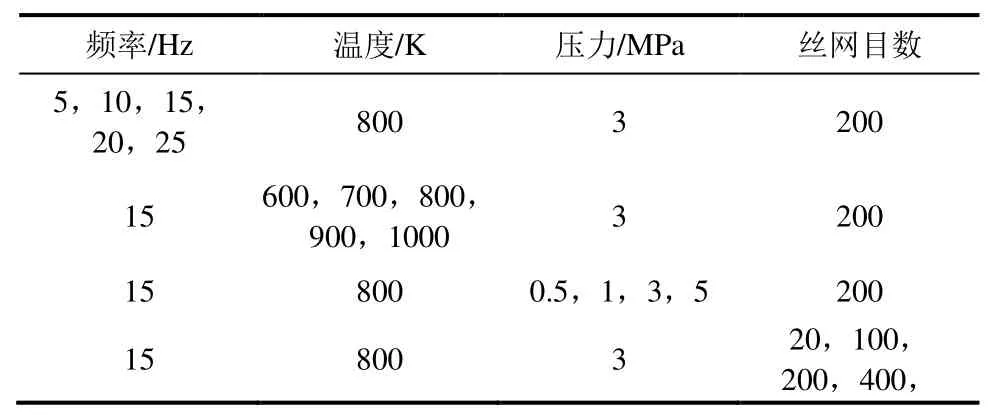
表2 二氧化碳工质模拟工况Tab.2 The simulation working conditions for CO2

1.3 数学模型

由于金属丝网内部特征流通直径较小，需要验算是否满足流体连续性假设。金属丝网参数见表3。

表3 金属丝网参数Tab.3 The structural parameters of the wire mesh

气体分子平均自由程计算公式如下[16-17]：

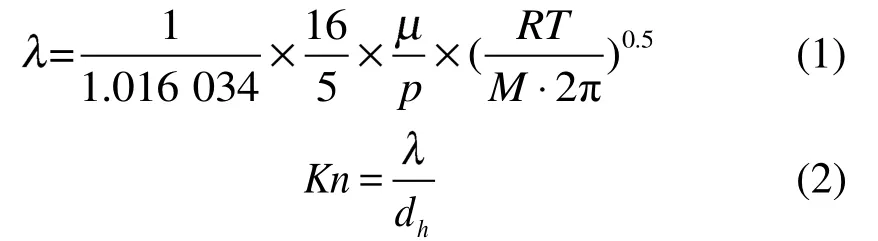
计算3个工况点（200目、0.5 MPa、800 K，200目、3 MPa、1 000 K和400目、3 MPa、800 K），分别得到。

由于克努森数Kn均小于0.01，因此在CFD模拟时可以采用连续性介质假设。

Fluent多孔介质模型中引入了2个参数（黏性阻力系数张量和惯性阻力系数张量）来描述动量方程（见式(3)），而回热器是各向异性的，只考虑轴向流动，源项可以表示为式(4)。

式中：S为源项；Cf为黏性阻力系数张量，m2；Cj为惯性阻力系数张量，1/m；A、B、C为拟合系数；孔隙率；Redh为雷诺数；dh为特征长度，m；p为压力，Pa；t为时间，s；为剪切应力，N。

目前，常用的流阻系数关联式拟合式如式(8)、式(9)。2种形式的拟合公式均来自Ergun公式：当C很小时，在低雷诺数下A/Re占主导；但在高雷诺数下，B/ReC的存在使得f更为准确。因此，本文采用式(9)。

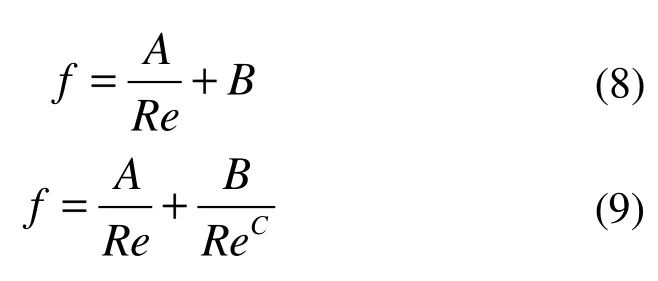
2 振荡流实验

2.1 实验准备

为了验证基于FVM的CFD方法得到的关联式的准确性，并对二氧化碳循环率进行研究，搭建了图3所示的振荡流实验台，其主要结构和仪器参数以及实验工况分别见表4和表5。

图3 实验台示意Fig.3 Schematic diagram of the experimental bench

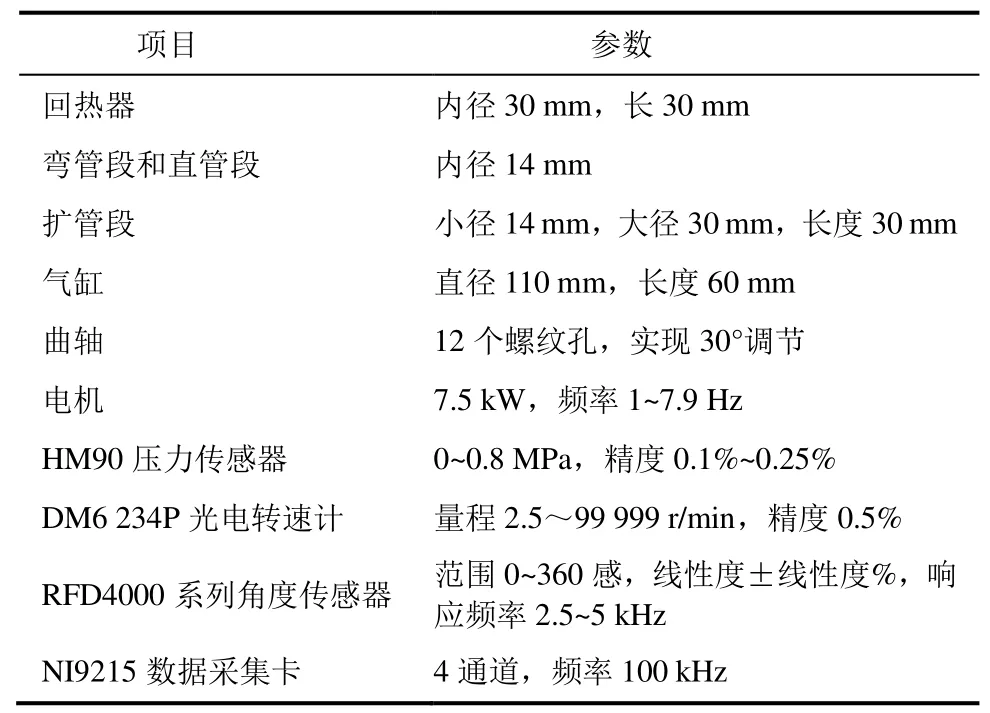
表4 实验台主要结构和仪器参数Tab.4 The main structural and instrumental parameters of the test bench

表5 实验台模拟和实验工况Tab.5 The simulation and experimental working conditions for test bench

进行实验前：先打开气瓶的阀门和所有管路阀门，对整个装置进行吹气；30 s后，关闭装置放气阀门，使装置充气（空气或二氧化碳）至0.6 MPa，静置5 min；打开阀门降压到0.2 MPa，启动电机30 s，使内部气体混合；再次充压至0.6 MPa。如此反复3次，保证内部工质气体的纯度。此外，在前期的测漏实验中发现，在装置充压至0.6 MPa时，40 min后压力下降了0.02 MPa。为了解决密封性的影响，在气瓶阀门后增加了一个单向阀，以保证内部最小压力相同，减小实验测量误差。

开始实验后：采集角度、压力、温度、速度等数据；之后启动电机，电机带动左侧皮带轮运动，然后通过曲轴使左活塞和右活塞进行垂直运动；而后调节电机转速，通过转速计确认转速是否达到所需测量频率；最后等待1 min，当气瓶上减压阀压力示数不再波动后进行数据采集。

2.2 模拟独立性验证

为了验证基于FVM的CFD模型以及3.4节实验结果，按照实验台的实际尺寸，采用网格划分软件ICEM进行建模，之后再利用Fluent软件进行模拟计算。

Study on Foreign Language General Education Curriculum Construction Strategy in Higher Vocational Colleges ___________________WANG Wenxuan,DING Guomao,FENG Yonghong 74

采用动网格模型，通过用户自变量函数（UDF）导入，活塞速度为：

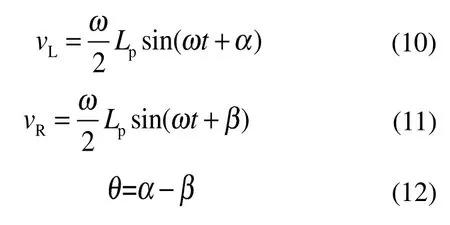
式中：vL、vR为左、右侧活塞速度，m/s；角速度，rad/s；Lp为活塞行程，m/s；为相位角；为相位差。

采用k-湍流模型、二阶迎风格式对压力、能量等进行离散。内部气体类型设置为理想气体，其黏度、热导率、比热容等参数与孔隙尺度模拟一样，通过REFPROP软件进行拟合，拟合的压力和温度范围由实验确定。4个冷却器壁面条件均为恒温壁面，温度由热电偶测得，操作压力为0，初始化内部压力由压力传感器测得。

分别建立了100万、300万、500万3种网格数量的模型对比回热器两端的压降，如图4所示。由图4可知，300万及以上数量网格模拟结果与实验结果相差不大。因此，本文采用300万网格。

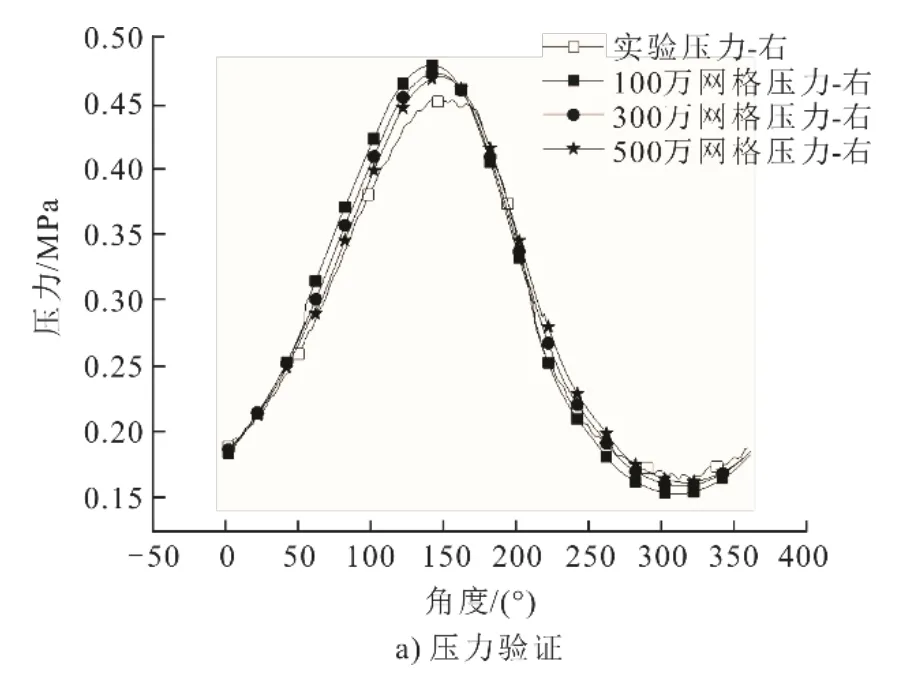
图4 网格无关性验证Fig.4 The grid independence verification

3 结果分析

3.1 基于FVM的CFD模型验证

为了验证基于FVM的CFD模型的准确性，对空气进行了若干个工况（表6）的模拟，结果如图5所示。

表6 空气工质模拟工况Tab.6 The simulation working conditions with air

图5 基于FVM的CFD模型空气流阻系数验证结果Fig.5 The verification result of air flow resistance coefficient by the FVM-based CFD model

表6中8个工况对应的雷诺数Re的范围是162~1 156。由图5可以看出：使用FVM模型得到的结果与Tanaka关联式的误差范围为5.47%~0.36%；与Gedeon关联式最大误差为7.52%~4.06%。因此说明该FVM模型可以用于二氧化碳流动特性的研究。

3.2 压降特性

3.2.1 温度的影响

设定曲轴转动前180°是热吹过程，即热气体加热冷丝网，后180°是冷吹过程，即热丝网加热冷气体。不同热端温度下工质压降变化如图6所示。由图6可以看出：压降在热吹过程中随热端温度升高而下降，在冷吹过程中随热端温度升高而升高。这主要是因为在热吹过程中，热端温度高，进入回热器的气体密度相对较低，因此压降较小；在冷吹时，进入回热器气体温度均为300 K，密度相同，但热端温度越高的工况其回热器丝网温度也越高，内部湍流更为剧烈，所以压降较大。

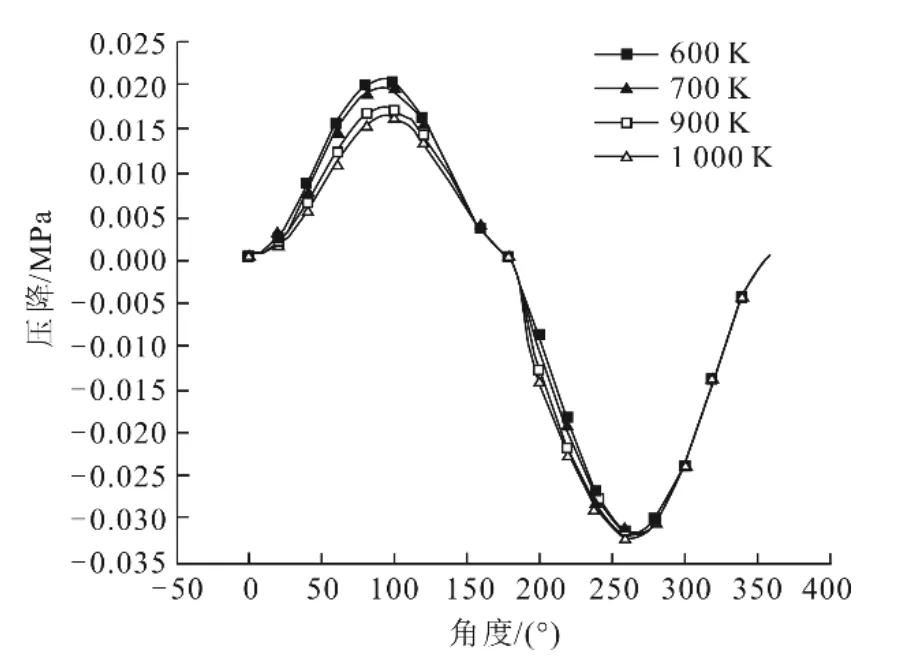
图6 不同热端温度下工质压降变化Fig.6 The pressure drop of working fluid at different hot-end temperatures

3.2.2 目数、频率、初始充气压力的影响

不同目数、频率、初始充气压力下工质的压降变化如图7所示。由图7可以看出：目数越大，孔隙率越小，压降越大；频率越高，压降越大；初始充气压力越大，压降越大。

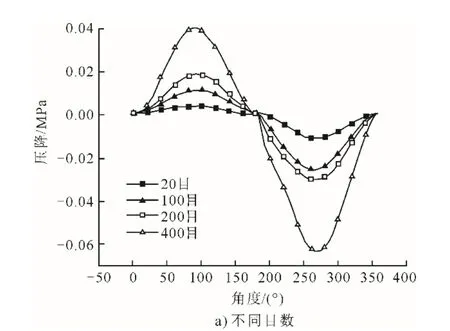
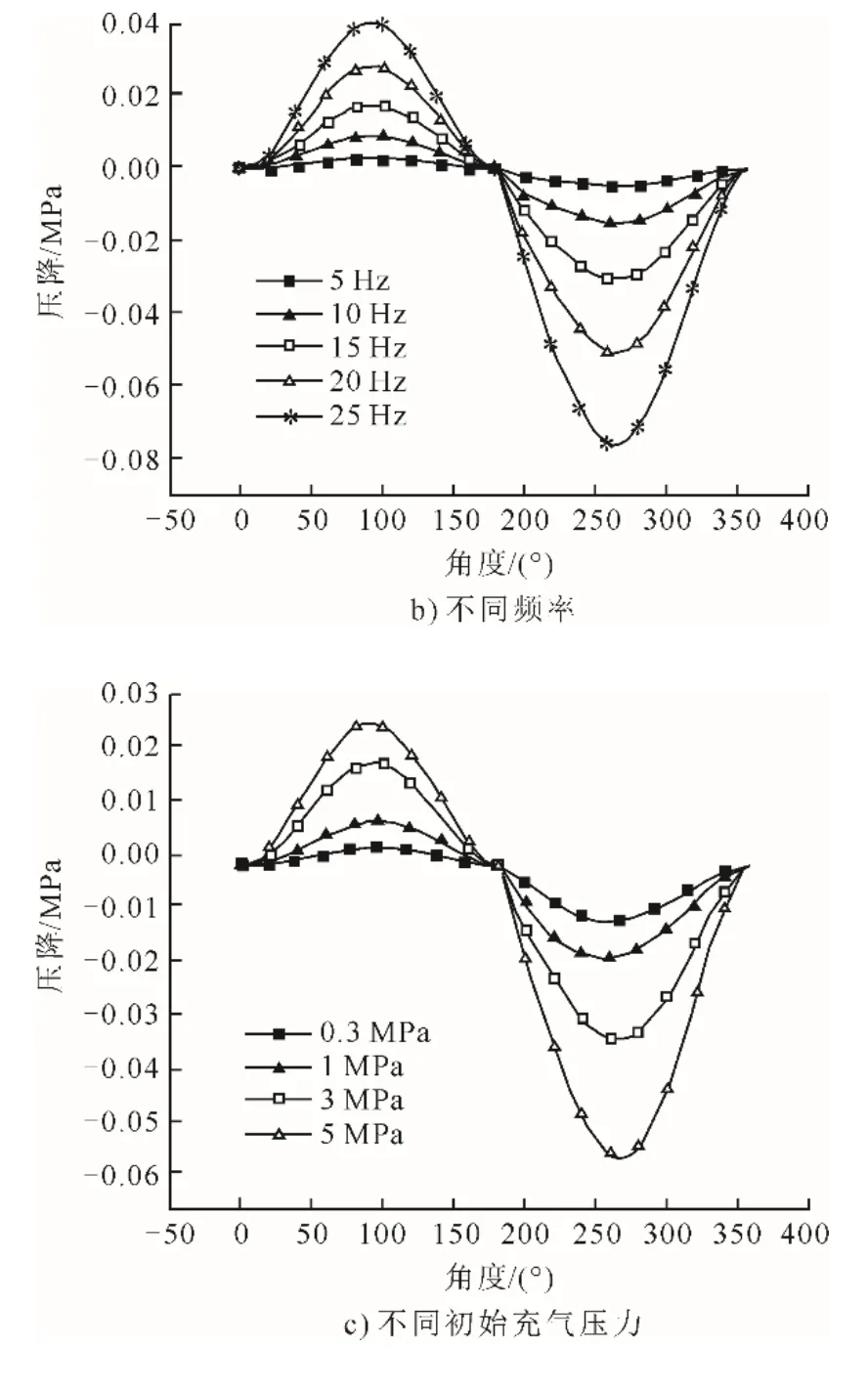
图7 不同目数、频率、初始充气压力下工质压降变化Fig.7 The variations of working fluid’s pressure drop at different meshes, frequencies and initial charging pressures

结合图6、图7可以看出，各工况下，冷吹过程的压降均大于热吹过程。这是因为热吹时，进入流域内的气体温度较高，虽然会增加气体分子内能，湍流也更为剧烈，但此时气体密度比冷吹时低很多。

3.3 摩擦特性

图8为f-Re拟合曲线。由图8可以看出：在低雷诺数下，二氧化碳气体工质的流阻系数（黑色曲线）大于空气工质（Tanaka和Gedeon等人提出的关联式，分别为紫色和绿色曲线）；随着雷诺数的升高，二氧化碳气体流阻系数逐渐接近空气工质的流阻系数。流阻系数拟合关联式为：

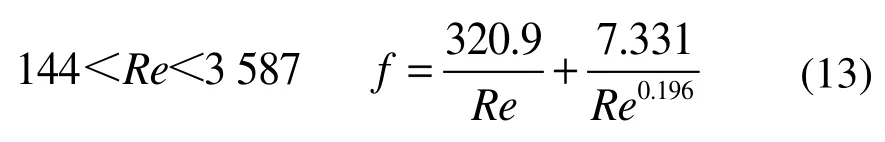
拟合得到的二氧化碳关联式在雷诺数范围内与Tanaka提出的关联式在低雷诺数下（Re＜1 733）相差大于10%，在高雷诺数下（1733＜Re＜3 587）差异小于10%；与Gedeon提出的流阻关联式最大相差47.3%，最小相差21.7%。根据Liu等人[18]的报告，该现象可以用Darcy-Forchheimer方程来解释：

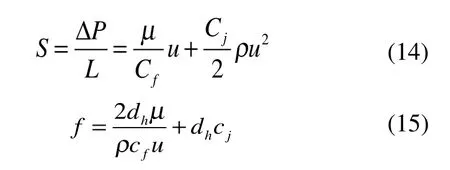
当雷诺数较大时，速度较大，此时气体物性对摩擦影响较小；但是当雷诺数较小时，速度较小，这时摩擦系数受气体物性影响较大。因此，二氧化碳和空气的流阻关联式在低雷诺数下差异较大而在高雷诺数下差异较小。

由于热吹和冷吹过程的压降相差较大（见3.2节），分别对2个过程进行分析，结果如图8所示。

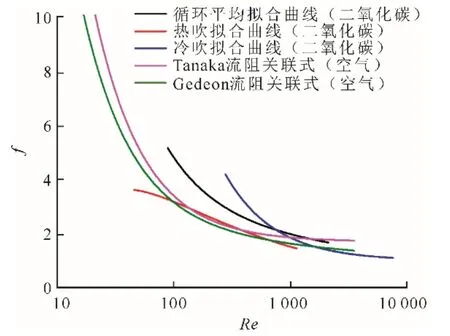
图8 f-Re拟合曲线Fig.8 The f-Re fitting curves

在雷诺数较小情况下，冷吹阶段摩擦系数大于热吹阶段，且差异明显，在所研究雷诺数Re范围内（467＜Re＜1 889），二者差异最大和最小分别为79%和32.1%。拟合公式如下：

冷吹过程：467＜Re＜13 361

热吹过程：75＜Re＜1 889

冷、热吹过程由于温度不同，工质黏度和密度变化较大，如图9所示。因此，冷、热吹过程的流阻系数存在差异。

3.4 振荡流模型验证

将式(13)带入振荡流模型（Fluent多孔介质模型），对比相位角为90°和180°的实验和模拟结果，如图10所示。由图10可以看出：相位角为90°时，空气平均压降的实验结果为0.041MPa，模拟结果为0.044 MPa；二氧化碳平均压降的实验结果为0.05 MPa，模拟结果为0.052 MPa。同时，实验和模拟中，所有工况的左、右2个测点所得最大和最小压力误差也小于7.3%，实验曲线存在一点偏移。这是由于，实验中左、右活塞相位差存在1°~2°误差，并非完美（达到90°），但在模拟时，左、右2个活塞可以准确设定为90°不变。由此可以认为该振荡流模型可以运用于研究二氧化碳工质循环率的修正。

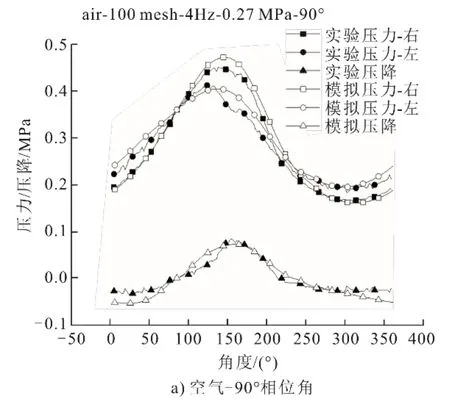
图10 振荡流模型验证Fig.10 The verification result of the oscillation flow model

3.5 循环率修正

在实际设计回热器时采用的是气体的理论循环质量，并根据式(18)初步判断回热器的孔隙率及外径或体积[19]：

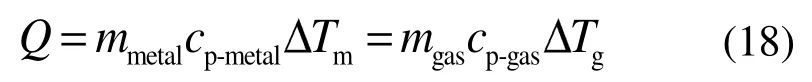
由于存在滞后特性，回热器中的质量流量和理论质量流量存在差别，在设计时可能导致回热器能力未能得到充分发挥，同时还增加了流阻损失。因此，利用循环率来讨论斯特林发动机不同截面的平均质量流量。通过Fluent得到各截面的瞬时质量流量，然后对各截面1个循环内的质量流量进行积分，得到每个截面的循环质量Mcr，理论循环质量Mct则是根据式(18)计算。再提出循环率（cycle rate）的概念，即各截面的气体循环质量与理论循环质量之比：

在模型中取了7个截面：左气缸出口截面、左中心截面、左测试面、回热器中心面、右测试面、右中心截面和右气缸出口截面，分别记作截面1、2、3、4、5、6、7（图5）。

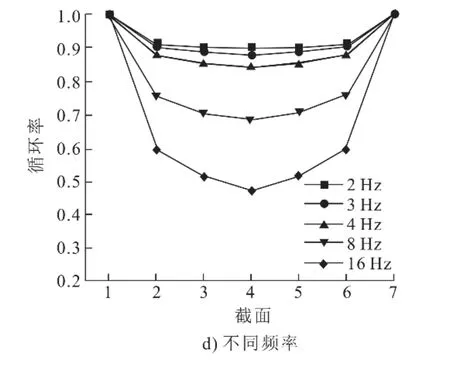
图11 不同工况下各截面循环率Fig.11 The cycle rate of each section under different working conditions

由图11a)可以看出，由于各种流阻的存在，循环率无法达到100%，即内部真实进入回热器的质量流量与设计工况存在区别。在即将进入回热器之前，空气和二氧化碳在截面4的循环率分别是86.1%、84.1%，这种现象在不同目数和频率的工况下更为明显（图11c)、图11d)），200和400目丝网截面4的循环率分别是76.9%、59.4%，3 Hz和16 Hz循环率分别是87.9%和47.2%。

然而，充气压力对整体循环率影响十分有限（图11b)）：充气压力为0.11、0.46 MPa时，截面4的循环率仅相差2.3%。

整体来说，该模型循环率分布主要呈现类抛物线形状，但其最低点出现在截面2附近，这是由于压缩腔和膨胀腔体积不同，初始位置时两侧活塞到中间回热器的距离不同。

根据图1c)和图11d)中截面4的结果拟合出2个回热器入口处的循环率为：

（R2=0.997 3，f为频率）；

在设计斯特林发动机内部回热器时，可以根据式(21)—(22)对实际的质量流量分布做出更为准确的判断，设计更为合理的回热器。

4 结 论

1）压降与金属丝网目数、发动机频率、充气压力成正相关；热端温度越高，热吹过程压降越小，但冷吹过程压降越大；同时，冷、热吹过程由于密度不同，其压降不同。

2）拟合得到了流阻关联式。由于冷、热吹过程温度不同，工质黏度和密度差异和变化较大，2个过程中流阻系数产生差异，建议在冷、热吹过程采用不同的关联式，以确保计算结果更为准确可靠。

3）对比二氧化碳与空气的流阻关联式后发现，二氧化碳的流阻系数在模拟工况范围内（144＜Re＜3 587）大于空气的流阻系数，在雷诺数较低（Re＜1 733）时相差大于10%，但在高雷诺数下（1 733＜Re＜3 587）差异小于10%。

4）获得了滞后角度回热器入口处循环率的关联式，可以将其应用于回热器设计程序中，进而确定回热器中真实质量流量，指导基于二氧化碳工质的斯特林发动机设计。