脉冲激光雷达最大测程的设计与估算方法研究

邓 全,吴淦华,陈 康,牛 群

(中国电子科技集团公司第二十七研究所,河南 郑州 450047)

1 引 言

脉冲激光雷达以其作用距离远、测量精度高、抗干扰能力强等优点,在军事领域得到了广泛应用。它主要为武器火控系统、搜瞄跟踪系统等提供目标距离信息,可使武器系统的首发命中率高达80 %以上,大幅提高了武器系统的攻击力和准确性[1]。

最大测程是反映脉冲激光雷达测距性能的关键指标,也是其综合性能的体现。最大测程的设计是一个自上而下分解指标、自下而上实现指标的过程,也是一个逐步优化、反复迭代的过程。激光雷达完成研制后,如何科学合理地检测、快速估算其最大测程,一直是业界探讨的焦点,也是用户关注的重点。有鉴于此,本文从设计的角度,对影响激光雷达最大测程的因素进行分析、探讨,简要地给出整机设计中的考虑因素；在比较当前检测方法优、缺点的基础上,深入研究快速评判最大测程的估算方法。这些研究对于推动激光雷达最大测程的设计、评估具有重要的实用价值。

2 最大测程的设计

2.1 激光雷达测距方程研究

激光雷达测距方程是最大测程设计的理论依据。它的假定条件主要包括:1)激光光束内的能量分布是均匀的；2)激光发射、接收光学和跟踪瞄准系统的光轴是严格平行的；3)激光在大气中的传输遵循几何光学规律,而大气是均匀的、各项同性的。虽然它是在一系列简化条件下推导的,但却对系统设计有着重要的指导意义[2]。按测距目标类型划分,激光雷达可以分为漫反射(非合作目标)测距和镜面反射(合作目标)测距两类。

2.1.1 漫反射测距方程

当目标表面是粗糙的无规表面(目标表面的粗糙度大于激光波长)时,即认为是漫反射目标,此时反射信号将在较大范围内散射[3]。当目标在光束方向上的投影面积小于激光光斑面积时称为小目标,反之称为大目标[4]。对于收发合置的测距系统,漫反射激光雷达测距方程可分为如下形式:

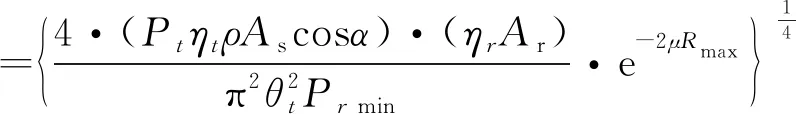
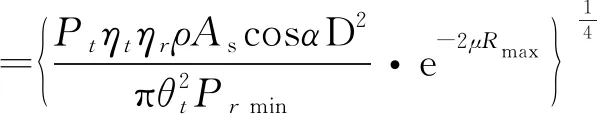
(1)

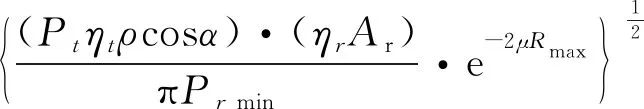
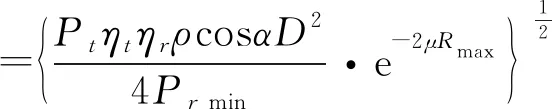
(2)

式中,Rmax为激光雷达最大测程；Pt是激光发射功率；Prmin为满足准测率的最小可探测功率；ηt、ηr分别是发射和接收光学效率；As、Ar分别是目标面积和有效接收面积；θt为激光束散角；ρ为目标反射率；D为接收机孔径；e-2μR为光源到目标的双程大气透过率,其中μ为激光通过大气时的气溶胶消光系数；α为目标表面法线方向与激光光束入射方向的夹角。

2.1.2 镜面反射测距方程

当目标表面是光滑的反射面(表面粗糙度近似或小于激光波长)时,即可认为是镜面反射目标。合作目标是一种典型的镜面反射,如无源角反射体(角反射器阵列、角锥棱镜)、面反射镜等。近年来,使用合作目标进行激光测距的应用越来越广泛。

镜面反射激光雷达测距方程为:

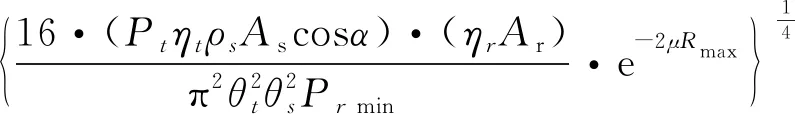
(3)

式中,As为合作目标有效入射截面积;θs为合作目标后向反射束散角(约为10-5～10-6rad);ρs为合作目标表面反射率(约为0.8～1),其余参数定义同上。由于合作目标将大部分入射激光在光学衍射极限内沿照明瞄准线原路反射,因此cosα近似为1。此外,θs比θt约小两个数量级以上,对比公式(3)和公式(1)、(2),可以看出使用合作目标测距的巨大优势。

2.1.3 工程实践中的测距方程修正

工程中,实际测试结果表明:

1) 激光束横截面的能量分布并不是均匀的,实际的能量分布与基膜或低阶膜光束的高斯分布比较接近,图1为某型设备激光光束能量图。光束能量的不均匀性对大目标测距影响不大,但对小目标测距影响较大。

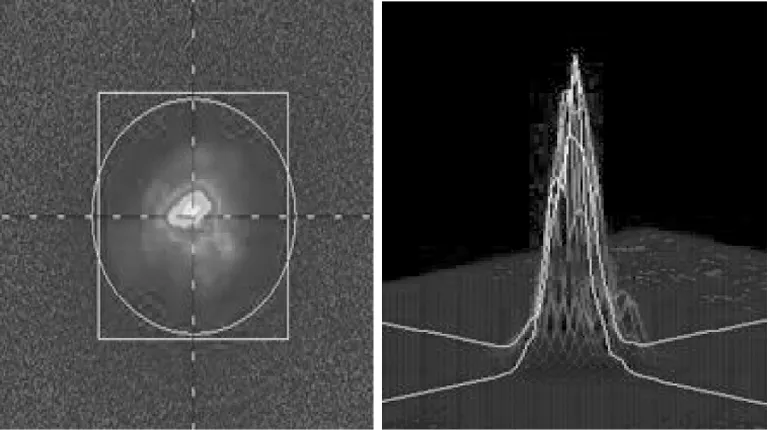
图1 某型设备激光光束能量图

2) 发射光轴、接收光轴与系统瞄准光轴并不是严格的平行关系,存在一定的轴系误差。显然,发射光轴中心与目标截面中心之间的距离满足:d=Rmax·φ,式中:d表示两中心的偏差距离,Rmax表示探测的最大测程,φ表示光轴及瞄准误差(mrad)。可以看出,φ越小,目标就越靠近激光照射中心,反射的激光能量就越强,相应地激光雷达最大测程越远；反之,则越近[5]。

为了使测距方程理论计算结果与工程实践结果较为一致,需要对测距方程进行修正。限于篇幅,本文直接给出修正后的激光雷达测距方程。式中φ表示光轴及瞄准误差,其余参数定义同上。

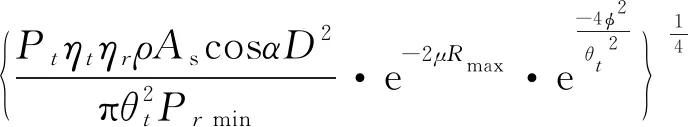
(4)

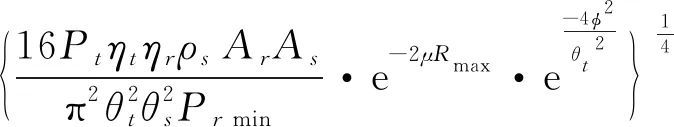
(5)

2.2 大气双程透过率的计算

大气双程透过率是影响激光雷达测距性能的主要因素之一,但在设计中容易被忽略。激光在大气中传输时,由于激光辐射和大气的相互作用将导致激光束自身特性变化,主要包括:湍流效应、衰减效应、热畸变效应和大气击穿效应。对于发射功率为中小功率的激光测距系统,主要考虑湍流效应和衰减效应[3]。

湍流效应会改变大气折射率,引起激光束的强度起伏(闪烁效应)、光束抖动、光斑漂移和光束扩展等[3],并影响激光雷达的跟踪测量性能,使其测程减小、精度变差。因此,激光雷达最大测程的室外测试一般要求天气晴朗、无风(微风)、气流相对稳定等环境条件。

衰减效应的主要因素是:大气分子吸收、散射和气溶胶散射等。对于近红外激光来说,其衰减主要由气溶胶散射引起,而其他衰减因素相对可以忽略[6]。气溶胶消光系数一般用能见度来描述,工程中常用经验公式(6)来估计水平方向(平程)气溶胶消光系数:

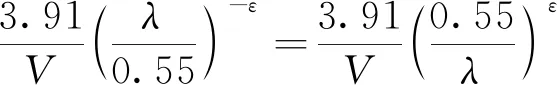
(6)

式中:V为能见度；λ为激光波长；ε为经验数,它的取值和大气能见度密切相关,并由下式确定:

(7)

用Tλ表示大气单程透过率,则平程大气双程透过率Tλ2为:

Tλ2=e-2μRmax

(8)

2.3 最大测程设计的考虑要素

通过上述分析,可以看出影响最大测程的主要因素包括:

1)发射机系统(Pt、θt、ηt)；

2)接收机系统(Prmin、D、ηr)；

3)目标特性(ρ、As)；

4)大气传输参数(λ、V、Rmax)。

因此,为设计最大测程,就必须对以上因素认真分析,经综合考虑后选取最佳参数。由于目标特性相关参数可通过查阅资料获得,本文不再赘述。

从发射机角度,可以考虑如下措施:1)提高发射机峰值功率Pt。在单个激光器功率受限的条件下,为提高发射功率可以采用串联拼接、并联阵列发射的方式。但是,提高发射峰值功率将受限于激光雷达功耗、体积、重量、散热等因素,同时也受激光器或光学元件的损伤阈值限制；2)减小激光束散角θt。为满足不同距离段对束散角的要求,可以考虑无焦变倍准直扩束设计以实现对束散角的连续可调[7]。当然,激光束散角θt不可能无限减小,它必须与武器系统的跟踪精度相匹配。一般地,激光束散角需满足θt≥2(δmax+r/Rmax)≈2.5δmax,式中r为目标截面径向距离,Rmax为最大探测距离,δmax为系统最大跟踪误差。

从接收机角度,可以考虑如下措施:

1)增大接收口径D。相应地,这也受到整机结构、体积、重量的限制；

2)提高接收光学系统对光路中背景杂散光的抑制能力。除了常用滤光方法外,采用挡光环大口径非球面接收光学系统设计,不仅能够有效抑制杂散光提高光学增益,而且可以减少镜组数量实现系统的轻量化、小型化[7]；

3)减小接收机最小可探测功率Prmin。一般而言,光电探测器的灵敏度与器件的工艺水平密切相关,提高器件灵敏度难度很大。但是,可以通过接收信号处理系统的优化设计,利用信号的相关性和噪声的非相关性,通过优化算法,达到“抑制噪声干扰,提高整机信噪比”的目的[8]。这些方法包括:动态阈值检测、恒虚警处理、单/多脉冲信号累积、脉冲串互相关算法、全通道波形采样等。

从大气传输参数的角度,首先要根据目标背景特性、任务需求及环境适应性等要求,选择合适的激光波长。目前,激光雷达可以采用0.53 μm、0.63 μm、0.8～0.9 μm、1.06 μm、1.54 μm、2 μm和10.6 μm等7个波长段[9]；其次,测试最大测程时要求有较好的天气条件。

3 最大测程的检测

激光雷达完成设计、加工、联试后,需要对激光雷达最大测程进行检测。现行最大测程的检测方法主要有:实际测距法、消光比法[10]。

3.1 实际测距检测法

实际测距法是最直观的检验方法。武器系统鉴定试验中,一般通过目标动态检飞来测试该项指标。实际测距法的优点是简单、直观；缺点在于:1)对试验条件的要求较高,如协调真实目标、满足能见度的天气等较难实现,不适合设备平常的检验过程；2)受天气能见度影响很大,试验重复性差,结果可比性差；3)试验成本高。

3.2 消光比检测法

消光比法是通过在激光雷达的发射或接收光路中加入衰减器,以模拟大气传输及目标距离对激光的消光效果,进而模拟检测激光雷达最大测程的一种方法。消光比法检测原理如图2所示,在距离激光雷达R(通常取500 m)处架设一标准漫反射测试靶,靶面反射系数为ρ且靶面积大于发射激光光斑面积,在激光雷达发射光路中加入衰减器,瞄准靶板进行测距,改变衰减器的衰减量,直至被测设备达到临界稳定测距状态,此时的衰减量即可反映激光雷达的最大测程。

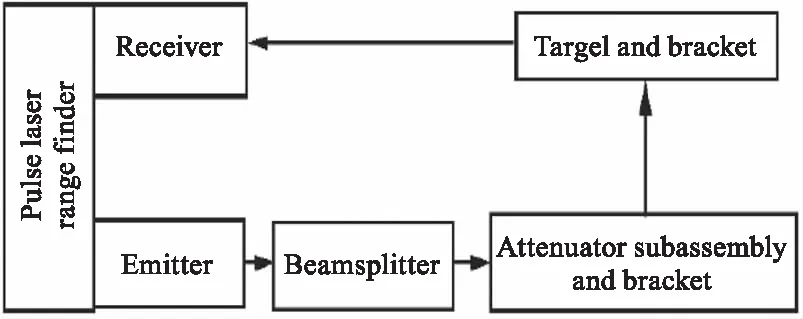
图2 室外消光比检测原理框图

消光比法的优点是能够较好地克服天气条件的影响,但是架设标准靶板的方法不易广泛推广。目前,激光雷达接收处理电路大都采用了时序增益控制(TGC)技术,不同型号装备的增益控制时间各不相同。这就意味着消光比测试时要么设置时序增益控制开关,要么实时测出接收时序增益电路的增益比G(R2)/Gmax,对于用户使用很不方便。从测试结果看,消光比法只能定性地给出最大测程是否满足要求,不能直观、定量地给出最大测程值。因此,消光比法只适用设备研制生产、出厂验收过程,不适宜用户野外使用场合[10]。

4 最大测程的估算

本文通过对测距方程的深入研究,给出了两种最大测程的估算方法:直接计算法和比例计算法。

4.1 直接计算法

当激光雷达完成研制后,则主要的技术参数均已确定,光轴及瞄准误差也可测量得出。根据公式(1)～(5),此时激光雷达最大测程主要受大气能见度V和目标法线与入射光束之间夹角α的影响。当α=0时,最大测程仅与不同大气能见度V有关。

将激光雷达已经确定的各项参数代入测距方程,可以得到简化的方程形式:

(9)

式中,A、B为经计算后的常数项；V为不同大气能见度,是一个变量；Rmax为待求的最大测程。该方程是关于Rmax的超越方程,可用迭代法、牛顿切线法等算法求解[4]。这种方法将测距方程的参数分为常量和变量,其中常量的计算可以通过程序设计实现,变量只需要改变能见度参数,即可计算不同能见度下的最大测程,计算过程简单、快捷,制约因素较少。工程实践中,为降低恶劣天气湍流效应对激光光束的扩展影响,在计算时可将理论束散角扩大25 %带入计算,即:θt′=1.25·θt。

4.2 比例计算法

这种算法的总体思路是:经比例换算,将已知条件下不发生改变的参数约分,再通过实测的最大测程,估算特定条件下的最大测程。实践中常用的估算情形如下:

(1)已知能见度V1所对应的最大测程Rmax1,求解能见度V2对应的最大测程Rmax2。

在这种测试条件下,激光雷达自身的参数不会发生变化,则:

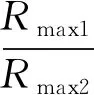
(10)

特别地,对于天基激光雷达而言,在地面建立准确模拟太空环境的测试条件技术难度大、投资成本高。因此,天基激光雷达最大测程通常采用比例计算法,用地面测试数据推算在太空环境下的最大测程。将太空环境下Tλ太空=1,代入公式(10),可得:

(11)

该方法对于激光雷达最大测程的验收测试具有重要的应用价值。这意味着激光雷达最大测程验收时,不必完全依赖试验大纲要求的天气条件,可以节约大量的试验成本。缺点在于大气能见度具有一定的主观性,按此方法计算的最大测程差异较大。

(2)假定在同一能见度条件下,接收口径为D1得到最大测程Rmax1,求解设计接收口径D2对应的最大测程Rmax2,则:

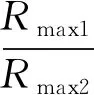
(12)

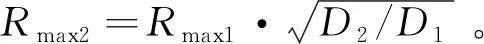
(3)假定发射功率Pt1对应最大测程Rmax1,因设备长时间服役、维修等原因造成激光发射功率下降,现求解发射功率下降后Pt2所对应的最大测程Rmax2,则:

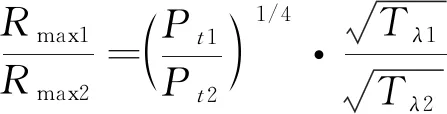
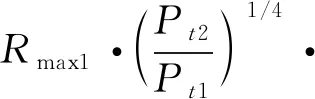
(13)

当设备性能下降后,用户一般会协调厂家进行测试维修,这无疑增加了时间、人力、物力等成本。在战时紧急情况下,可以指导用户采用该方法快速判断、评估设备性能下降是否影响作战任务。显然,这具有重要的实战价值。

4.3 快速估算实例

下面以小目标测距为例,利用上述方法快速估算激光雷达在各特定条件下的最大测程。

4.3.1 直接计算法实例

某型激光雷达完成设计后,将各参数代入公式(4),得到超越方程:

(14)

用迭代法求解该方程,并带入指标要求的能见度20 km,可得相应最大测程为20.13 km。代入不同能见度,可得相应最大测程,计算结果见表1。

表1 不同能见度下最大测程(单位:km)

4.3.2 比例计算法实例

(1)不同能见度比例法

假设某激光雷达外场鉴定验收时,能见度V1=9 km,实测最远距离为13.44 km,求解指标要求能见度20 km下的最大测程。

将相应参数代入公式(10),可得:

(15)

求解关于Rmax2的超越方程,可得最大测程为20.13 km。

某型天基激光雷达在地面能见度V1=18 km,实测最远距离为11.4 km,根据公式(11),解算得到太空环境最大测程为21.8 km。在后续的空间飞行试验中,该型激光雷达在22.2 km发现目标,稳定跟踪距离为21.2 km。试验结果表明:采用该方法计算的最大测程理论值与实际测试值基本一致,从而也验证了该方法的正确性。

(2)遮挡口径比例法

某型激光雷达在外场摸底试验时,由于真实目标不易获得,采用遮挡口径法获得对模拟目标最大测程,依据公式(12)求解对真实目标的最大测程。试验参数及结果见表2。

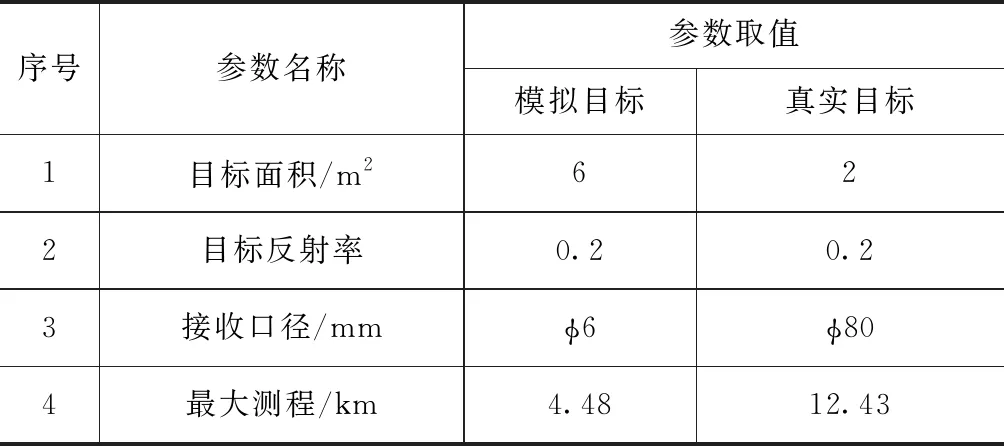
表2 遮挡口径法试验参数及结果

当测量的模拟目标与真实目标一致时,则最大测程为16.36 km。

(3)发射功率比例法

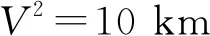
将各参数带入公式(15),可得:

(16)

求解关于Rmax2的超越方程,可得最大测程为13.58 km。特别地,当能见度V1=V2=20 km,计算可得最大测程为19.03 km。从计算结果可以看出,在其他条件相同时,发射功率下降33.33 %,其对最大测程的影响并不明显。

5 结 语

围绕激光雷达最大测程这一重要指标,文中研究了脉冲激光雷达测距方程,并对影响最大测程的因素给出了设计考虑。文中大气透过率是按照平程计算的,实践中常要计算斜程大气透过率,但这并不影响文中各公式的正确性。当前,检测激光雷达的方法存在着使用不便、制约因素多等缺点。文中提出的不同条件最大测程的估算方法,具有计算量少、成本低、结果直观、应用广泛灵活等优点。这些估算方法立足于工程实践,能够更好地指导用户开展性能检测、维修评估等工作,具有较高的推广应用价值。