基于PCA-CLEAN的噪声稳健激光微多普勒特征提取方法
罗宗誉,严华林
(1.广东省电子信息高级技工学校,广东 广州 510450;2.广西大学计算机与电子信息学院,广西 南宁 530000)
1 引 言
雷达发射信号照射到运动目标时,回波信号的频率相对于发射信号频率会产生一个频偏,这种现象被称为多普勒效应,根据多普勒频偏可以计算出目标的运动速度,激光雷达就是基于该原理实现测速。如果目标在运动的同时,其上的组成部件还存在着振动、旋转等微运动,这些微运动会在目标多普勒频率两侧产生周期性的频率调制,Chen将这种现象称为“微多普勒效应”[1]。微运动和微多普勒效应在自然界中广泛存在,例如人走路时四肢的摆动,鸟飞行时翅膀的煽动,飞机巡航过程中旋翼的转动等等。微运动和微多普勒效应与目标的几何结构和运动特性紧密相关,是雷达回波中目标信息独一无二的表现形式,能够用来对目标的类别和属性进行判断[2-4]。激光相干雷达具有分辨率高,隐蔽性好和抗干扰能力强等优势,相对于微波雷达,其波长更短,因此利用激光雷达实现对目标微多普勒效应的探测和分析具有天然优势,激光雷达中微多普勒效应的研究成为了近年来的热点[5-9]。
直升机和螺旋桨飞机在战争中承担着不同的作战任务,威胁程度不同,因此在战场环境中实现对两类飞机的分类识别具有重要意义。当前国内外对空中飞机目标进行分类识别的研究主要集中在两个方面:一是参数估计类方法,该类方法需要首先将回波中占主要能量的机身分量进行去除,然后提取微多普勒调制中的调制周期或谱线间隔等参数,并从其中反演出桨叶尺寸或桨叶转速等信息从而实现目标分类,该类方法将回波中提取的信息与目标的物理模型联系起来,物理含义清晰,易于理解,缺点是为了获得较高的参数提取精度,需要较长的观测时间积累[10-11];二是特征提取类方法,该类方法通过特征提取的方式将目标回波中的差异信息进行提取,然后利用SVM等分类器实现分类识别。需要指出的是,不同目标的差异信息并不仅仅存在于时域回波,回波的频域、时频域等变换域在一定条件下也能够很好的反应出不同目标的调制差异,同样被广泛用于特征提取。特征提取类方法在较短的观测时间下即可实现目标分类,但是由于回波中微动分量能量相对于机身分量较小,提取的特征中微动分量作用相对较弱,难以充分描述回波中的微多普勒调制差异[12-16]。
本文在前述研究的基础上,针对回波中微多普勒分量能量较弱,易被噪声污染的问题,提出一种基于PCA-CLEAN算法的噪声稳健分类方法,首先利用PCA方法对低信噪比的回波信号进行噪声抑制,然后利用CLEAN算法将回波中的机身分量和微动分量分离,进而提取反应不同目标微动差异的三维特征构成特征向量,最后利用SVM分类器实现分类。基于仿真和实测数据的试验结果表明,所提方法可以获得较好的分类性能。
2 飞机旋转部件激光回波模型
假设激光雷达发射的相干信号为:
st(t)=exp(jω0t)

s(t)=a(t)exp(jω0t+φ(t))
其中,a(t)为幅度调制函数;φ(t)为由目标运动和微运动引起的相位调制函数。假设飞机旋转部件由N发旋翼构成,目标运动速度为v0,桨叶旋转速度为wr,则根据雷达方程可以构建旋翼的回波模型为[2]:
(1)
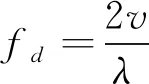
(2)
为了更好地分析旋翼的微多普勒调制特性,将式(1)转换至频域,得到回波信号的频谱为:
(3)
其中,δ(·)为Dirac函数。从式(3)可以看出理想旋翼回波由以fd为中心,周期为nmfrm的一组谱线构成,谱线幅度cmi受桨叶长度,激光波长等多种因素影响。
在雷达对目标探测的较短时间内,目标机身可以看做是以恒定速度运动的点目标,此时机身分量的回波信号可以表示为:
sF(t)=cFexp(j2πfdt)
(4)
除了微动分量和机身分量外,回波中不可避免的会含有噪声分量,则激光雷达回波信号x(t)可以表示为:
x(t)=s(t)+sF(t)+n(t)
(5)
其中,n(t)为零均值高斯白噪声。
图1给出了仿真得到的直升机和螺旋桨飞机的激光探测回波时频图,并在图中对微动分量、机身分量及“闪烁”现象进行了标注[8]。可以看出两类飞机的雷达回波中微多普勒调制分量存在明显的差异。仿真结果与文献[5]中雷达实测数据一致,表明上述模型符合实际情况。同时从图1可以看出,机身分量在回波中占据主要能量,微动分量较弱,如果直接对回波信号进行特征提取,将会导致三类目标微动分量的差异不能在特征中充分的体现,因此在特征提取前需要将机身分量与微动分量分离。
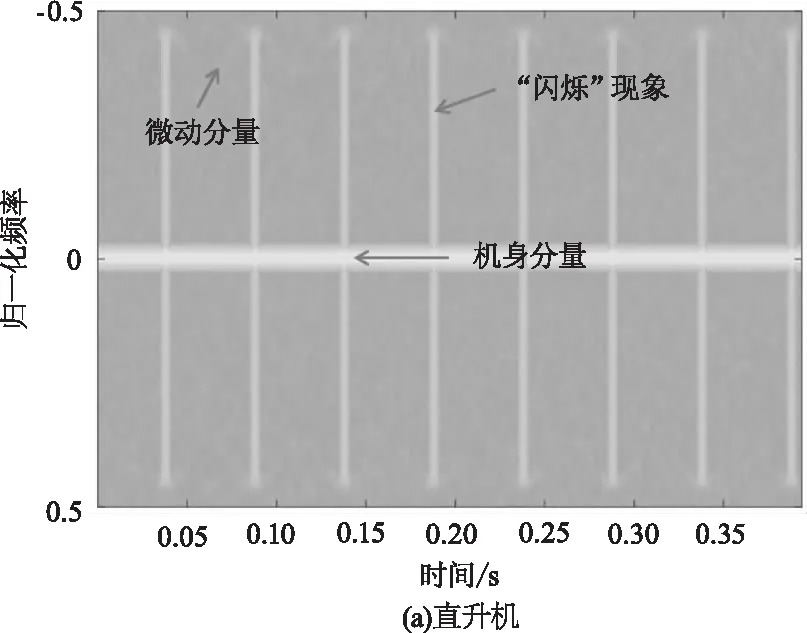

图1 两类飞机激光回波仿真数据时频图
3 基于CLEAN算法的特征提取
3.1 CLEAN算法
从上述分析可知,飞机目标的回波由一系列谱线构成,其中能量最大的谱线为机身分量,周围周期性谱线为微动分量。因此如果要将回波中的机身分量和微动分量分离,只需要在频域中找到并提取能量最大的谱线即可。CLEAN算法最初是一种用来实现对合成孔径雷达旁瓣信号进行抑制从而提升图像质量的信号去卷积方法[17],由于其具备精度高,运算量小等优势,一经提出便吸引了众多学者的关注,被广泛应用于从复杂信号中提取特定频率分量领域。对于给定信号x(t),利用CLEAN算法从其中提取最大频率分量的步骤为:
(1)将x(t)作为初始输入信号;
(2)对x(t)进行快速傅里叶变换(Fast Fourier Transformation,FFT),将其由时域转换至频域,得到x(t)的频谱X(f)=FFT(x(t));
(3)寻找并记录X(f)中最大值点对应的幅度Ax,频率fx和相位φx;
(4)利用步骤(3)的结果构建信号X(t)中能量最大的谐波信号xx(t)
xx(t)=Axexp(j2πfxt+φx)
(6)
(5)利用x(t)减去xx(t),得到去除最大谐波的剩余信号xr(t);
(6)判断xr(t)是否满足终止条件,不满足则令x(t)=xr(t),重复进行步骤(2)~步骤(5),直到满足迭代终止条件。
图2给出了利用CLEAN算法对图1所示两类飞机仿真数据提取机身分量后,剩余微多普勒分量的时频图,对比图1和图2可以看出,提取机身分量后,微多普勒调制分量在剩余信号中占据主要能量,此时进行特征提取,能够有效的将三类飞机微多普勒调制的差异进行体现。
3.2 特征提取

(7)

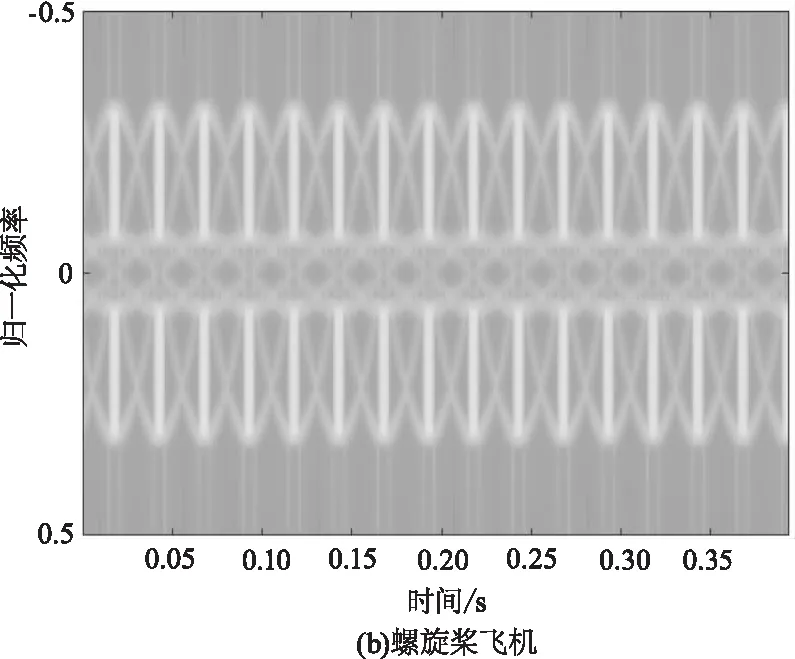
图2 CLEAN算法去除机身分量后数据时频图
提取如下三维特征描述不同目标微多普勒调制之间的差异:
特征1:微多普勒分量的熵:
(8)
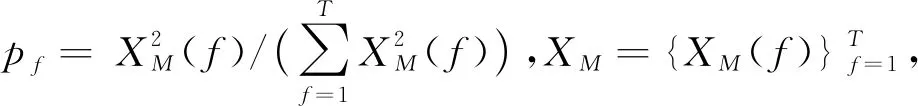
特征2:微多普勒分量的二阶中心距:
(9)
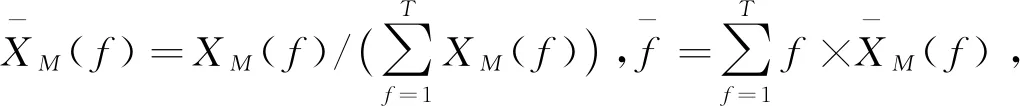
特征3:微动分量、机身分量能量比:
(10)
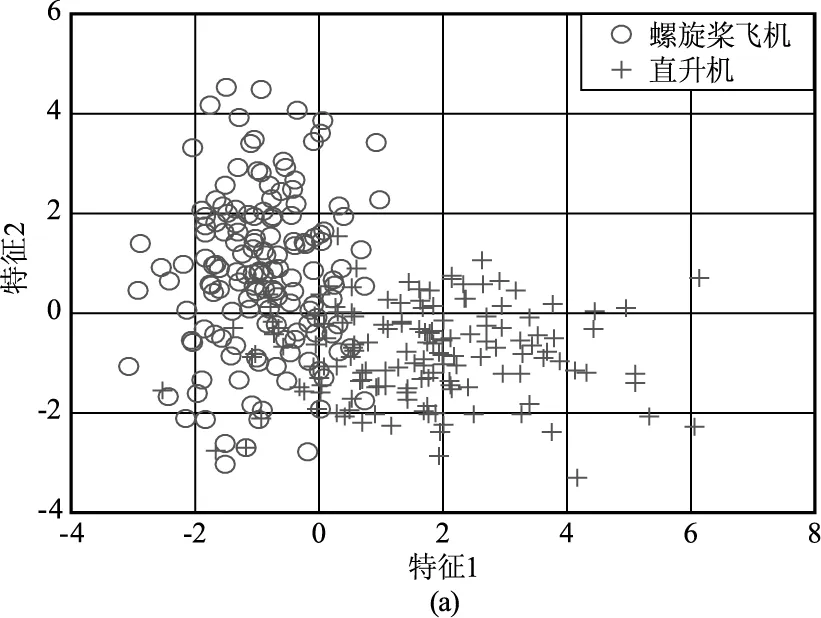
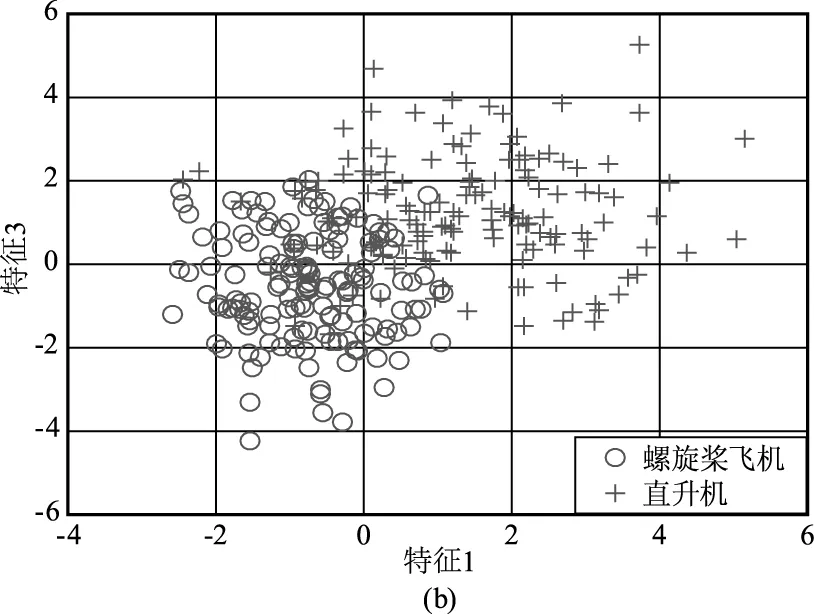
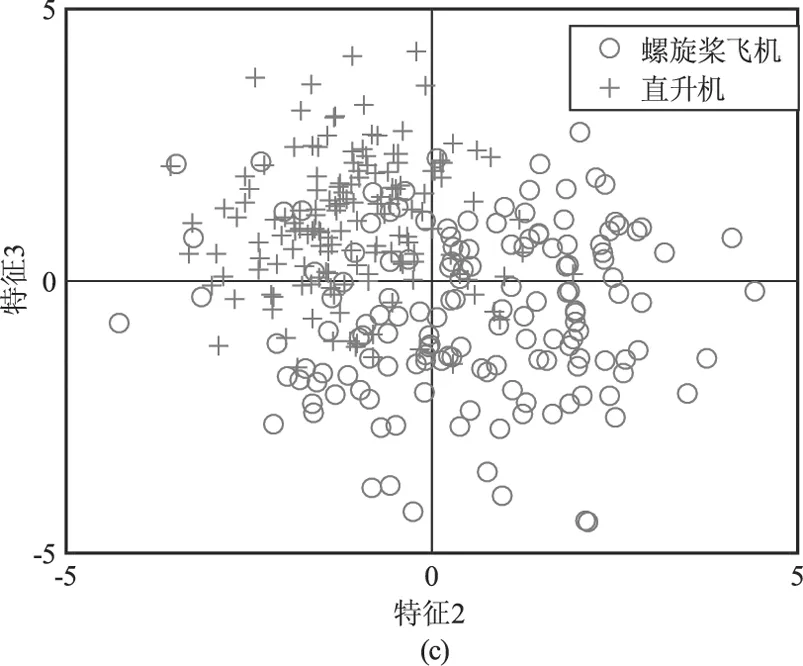
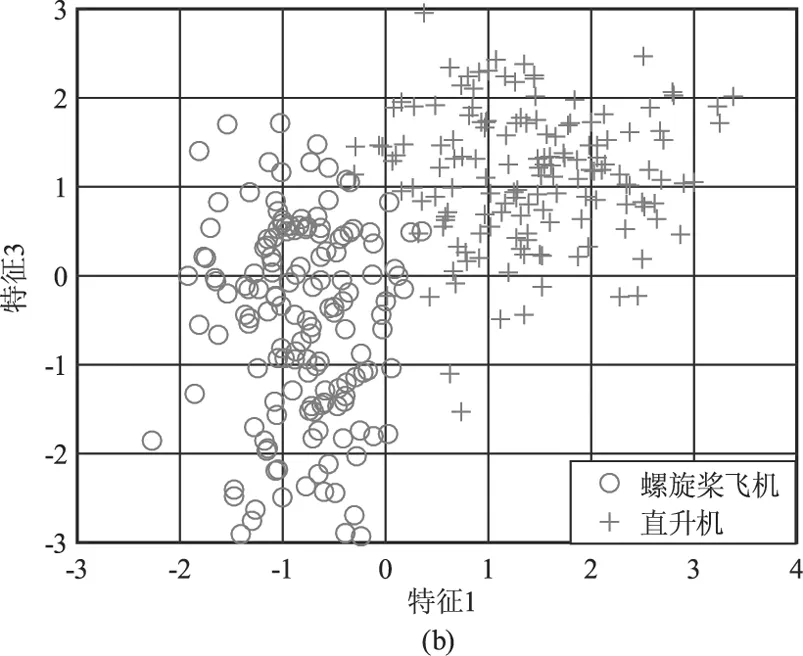
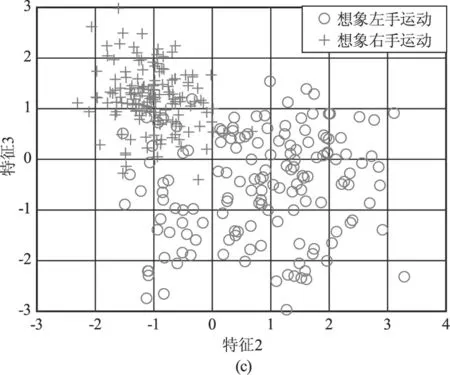
图3给出了对仿真得到的300组数据(直升机150组,螺旋桨飞机150组)提取上述三维特征的二维分布图,其中“圆圈○”表示对螺旋桨飞机回波提取的特征值,“加号+”表示对直升机回波提取的特征值,仿真过程中采用与文献[2,8]一致的参数设置,即目标距离为10 km,方位角α=0°,俯仰角β=20°,激光雷达波长为1.55 μm,表1给出了仿真过程中两类目标的典型参数值。同时为了增加数据的多样性,仿真过程中在表1所给数据的基础上增加10 %的波动范围。
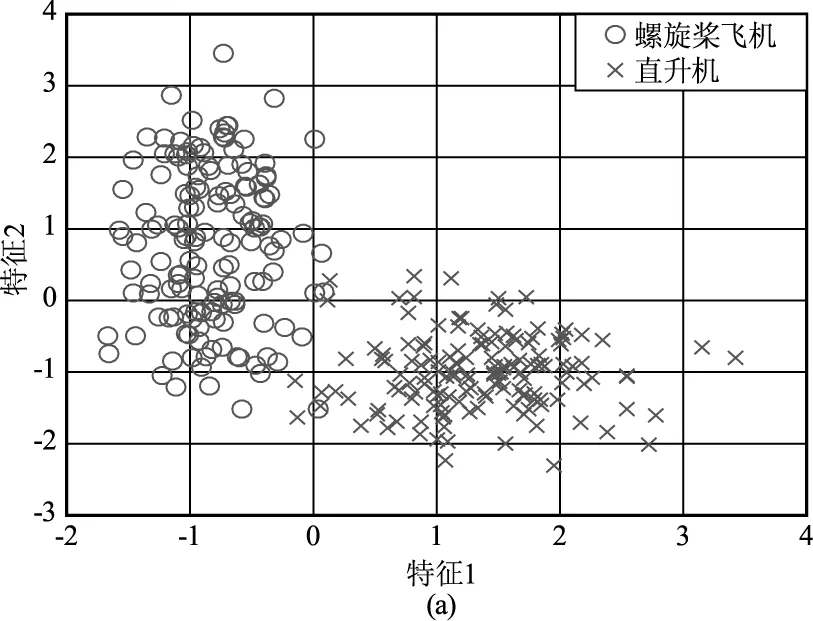
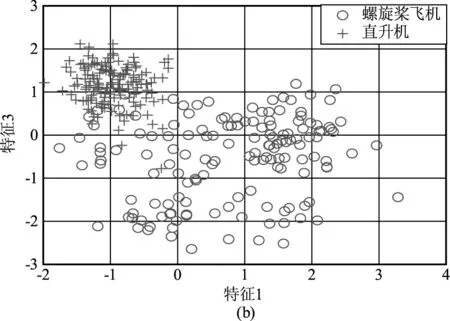

图3 对仿真数据提取三维特征的二维分布图
从图3可以看出,所提三维特征在特征域存在明显差异,具备较好的可分析。

表1 5架直升机(T),5架螺旋桨飞机(P)仿真参数
4 基于PCA算法的噪声抑制
从图1给出的仿真结果可以看出,在空中飞机目标的雷达回波中,微动分量能量较小,容易受到噪声污染,噪声的存在会对提取特征的可分性产生影响,并最终降低分类性能,因此在进行特征提取前通常需要对回波信号进行一定的预处理,消除其中的噪声分量。
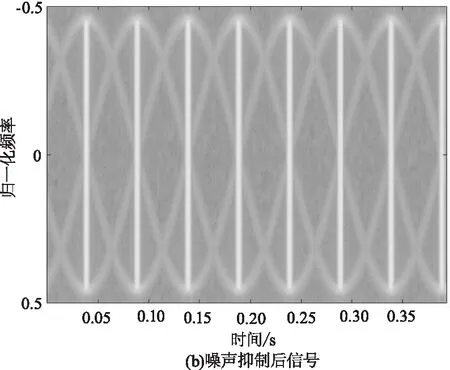
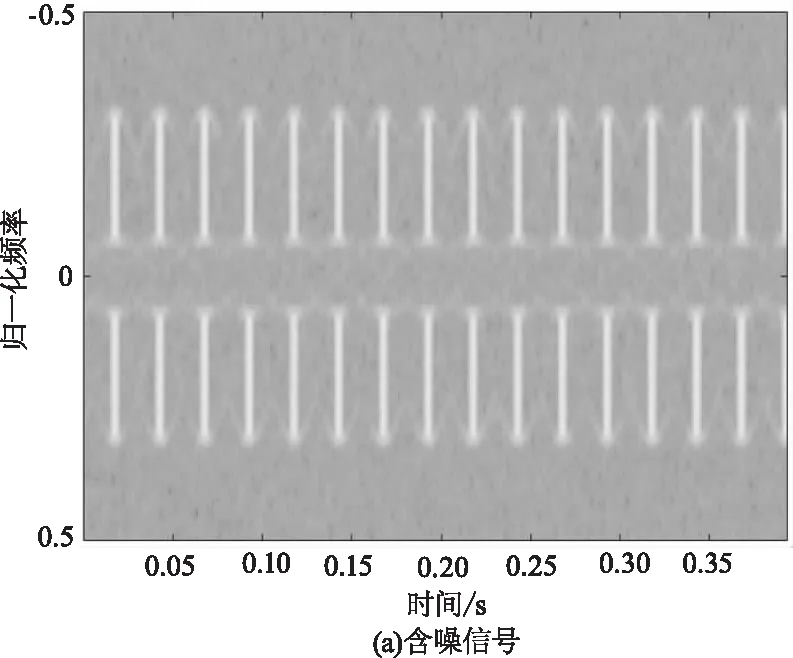
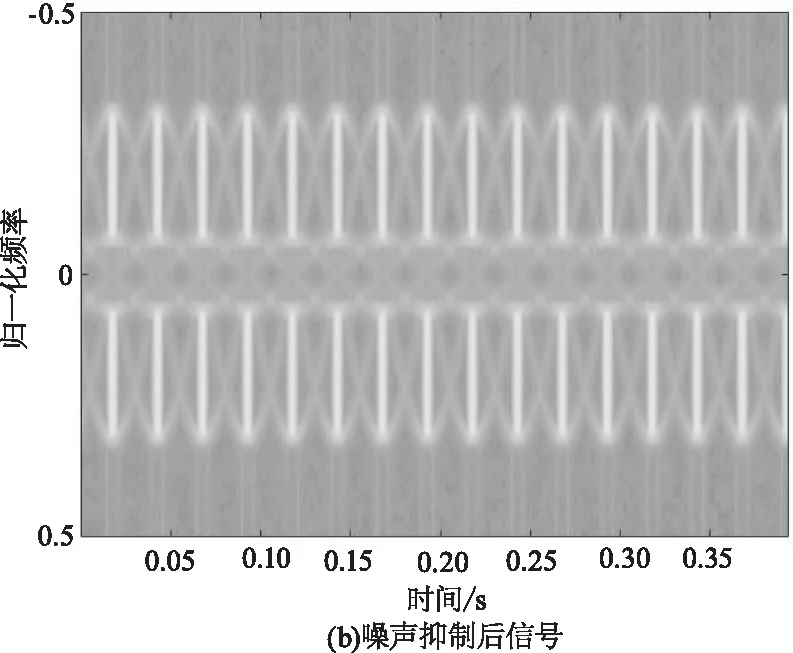
主成分分析(Principal Component Analysis,PCA)是一种经典的数据分析方法[18],被广泛应用于数据降维和信息提取。对于任意D维数据,PCA按照数据方差减小的方向依次从D维数据中提取K(K 对于激光雷达接收到的目标回波数据X=[x1,x2,…,xD]T,由于X为列向量,要计算其协方差矩阵,需要利用滑窗的方法将其转换为多个长度较短的新序列。 (11) 3)由于协方差矩阵为奇异矩阵,对其进行特征值分解,记特征向量和特征值分别为ui,λi(i=1,2,…,W),并将其按降序排列: (12) 对协方差矩阵进行特征值分解后,会存在K个大特征值及对应的特征向量,这些特征向量构成信号子空间,包含了信号中绝大部分有用信息。(W-K)个特征值相对较小,对应的特征向量构成噪声子空间,不包含有用信息。 4)选取占特征值总能量超过95 %的特征值个数为K,即: (13) 5)利用K个大特征值对应的特征向量对信号进行重构,得到噪声抑制后的信号为: (14) 为了验证上述方法的噪声抑制性能,在图2结果的基础上,向其中加入高斯白噪声,使数据信噪比降低为10 dB,得到的结果如图4(a)和图5(a)所示,可以看出叠加了高斯白噪声后,微多普勒分量被噪声污染,信号的周期性消失,导致两类目标微多普勒调制的差异性降低。利用PCA方法对含噪信号进行噪声抑制,得到噪声抑制后的信号如图4(b)和图5(b)所示,可以看出PCA方法在实现噪声抑制的同时很好的保留了原始信号中的微多普勒分量。图6给出了对信噪比为10 dB的仿真信号提取三维特征的二维分布图,图7给出了利用PCA对信号进行降噪后再次提取三维特征的二维分布图,从图6可以看出,信噪比降低后三维特征分布交叠在一起,可分性明显降低,从图7可以看出经过PCA进行噪声抑制后再次提取的特征域图3所示结果一致,特征具有较高的可分性。 图4 直升机微多普勒分量噪声抑制结果 图5 螺旋桨飞机微多普勒分量噪声抑制结果 图6 对信噪比为10 dB信号提取特征的二维分布图 图7 对信噪比为10dB信号进行噪声抑制后提取特征的二维分布图 为了验证所提方法的噪声抑制及分类性能,分别采用仿真数据和实测数据进行试验,试验过程中分类器选用SVM分类器[17],核函数为高斯核,核参数在0~5范围内遍历,并选择分类性能最好的核参数作为最优核参数。 仿真试验中将前述300组仿真数据进行划分,其中140组数据(70组直升机,70组螺旋桨飞机)作为训练数据,剩余160组数据作为测试样本,首先仿真数据中不加噪声,处理过程中也不利用PCA进行噪声抑制,直接对高信噪比仿真数据提取三维特征进行分类,分类结果如表2所示,并与传统时域特征[14]和频域特征[18]的分类结果进行对比,其中分类正确率为该类目标正确分类数据数量除以该类目标数据总数量。从表2可以看出,CLEAN算法提取特征的分类正确率要远远高于时域特征和频域特征,并且对于每一类目标,CLEAN算法提取的三维特征均能获得最优的分类性能。 表2 仿真实验分类结果 为了验证所提方法在低信噪比条件下的分类性能,采用向测试数据中加入不同信噪比高斯白噪声的方式(0~40 dB)进行试验,图8给出了不同信噪比条件下,所提PCA-CLEAN方法,不进行噪声抑制的CLEAN方法,不进行噪声抑制的时域特征和不进行噪声抑制的频域特征四种方法的分类结果。从图8可以看出,当信噪比优于10 dB时,PCA-CLEAN算法即可获得超过85 %的正确分类结果,而直接利用CLEAN算法提取特征,不提前进行噪声抑制的情况下要达到85 %的正确分类性能需要测试数据的信噪比优于20 dB。 图8 不同信噪比条件下四种方法的分类性能(仿真数据) 实测数据为某激光雷达录取的多种型号的2类飞机目标回波,激光雷达工作波长为1.55 μm,实测数据中包含64组直升机数据和56组螺旋桨飞机数据,由于实测数据录取环境为合作场景,录取的实测数据信噪比较高(约33 dB)。图9给出了一组直升机和螺旋桨飞机实测数据CLEAN处理结果,其中第一行子图为原始数据频谱,第二行子图为CLEAN算法提取的微多普勒分量,第三行子图为CLEAN算法提取的机身分量,可以看出,原始数据回波中,机身分量占据主要能量,微动分量不明显,经过CLEAN算法进行分析后,能够有效的将机身分量和微多普勒分量分离。表3给出了CLEAN算法,传统时域特征和频域特征三种方法的分类结果,训练数据采用仿真得到的全部300组数据,从中可以看出,实测数据的分类试验结果与仿真数据一致,所提方法可以获得最优的分类性能,相对于传统特征分类结果提高7 %以上。 图9 实测数据CLEAN分解结果 表3 实测数据分类结果 图10给出对实测数据添加不同信噪比高斯白噪声后,利用PCA-CLEAN算法进行噪声抑制及分类的结果,可以看出利用PCA进行噪声抑制后,能够明显提升CLEAN提取特征在低信噪比条件下的分类性能。 图10 不同信噪比条件下四种方法的分类性能(实测数据) 微运动和微多普勒效应是反映目标几何参数和运动特性的本质特征,激光雷达中微多普勒效应的提出给雷达自动目标识别技术研究提供了新的方向。本文以微多普勒效应为基础,针对战场环境下直升机和螺旋桨飞机的分类问题,提出一种基于PCA-CLEAN算法的噪声稳健微动特征提取及识别方法,并利用仿真数据和实测数据对所提方法的性能进行了验证,结果表明所提方法能够有效的将机身分量和微动分量分离,提取的三维特征能够较好的反应两种目标微多普勒调制差异,相对于传统方法可以获得更好的分类性能,并且具备噪声鲁棒性,具有较好的推广应用前景。


5 试验结果
5.1 基于仿真数据的分类试验
5.2 基于实测数据的处理结果


6 总 结

