高压水射流数值模拟研究及冲击载荷分析

袁 聪，张培铭，宋锦春

(1.肇庆学院机械与汽车工程学院,广东肇庆 526061； 2.广西机械工业研究院有限责任公司,广西南宁 530000；3.东北大学机械工程与自动化学院,辽宁沈阳 110819)

引言

近年来，随着流体控制技术的发展，高压喷射流在各种除垢除锈的清洗场合的应用变得愈加普遍。高压喷射清洗设备普遍涉及狭小的节流喷嘴，高压流体经过喷嘴产生高速射流，并对喷嘴出口外的物体产生动态负载，冲刷物体表面的结垢或锈迹。为了获得较好的冲洗效果，国内外的学者们开展了各种有益的探索。

HULTI等[1]研究了淹没式喷射流的流场尺寸参数对冲洗效果的影响，揭示了射流冲击载荷与流场的密切相关性。王启博等[2]分析了影响盘式清洗装置清洗效果的主要结构尺寸参数，并对喷嘴布局进行了优化。蔡朋等[3]利用数值流场模拟研究了淹没式喷射流的动态流场及噪声特性。曹泽平等[4]测量了不同参数设置下的环形喷嘴的动态载荷，揭示了靶距对射流冲刷效果的作用规律。王萍辉等[5]根据自振射流的工作原理对喷嘴结构进行了理论分析，对喷嘴的结构参数进行了优化，提供了清洗装置的工作效率及冲刷效果。YANG等[6]通过数值方法研究了不同喷嘴的流场结构，对比分析了喷嘴扩散角度与冲刷效果的关系。FANG等[7]对淹没式水射流进行了大涡模拟，揭示了不同工况条件下的流场结构。蔡腾飞等[8]探讨了喷嘴出口几何尺寸与出口边界层流动特性的关系，并根据分析结果提出了参数优化方案。李玉朵等[9]对某清洗装置的高压喷射流进行了流场数值模拟，并对喷嘴结构进行了优化。

上述研究从多个方面揭示了高速喷射流的流动规律。但是，喷射流的流场结构较为复杂，其与动态冲击载荷的相关性仍需要进一步探索。为此，本研究在OpenFOAM开源CFD平台搭建了面向两相高速喷射流的数值求解器，针对某高压水射流开展数值模拟研究，分析流场结构随工况压差的变化趋势，揭示动态载荷与流场结构的内在关联。

1 数学模型

本研究的研究对象属于雾化喷射，高压喷嘴出口处为压缩气体。喷射流的液核与气体的相互作用将产生散布四周的液滴，随后发生一次雾化，液核在冲击底部靶件后发生剧烈的破碎。这些现象都涉及到液滴间的交互性效应。对此，将通过VOF算法在数值计算中模拟液核及液滴的表面张力，从而对喷射流的雾化过程进行准确描述。

结合相体积守恒定律，可以通过单相的输运方程描述两相流动系统的流相变化规律：

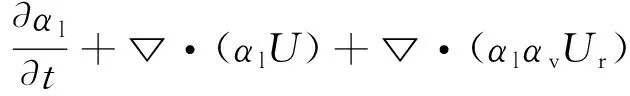
(1)

式中，αl—— 液相体积百分比

αv—— 汽相体积百分比

ρl—— 液相密度

ρv—— 汽相密度

U—— 混相速度

Ur—— 流相间的滑移速率

Ur由如下方程获得：

(2)

式中，cAlpha为界面压缩系数。

混相流体的动量方程为：

(3)

式中，κ—— 界面曲率

σ—— 表面张力系数

τ—— 偏应力张量

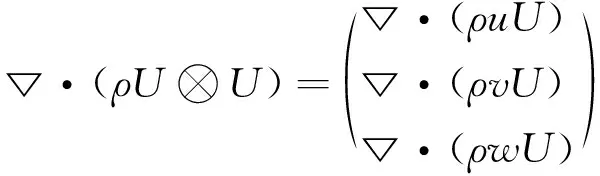
p—— 压力

对动量方程进行半离散，结合速度散度方程，实现速度-压力解耦，获得如下压力方程：

(4)

式中，H(U) —— OpenFOAM的H算子

ap—— 动量方程系数矩阵

上述数学模型的详细推导过程，可参考相关文献[10-11]。

以方孔雾化水射流为算例，对数学模型进行验证。方孔的几何尺寸如图1a所示，网格模型如图1b所示，包含约690万网格单元。文献[12]使用多普勒测速仪(LDV)测量了3个位置的截面时均速度，同时拍摄了出口处的液相轮廓。图2为数值模拟预测的截面速度分布与实验测量的对比，模拟结果预测了方孔左壁面处的回流现象，而且数值模拟结果与实验结果之间的平均偏差约为6%。图3为数值模拟结果预测的瞬时液核雾化轮廓，在喷嘴出口约5 mm处液核轮廓突然扩大，与实验拍摄结果较为吻合。方孔算例表明，该数值方法能够较好地预测小孔雾化喷射流动。

图1 方孔模型

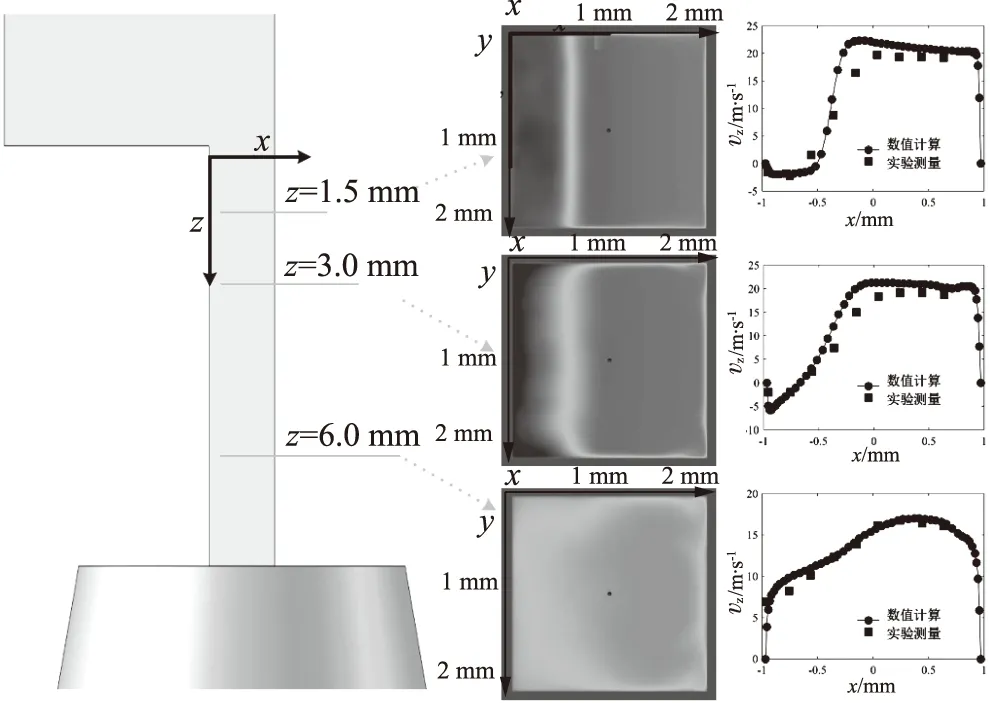
图2 方孔不同截面处的流向速度分布及与实验测量的对比

2 模拟计算设置

使用OpenFOAM较为常用的PIMPLE算法进行时间步推进，相输运方程使用有界性较好的MULES显性算法求解，时间步离散使用二阶精度的backWard策略，对流项使用系数为0.5的Gamma离散策略。入口使用全压力边界条件，入口压力对应3个工况分别为11,31,51 MPa，出口使用非反射边界条件，出口压力均为1 MPa，因此3个工况的压差分别为10,30,50 MPa。其余边界设置为无滑移壁面。流场的几何尺寸如图4a所示，喷嘴的直径为0.3 mm，长度为4 mm，靶距为4 mm。图4b也展示了相应的网格模型，包含约400万网格单元。

图3 方孔喷嘴出口处的雾化轮廓

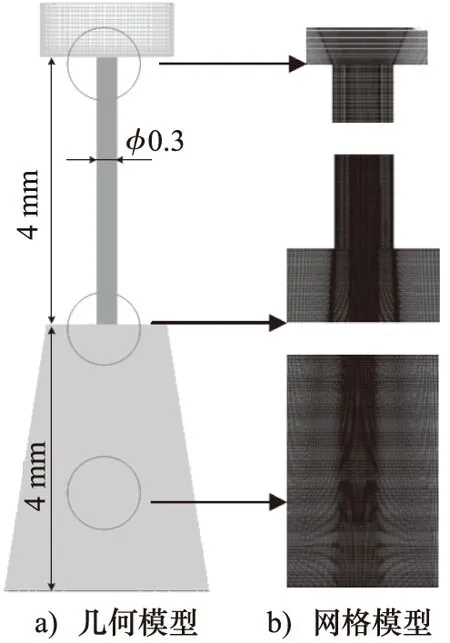
图4 水射流模型

3 模拟结果与分析

图5为各工况的数值模拟结果，上半部分为αl=0.5°的液核形态，下半部分为截面速度分布云图，可以看出，随着压差的提升，液核的表面逐渐变得粗糙，瞬时速度分布呈现愈加强烈的不均匀性。图6为不同工况的瞬时截面液相分布图，其中上半部分为黑色方框的局部放大图。由于喷嘴属于细长孔(直径与长度之比较小)，各工况均可清晰地观察到水力柱塞流现象。图7所示的灰色曲面表示始终被液相占据的区域。图8为根据相关文献[13]的方法推算出的喷雾锥角随压差的变化趋势。压差为10 MPa时，锥角接近0°，说明基本没有发生雾化现象，主要原因在于局部雷诺数较

图5 各工况的整体瞬时流场结构

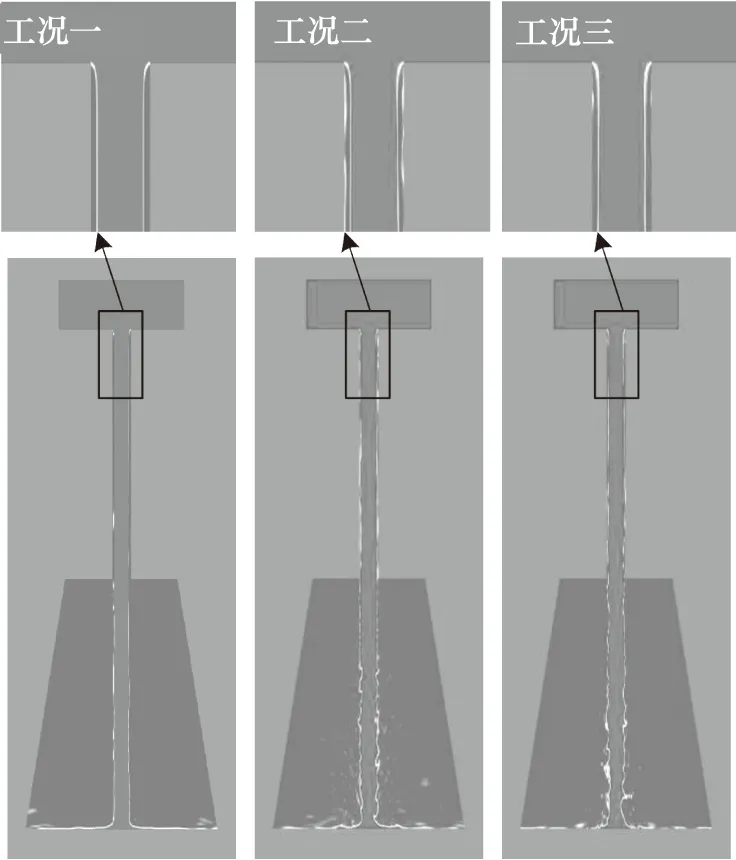
图6 各工况的整体瞬时截面液相分布云图

小，使液核表面并未产生大尺寸的漩涡，从而使液核表面呈现光滑平顺的形态。当压差为30 MPa时，喷雾锥角有大幅度的提升，说明此时已经开始发生雾化现象。如图9所示,上半部分为喷嘴出口外的截面液相云图,下半部分为αl=0.5°的瞬时液核形态，喷射流通过喷嘴出口之后，大量的小液滴从液核剥落，分布在液核的周围。随后，在约1.5 mm的下游区域开始诱发一次雾化现象，尽管液核并未被完全穿透，但液核已产生大尺寸的凹坑，并且这些凹坑具有高度的不规则分布特征。对于工况三，一次雾化起始位置位于喷嘴出口下游1.3 mm处。结合图8可以推测，随着压差的提升，一次雾化的诱发位置越接近喷嘴，从而使喷雾锥角逐渐增大。图10为雾化腔的压力分布云图及Q等值面图。Q准则反映了流场中一个流体微团旋转和变形之间的一种平衡，因此Q等值面可以捕捉流场中的三维漩涡结构。与工况一相比，其余工况都存在2个突出的特点：第一，喷嘴出口处的拟序漩涡迅速瓦解并在下游诱发大量的流向涡；第二，存在明显的压力波现象，说明此时的喷射流属于跨音速流动。这些极端的流场结构是当前研究对象的一次雾化的诱发因素。

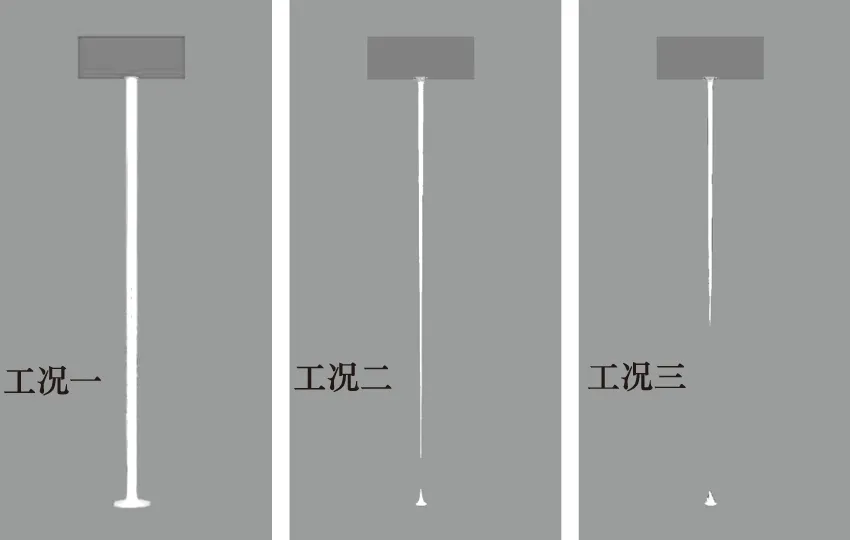
图7 各工况的纯液相区域分布图

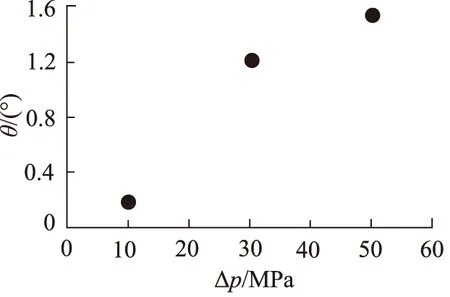
图8 雾化锥角随压差的变化趋势

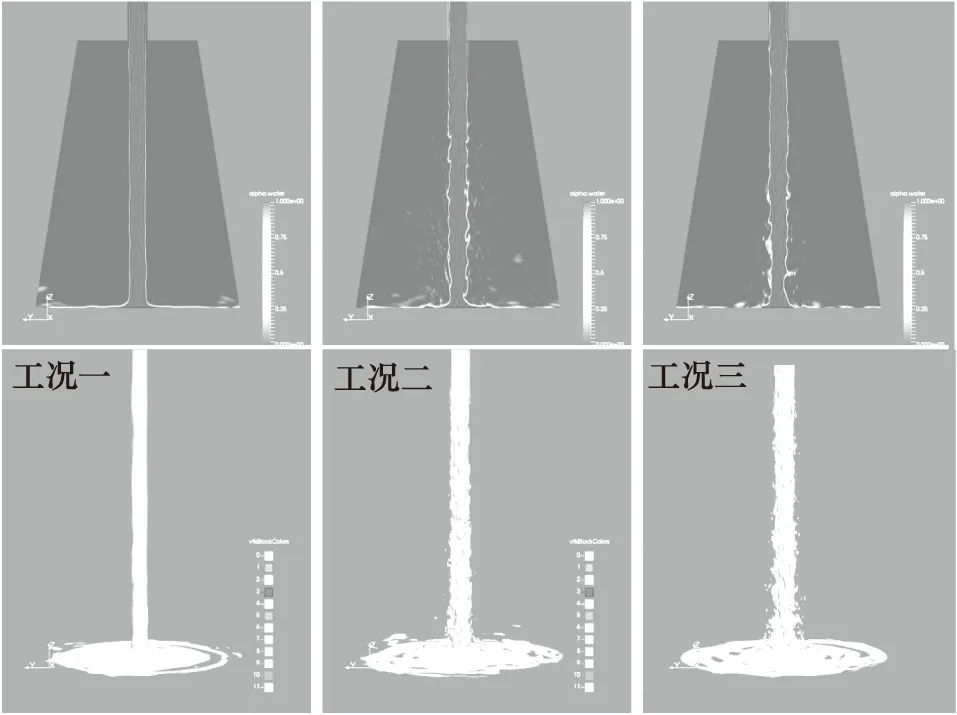
图9 喷嘴出口外的瞬时流场结构

图11为工况一的靶件上方的液核形态及靶件的瞬时压力分布云图。液核保留较完整的圆柱状轮廓，冲击靶件后以较为平稳的状态紧贴靶件表面向四周流动。同时，不同时刻的靶件表面的压力分布变化幅度较小，射流对靶件的总打击力基本保持不变，如图14所示。图12为工况二的靶件上方的液核形态及靶件的瞬时压力分布云图。剧烈的一次雾化效应使液核形态呈现不规则性，在冲击靶件后诱发猛烈的破碎，并在随后的时刻这些破碎的液滴冲击靶件并向四周反射，在靶件表面形成溅射状的雾化现象，造成靶件表面的不均匀压力分布，并且不同时刻的压力分布存在明显差异，在图12(ii)和图13(ii)有较强的瞬时压力峰值，分别高达32.5，54.5 MPa，压力峰值的出现与一次雾化造成的冲击液核的不均匀性有较大的关系。图14为靶件总打击力的时间变化曲线，打击力的波动具有明显的随机特征，其波动幅度较为显著并随着压差逐渐增长，工况一到工况三的总打击力的标准差分别为0.028，0.136，0.517。结合流场结构(图11～图13)可以推测，打击力的随机波动与一次雾化直接相关。一次雾化的作用导致液核的不均匀分布，并且压差越大一次雾化现象愈加强烈，从而导致打击力的波动越大。

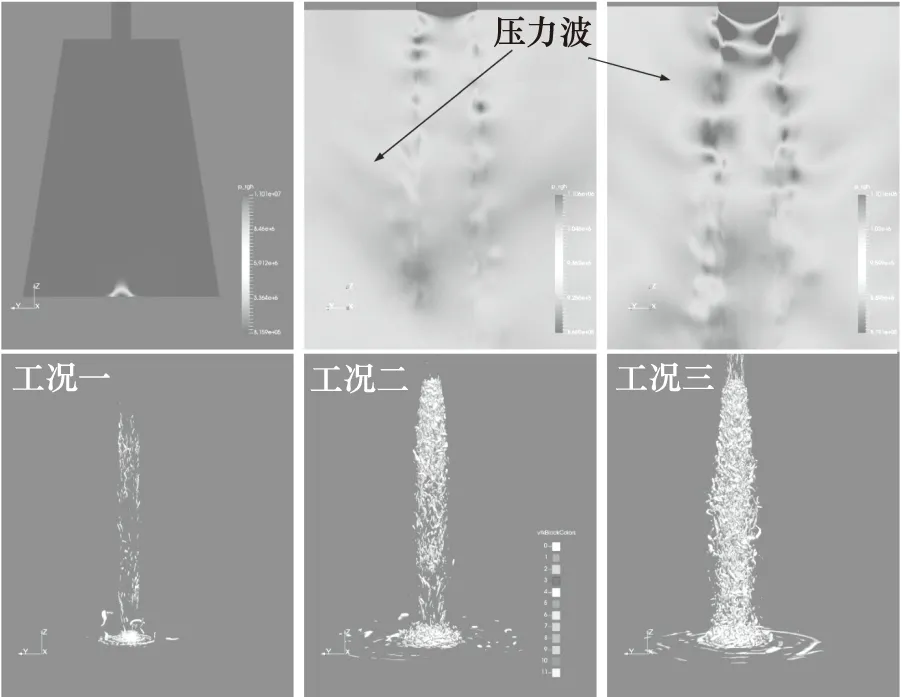
图10 喷射流的压力分布云图及Q=1×1012等值面

图11 工况一的瞬时截面液相云图及靶件表面的压力分布云图

图12 工况二的瞬时截面液相云图及靶件表面的压力分布云图

图13 工况三的瞬时截面液相云图及靶件表面的压力分布云图

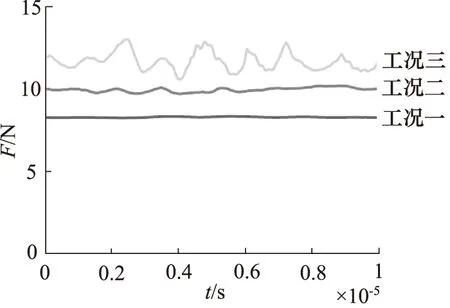
图14 各工况的总打击力时间变化曲线

4 结论

通过对不同压差工况的高速射流开展数值模拟，揭示了重要的流场结构，并获得了以下重要结论：

(1) 当压差为10 MPa时，高速射流与气体的相互作用未对液核产生明显的影响，射流对靶件的冲击作用较为平稳；

(2) 当压差为30 MPa时，高速射流与气体的相互作用诱发一次雾化现象；当压差升至50 MPa时，喷雾锥角从1.3°增长到1.6°，一次雾化现象进一步增强。本研究分析算例的高压射流雾化现象在喷射腔具有2个典型的流场特征结构，分别是大量的流向涡以及压力波。在两者的共同作用下，不断有液滴从液核表面脱落，并逐渐诱发一次雾化现象；

(3) 一次雾化效应使液核呈现不规则的特征，并在靶件表面产生猛烈的破碎，产生局部压力峰值，该压力峰值具有较大的随机性特征，从而强化了液核对靶件的冲击作用，同时打击力随着一次雾化效应呈现明显的波动。当压差从30 MPa提升到50 MPa时，局部压力峰值分别是32.5，54.5 MPa，总打击力波动的标准差从0.136增加到0.517。结果表明，一次雾化效应对高压清洗效果具有促进作用。