重力坝冲沙泄洪闸左导墙抗滑稳定及静动应力分析
彭兆轩,吴 涛,柳 莹
(新疆水利水电规划设计管理局,新疆 乌鲁木齐 830000)
1 研究背景
冲沙泄洪闸的导墙坝段是保证其安全运行的关键受力结构,但是受枢纽布置的限制,导墙坝段的设计尺寸相对较小,常规的钢筋混凝土结构难以保证其正常使用要求,因此极有可能会导致冲沙泄洪闸导墙坝段应力和位移过大,从而影响相邻坝段的整体稳定性。目前,有不少学者通过有限元软件、模型试验、安全监测以及数学模型等方法对导墙坝段进行了大量的分析研究。黄耀华、李振龙等[1-2]应用大型通用有限元软件对溢洪道导墙坝段进行了应力计算,得到了溢洪道导墙坝段及主要部位的大、小主应力,计算结果基本符合实际情况,为导墙设计提供了依据。张忠辉等[3]从巴基斯坦高摩赞大坝枢纽工程实际出发,结合模型试验,探讨了导墙与坝体之间产生流激振的可能性。刘晓平等[4]人以某低水头电站为实例,采用物理模型与数值分析相结合的方法分析了导墙的布置形式对进水口流态的影响,研究表明:随着导墙长度的增加,作用于漩涡的侧推力变大,其形态会随着边界条件的变化而变化。董天松等[5]对某水电站进行了水动力响应测试,同时结合有限元数值分析计算,研究发现在脉动荷载作用下,导墙动应力随高程呈现出先增后减的趋势,在距底部1/3范围内值偏大。关淑萍等[6]根据某水电站导墙坝段长期裂缝监测资料,对导墙裂缝变化规律进行了研究,从而对该水电站导墙坝段做出了安全性评价。程帅、杜占科等[7-8]将简单面上的抗滑稳定有限元分析方法加以改进,推广到复杂的地基面上,结合有限元软件进行了溢洪道导墙的抗滑稳定分析。
本次计算的冲沙泄洪闸左导墙坝段由于受地形和地质条件的限制,右侧溢流堰建基面高程为200.00 m,左侧电站厂房建基面高程为189.00 m,溢流堰建基面与厂房建基面的高差11.00 m。在洪水宣泄期,导墙坝段右侧溢流堰过水而左侧无水,在左右侧建基面高程差及水压力的影响下,导墙坝段与建基面结合处极有可能产生拉裂破坏。因此,对冲沙泄洪闸左导墙坝段进行抗滑稳定及应力分析。
2 工程概况
某水库拦河挡水建筑物为重力坝,正常蓄水位241.00 m,总库容3.25亿m3。枢纽布置从右至左分别为右岸非溢流坝段、右7孔冲沙泄洪闸坝段、右导墙坝段、左5孔冲沙泄洪闸坝段、左导墙坝段、主机间坝段、安装间坝段等共19个坝段。坝顶高程247.00 m,最大坝高58.00 m。左导墙坝段范围为:坝左0+094.50 m—坝左0+124.50 m,坝上0+013.00 m—坝下0+063.50 m。左导墙墙顶高程为247.00 m,最大高度为47.00 m。左导墙既是冲沙泄洪闸的左边墩,又是厂房的右边墙。左导墙坝段在坝下0+017.00 m处设置有结构缝。左五孔设计最大单宽流量达161.00 m2/s,堰面最大流速约为20.00 m/s,属于典型的低水头,大单宽泄量闸坝式水利枢纽。左导墙坝段建基面高程200.00~205.00 m,建基面岩体为弱风化及微风化千枚岩。
导墙左右侧建基面高差11.00 m,在洪水宣泄期时,右侧过水而左侧无水,容易造成右侧溢流堰建基面拉裂破坏。导墙上游侧建基面高出下游侧建基面5.00 m,在设计洪水位工况时,上下游水位仅相差1.00 m且导墙上下游侧建基面高程不一致,将会造成导墙下游侧扬压力水头高于上游侧的情况,极有可能会致使导墙失稳。
3 有限元计算
3.1 计算方法简介(1)抗滑稳定计算方法。水利工程中分析导墙坝段抗滑稳定的主要方法与重力坝的抗滑稳定计算方法相似,大都采用刚体极限平衡法、有限元法和地质模型试验法,在水工计算中常采用前两种计算方法[9-13]。依据《混凝土重力坝设计规范》(SL 319-2018)[14],在基本荷载组合和特殊荷载组合下运用刚体极限平衡法进行抗滑稳定计算。
(2)动应力计算方法。对于地震工况,采用振型分解反应谱法对左导墙坝段进行动力分析计算。因为要在提高计算精确度的前提下而又不增大计算量,所以本次计算采用了结构前30阶自振频率及各阶振型。运用ABAQUS程序进行反应谱分析时,对于结构受到单向激励作用情况,先计算出各阶模态响应及其参与系数,然后在各阶模态响应的基础上,采用不同的组合方法进行叠加,得到结构的总响应[15]。本次关于水平向地震作用的组合计算采用完全二次型方根法。大坝-水动力相互作用采用附加质量法,结构和地基间的动力相互作用和地震动的输入,采用无质量地基底部均匀输入方式[16]。进行地震工况计算时,总的应力计算结果按“静应力+动应力”组合方式来进行提取。
3.2 计算工况左导墙坝段抗滑稳定及应力由运行期的设计洪水和校核洪水两种工况控制,故应分别按基本组合和特殊组合设计,计算工况及荷载组合见表1。

表1 左导墙坝段计算工况及荷载组合
3.3 计算模型及典型断面利用大型有限元分析软件ABAQUS对左导墙完整坝段及地基进行三维实体建模。左导墙坝段无强风化岩层,弱风化带厚0~2.33 m,弱风化底板高程一般在200.00 m,建基面以下约20.00 m处有一条由右岸倾向左岸的断裂带。根据一般工程经验及本工程实际地质条件,计算模型基础的选取范围考虑为结构尺寸的1~2倍。有限元模型取导墙完整坝段,地基深度为87.00 m,深入断裂带以下约67.00 m;左侧地基为56.00 m、溢流堰右侧地基为66.00 m;导墙上、下游侧的地基长度为88.50 m,选取范围约为导墙结构尺寸的1.5倍。计算模型基本采用八节点六面体单元,由于导墙内部灌浆排水廊道错综复杂,划分网格难度较大,所以局部过渡区域采用四面体单元,共62 116个节点,40 966个单元。冲沙泄洪闸左导墙三维有限元模型网格剖分如图1所示。三维有限元模型采用笛卡尔直角坐标系,X轴方向为坝轴向,从右岸指向左岸为正向;Y轴方向为顺河向,从下游指向上游为正向;Z轴方向为竖向,沿坝高方向从下向上为正向。
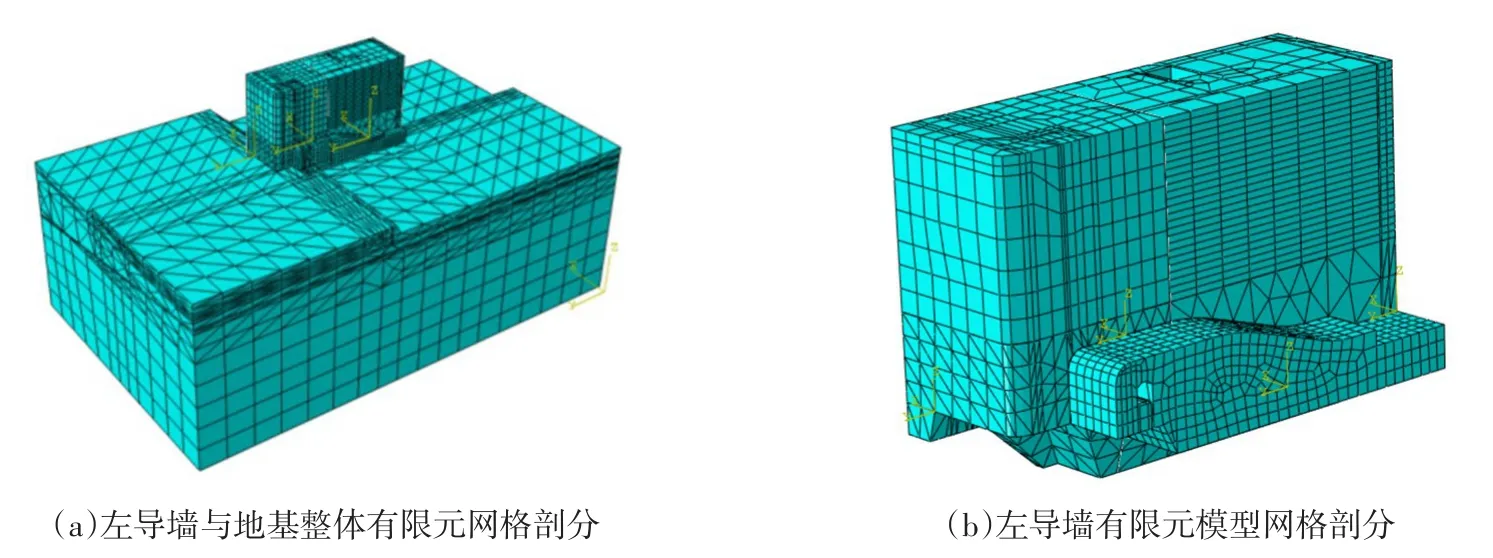
图1 冲沙泄洪闸左导墙有限元模型网格剖分
为有效实施左导墙坝段的渗流、抗滑稳定及应力计算,应合理选取左导墙坝段的典型纵、横断面。综合考虑左导墙坝段的灌浆排水廊道、坝基防渗帷幕和排水孔幕等结构布置特征,本次计算拟选取4个典型纵断面及7个典型横断面,如图2和图3所示。其中,左导墙坝段的典型纵断面包括坝左0+099.00(左导墙坝段与冲沙泄洪闸闸堰衔接处)、坝左0+096.75(溢流堰坝段中心线)、坝左0+103.50(纵向灌浆排水廊道中心线)和坝左0+112.00(左导墙坝段中间部位)共4个纵断面;左导墙坝段的典型横断面包括坝上0+010.00(左导墙坝段上游头部)、坝上0+006.50(横向灌浆排水廊道中心线)、坝下0+005.80(建基面折坡点)、坝下0+015.25(交通排水廊道中心线)、坝下0+020.00(左导墙坝段结构缝附近)、坝下0+049.00(溢流堰台阶处)和坝下0+056.00(溢流堰台阶中间部位)共7个横断面。

图2 左导墙各典型纵、横断面平面位置示意图

图3 左导墙各典型横断面示意图
3.4 边界条件及计算假定左导墙坝段主体与地基接触面按弹塑性考虑,其他方向均为自由变形,不考虑约束。在选定的地基范围内,四周约束水平移动(即滚轴支座),底部施加固定约束(即固定支座)。
本次对冲沙泄洪闸左导墙坝段的有限元分析作如下基本假定:(1)材料的密度、弹性模量、泊松比以及渗透系数等参数假定为各向同性。(2)坝体混凝土和微风化岩体按线弹性模型考虑,坝基接触面按弹塑性模型考虑。(3)考虑到左导墙坝段与相邻坝段间均设置伸缩缝,不计相邻坝段的影响。(4)三维动力有限元计算时,主要计算假定:结构物的地震响应是弹性的,采用叠加原理进行振型组合;结构物各支撑处的地震动完全相同,基础与地基无相互作用;地震动过程是平稳随机过程。将动水压力对坝体地震反应的影响用等效的附加质量考虑,与坝体质量相叠加来进行动力分析。因此计算时将地震动水压力转化为相应的坝面附加质量进行分析,其基本计算假定为:水是可压缩的;地面运动为水平简谐运动;大坝迎水面铅直,库底水平。
3.5 计算参数冲沙泄洪闸左导墙坝段三维有限元渗流分析、抗滑稳定分析以及应力分析,计算所需的左导墙坝段及地基的渗透系数见表2,冲沙泄洪闸左导墙坝段各分区混凝土、锚索以及坝基岩体的物理力学参数见表3。

表2 左导墙坝段及地基的渗透系数 (单位:cm/s)

表3 左导墙各分区混凝土、锚索及坝基岩体物理力学参数
水利工程中土与刚性结构之间没有过渡体,由于两种接触材料物理力学性质差异较大,外部荷载作用往往会使接触面两侧结构产生较大的变形差异,并且数值模拟时在接触面处往往会产生比实际更大的剪应力,导致计算结果误差较大,因此在两种结构接触面上采用接触单元进行过渡,以得到更准确合理的计算结果。目前常采用的是无厚度Goodman单元,该单元物理意义明确且无厚度,可以较好的反映材料性质差异较大的两种结构接触面上的张裂和相对滑动。其本构关系为:

式中:Wx、Wn分别为接触面切向及法向相对滑移量;Ks、Kn分别为切向及法向劲度系数。
由于Goodman接触单元无厚度,接触面两侧单元易发生嵌入和脱离,为解决这一现象,当接触面受压时,Kn取大值,当接触面受拉时,Kn取小值;Ks通过双曲线拟合常规直剪试验得到的不同应力应变关系求得,可根据式(2)确定:

式中:K、Rf、n为非线性指标,由直剪试验确定;δ为接触面摩擦角;Pa为标准大气压;γw为水容重。
混凝土与坝基岩体属于两种物理力学性质差异较大的材料,若不考虑接触,则导致计算的应力产生较大误差,与实际情况不符。因此,冲沙泄洪闸左导墙坝段与基岩接触面采用Goodman接触面单元考虑其不连续变形特性,接触面模型参数参照类似工程经验选取,见表4。

表4 Goodman接触面模型参数
4 有限元计算结果分析
4.1 渗流计算结果分析通过对左导墙坝段的三维有限元渗流计算,得出了正常蓄水位工况、设计洪水位工况和校核洪水位工况下导墙坝段与建基面结合处扬压力水头的分布情况,如图4—图6所示。典型纵断面在建基面处的扬压力水头分布图上,桩号以坝上为负,坝下为正,分布图中的扬压力水头以建基面为基准。

图4 正常蓄水位工况典型纵断面在建基面处的扬压力水头分布

图5 设计洪水位工况典型纵断面在建基面处的扬压力水头分布

图6 校核洪水位工况典型纵断面在建基面处的扬压力水头分布
根据图4—图6可知,不同工况下各典型纵断面在建基面处的扬压力水头分布规律具有相似性,顺河向扬压力水头总体呈先减小后增大的趋势,即左导墙坝段扬压力水头呈上下游坝段高、中间坝段低的分布特征。结果表明,通过设置防渗帷幕及排水孔幕以降低扬压力的作用较明显。在正常蓄水位工况下,上下游水位差较大,因此下游扬压力水头低于上游扬压力水头;在设计洪水位和校核洪水位工况下,上下游水位差小于1.00 m,同时左导墙坝段的上下游侧地基不平整,上游侧地基较下游侧地基高出5.00 m以上。因此,计算结果中出现下游扬压力水头大于上游扬压力水头的情况。
4.2 抗滑稳定计算结果分析基于左导墙各典型纵断面渗流计算结果,运用刚体极限平衡法分别进行非地震工况和地震工况下左导墙各典型纵断面以及导墙整体的抗滑稳定分析。
通过对不同工况下左导墙坝段顺河向抗滑稳定计算结果的分析与整理,得出了各典型纵断面抗滑稳定安全系数的分布规律,最不利的抗滑稳定计算结果汇总见表5。
根据抗滑稳定控制标准,在基本荷载组合下,抗滑稳定安全系数K不应小于1.05,K′不应小于3.0;在特殊荷载组合下,抗滑稳定安全系数K不应小于1.0,K′不应小于2.5(地震工况不小于2.3);抗剪摩擦系数f为0.5,抗剪断摩擦系数f′为0.8,C′为600 kPa。由表5可知,典型纵断面抗滑稳定安全系数的最小值均分布在坝左0+099.00(左导墙坝段与冲沙泄洪闸闸堰衔接处)。在上述4种工况下,各典型纵断面及导墙整体坝段抗滑稳定安全系数最小值均符合规范要求,因此左导墙坝段满足顺河向的抗滑稳定。这说明导墙上下游侧建基面高程差并没有对其顺河向的抗滑稳定造成太大的影响,该设计方案合理可行。

表5 左导墙坝段顺河向最不利的抗滑稳定计算结果汇总
4.3 应力分析(1)非地震工况应力分析。针对左导墙坝段三维有限元模型,进行了非地震工况下的应力有限元计算,计算结果表明,非地震工况左导墙及基岩的变形较小(一般仅为毫米级)、拉应力区宽度及拉压应力均符合规范要求。正常蓄水位工况、设计工况和校核工况下导墙建基面应力分布规律基本一致,以正常蓄水位工况为例,导墙建基面σx、σz和τxz在各典型纵断面处的应力分布情况如图7—图9所示。

图7 正常蓄水位工况建基面沿坝轴向应力σx

图8 正常蓄水位工况建基面上竖向应力σz

图9 正常蓄水位工况建基面上竖向剪应力τxz
由图7—图9可知,在正常蓄水位工况下,建基面沿坝轴向最大拉应力为1197.29 kPa,发生在坝左 0+099.00、坝下 0+020.00 处;竖向最大压应力为-9607.98 kPa,发生在坝左 0+124.50、坝下 0+015.25处;最大剪应力为1115.12 kPa,发生在坝左0+124.50、坝下0+015.25处。设计洪水位工况和校核洪水位工况下,建基面沿坝轴向、竖向正应力和剪应力分布规律与正常蓄水位工况类似。各工况左导墙坝段建基面最大拉、压应力及竖向最大拉应力区宽度汇总分别见表6和表7。
由表6可知,正常蓄水位工况、设计洪水位工况和校核洪水位工况下建基面坝轴向最大拉应力分别为1197.29 kPa、1259.73 kPa和1316.95 kPa。左导墙坝段采用不同标号的混凝土分区浇筑,导墙与建基面结合部位由C20混凝土浇筑完成。根据应力控制标准,坝轴向最大拉应力均超出C20混凝土轴向抗拉强度设计值1.1 MPa,在洪水宣泄期极有可能导致左导墙坝段与建基面结合处受拉破坏,形成裂缝。因此,根据本次计算结果,建议在结构设计与配筋计算时,进行强度复核。竖向最大拉应力、最大压应力以及最大剪应力均符合地基承载力要求。

表6 各工况左导墙坝段建基面应力计算结果汇总 (单位:kPa)

表7 各工况左导墙建基面竖向最大拉应力区宽度及其与断面宽度的比值
根据《混凝土重力坝设计规范》(SL 319-2018)的要求,采用线弹性有限元法计算的坝基应力,其坝踵部位垂直拉应力区宽度,宜小于坝踵至帷幕中心线的距离且宜小于坝底宽度的0.07倍。由表7可知,正常蓄水位工况、设计洪水位工况和校核洪水位工况下建基面竖向最大拉应力区均发生在坝左0+099.00处,最大拉应力区宽度与断面宽度的比值均小于坝踵至帷幕中心线的距离且小于所在断面宽度的0.07倍,符合建基面竖向拉应力控制标准。
(2)地震工况应力分析。根据《水工建筑物抗震设计规范》(GB 51247-2018)[17]规定,对于工程抗震设防等级为乙类,设计烈度小于8度且坝高不大于70m的重力坝抗震计算,一般只考虑顺河流方向的水平地震作用。结果表明,地震工况下左导墙坝段及基岩的变形很小(一般为10~30 mm),基本属于正常范围。故选择各典型纵断面上的应力分布尤其是建基面应力分布情况作为应力计算结果分析的重点,应力计算结果按“静应力+动应力”组合方式来提取。地震工况左导墙坝段建基面动应力分布情况如图10—图12所示。
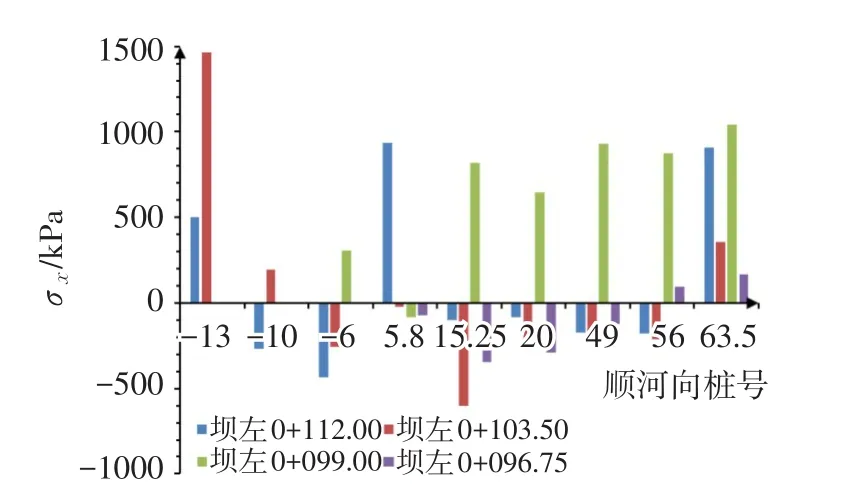
图10 地震工况左导墙坝段建基面沿坝轴向应力σx

图11 地震工况左导墙坝段建基面竖向应力σz

图12 地震工况左导墙坝段建基面竖向剪应力τxz
由图10—图12可知,地震工况下左导墙坝段建基面沿坝轴向和竖向最大拉应力分别为1462.39 kPa和1170.22 kPa,均发生在坝左0+103.50、坝上0+013.00处。根据应力控制标准,坝轴向和竖向最大拉应力均大于C20混凝土轴向抗拉强度设计值1.1 MPa,因此坝轴向最大拉应力与竖向最大拉应力均不满足强度要求,需进一步进行结构优化设计。左导墙坝段建基面最大剪应力1060.54 kPa,发生在坝左0+103.50、坝上0+13.00处,满足C20混凝土抗剪强度设计值1.76 MPa的要求。地震工况典型纵断面竖向最大拉应力区宽度汇总见表8。

表8 地震工况典型纵断面竖向拉应力区宽度及其与断面宽度的比值
根据表8可知,地震工况下左导墙坝段建基面竖向最大拉力区发生在坝左0+099.00处,其与断面宽度的比值均小于0.07,满足应力控制指标。这一位置与非地震工况导墙坝段建基面竖向最大拉应力区发生的位置相同,说明纵断面坝左0+099.00(左导墙坝段与冲沙泄洪闸闸堰衔接处)为导墙结构薄弱面,在设计施工时应着重考虑其安全性。
5 结论和建议
通过对冲沙泄洪闸左导墙坝段在4种不同工况下的的抗滑稳定和应力有限元分析,得出以下结论:
(1)左导墙坝段各典型纵断面在建基面处的扬压力水头分布规律具有明显的相似性。总体来看,导墙坝段建基面处扬压力呈现出上下游坝段高,中间坝段低的分布特征。
(2)左导墙坝段典型纵断面抗滑稳定安全系数最小值均发生在坝左0+099.00处,且各纵断面及导墙整体坝段均满足顺河向的抗滑稳定。
(3)非地震工况和地震工况建基面沿坝轴向最大拉应力均超出其轴心抗拉强度设计值,不满足强度要求。
导墙左右侧建基面高差11.00 m,在洪水宣泄期造成了建基面处混凝土拉裂破坏,对导墙的正常运行造成了极大的安全隐患,建议下阶段进一步进行导墙结构与配筋的优化设计。导墙上下游建基面的高程差,虽增大了基底扬压力,但并没有对其顺河向稳定造成太大的影响。
本文计算时,未考虑导墙坝段与左侧电站厂房坝段在自重及水压力等荷载作用下是否会接触的情况,在下阶段将会着重考虑并分析两坝段在各工况下的接触状况以及导墙的侧向抗滑稳定。

