航线维修任务人力资源多目标优化模型研究

贾宝惠，唐庭均，卢 翔

(中国民航大学航空工程学院，天津 300300)

随着飞机维修支援活动中不断引入系统工程思想，综合保障分析(logistics support analysis，LSA)开始在民机产品四性与支援工程中扮演重要角色。20世纪60年代，美国就有了综合后勤保障的概念。2000年，Taylor[1]针对当前快速发展的航空业，建立了一种新的模型，能够评估维修资源的管理计划，实现了航空公司根据成本效益制定维修人员数量的计划。2006年，Guarnieri等[2]针对飞机受可用后勤资源制约问题，提出了在给定的时间间隔内能够飞机正常工作所需后勤资源的模型。2009年，Firat等[3]提出了一种面向维修任务的多技能人员配置模型，证明了混合整数规划模型对这类问题的求解优势。2015年，Manzini等[4]提出了一个非线性模型，使预防性维修和纠正性维修的成本以及技术人员的工作量和备件成本降到最低。

S3000L是欧洲宇航与防务工业协会(Aerospace and Defence Industries Association of Europe，ASD)在总结多年飞机维修工程分析经验的基础上，联合飞机主制造商形成的国际规范。权衡飞机维修过程中的经济与时间因素，合理配置维修人员，对飞机维修任务中维修人员配置具有重大意义。2015年，夏哲[5]通过研究S3000L在民用飞机领域的应用，提出了分析维修资源需求的指导方法。2006年，金星[6]通过分析装备维修保障资源，并运用基本遗传算法建立装备维修保障资源模型。2007年，杨光辉[7]以排队论为基础建立了维修人员的配置模型。2010年，艾宝利等[8]对模拟退火遗传算法进行改进，优化了装备维修资源的分配。2013年，谷玉波等[9]对维修人员进行定性分析，将其分类，并运用遍历法建立维修人员配置模型；李连等[10]以排队论为基础对可修航材进行了预测。

目前，关于航线维修任务人员配置方案的研究较少。为此，提出航线维修人员配置的方法，以排队论为基础建立以最小维修成本、最小维修时间与最大化可用度为目标的多目标优化模型，通过非支配排序遗传算法(non-dominated sorting genetic algorithm，NSGA Ⅱ)求解该模型，为航线维修人员配置提供理论参考。

1 模型输入

航线维修任务可以定义为一个排队系统，该系统的顾客是维修任务，服务机构是维修人员。

为确定排队系统的关键指标，需要大量的数据。但是由于统计工作量大，一般人士也很难统计出某一时段内的真实数据情况，而且何奕军在关于航线维修人力资源优化配置的研究中已经做过统计[11]，因此直接参考其统计数据，进而计算出顾客与服务台的输入分布。

1.1 维修任务到达概率分布

某飞机维修基地的每日维修任务数量分布如表1所示。

表1 每日维修任务数量Table 1 Number of daily maintenance tasks

由于航线维修任务产生是随机事件，假定其满足泊松分布。为观察该分布规律是否满足泊松分布的条件，用χ2检验法进行验证，得到单位时间内到达的维修项目符合泊松分布的拟合检验(表2)。

表2 维修任务拟合检验Table 2 Fitting test of maintenance task

1.2 维修服务时间分布

某维修基地的维修时间统计如表3所示。

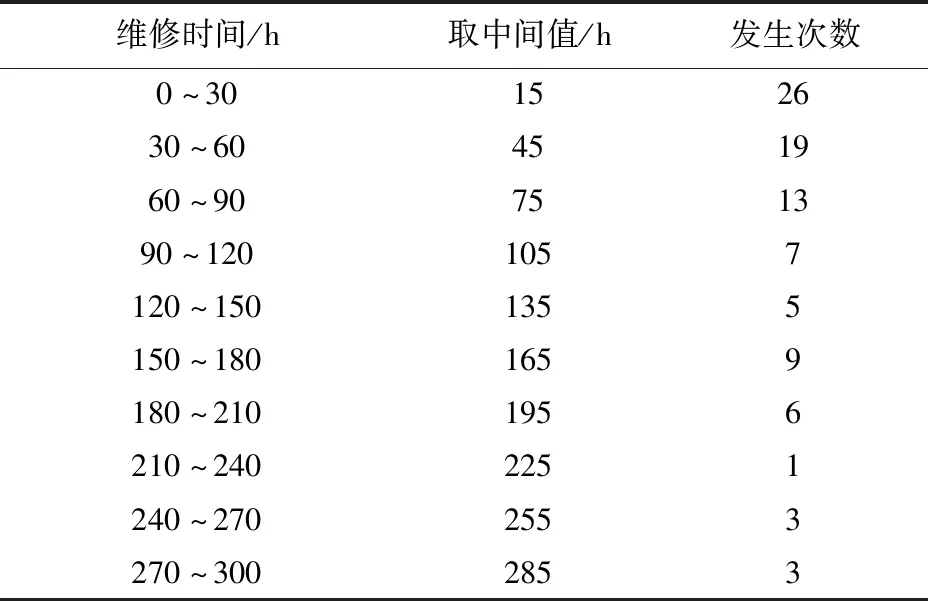
表3 某基地维修时间统计Table 3 Maintenance time statistics of a maintenance base

每架飞机的平均维修时间为

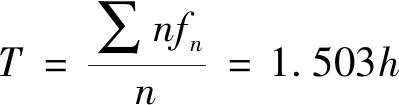
(1)

式(1)中：n表示故障的数量；fn表示故障数量为n的发生次数。

平均服务率为μ，则单位时间内服务完的飞机架次为

(2)

表4 维修时间拟合检验Table 4 Fitting test of maintenance time

2 基础模型建立

2.1 特征描述

航线维修排队系统模型结构如图1所示。

图1 航线维修排队系统Fig.1 Queuing system of route maintenance

从图1可以看出，随机服务系统由输入过程、排队规则和服务机构3部分组成。为了便于研究问题，对模型定义如下。

(1)顾客源：维修任务无限，到达随机、相互独立。

(2)到达类型：根据上文对维修任务的概率分布的判断，确定维修任务到达是服从泊松分布的。

(3)排队规则：故障飞机需要等待维修组完成维修任务，且维修组有空闲，否则必须排队等待，所以是等待制。

(4)服务方式：根据上文对服务时间的概率分布的判断，确定维修时间服从负指数分布。

(5)服务机构：以维修组为单位，每个维修组有一名放行人员和三名维修勤务人员，并假设每个维修组维修能力相同。

综上所述，航线维修任务的排队系统的定义为：具有多个服务台，多个服务台同时服务，且服务台之间是并联的。

2.2 基于M/M/C的排队模型建立

根据分析建立M/M/C排队模型，规定服务台的维修效率相同，不同的服务台之间相互独立。图2为航线维修任务排队模型的状态转移图。图2中，λ为飞机故障的平均到达率；μ为平均服务率，即维修组的平均工作能力；整个服务系统的平均服务能力为cμ，c表示维修台的数量；规定各服务台是相互独立的，并且平均服务速率相同，即μ1=μ2=…=μn；ρ为系统的平均利用率，ρ=λ/cμ，只有当ρ<1时，平稳分布才能存在。

根据图2的稳态状态转移图，可以得出状态方程为

图2 航线维修状态转移图Fig.2 State transition diagram of route maintenance

(3)

采用递推法求解式(3)可得

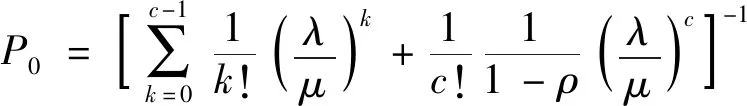
(4)

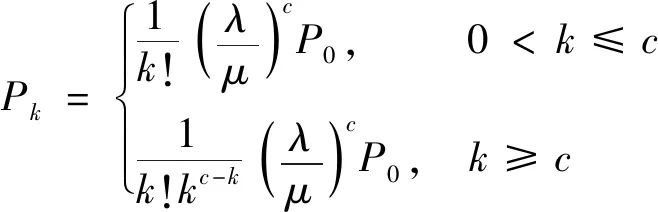
(5)

式中：P0表示所有维修组没有工作的概率；Pk表示有k个维修组在工作的概率，如果Pk过大，则表示维修人员过多，虽然会提高维修的效率，但会造成人员过剩[12]。

进而可以求出模型的关键运行指标。

(1)维修基地内故障飞机的待修项目排队长度为

(6)

(2)平均队长，即所有的维修任务数量之和，表示为

Ls=Lq+cρ

(7)

(3)故障飞机在等待维修与维修过程的时间之和为

(8)

(4)故障飞机在等待维修服务之前的等待时间为

(9)

取λ=0.95个/h，μ=0.14个/h。当航线维修系统进入稳态时，可以根据式(4)～式(8)求出其关键的运行指标，得到的运行指标数据如表5所示。

由表5可知，随着维修组数量的增加，维修任务中的排队队长在减小，故障在排队系统中的逗留时间也在减少，但维修组空闲的概率也在增加；随着维修组的增加，系统逐渐进入稳态，但会造成维修人员的浪费。

表5 运行指标计算结果Table 5 Calculation results of operation indexes

通过前文的分析计算，可以得到航线维修任务排队系统的重要指标：Ls和Ws。利用式(6)～式(9)计算出不同维修组数量下对应的Ls、Ws，再对其增加必要的约束条件就可以确定维修组的合理的数量。但上述排队论的基本模型只能计算出航线维修排队系统中的服务时间以及排队队长等基础指标，不能够确定航线维修维修组的数量，故需要建立航线维修优化模型。

3 人力资源多目标优化模型建立

航线维修人力资源配置的优化实际可以转化为航线维修任务中的维修组的数量的优化，是指在保证有较高的设备可用度的前提下，通过合理配置维修组的数量，提高航线维修任务中的人员的利用率。通过基本的排队论模型只能够确定系统达到稳态时的人员数量，无法应用于实际当中。因此，采用多目标优化的方法，综合考虑航线维修中的维修成本、维修时间以及可用度来优化维修组的数量。

3.1 维修成本

航线维修任务的维修费用来自两个方面，一是服务台的费用，即维修人员的工资；二是维修任务在排队系统逗留付出的费用，即飞机停场费用。

在建立的排队论模型的基础上，建立维修费用模型，如式(9)所示：

C=CscWs(1-P0)+CwLsWs

(10)

式(10)中：C为维修费用；Cs表示维修组单位时间成本，即维修人员的工资；Cw表示每个维修任务单位时间的费用。

3.2 维修时间

在航线维修任务中，Ws为维修任务在排队系统中的总的逗留时间，可以作为航线维修时间，维修时间模型为

E=Ws

(11)

3.3 设备可用度

在民机维修任务过程中，需要分析飞机的系统特性，而可用度是系统的主要特性之一，通过对飞机可用度进行分析，可以在保证维修效率的同时，使飞机具有较高的可用度。故引入了设备可用度模型：

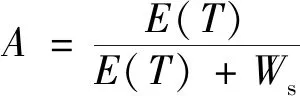
(12)

式(12)中：A表示系统的使用可用度；E(T)表示故障平均间隔时间，E(T)=1/λ。

3.4 多目标模型

通过分析单一目标无法求出航线维修维修组配置的最优解，需要将单目标问题转换为多目标问题[13]。在建立了航线维修排队模型的基础上，建立以最小化维修费用、最大化设备可用度与最小化维修时间的多目标优化模型：

(13)

式(13)中：为确保排队系统能够进入稳态，需保证ρ<1，故c≥8。

4 多目标模型求解

带精英策略的NSGA Ⅱ是在非支配排序遗传算法(non-dominated sorting genetic algorithm，NSGA)的基础上改进而来的。利用NSGA II算法求解中的多目标模型的步骤如下。

(1)初始化程序；计算各目标函数值。

(2)通过非支配排序方法排序并计算每一层的拥挤度。

(3)通过精英选择策略，从当前种群中挑选出Ppop/2优势个体作为父代种群(Ppop为种群数量)。

(4)通过选择、交叉、变异操作，生成Ppop/2个子代种群，并计算其目标函数值。

(5)将父代与子代种群结合，并利用层次聚类法挑选出Ppop/2个个体。

(6)判断终止条件，如果迭代次数达到最大进化代数，则进入步骤(7)，否则进入步骤(3)循环。

(7)选择出最优解[14]。

NSGA Ⅱ算法流程图如图3所示。

图3 NSGA Ⅱ算法流程图Fig.3 Flow chart of NSGA Ⅱ

5 实例分析

5.1 模型求解

从文献[11]可以得到：Cs为维修组单位时间内的成本，取Cs=480 元/(h·人)，假设每个维修组有4人，所以应该取Cs=1 920元/(h·人)；取Cw=4 167 元。

在求解算法中，设种群数量Ppop=20，迭代次数G=100，初始变异率pm=0.1，初始交叉率pc=0.1。随着遗传进化的过程，维修成本、维修时间与可用度的迭代过程如图4所示，得到Pareto最优解集如图5所示，生成Pareto最优解如表6所示。

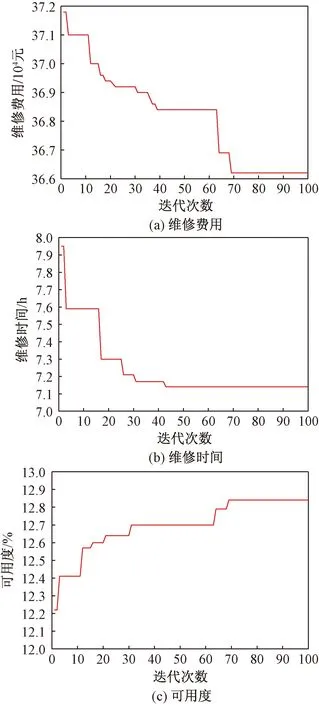
图4 迭代曲线Fig.4 Iterative curve

图5 Pareto最优解集Fig.5 Pareto optimal solution set

从表6可以看出，算法的最终结果生成一个Pareto最优解集，随着维修组数量的增加，维修成本与可用度上升，维修时间减少，所以不能直接判断出最优的维修组数量，需要通过一定的方法计算出最优值。

由于3个目标函数的值差距特别大，维修成本较大，而可用度只是不到1的小数，因此不能用线性加权的方法求出最优解，采用中心加权的方法建立最优解函数，如式(14)所示：

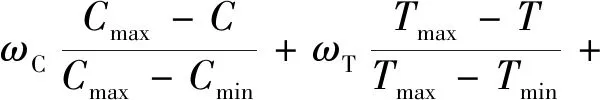
(14)

式(14)中：ωC、ωT、ωA分别为目标C、T、A的权重，取0.4、0.4、0.2；Cmax、Cmin分别为目标C的最大值与最小值；Tmax、Tmin分别为目标T的最大值与最小值；Amax、Amin分别为目标A的最大值与最小值。

将表6中的Pareto最优解代入式(14)中得到结果如表7所示。

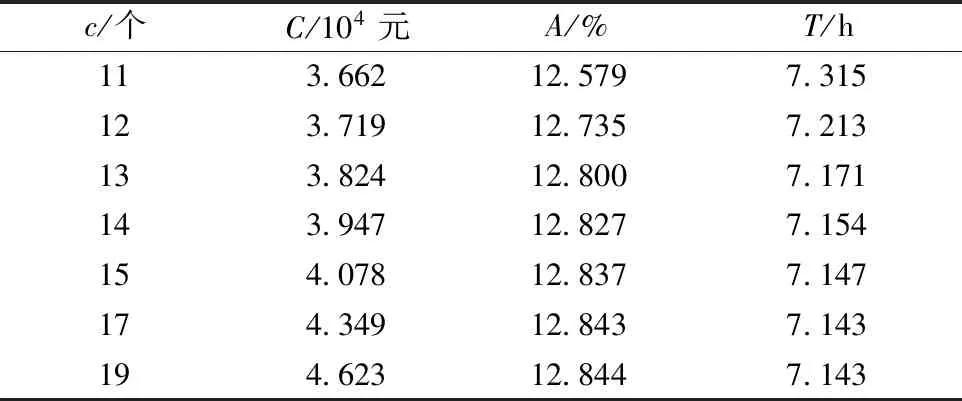
表6 Pareto最优解集Table 6 Pareto optimal solution set

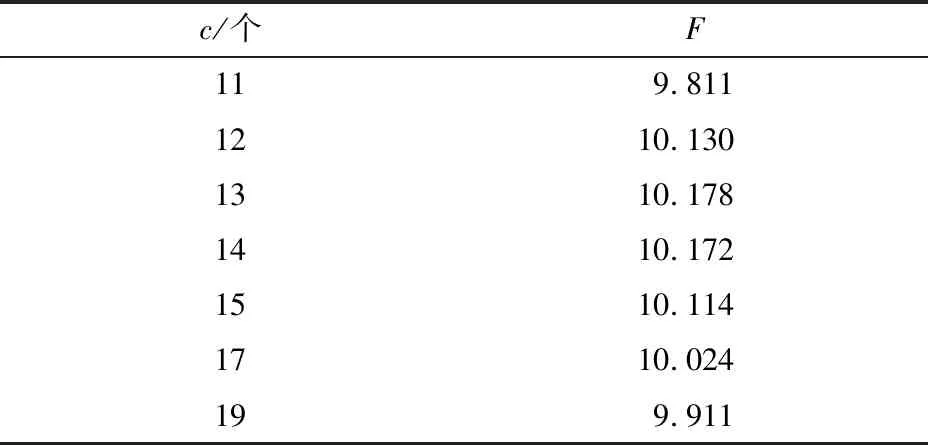
表7 计算结果Table 7 Calculation result

从表7可以看出，维修组数量为11时，目标函数的值最少，故取维修组的数量为11，能够得到最优结果。

5.2 优化结果分析

为了验证上述优化模型是否有效，采用该模型优化某公司的人员配置。该公司维修系统共有一线维修人员16人，分成4个维修组轮流值班，根据该公司统计，平均维修任务到达率为0.2个/h，平均维修效率为0.16个/h。根据多目标优化模型可以计算得到理论配置方案，当取维修组数量为5，结果最优，将其与实际配置进行对比，结果如表8所示。

从表8可以看出，在新的维修组配置方案下，航线维修系统各方面的性能参数都有了不同程度的提高。证明了多目标优化模型对航线维修维修组配置的有效性。

表8 优化目标函数对比Table 8 Comparison between optimization results

6 结论

建立了基于排队论的航线维修人力资源多目标配置模型，并通过NSGA Ⅱ算法求解。得出以下结论。

(1)排队论方法可以应用到航线维修维修组数量确定模型的建立。

(2)排队论模型只能够得到基础的指标，通过引入成本、时间与可用度指标建立多目标模型，能够确定最优维修组数量。

(3)通过NSGA Ⅱ算法求解多目标优化模型，证明了该算法的有效性。