随钻声波测井中消除钻铤直达波方法的研究与验证

张泽阳，法 林

(西安邮电大学电子工程学院，西安 710121)

随钻声波测井的最主要目的是准确测量水平井和大斜度井地层的纵波和横波速度，分析采集数据获得地层岩石的物理性质和油气资源信息，从而提高油气产量[1]。但是沿着钻铤传播的直达波严重干扰地层波信号的测量。目前，常规随钻声波测井仪主要采用无源噪声控制技术，就是在井下仪器外壳通过周期性刻槽、变径组合隔声和震电效应等方法来达到隔声的目的[2]。但是在随钻声波测井工程中，测井仪通常被放置在钻铤中，如果对钻铤进行周期性刻槽或变径隔声，需要对钻铤进行适当加工，就会降低钻铤机械强度，导致测井风险增大。由于钻铤尺寸和刻槽深度限制，隔声阻带带宽有限，也无法隔离低频率的钻铤直达波对地层波信号的干扰。同时震电效应隔声还处在理论研究阶段，尚未应用于实际测井[3]。

为此，提出一种利用自适应有源噪声控制技术(active noise control，ANC)达到消除钻铤直达波的目的[4]。这一新方法的原理是通过单声源延迟反相激励从源头上消除钻铤直达波。在测井中利用这种新方法，由于不再对钻铤进行周期性刻槽或变径隔声，就会增大钻铤的抗扭转力的强度，降低测井风险，并且该新方法还可以拓宽钻铤直达波隔声阻带，从而提高测量井眼周围地层横、纵波传播速度的精度。同时自适应有源噪声控制技术，还能消除井下低频高斯白噪声，提高地层波信号的信噪比。

1 研究内容

1.1 基本原理

图1中，Tf表示一个真实的发射声源，Tn表示一个虚拟的发射声源，二者在钻铤轴向的时间间隔设为τ。接收器R1和Rj(j=1,2，…,N)组成一个间隔为d的声波接收阵列。并且接收器R1距发射声源Tf长度为TR。

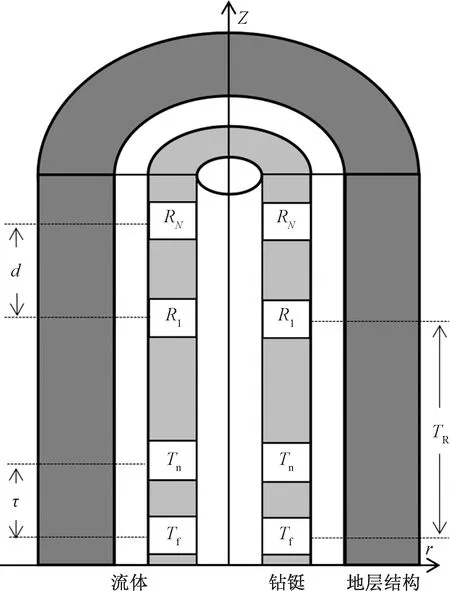
图1 单源反相激励声波测井方法示意图Fig.1 Schematic diagram of single-source reverse-excitation acoustic logging method

图2中，A1表示发射源Tf的声波振幅，A2表示发射源Tn的声波振幅，τ表示Tn滞后Tf发射的时间间隔。

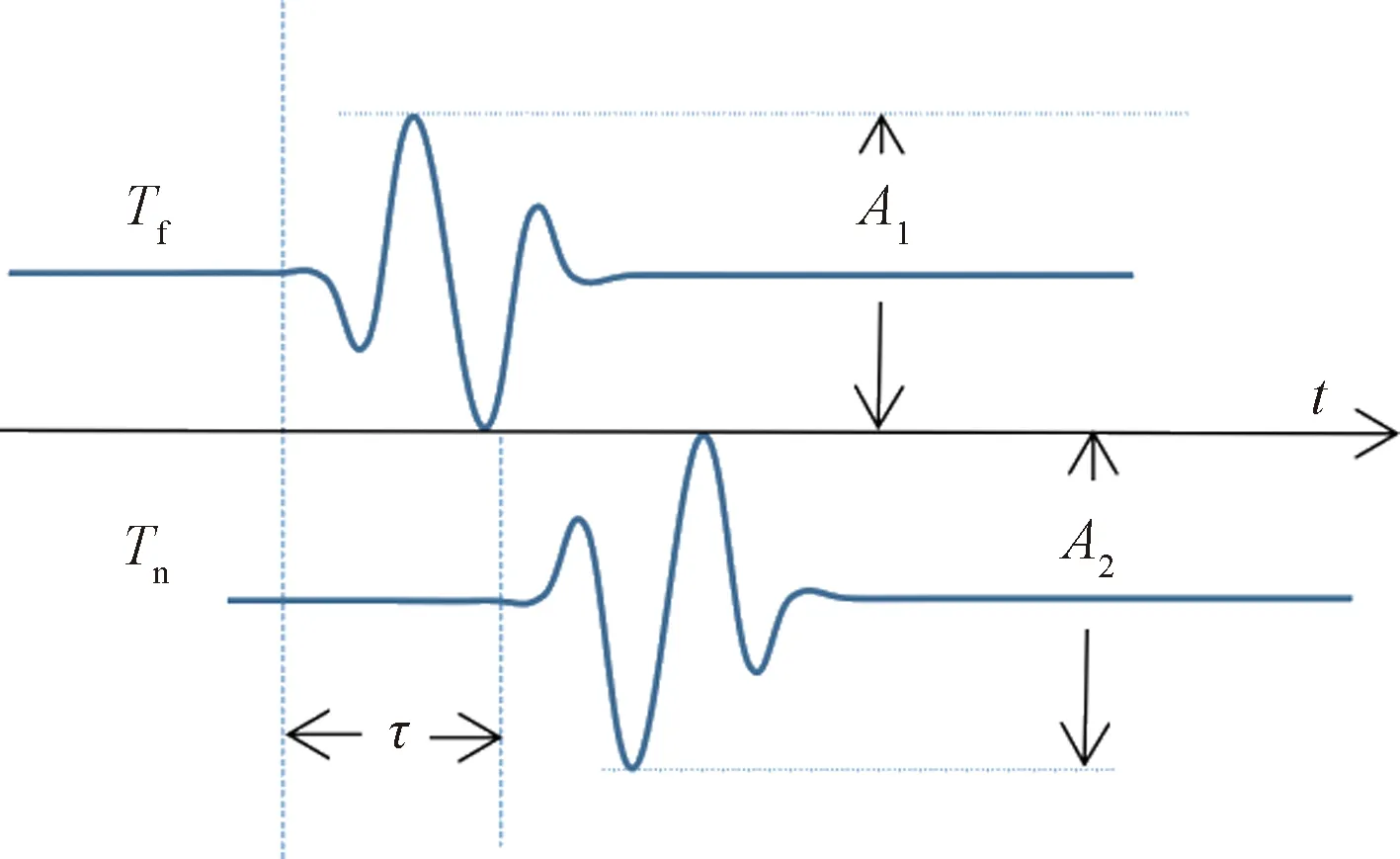
图2 单源反相激励发射时序示意图Fig.2 Sequence diagram of single-source inverse excitation emission

单声源延迟反相激励的原理如图1所示，该新方法采用一个真实的发射源Tf和一个虚拟的发射源Tn，二者在钻铤轴向的时间间隔设为τ。测井时，Tf首先受激发射测井声波，发射幅度为A1，Tn延时一段时间τ之后受激发射声波(发射时序如图2所示)，发射极性与Tf相反，发射幅度为A2。在两个发射源发射测井声波的同时，采集接收器阵列(R1,R2,…,RN)上的信号并记录。选择合适的参数A1、A2及τ，使得在任意一个接收器Rj的位置上，都有真实发射源Tf和虚拟发射源Tn通过钻铤所激发的钻铤直达波同时到达。由于这两列激发出的钻铤直达波极性相反、幅度相当，在同一接收器Rj的接收波形中，两列激发出的钻铤直达波相互叠加后干涉相消，即达到消除钻铤直达波的目的[5-6]。对于给定已知型号的钻铤，其受激发射的钻铤直达波的波速是固定和已知的。因此，在单声源延迟反相激励过程中，只要固定发射源Tf，选取合适的延迟时间τ，给接收器Rj添加一个同频反相的钻铤直达波，实现不采用隔声装置进行隔声，就能达到消除钻铤直达波的目的。同时，由于钻铤直达波被压制，地层波也就变相得到增强，增大地层波的信噪比，就可以提高测井数据的准确性。

1.2 理论推导

随钻声波测井原理可以用图1所示的径向分层模型模拟。从井轴向外依次是钻铤内流体、钻铤、钻铤外流体，最外层是无限大的弹性地层。对此模型建立柱坐标系，声源T和接收器RN均位于钻铤外环，通常随钻测井仪使用单极子圆柱体压电换能器，所以使用圆环状声源来模拟该系统[7]。假设随钻声波测井仪是圆柱状系统，那么单极子环状声源可以表述为沿半径为r的圆周上分布的一系列子点源，则声源处在波数域内的径向位移为

(1)

图1中各层介质中的位移矢量U满足矢量波动方程，其通解为

(2)

纵波位移势函数Φ、横波位移势函数Γ在频率波数域可表示为

(4)

(5)

式中：m为钻铤中纵波径向波数；n′为钻铤中横波径向波数；p为地层中纵波径向波数；s为地层中横波径向波数；vPC、vP分别为钻铤和地层中的纵波速度；vSC、vS分别为钻铤和地层中的横波速度；ACP、BCP、ACS、BCS、AO、BO、BP和BS均为待定系数。

由于各边界均为液固边界，满足径向位移连续、径向正应力连续、切向应力为零的边界条件，根据上述边界条件及圆环状声源径向位移方程建立方程组，可求解出各待定系数。由此可确定钻铤上声波的响应函数为

A(k,ω)=ρfω2[AOI0(αf)+BOK0(αf)]

(6)

式(6)中：ρf为流体密度。

对于圆环状单极子声源Tf，距离声源z处钻铤外环上的声压可以表示为

exp(ikz-itω)dkdω

(7)

式(7)中:S(ω)为声源Tf的频谱。同理，对于距声源Tf时间间隔为τ的虚拟声源Tn而言，在同一接收器上的声压为

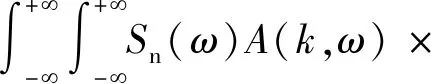
exp[ik(z-τvt)-itω]dkdω

(8)

式(8)中：Sn(ω)为声源Tn的频谱；vt为钻铤直达波速度。对虚拟声源Tn，除采用同样的频谱Sn(ω)外，还需要在时间域上对源信号延迟时间τ，这样虚拟声源Tn的声源函数可表示为

Sn(ω)=-cS(ω)exp(iτω)

(9)

(10)

式中：c为声源Tn波谱与声源Tf波谱的振幅比，将式(8)和式(9)叠加并整理得该单声源延迟反相激励时的声压为

S(ω)A(k,ω)exp(ikz-itω)dkdω

(11)

对于实际工业应用的钻铤来说，钻铤直达波速度vt通常为5 000 m/s。改变c的值，可以得到较好的钻铤直达波压制效果，而钻铤直达波幅度的衰减主要与传播距离(几何衰减)、工作频率及钻铤尺寸等参数有关[8]。在式(11)中，令c=1(c通常接近1)并与式(7)对比，发现单声源延迟反相激励和传统单源激励的区别在于其接收声压表达式中被积函数里增加了一个滤波因子，如式(12)所示：

(12)

这相当于在频率-波数域(ω-k)内嵌入了一个带阻滤波函数。即响应函数中含有速度近似等于钻铤直达波速的波的时候，这种波将被消除。因此，只要地层波和钻铤直达波的速度存在差异，钻铤直达波就能被识别并被消除。这样，通过增大声源的发射功率来增加信号强度，并针对地层波到达的时段进行数据采集，就能得到信噪比较高的地层声波信号，这为后续进行数据处理提取地层波的速度提供了较高质量的数据[9]。

1.3 理论模拟

用理论模拟的例子说明这种单声源延迟反相激励的效果。通过图1的模型计算式(6)中的响应函数A(k,ω)，再通过实轴积分方法计算式(11)，即可以得到理论接收波形。图3、图4为软地层中的例子，从下到上各接收器Rj距发射声源Tf的距离依次为3.00、3.15、3.30、3.45、3.60 m。声源中心频率取5 kHz，取vt=5×103m/s，τ=30 μs。接收阵列第一个接收器距Tf的距离TR=3 m。理论模拟的模型参数如表1所示，采用的测试声源函数为Ricker子波，得到如图3、图4所示波形。

图3 软地层理论单源5 kHz波形Fig.3 Single source 5 kHz wave form of soft formation theory

图4 软地层理论单源反相激励后的波形Fig.4 Waveforms after single source inversion excitation in soft formation theory

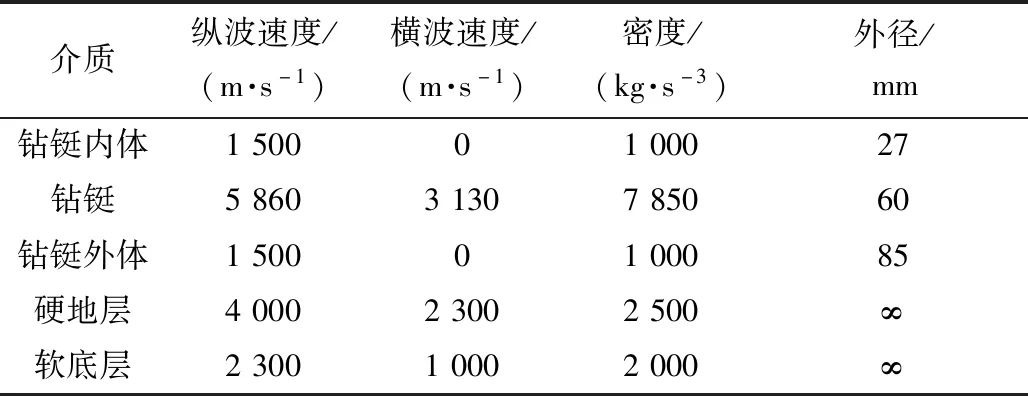
表1 随钻单极子测井的理论模拟参数Table 1 Theoretical simulation parameters of LWD monopole logging

图3是单源激励时理论计算得到的阵列波形，即式(11)中令c=0时，在2 500 μs时段内能看到两种振型的波，分别是钻铤直达波和地层纵波(波至由标识斜线给出)。图4是经过单声源延迟反相激励时理论计算得到的阵列波形，由于单声源延迟反相激励对钻铤直达波的压制作用，接收波列中观测不到钻铤直达波，只有地层纵波。这个例子直观地展示了提出的单声源延迟反相激励原理模型消除钻铤直达波的效果。

由表1可知，通常对于软地层来说，地层纵波速度与钻铤直达波差别较大，因此在时间轴上能够很好区分开来，而且地层纵波幅度较大，通常在测量中容易识别。但在实际应用中，由于软地层中地层波信号的衰减比较严重，导致地层波幅度变小，而采用单声源延迟反相激励方法消除钻铤直达波后更有利于地层纵波信号的采集，可以提高地层纵波信号的信噪比，为后续提取地层波的速度提供了较高质量的数据。

2 LMS算法

1965年，维德罗和霍夫首次提出了最小均方自适应算法(least mean square，LMS)[10]。该算法是沿着权值梯度估值的负方向进行搜索，最后达到权值最优，实现滤波器的输出信号y(n)与期望输出信号d(n)之间的误差e(n)最小[11-13]。算法核心思想是利用一次采样获得的平方误差e2(n)替代均方误差E[e2(n)]，以达到简化梯度估计的目的[14]。由于LMS 算法具有不需要输入信号和噪声的统计先验知识，通过自我学习和调整，就可以达到最优状态的特性，故非常适合应用于随钻声波测井环境中。图5为基于LMS算法的自适应有源控制系统的原理框图。

图5 基于LMS算法的系统框图Fig.5 System block diagram based on LMS algorithm

图5中，Hx(z)、Hy(z)、Ht(z)分别为各通道传递函数；F(n)为n时刻输入的初级声源信号；x(n)为参考信号；d(n)为期望输出信号；y(n)为滤波器输出次级信号；s(n)为误差接收换能器拾取的次级声场信号；e(n)为d(n)和s(n)之间的误差信号估计。且各信号间存在如下关系。

x(n)=f(n)*hx(n)

(13)

d(n)=f(n)*ht(n)

(14)

y(n)=WT(n)·x(n)

(15)

s(n)=y(n)*hy(n)

(16)

e(n)=d(n)+s(n)

(17)

式中：*表示卷积；WT(n)为W(z)的时域转置矩阵；hx(n)为Hx(z)的时域变换，hy(n)为Hy(z)的时域变换，ht(n)为Ht(z)的时域变换。

由于在最速下降法中的梯度表达式为

(18)

Un=Wopt-W(n)

(19)

式中：W(n)为n时刻N阶自适应滤波器的权系数；Un为滤波器的权值偏差；Wopt为维纳-霍夫方程的矩阵形式，通长用W表示。在LMS算法中，用一次采样获得的平方误差e2(n)替代均方误差E[e2(n)]，就可得到LMS算法的梯度表达式为

-2e(n)X(n)

(20)

用误差信号e(n)控制自适应滤波器的抽头权向量，使自适应滤波器权系数矢量收敛至稳态。由最大梯度法原理就可得到LMS算法的滤波器权系数的迭代公式为

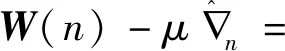
W(n)+2μe(n)X(n)

(21)

式(21)中：μ为控制算法稳定性和收敛性能的步长因子。在实际应用中，一般已知输入信号功率和滤波器阶数，可以选用合适的步长因子μ。当LMS算法收敛时，步长因子μ取值为0<μ<1/λmax，λmax为输入信号自相关矩阵的最大特征值。

在单声源延迟反相激励原理模型建立中，如式(11)所示，只有当选用c=1时，发射声源Tf和虚拟声源Tn所激发的钻铤直达波在接收端Rj处才能干涉相消，但在实际测量中，很难实现发射声源Tf和虚拟声源Tn所激发的钻铤直达波在接收端Rj处幅度和相位均匹配，但通过使用LMS算法，只要选用合适的步长因子就可以较好地解决这个问题，达到工程实践中消除钻铤直达波的目的。

3 基于LMS算法的仿真测试

3.1 测试环境搭建

随着计算机技术、自动化技术和软件技术的发展，传统的声学测量仪器仪表正在突破体积大、精度低、自动化程度低的限制。美国国家仪器公司NI(National Instruments)首次提出虚拟仪器测量的概念，在传统仪器测量领域引发了一场重大的变革[15]。LabVIEW是依托虚拟仪器技术的一种图形化编程语言，用于测控系统的开发与仪器的集成化。基于LabVIEW平台的测控系统开发，在科研与工程领域中得到了广泛的应用[16-17]。实验中，开发了一套基于LabVIEW平台开发的多功能声学参数的测控系统，打破传统声学测量中各硬件设备复杂连线的局面和复杂操作的弊端，将利用虚拟仪器开发技术的多功能声学测量仪应用到随钻声波测井中噪声控制技术的试验测量中。

由表1、图3可以看出，钻铤直达波较声波在其他介质中的传播速度快，尤其在软地层中表现明显。结合LMS算法理论原理，提取能够将接收到钻铤直达波与其他波形分开时的接收换能器R2的信号，作为LMS算法的期望信号d(n)，将R1接收到的信号作为LMS算法的x(n)输入进LMS算法滤波器后，输出的误差信号e(n)即为无钻铤直达波干扰的地层波信号。同时反馈的e(n)信号再控制LMS算法滤波器，提高算法的收敛速度，降低稳态失调。这里的期望信号d(n)实际就是单声源延迟反相激励中的虚拟声源Tn。

如图6所示，在软地层理论模型中，声源输出15 kHz声信号，经过钻铤传播后，在接收端接收到的钻铤直达波比5 kHz声源信号的钻铤直达波晚了大约150 μs，所以又对随钻测井中使用的25 kHz范围内的声波以1 kHz为步长进行实验，采样并收集数据，绘制钻铤直达波频散曲线[18]。

图6 软地层理论单源15 kHz波形图Fig.6 Single source 15 kHz wave form of soft formation theory

钻铤直达波频散曲线(图7)表明，钻铤直达波在5～25 kHz的波速随着频率的增大而减小。在15～20 kHz频段内波速随频率明显下降。对于5 kHz范围的低频激发，钻铤直达波频散效应较小、速度较快，钻铤直达波和P波在时域中有较大的时间间隔T。而对于15 kHz左右的频率范围，频散效应已相当明显，钻铤直达波速度较慢，钻铤直达波和P波在时域中有较小的时间间隔T，不易区分。在实际测量中要考虑钻铤直达波频散效应，对于不同频率的测试波调整接收换能器R2的不同接收距离L，才能保证采样到完整且独立的钻铤直达波。通过同步时钟模块后，作为LMS算法的期望信号输入到算法模块中，经过LMS算法滤波后，在示波器上可以观察采用该方法后的消除效果。

图7 钻铤直达波频散曲线Fig.7 Drill collar direct wave dispersion curve

3.2 仿真实验

为了验证上述方法及其工作原理，使用的钻铤内外直径分别为30、120 mm，并在实验室进行了初步的实验，图8为实验原理框图。图8中的发射换能器、接收换能器R1和接收换能器R2，均为圆环状压电陶瓷换能器，并固定在钻铤上，发射换能器和接收换能器R1之间的距离TR=3 m。为了提高声耦合，发射换能器和接收换能器均与钻铤之间涂抹凡士林。

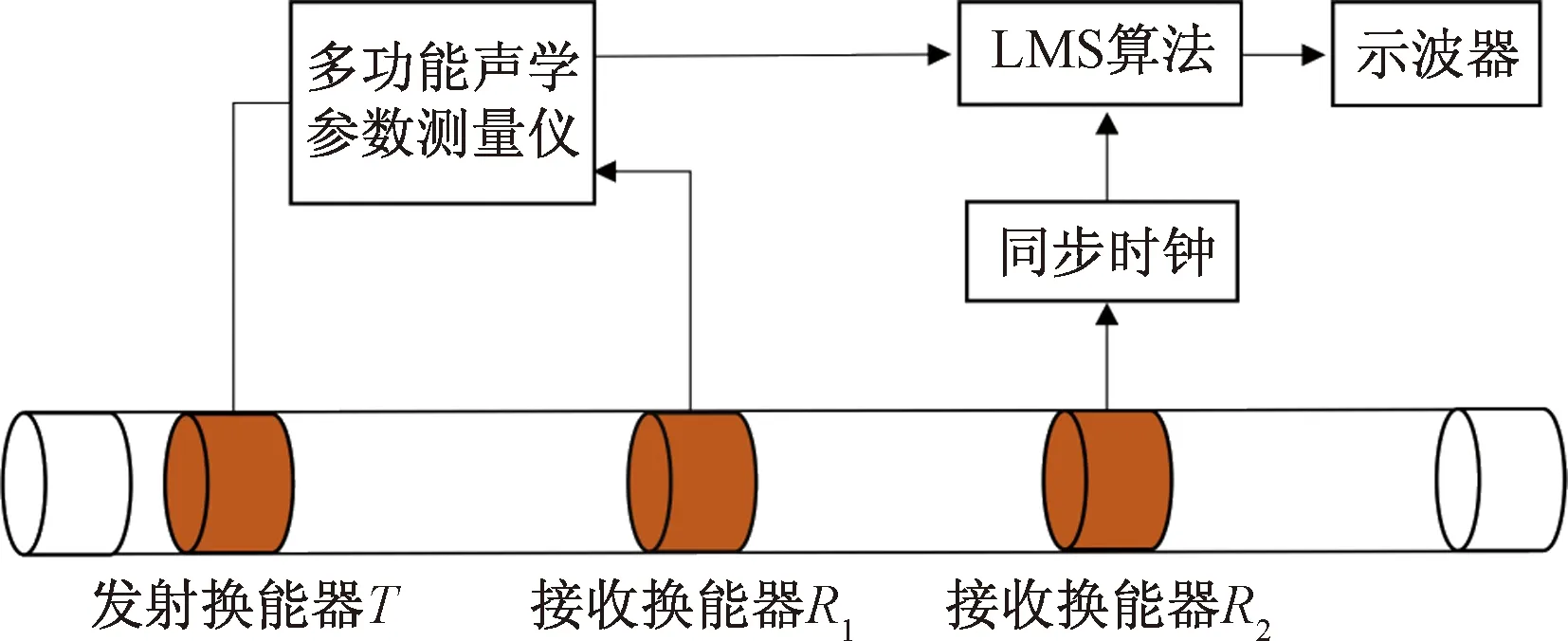
图8 基于LMS算法的控制测试框图Fig.8 Control test diagram based on LMS algorithm

利用基于LabVIEW平台开发的多功能声学测量仪产生测井声信号激励，其发射电路能产生高压脉冲激励发射换能器。发射换能器的发射延迟时间及幅度连续可调，最大幅度可达2 000 V，幅度连续可调，声源的频率可调，图9为多功能声学测量仪界面图[19]。

图9 多功能声学测量仪界面图Fig.9 Interface diagram of multifunctional acoustic measuring instrument

考虑到钻铤直达波的频散效应对实际测量的影响，测试声信号的发射频率为5、10、16、18、20 kHz。

实验时将钻铤置于空气中，调整接收换能器R2的位置，用数字示波器记录不同频率的接收延迟为后续软件测试提供数据。

3.3 实验结果

图10为试验中接收换能器R1接收到的测试声波和钻铤直达波的合成波形；图11为试验中接收换能器R2接收到的测试声波的波形。将接收换能器R2和接收换能器R1接收到的两列声波，通过信号同步处理后，送入LMS算法模块处理，得到如图10所示的滤波结果。

图10 接收换能器R1接收波形Fig.10 Receiving waveform of receiving transducer R1

图11 接收换能器R2接收波形Fig.11 Receiving waveform of receiving transducer R2

由图12可以清楚地看出，叠加钻铤直达波的合成波信号，经过LMS算法滤波后，测试地层波的波形能够被较为清晰地还原出来，说明将这种改进的LMS算法应用于随钻声波测井中钻铤直达波的消除领域是有效果的。

图12 LMS算法模块滤波结果Fig.12 LMS algorithm module filtering results

4 结论

在实际测量中，如波的衰减、频散以及发射换能器及其工作载荷的差异等，难以将钻铤直达波完全抵消。尽管如此，实验测量中的钻铤直达波可以得到有效压制，这在实际的随钻测量中是至关重要的。此外，由于实验中发射换能器距离仪器端面较近，反射波很强，由于过快的反射波会干扰正常的消声处理，导致接收到的后续钻铤直达波有很长的持续时间，所以时间截止在2 500 μs但是，在钻铤直达波为主的时段内，钻铤直达波的压制效果还是十分明显的，验证该方法是有效的。得到以下结论。

(1)根据声波在钻铤、流体介质、硬地层和软地层中的传播速度不同，创新性地提出了一种“单声源延迟反相激励”的新技术，根据测试结果可以看出，该技术能够消除钻铤直达波，从而达到不再对钻铤进行刻槽隔声，增大了钻铤的抗扭转力的强度，降低测井风险的目的。

(2)LMS算法不仅可以应用在压制钻铤直达波方面，而且该算法还可以应用于消除钻井下的低频噪声，尤其是对5～25 kHz的低频噪声的压制能力强，可以变相提高了测井声波的信噪比。

(3)在实验中把声学测量过程等效为一个并联传输网络系统，在理论上考虑电驱动信号对辐射声信号特性的影响，应用开发的声学测量仪对随钻声波声波测井中钻铤直达波的控制进行实验。