基于不等式约束的重力三维聚焦反演

刘 星，邓居智，陈 晓

(1.东华理工大学核资源与环境国家重点实验室，南昌 330013;2.东华理工大学地球物理与测控技术学院，南昌 330013)

三维物性反演是重力反演研究的重点，通过数据利用反演方法推算出地下的物性分布情况，从而达到确定地下地质地球物理模型的目的。近年来，在Tikhonov正则化理论框架下，中外学者针对三维反演方法开展了大量研究工作，新的反演方法的研究一直是重力反演研究的热门。早期反演得到的结果多是光滑约束的，为了得到更加突出尖锐边界的结果，出现了聚焦算法。Last等[1]最早提出最小支撑泛函来进行重力反演的思想，为后来的聚焦反演奠定了基础；Portniaguine等[2]通过引入最小梯度支撑泛函来实现聚焦反演，得到清晰且更聚焦的结果；Zhdanov等[3]在重力梯度数据反演中采用三维聚焦反演方法并取得了与理论模型边界较吻合的反演成果；Rezaie等[4]利用聚焦反演方法实现了三维重力数据的反演，得到一个能较好吻合真实异常体形状和范围的聚焦解。中国方面，刘小军等[5]将聚焦反演方法应用于二维大地电磁反演中获得了比传统方法更聚焦的反演结果；粟学磊等[6]将聚焦反演方法应用于重力资料反演中，并引入深度加权函数和异常源外扩方法来进一步改善反演结果；陈闫等[7]将三维聚焦反演方法应用于重力梯度数据中，得到一个聚焦解，并成功地框定了异常体的分布范围；杨娇娇等[8]实现了三维重力梯度数据的聚焦反演，并与最平滑稳定泛函反演结果进行了对比，结果表明该方法能获得更聚焦的结果；刘希康等[9]引入粗糙度约束和深度加权，对重力数据进行了三维聚焦反演，较清晰地还原了异常体的边界；高秀鹤等[10]对三维重力梯度数据聚焦反演方法进行了研究，反演结果显示异常体密度分布集中且边界清晰。

由于三维反演方法会出现负的或者很大的异常值的现象，超出了实际真实异常值范围，使得反演结果出现多解性问题。因此，为了解决这个问题，引入不等式约束让反演参数限制在有意义的约束范围内。如何根据先验物性信息，选择有效的约束函数来将上下限约束融入反演中，是反演领域的研究热点。目前，各种方法已经应用于不同的反演方案中以实现物性不等式约束。绝对约束法[2,11-12]是比较常见的解决方法，该方法是将迭代过程中所有超出取值范围的反演参数赋值为其接近的上限或下限值，从而使反演得的物性参数值保持在上下限范围内。Li等[13]引入了对数惩罚函数法(障碍函数法)将物性约束添加到目标函数中进行反演，该方法是沿模型可行域的边界形成了一个对数屏障以防模型参数在最小化过程中越界，从而实现上下限约束；在Li等[13]的基础上，Zhang等[14]通过在模型增广目标函数中使用拉格朗日乘数的方法对三维位场数据的反演中不等式约束，将反演参数搜索区间限定在有效的取值区间内，从而改善反演解的多解性问题；王智等[15]用惩罚函数法修改目标函数，利用权重因子将物性约束引入到非线性共轭梯度反演目标函数中，但需要人为确定对应的权重因子取值；Kim等[16]在最小二乘反演中引入了不等式约束，并利用对数变换函数方法将变化的物性参数值约束在有效的范围内；Commer[17]在三维重力反演中引入反双曲线正切变换方法，在上下限范围内约束物性参数在无界域中的转换，从而保证反演参数的合理性；刘斌等[18]通过对数变换方法来进行基于不等式约束的反演，将参数转换为无界域的新参数，利用新的参数来完成反演迭代过程，最终反演的参数值比未施加不等式约束前更接近真实异常值，有效减少了一些假异常；刘银萍等[19]将上下限约束以对数变换函数形式引入到重力三维反演中，将不具有实际物理意义的反演结果转化到合理的范围，有效地限制了反演结果中剩余密度分布的数值范围，还原模型剩余密度；Lin等[20]通过在三维反演中利用对数变换函数在有效范围内约束密度变化，控制反演解的范围，从而降低了反演多解性问题；Rezaie等[21]对具有稀疏约束的数据空间反演算法进行了修改，使得物性边界约束可以以对数变换函数的形式应用于三维重力反演中，虚假构造得到减少，反演异常值接近真实值，异常体更加突出。

可以看出，聚焦反演和不等式约束均是反演领域的研究热点和前沿。基于此，尝试将不等式约束引入三维重力聚焦反演，并通过模型试验来验证方法的有效性。

1 基于不等式约束的重力三维聚焦反演

1.1 聚焦反演

三维重力聚焦正则化反演目标函数的表达式可写为

Pα(m)=φ(m)+αS(m)={Wd[A(m)-d]}T{Wd[A(m)-d]}+

α[WeWm(m-mapr)]T[WeWm(m-mapr)]

(1)

式(1)中：Pα(m)表示反演目标泛函；φ(m)表示数据拟合函数；S(m)表示模型稳定函数；α为正则化因子；A(m)为正演响应函数；m为模型参数；d为观测数据；mapr为模型先验信息；Wd、Wm分别为数据和模型加权矩阵；We为聚焦加权泛函矩阵。采用文献[22]提出的自适应正则化算法确定正则化因子。为了避免得到传统反演方法过于光滑的反演结果，采用的模型稳定泛函为最小支撑泛函[22]，其对应的聚焦加权泛函矩阵为

(2)

1.2 对数不等式约束

为了将反演的参数控制在合理的物性约束范围内，可以将模型物性参数取值范围作为不等式约束条件应用到反演过程中，即

ρmini≤mi≤ρmaxi，i=1,2,…,m

(3)

式(3)中：mi为第i个网格单元的物性参数；ρmini和ρmaxi分别为此网格单元的物性下限和上限。

(4)

(5)

(6)

(7)

因此，新的模型参数的灵敏度矩阵表示为

(8)

1.3 共轭梯度法

共轭梯度(conjugate gradient，CG)算法解决目标函数最小化的问题，CG算法的计算流程为

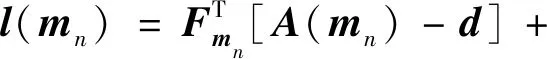
(9)

βn=‖ln‖2/‖ln-1‖2

(10)

(11)

(12)

(13)

(14)

2 模型试验

为了验证基于不等式约束的聚焦反演的有效性，以重力反演为例，设计了两个密度模型，采用规则六面体单元剖分网格，通过利用文献[24]中的直立长方体重力异常积分解公式进行正演计算，再对模型进行三维反演。观测区剖分为21×21 个观测点，将地下均匀半空间剖分为21×21×10 个网格，网格间距均为50 m，x方向为正东方向，y方向为正北方向。

2.1 单块体模型

单块体模型分布如图1所示，在密度设置为0的地下均匀半空间中，存在一个中心坐标为(475、450、200 m)的长方体异常体，正东向边长为350 m，正北向边长为300 m，异常体顶部埋深为100 m，底部埋深为300 m，其剩余密度为0.5 g/cm3。

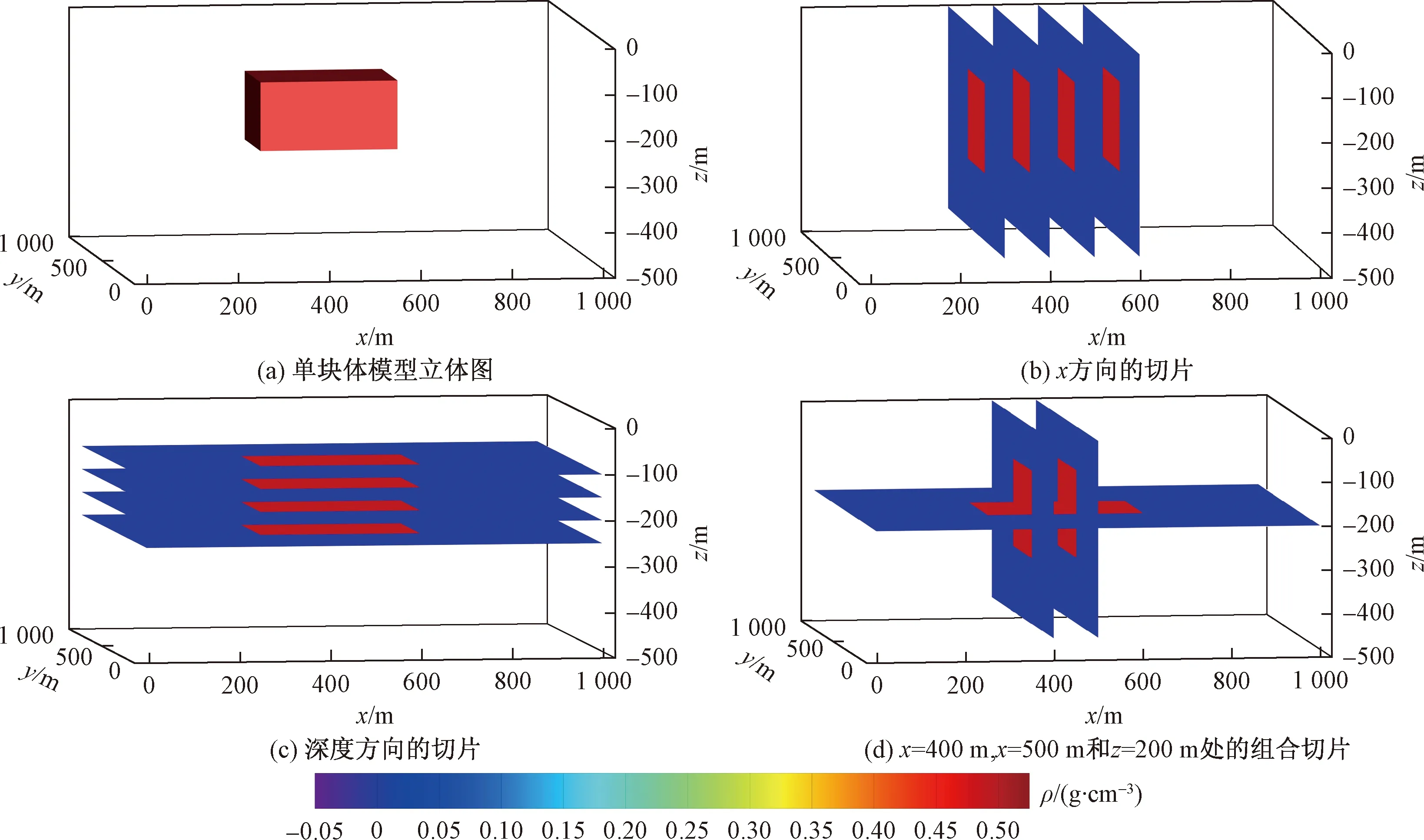
图1 单块体模型切片和立体图Fig.1 Single cube model slices and 3D structure diagram

设计了如下的对比试验：方案一是无正则化项反演；方案二是聚焦反演；方案三是基于不等式约束的聚焦反演，该方案给所有的模型均匀半空间网格单元体赋予密度约束范围为0～0.6 g/cm3；方案四是基于分区域不等式约束的聚焦反演，在深度范围100 m≤z≤300 m的区域将不等式约束范围设为0～0.6 g/m3，而其余区域网格设置为0～0.2 g/cm3。为了能更好地进行对比，4种反演方案的反演参数均是一致的，其中模型先验信息mapr=0，反演初始模型选取为0，反演迭代收敛终止条件为均方误差(root mean square，RMS)=0.01。

图2～图5分别为无正则化项反演、未施加不等式约束聚焦反演、不等式约束条件下的聚焦反演和分区域不等式约束聚焦反演结果。对比3种反演方案的反演结果可看出，无正则化项反演所得的密度分布立体图与理论模型偏差较大[图2(a)]，反演密度集中分布于地表附近0～100 m处，图2(b)～图2(d)显示异常值最大值为0.3 g/cm3，相对原模型较小，无法还原出原模型的位置分布及密度。未施加不等式约束的聚焦反演结果如图3所示，图3 (a)中显示异常体与理论模型在位置上相近，但异常体的分布范围比理论模型大，图3(b)所示的正东方向切片图表明在100～300 m深处较好地吻合理论模型，在深度300～500 m处，反演结果存在0.2～0.5 g/cm3的假异常。图3(c)表明反演的模型分布范围在浅层100～200 m基本与原模型吻合，水平分辨率也相对较高，聚焦效果明显，深部边界拟合相对较差。从图3(b)～图3(d)可以看出，反演结果出现了一些负密度，且异常体中心部位出现大于真实异常值的密度，异常体剩余密度为0.3～0.53 g/cm3。

图2 无正则化项反演结果切片和立体结构Fig.2 The slices and 3D structure of the inversion results without regularization

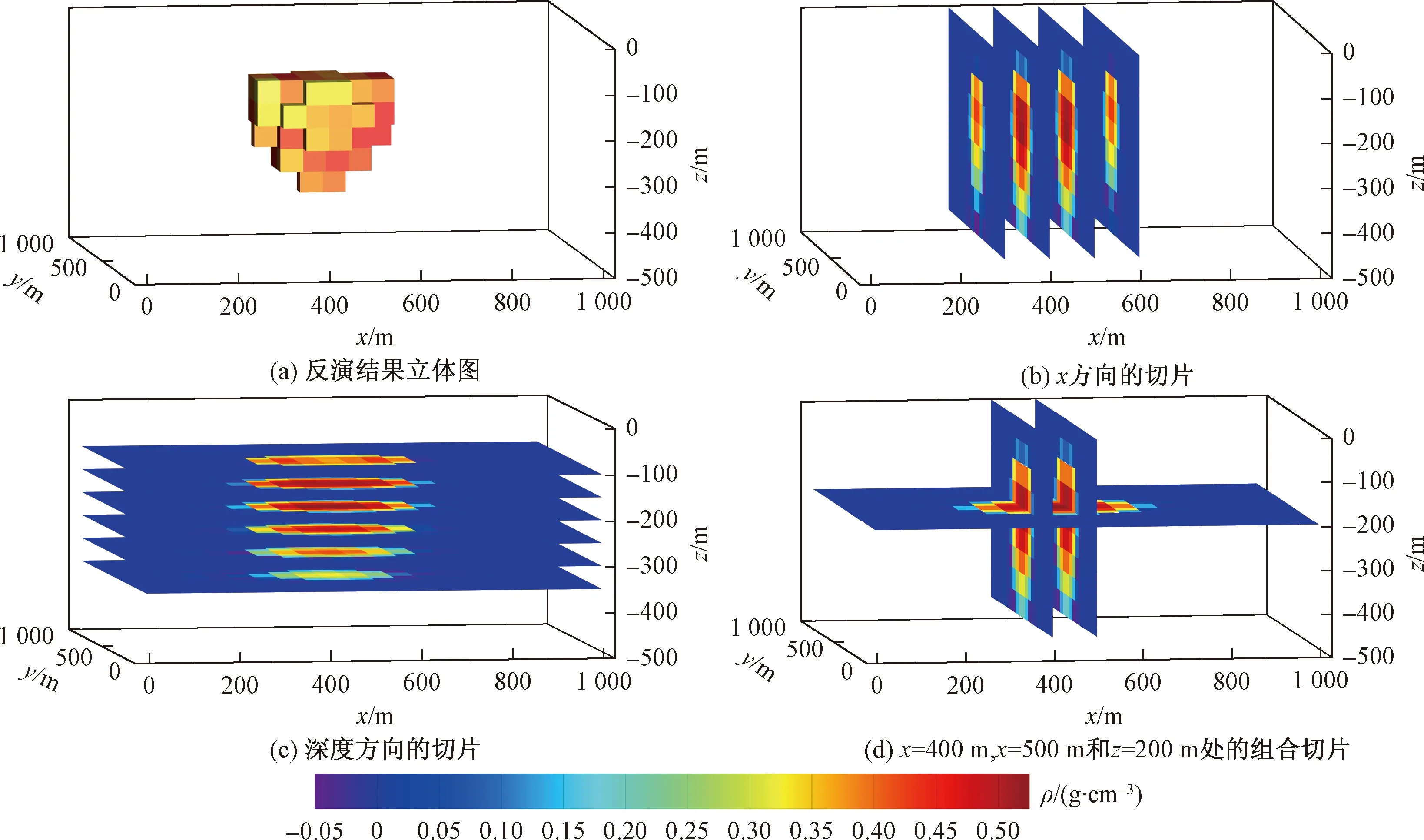
图3 未施加不等式约束的聚焦反演结果切片和立体结构Fig.3 The slices and 3D structure of thefocusing inversion results without inequality constraints

图4 不等式约束条件下的聚焦反演结果切片和立体结构Fig.4 The slices and 3D structure of thefocusing inversion results with inequality constraints

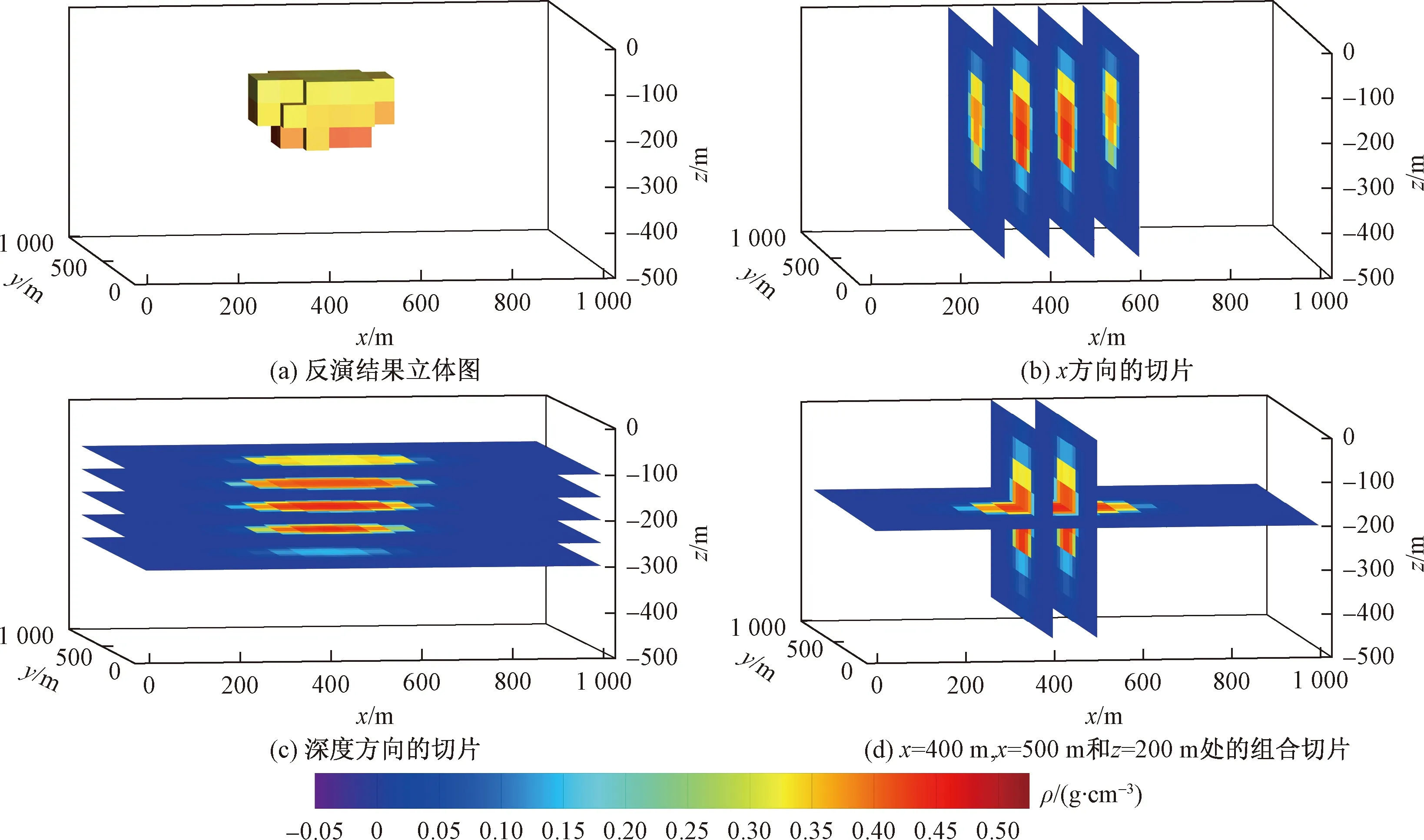
图5 分区域不等式约束条件下的聚焦反演结果切片和立体图Fig.5 The slices and 3D structure of thefocusing inversion results with subregional inequality constraints

相较未施加不等式约束的反演结果而言，图4的施加不等式约束聚焦反演的密度模型与理论模型位置、分布形状基本一致[图4(a)]，能够较好地还原原模型分布形态，并且由图4(b)～图4(d)的切片图像可以看出，没有出现密度范围之外的值，异常值不超过0.5 g/cm3，假异常得到了很大的减少，深度方向的分辨率得到了提高，验证了不等式约束能够减少解的多解性问题，提高聚焦反演解的质量。虽然还是存在异常体的底部边界较模糊的现象，在深度300～350 m处仍然存在0.3～0.35 g/cm3的虚假构造，但总体而言，基于不等式约束聚焦反演方法是可行的。

由图5可以看出，与不等式约束聚焦反演结果相比有进一步的改善，图5(a)的反演的密度模型与原模型位置、规模范围、分布形状基本吻合，图5(b)～图5(d)的切片图显示异常体剩余密度值范围为0.3～0.5 g/cm3，地下异常体深部边界信息清晰，进一步验证了分区域不等式约束可以提高聚焦反演结果精度从而还原真实异常体。图6为4种反演方案的RMS迭代误差拟合曲线，从中可看出，RMS在反演迭代初期迅速减小，随着迭代次数的增加而缓慢减小，直到达到设定的拟合值迭代结束。

图6 迭代误差曲线Fig.6 Curves of RMS Iterative error

2.2 台阶状密度模型

设有一个台阶状地下异常体，其模型分布如图7所示，是5个250 m×300 m×50 m的长方体叠加交错50 m拼接成的阶梯状模型，埋深范围为50～300 m，异常体剩余密度为Δρ=1.0 g/cm3，围岩密度均为0。

图7 台阶状模型切片和立体图Fig.7 Inclined plate model slices and 3D structure diagram

与模型一类似，设计了如下的对比试验：方案一是无正则化项反演；方案二是聚焦反演；方案三是基于不等式约束的聚焦反演，该方案给所有的模型均匀半空间网格单元体赋予密度约束范围为0～1.1 g/cm3；方案四是基于分区域不等式约束的聚焦反演，在深度范围50 m≤z≤300 m的区域将不等式约束范围设为0～1.1 g/cm3，而其余区域网格设置为0～0.5 g/cm3。为了更好地进行对比，4种反演方案的反演参数均是一致的，其中模型先验信息mapr=0，反演初始模型选取为0，反演迭代收敛终止条件为RMS=0.01。

图8～图11分别为无正则化项反演、未施加不等式约束聚焦反演、不等式约束条件下聚焦反演和分区域不等式约束条件下聚焦反演的结果。对比四种反演方案的反演结果可看出，图8(a)所示的无正则化项反演得到三维模型的密度集中分布于台阶状模型垂直上方的地表附近150 m内，无法还原出真实模型的真实形态，且图9(b)～图9(d)的切片图显示反演所得剩余密度异常范围小，除台阶状模型顶层阶梯对应的横向分布范围的近地表0～50 m深处出现0.9 g/cm3左右的异常值，其余范围内的剩余密度值均小于0.6 g/cm3。未施加不等式约束的聚焦反演由图9(a)表明在异常体位置出现形状与真实模型相差较大的异常体，在浅部50～100 m深度处能够较好地反映异常体的阶梯形状和边界，深部反映效果差，图9(b)～图9(d)的切片图显示在浅部50～100 m深度处能够较准确地反演出异常体形状和边界，水平分辨率也相对较高，但在深部分辨率很差，在理论模型边界外部出现了较多的假密度分布，异常体底部边界延伸到400 m，且反演的背景场密度有出现较大的负的数值-0.3 g/cm3，异常体剩余密度值在0.5～1.1 g/cm3。

图8 无正则化项反演结果切片和立体图Fig.8 The slices and 3D structure of the inversion results without regularization

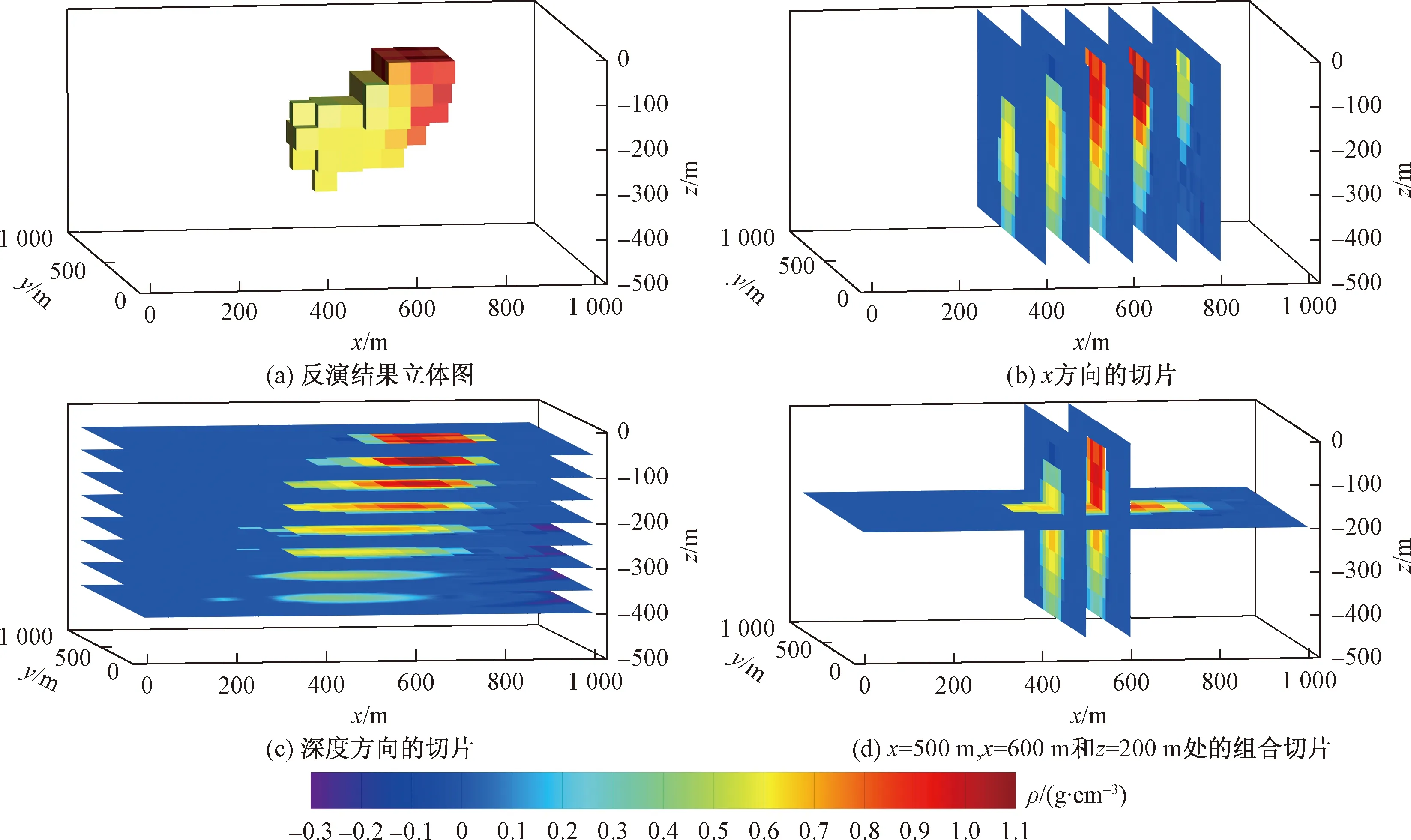
图9 未施加不等式约束的聚焦反演结果切片和立体结构Fig.9 The slices and 3D structure of thefocusing inversion results without inequality constraints

相较未施加不等式约束的聚焦反演结果而言，图10(a)为施加不等式约束聚焦反演的三维密度模型，该模型与图9 (a)对比，能较好地拟合于理论模型位置、分布范围和阶梯形状，图10(b)～图10(d)所示的切片图显示，该方法的反演异常体剩余密度范围为0.5～1.0 g/cm3，有效抑制了密度范围之外的值，水平和深度方向分辨率也得到很大改善，减少了虚假异常，也证明了基于不等式约束聚焦反演的可行性。

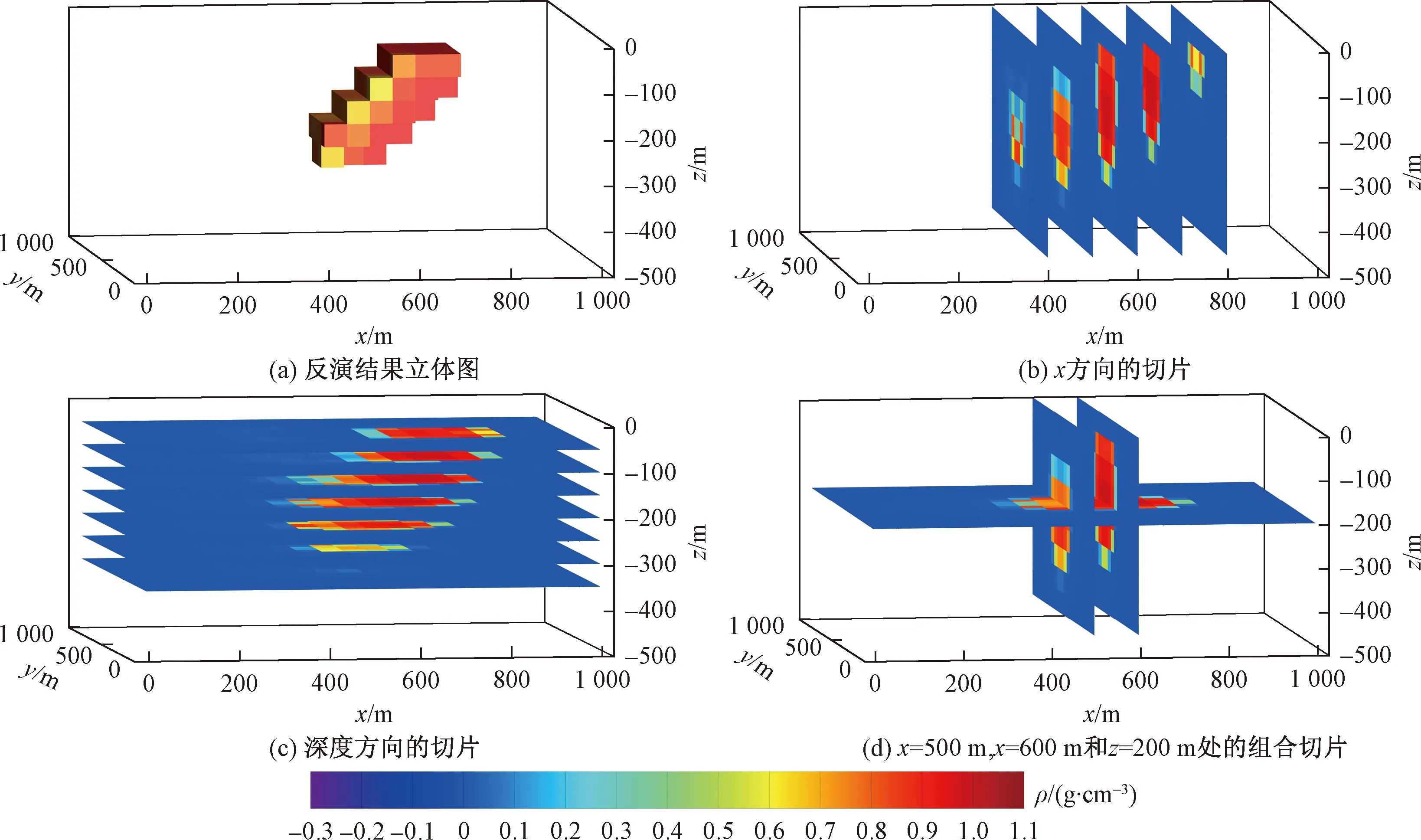
图10 不等式约束条件下的聚焦反演结果切片和立体结构Fig.10 The slices and 3D structure of thefocusing inversion results with inequality constraints

图11所示的分区域不等式约束条件下的聚焦反演结果与图10相比有进一步的改善，图11(a)显示的三维密度模型与理论模型位置、规模范围、分布形状基本吻合，与图10(a)相比，深度方向300～350 m处的缺陷得到补充，图11(b)～图11(d)的切片图显示异常体剩余密度值范围为0.5～1.0 g/cm3，异常体深部边界信息更加清晰，较好地还原了模型的真实分布特征,进一步验证了分区域不等式约束可以提高聚焦反演结果精度从而提高异常体还原度。图12为4种反演方案的RMS迭代误差拟合曲线，从图2可以看出，4种反演方案都能稳定收敛。

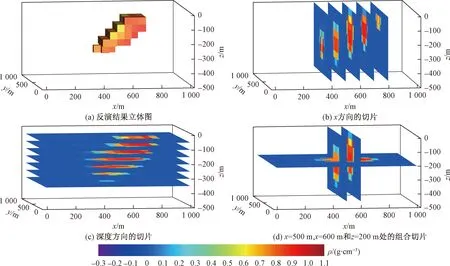
图11 分区域不等式约束条件下的聚焦反演结果切片和立体图Fig.11 The slices and 3D structure of thefocusing inversion results with subregional inequality constraints

图12 迭代误差曲线Fig.12 Curves of RMS iterative error

3 结论

将先验物性信息的上限和下限作为约束条件，以对数转换函数形式的将不等式约束融入到三维重力聚焦反演，模型试验表明以下结论。

(1)聚焦反演在浅部能够较准确地框定异常体形状和范围，但在深部存在一些虚假异常。

(2)基于不等式约束的三维聚焦反演可以将解控制在合理的物性范围之内，减少虚假异常构造的产生，此外，分区域不等式约束的加入可以提高先验物性信息应用的灵活性，反演结果更加逼近真实模型。

需要指出的，理论模型反演中给定的不等式约束的范围是较为理想的，但是在实际情况中异常体分布信息更为复杂，在将一些丰富的地质信息转化成合理的约束条件的问题上还存在困难，因此如何获得比较合理准确的边界范围以及物性的上下限约束条件需要进一步进行研究。