基于三剪能量屈服准则的应变软化岩石统计损伤本构模型研究

鄢俊彪，邹宗兴，王 飞，张 琦，罗 涛

(中国地质大学(武汉)教育部长江三峡库区地质灾害研究中心，湖北 武汉 430074)

岩石的力学性质与矿山、道路桥梁和水利水电等岩石工程的建设与安全运营密切相关。研究岩石的本构模型，定量地把握其应力-应变关系，对于探究岩石的变形破坏过程，为实际工程建设与安全运营提供理论依据，具有重要的意义。

目前，一些学者通过引入统计损伤理论，假定岩石的微元强度服从某种概率分布，从而建立起岩石的统计损伤本构模型。其中，岩石微元强度的合理度量成为一个关键问题，其反映的是岩石材料的破坏程度。曹文贵等[1-2]、张勃成等[3]、Zhao 等[4]和Chen等[5]以Drucker-Prager准则来描述岩石的微元强度，建立了岩石的统计损伤本构模型；陈松等[6]和Li等[7]基于Mohr-Coulomb准则来度量岩土材料的微元强度，分别建立了断续节理岩体和应变软化岩石的损伤本构模型；Deng等[8]分别采用Drucker-Prager准则和Mohr-Coulomb准则来描述岩石微元强度分布，并对两种屈服准则得出的岩石损伤本构模型进行了对比分析；Shen等[9]基于统一强度理论来建立应变软化岩石的损伤本构模型；汪杰等[10]、Huang等[11]、Qu等[12]和马高强[13]采用应变表征的岩石微元强度来建立岩石损伤演化本构模型。显然，这些研究仅仅是从应力或应变水平角度来反映岩石材料的屈服和损伤，而从能量角度建立岩石的损伤本构模型的研究较少，然而岩石或岩体的变形破坏实质上是能量转换的结果[14]。谢和平等[14-17]从能量的角度研究了岩石的变形破坏过程，认为能量耗散、能量释放与岩石的损伤和整体破坏密切相关，并建立了相应的岩石强度与破坏准则；彭瑞东等[18-19]在岩石变形破坏过程中能量耗散分析的基础上，建立了相应的岩石损伤演化方程；葛云峰等[20]利用室内实验和数值模拟的方法，从弹性应变能演化机制方面研究了岩体结构面的剪切破坏过程；高红等[21]和周辉等[22]从能量的角度分析岩土内摩擦材料的屈服特性，并建立了适用于岩土内摩擦材料的能量屈服准则，该准则在描述岩土材料变形屈服特性中取得了较好的效果。因此，相比于以往基于应力或应变水平构建的岩石微元强度和本构模型，从能量的角度建立起岩石的损伤本构模型更加符合岩土内摩擦材料的变形破坏特性，且物理意义将更为明确。

本文首先从岩石的微元强度服从概率分布出发，引入统计损伤理论，基于三剪能量屈服准则来度量岩石的微元强度，并建立起反映应变软化岩石的统计损伤本构模型；然后以一组岩石三轴试验数据为例，验证所建立模型的可靠性；最后深入讨论该模型中参数的物理力学意义，并测试模型的实用性。

1 岩石的统计损伤本构模型

1.1 岩石的统计损伤本构模型的建立

岩石材料在变形过程中由损伤部分和未损伤部分组成，根据Lemaitre应变等效假设[23]，岩石的损伤模型如下：

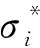
(1)

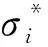
(2)

式中:E为岩石的弹性模量(MPa)；μ为岩石的泊松比；εi为岩石的应变。

将公式(2)代入公式(1)，可得到以岩石名义应力表示的岩石损伤模型：

σi=Eεi(1-D)+μ(σj+σk) (i,j,k=1,2,3)

(3)

岩石的损伤变量D为岩石中损伤部分与岩石总体部分之比。根据统计损伤理论，将宏观岩石视为由大量微单元组成，岩石变形破坏过程中这些微单元由未损伤状态向损伤状态转化，且这种损伤转化不可逆，故可将岩石的损伤变量D定义为岩石中损伤的微单元数目与总的微单元数目的比值[1]，即：

(4)

式中:ND为岩石中损伤的微单元数目；N为岩石中总的微单元数目。

假定岩石的微元强度F服从概率分布，其中Weibull分布已经被广泛地运用于岩石的统计损伤本构模型的研究中，并取得了很好的效果[1-13,24-25]。本文研究中也采用Weibull分布作为岩石微元强度的分布函数，Weibull分布的概率密度函数[26]为

(5)

式中:m、F0为Weibull分布函数的参数。

由于岩石微元强度反映的是岩石的破坏程度，当外荷载加载至F状态时岩石中损伤的微单元数目(ND)可表示为

(6)

将公式(6)代入公式(4)，可得到岩石的损伤变量为

(7)

将公式(7)代入公式(3)，并令公式(3)中i为1，可得：

(8)

公式(8)即为本文建立的岩石统计损伤本构模型。由此可知，合理地确定该本构模型中岩石的微元强度为建立模型的关键问题。

1.2 三剪能量屈服准则

相比于应力和应变，从能量的角度来分析岩石的损伤和屈服具有更加明确的意义[14-19]，同时不同于金属材料，岩土材料具有独特的内摩擦性质，鉴于此，本文采用三剪能量屈服准则作为岩石微元强度的度量。

图1 三剪能量屈服准则示意图Fig.1 Diagram of triple shear energy yield criterion

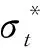
(9)

式中:G为岩土材料的剪切模量(MPa)；K为一常数;φ12、φ23和φ13分别为岩土材料的3个最大内摩擦角(°)(见图1)。

(10)

公式(9)和(10)中均是以岩石的有效应力形式表示的岩石微元强度，故将公式(1)分别代入公式(9)和公式(10)，化为以岩石名义应力形式表示的岩石微元强度，则有：

(11)

(12)

根据公式(3)，可得：

(13)

将公式(12)和(13)代入公式(11)，即可得到基于三剪能量屈服准则表征的岩石微元强度，将该岩石微元强度表达式代入公式(8)，即可得到本文提出的基于三剪能量屈服准则的应变软化岩石统计损伤本构模型。

1.3 模型参数确定

本文提出的岩石统计损伤本构模型公式(8)中有岩石的弹性模量E、泊松比μ、剪切模量G、内摩擦角φ13、Weibull分布函数的参数m和F0共6个参数。其中，前4个参数为岩石力学中常用的岩石变形和强度参数，通过试验即可获取；对于参数m和F0，本文采用线性拟合的方法来确定。由公式(8)分离出指数项，可得：

(14)

将公式(14)两边同时取两次对数,可得：

(15)

令:

(16)

公式(15)则简化为

y=mx+b

(17)

于是，利用公式(16)将岩石三轴试验数据简化为公式(17)的形式，然后进行线性拟合，得到的拟合直线的斜率即为参数m，再将参数m代回公式(16)中即可计算参数F0：

F0=exp(-b/m)

(18)

2 实例验证

为了验证本文提出的岩石统计损伤本构模型的可靠性，引用文献[28]中的一组经典的岩石三轴压缩试验数据。该岩石岩性为石英岩，属于硬质岩，岩样在围压σ3分别为0 MPa、3.45 MPa、6.90 MPa、13.80 MPa和27.60 MPa条件下进行常规的三轴压缩试验。该岩石的弹性模量E为9×104MPa，泊松比μ为0.15，剪切模量G为3.9×104MPa，内摩擦角φ13为31.304°。常规三轴压缩试验下有σ2=σ3，于是公式(11)可简化为

(19)

将公式(13)代入公式(19)中，并化简可得：

(20)

首先，采用第1.3节中的方法对Weibull分布函数的参数m和F0进行线性拟合求解，其中在围压σ3为0 MPa和27.60 MPa的条件下，由试验结果拟合出近似两段直线(斜率一正一负)，参考其他3个围压条件下的试验结果，取直线斜率(即m值)为正的一段。相应地各围压条件下Weibull分布函数的参数m、F0计算结果，见表1。

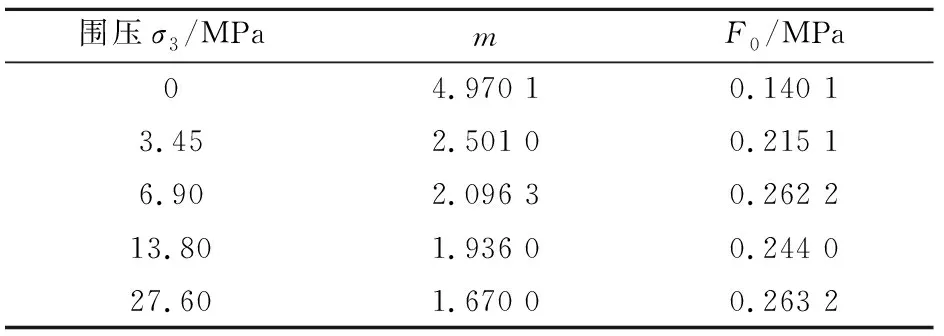
表1 各围压条件下Weibull分布函数的参数计算结果Table 1 Parameter calculation results of Weibulldistribution function under various confiningpressures

然后，将公式(20)和表1中参数代入公式(8)中，即可得到相应的基于能量屈服准则的岩石损伤本构方程。

最后，将利用该方程得到的岩石应力-应变理论曲线与相应的试验数据进行了对比，见图2。

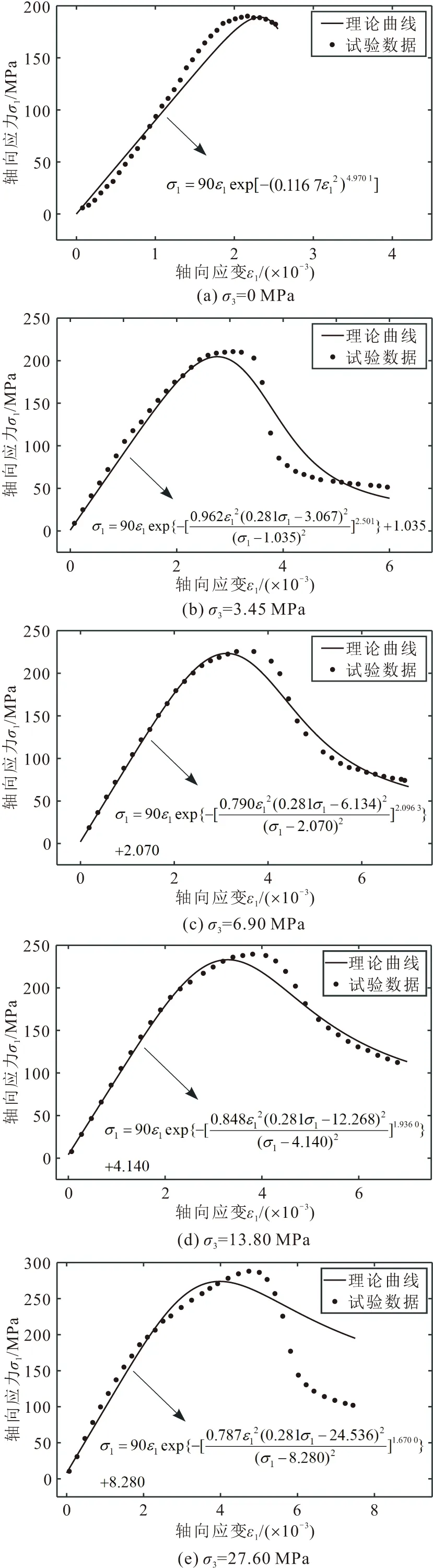
图2 利用本文模型得到的岩石应力-应变理论曲线 与试验数据的对比Fig.2 Comparison between rock stress-strain theoretical curves obtained by the model of this paper and test data

由图2可见，利用本文提出的基于能量屈服准则的岩石损伤本构方程得到的岩石应力-应变理论曲线与试验数据总体吻合度较好。对于岩石的应力-应变曲线峰前弹性变形阶段，本文模型曲线能够很好地反映曲线峰前弹性变形阶段；对于峰值强度，本文模型曲线与试验数据存在一定的误差，出现该现象的原因是参数求解采用的是线性拟合的方法，拟合时存在少量数据点偏离线性关系而导致参数求解存在误差，从而引起岩石峰值强度的误差；对于岩石的应力-应变曲线峰后应变软化阶段，除高围压(σ3=27.60 MPa)条件下误差较大外，其余围压条件下模型曲线也均与试验数据吻合度较高，分析其误差产生的原因可能是由于岩石试样的不均匀性造成的，因为一般情况下，随着围压的增大，岩石变形特征由脆性转化为延性，即峰后岩石应变软化阶段越不明显，甚至可能会出现岩石应变硬化特征[29]，岩石的应力-应变曲线上表现为峰后阶段曲线斜率总体减小，曲线趋于平缓，而观察该组试验数据可知，前4个围压条件下试验结果表现的正是这种特性，至σ3=27.60 MPa围压时，岩石反而向脆性变形趋势转变，相反，该高围压条件下本文模型曲线表现出岩石延性变形趋势，符合一般规律。总体来说，本文模型能够充分地反映岩石变形破坏的过程，具有可靠性。

3 讨 论

3.1 Weibull分布函数参数的物理力学意义

本文模型中常规岩石力学参数E、μ、G、φ13物理力学意义已经非常明确，这里仅讨论Weibull分布函数的两个参数m和F0的物理力学意义。以围压σ3=6.90 MPa条件下的模型为例，固定F0不变，仅变化m时，可得到一系列岩石应力-应变曲线见图3；同样地，固定m不变，仅变化F0时，可得到一系列岩石应力-应变曲线见图4。

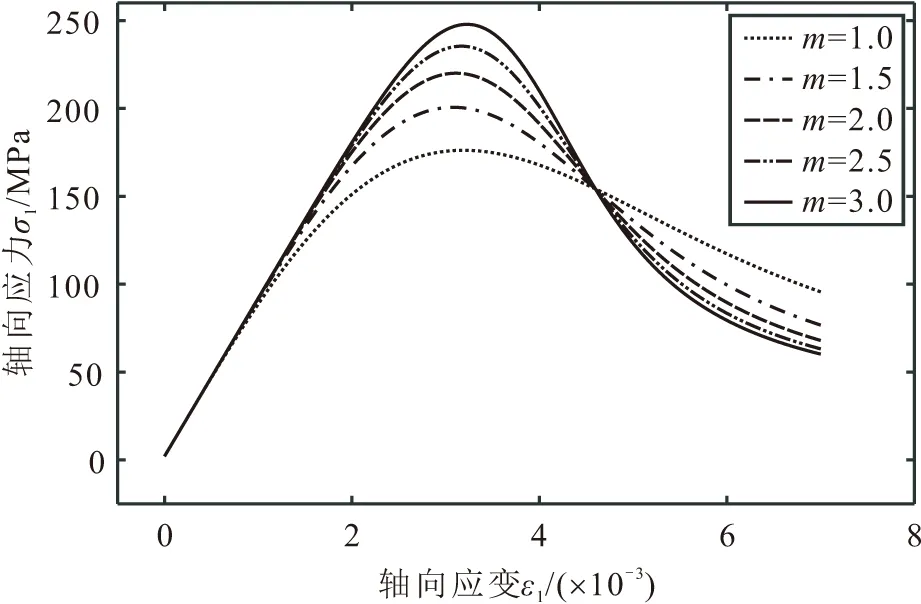
图3 不同m下的岩石应力-应变曲线(σ3=6.90 MPa)Fig.3 Rock stress-strain curves under various m (σ3=6.90 MPa)

由图3可见，随着m值的增大，岩石的峰值强度呈现明显增加的趋势，岩石的应力-应变曲线呈“收缩”形式，岩石强度在达到峰值强度后衰减得更快，反映的是岩石脆性变形程度更大，应变软化现象更加明显。因此，可以认为m是反映岩石脆性变形程度的一个物理量。

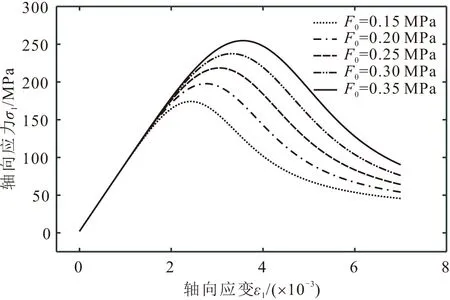
图4 不同F0下的岩石应力-应变曲线(σ3=6.90 MPa)Fig.4 Rock stress-strain curves under various F0 (σ3=6.90 MPa)

由图4可见，随着F0的增大，岩石的峰值强度和残余强度均增大。因此，可以认为F0是反映岩石强度水平的一个物理量。

进一步地，通过分析表1可以发现，Weibull分布函数的参数m和F0是随围压σ3而发生变化的，从这一角度也可以得出围压条件综合影响着岩石的脆性变形程度和强度水平；同时，根据表1可以得出参数m和F0与围压σ3之间的关系，本文采用二次多项式对其关系进行拟合，其拟合结果见图5和图6。

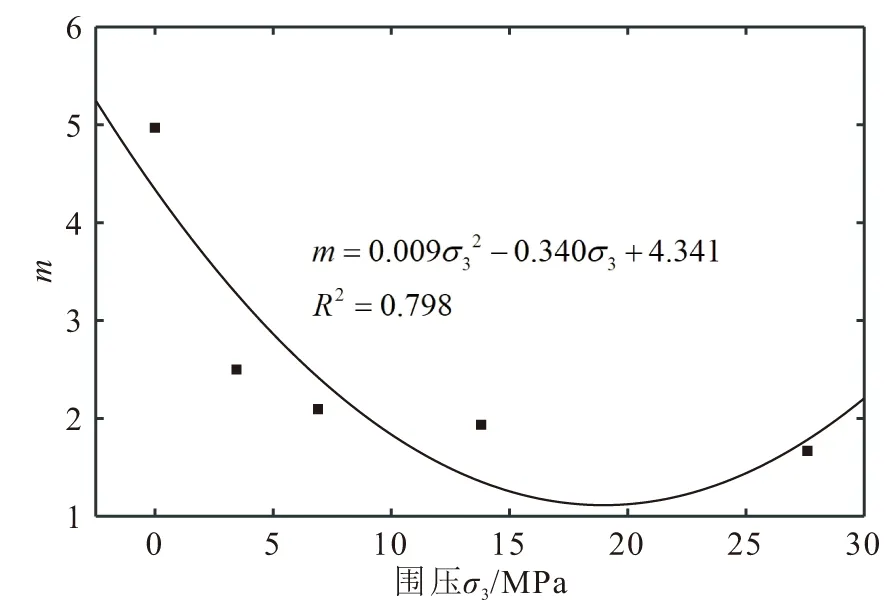
图5 参数m与围压σ3的拟合关系曲线Fig.5 Fitting relationship curve between m and confining pressure σ3

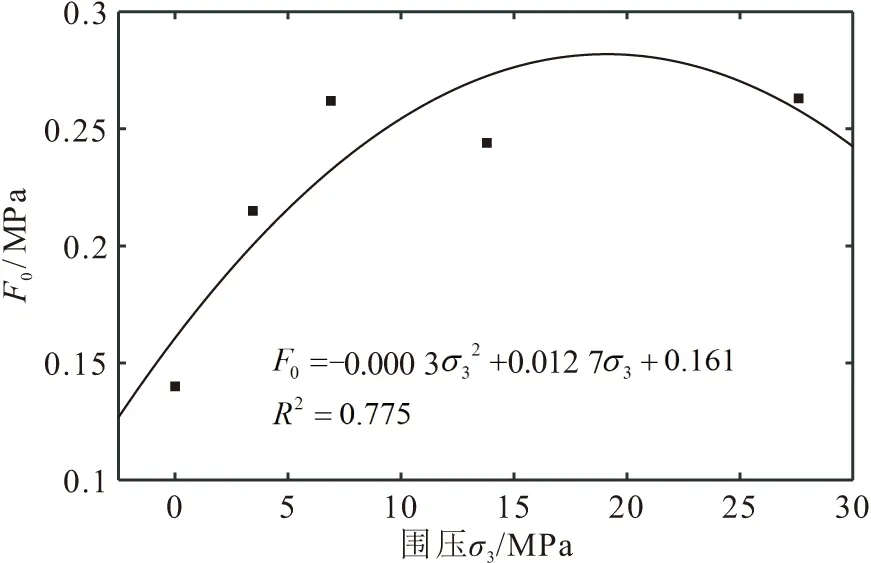
图6 参数F0与围压σ3的拟合关系曲线Fig.6 Fitting relationship curve between F0 and confining pressure σ3

由图5和图6可见，Weibull分布函数的参数m和F0均与围压σ3具有一定的非线性关系，即随着围压σ3的增大，参数m大致呈先减小后略增大的趋势，参数F0呈先增大后略减小的趋势,这同时也说明了围压条件综合影响着岩石的脆性变形程度和强度水平。

3.2 任意围压条件下岩石应力-应变曲线的模拟

上述对给定试验围压条件下岩石的应力-应变曲线进行了模拟，进一步地基于有限数量的三轴压缩试验，利用本文模型也可以获取任意围压条件下岩石的应力-应变曲线。具体方法如下：首先，将任意设定的围压代入图5和图6中的参数与围压之间的关系式中求取参数m和F0；然后，将求取的参数和公式(20)一同代入公式(8)中，即可获得该围压条件下的岩石损伤本构关系方程式；最后，以5个围压水平为例，利用本文模型得到相应的岩石应力-应变曲线，见图7。

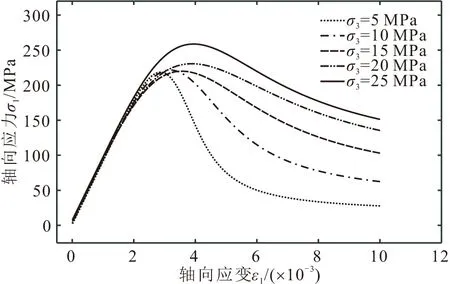
图7 任意围压条件下岩石的应力-应变曲线Fig.7 Rock stress-strain curves under various confining pressures

由图7可见，本文模型能够反映岩石变形破坏过程中的几大典型特性：①岩石应力-应变曲线峰前弹性变形阶段基本不随围压变化而变化，即岩石的弹性模量基本不受围压的影响；②随着围压的增大，岩石的变形特性由脆性转为延性；③随着围压的增大，岩石强度增大。因此，本文模型具有可靠性和实用性。

4 结 论

本文从能量角度出发，引入统计损伤理论，假定岩石微元强度服从Weibull分布，并基于三剪能量屈服准则构建了岩石的微元强度，进而建立了基于三剪能量屈服准则的应变软化岩石的统计损伤本构模型，主要得到了以下结论：

(1) 从能量角度建立的岩石统计损伤本构模型意义更加明确。

(2) 通过一组岩石三轴压缩试验数据验证，本文建立的基于三剪能量屈服准则的应变软化岩石统计损伤本构模型能够反映岩石变形破坏过程中的典型特性，表明本文模型具有可靠性。

(3) 本文模型中各参数的物理力学意义明确，模型中特有的参数m反映的是岩石的脆性变形特性，F0反映的是岩石的强度水平。

(4) 本文模型能够获取任意围压条件下岩石的应力-应变曲线，具有一定的实用性。