算术平均半亚式期权的快速定价算法
陈 聪,唐亚勇
(四川大学数学学院,成都 610064)
1 引 言
期权是一种选择权,即投资者在支付一定的权利金后拥有在预定日期(到期日)以合约中规定的价格(敲定价)买卖相应数量资产的权利.按照权利的差异,期权可以分为看涨期权与看跌期权;按照行权方式的不同,则可以分为欧式期权、美式期权与亚式期权.
在欧式期权中,投资者可以在到期日按照敲定价进行交易.Black和Scholes于1973年首次提出了欧式期权定价公式[1].以看涨期权为例,其定价公式为:
C(S,K,T,σ,r)=SN(d1)-e-rTKN(d2)
(1)
其中,C为看涨期权价格,S为行情价(标的在合约签订当日的开盘价或收盘价),K为敲定价,T为有效期,σ为波动率,r为无风险利率,

由于不同的搅拌时间会影响亚铁离子和铁离子的沉降量及亚铁离子的氧化,故进行搅拌时间的影响试验。试验条件为:Fe2+浓度为0.021 mol/L,温度为60℃,氨水浓度1.0 mol/L,其结果见图6。
在实际应用中,对亚式期权及半亚式期权定价的研究主要有两个方面.其一是利用以蒙特卡洛方法为基础的模拟算法进行定价,再通过控制变量技术、并行计算等方法对模型进行改进.该方法虽然得到的近似定价精度较高,但其计算时间较长[5-7].其二是对期权所满足的偏微分方程求数值解,得到期权的近似定价.该类方法的计算时间较少,但部分PDE方法得到的近似的定价精度无法保证[8-10].
电视节目与画面后期制作涉及的内容和形式相对比较复杂,媒介工作者以及节目制作工作人员和剪辑人员必须充分考虑各类影响要素,了解后期画面制作的相关要求,积极实现不同环节之间的紧密联系和互动,更好地体现不同电视节目制作的内涵以及价值。
本文针对半亚式期权的特点,对期权的波动期和采价期分别采用改进的蒙特卡洛法和矩近似解析法,结合模拟算法与PDE方法,得到了算术平均半亚式期权定价的近似半解析法.在保证精度的前提下,本文将定价的计算时间减少为蒙特卡洛法的7%.然后,本文利用对偶变量技术改进该方法进一步减少了计算时间.
2 改进的蒙特卡洛方法
假设行情价S(t)符合初值为S(0)的几何布朗运动,其中
S(t)=S(0)eX(t),
对于离散的价格{S(n)},存在以下递推关系,
京秦高速公路从北京六环到三河最东部的蒋福山收费站,约44公里,实现了高速公路直达。从燕郊出发行驶京秦高速公路到北京六环,仅有6公里,只需5分钟。
(2)
其中,Δt为n时刻与n-1时刻的时间差,{ξn}是一组相互独立且服从标准正态分布的随机变量.根据上述递推关系可以得到如下欧式期权定价的蒙特卡洛算法.
算法2.1
建立信息发布平台,采用大数据、互联网等技术,将近3-5年内可转移转化的科研成果、专利等信息经过整合后汇集至信息平台。将信息平台推广至企业,企业可以查看最新的科研成果,也可发布近期需求。利用大数据等技术将双方信息进行匹配,匹配度高的需要重点关注、重点规划,进行转化。定期开展调研交流、成果展示活动,或聘请一些企业家顾问,打破壁垒,充分了解市场的需求,使高校和企业的信息充分交流互通。
Step 1:输入S、K、T、σ、r、m,其中m为模拟次数;
Step 2:生成m个服从标准正态分布的T维列向量ai,以ai为列构成矩阵Am×T,令i=1;
隔天,王祥按照老道的吩咐扛着自己的一袋玉器再次踏进古玩市场,老道马上迎了过来,并把王祥带到了一个摊位,虽然同样是地摊,但是在古玩市场里面,怎么看都正规了不少。
Step 3:从S(0)=S出发,按照公式
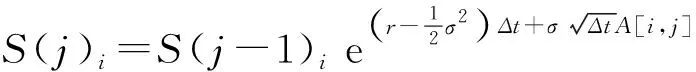
生成序列{S(j)i},其中1≤j≤T,Δt=1∕252(设一年有252个交易日),A[i,j]代表矩阵A第i行、第j列的元素;
造成这种现象的原因有二:1)我国大学开设的专业课程将重心放在理论知识、专业技能的培训上,并未涉及礼仪教育;2)很多德育教育者觉得礼仪教育无关紧要,对此处于盲区。两个方面的原因造成了当今礼仪教育意识缺乏的大环境,有些大学生甚至有步入大学只需学好专业知识,其余无关紧要的想法。因此,若要加强大学生礼仪培育就必须将其引入课堂,引发重视。
Step 5:当i≤m时,返回Step 3;
算法2.2
在欧式期权定价中,我们只需要T时刻的价格S(T),因而蒙特卡洛法模拟的每条价格路径的前(T-1)个价格都是未利用的.为减少蒙特卡洛法定价的计算时间,我们考虑直接在每次路径模拟时生成价格S(T).
由式(2)可以得出
这就是我们的“大嗓门”班长,可是她说,在家里邻居都说她像林黛玉呢。原来,她的大嗓门是为了我们这个班集体。
由上式可得
(3)
由于{ξn}是独立同分布标准正态分布的随机变量,我们有
即
ξ
代入式(3)可以得
总体而言,气象导航能充分利用有利的天气和海洋环境,如顺风、顺浪、顺流等,以此来提高船速或使船舶失速降到最低限度,以达到缩短航时,降低营运成本和提高经济效益的目的。
(4)
根据式(4)可以直接由S(0)生成S(T),进而得到如下欧式期权定价的改进蒙特卡洛算法.
Step 1:输入S、K、T、σ、r、m;
Step 2:生成1个服从标准正态分布的T维列向量a,将a记为矩阵Am×1,令i=1;
Step 5:计算Ci=max{avei-K,0},完成一次模拟,i=i+1;
生成S(T)i;
Step 4:计算Ci=max{S(T)i-K,0},完成一次模拟,i=i+1;
Step 5:当i≤m时,返回Step 3;
采用目视方法(可利用放大镜、内窥镜、焊缝检查尺)检查本体结构,几何尺寸,表面情况(如裂纹、腐蚀、泄露、变形等)。着重检查空气储罐内壁的腐蚀情况、地脚螺栓和排污阀的使用状况。对于内壁点腐蚀,应测量腐蚀深度、面积、长度;对于均匀腐蚀,应测量腐蚀区域的厚度,并进行强度校核。地脚螺栓未按照要求进行安装的要责令使用单位安装到位。检查排污阀腐蚀情况,着重检验排污阀的泄露情况、通畅情况和定期排污情况。
例如,设定T=63,σ=0.2,r=0.03,期权类型为看涨期权,我们分别对实值期权(S=100,K=90)、平值期权(S=100,K=100)和虚值期权(S=100,K=110)进行数值算例模拟.下面我们来比较欧式期权定价的BS公式法(EBS,式(1))、蒙特卡洛法(EMC算法2.1)和改进蒙特卡洛法(EIMC算法2.2),其中蒙特卡洛法的期权价格和计算时间为运行1 000次程序后取均值,单次模拟次数为105次,基准价格为EBS算法的价格.程序运行的软件环境为Win10+Python 3.7,硬件环境为Intel Core i5-8300H,结果见表1.
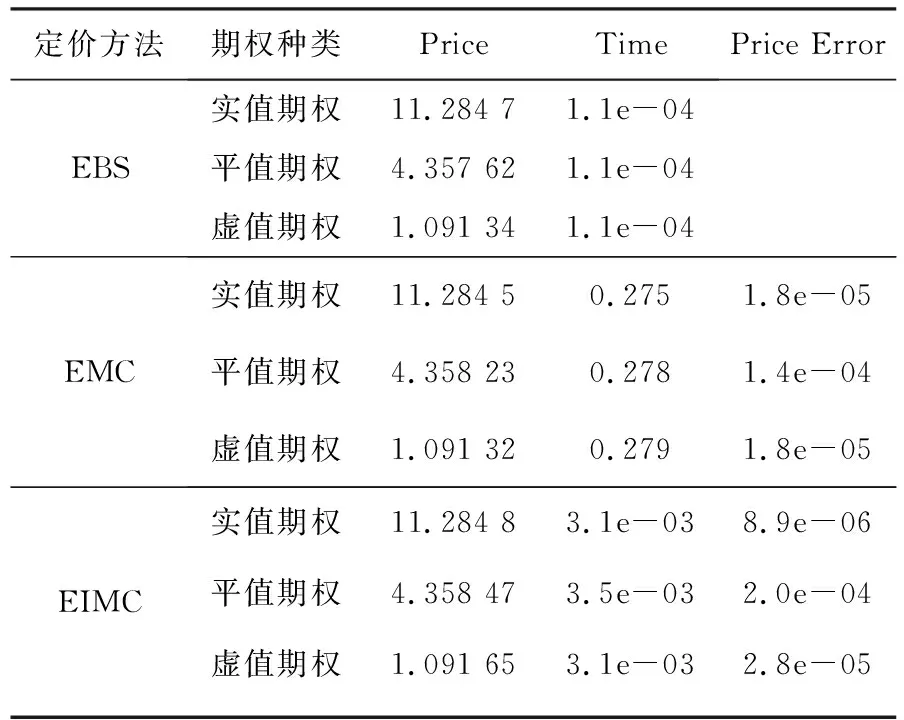
表1 EBS、EMC、EIMC算法的算例比较
可以看出,对实值期权、平值期权及虚值期权,蒙特卡洛法和改进的蒙特卡洛法对比公式法的价格误差都极小.因而在价格没有解析表达式的期权(如美式期权、算术平均亚式期权)定价过程中,我们可以使用蒙特卡洛法进行定价,近似地得到真实价格.同时,改进蒙特卡洛法的计算时间仅为蒙特卡洛法的1%,效率较高.
算术平均亚式期权需要计算[0,T]时间段内每一时刻价格的平均值作为行情价,一般采用蒙特卡洛法来进行定价,算法如下[11-12].
算法3.1
Step 1:输入S、K、T、σ、r、m;
式中:mw为热水器的进水流量,L/min;Cw为水的比热容,kJ/(kg·K);T为t时刻管内热水的实际温度(数值上应等于出口温度Tout),℃;Ct为热水器系统的热容,kJ/K;Gw为稳定状态下的燃气进气流量,m3/s;H为燃气高热值,H=39.82 MJ/m3;ξss为稳定状态下的热效率,取热水器1级能效标准,ξss=98%。
Step 2:生成m个服从标准正态分布的T维列向量ai,以ai为列,构成矩阵Am×T,令i=1;
很多企业的内控制度并不健全,领导及员工的内部控制意识淡薄。这主要表现为:①有的企业没有设置内部控制制度。②有的企业虽然制定了内部控制制度,但该制度存在缺陷,缺乏可操作性。③有的企业设定了有效的内控制度,但是员工并没有按制度执行。
数学课程标准(2011年版)关于课程具体目标“知识与技能”的表述中,出现了大量“经历过程”的描述,这正是对实践操作的模型理解的体验,让学生更深入理解知识的建构关系。经历图形的抽象、分类、性质探讨、运动、位置确定等过程,这些都是“知识与技能”目标中的“过程性目标”。学生对基础知识的理解,应该尽量达到扎实的程度,应该在知识的应用中不断巩固和深化,从而真正掌握这些基础知识。
Step 3:按照算法2.1的Step 3,生成序列{S(j)i};
Step4:计算序列{S(j)}i的算术平均值avei;
Step 3:从S(0)=S出发,按照公式
从实践中看,随着城市化的快速发展,城市供水设施完全由政府承担是背不了,也是背不起的。因此,可逐步尝试由国有资产管理局或国有资产经营公司负责对供水企业国有资产进行的监管和水务局对供水企业进行的行业监督管理相结合,用委托人与被委托人之间的资产纽带关系取代传统体制下政府与企业之间的行政隶属关系,供水企业在遵循严格统一的行业监管条件下,成为享有自主经营权的法人实体。政府不再直接干预企业的日常生产经营活动,企业按照市场经济原则开展生产经营活动,从而实现供水企业经营机制的根本性转换。
Step 6:当i≤m时,返回Step 3;
Step 4:取序列{S(j)i}的最后一个数S(T)i,计算Ci=max{S(T)i-K,0},完成一次模拟,i=i+1;
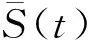
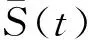
CAMA(S,K,T,σ,r)=
(5)
其中
此外,亚式期权矩近似解析法的价格可直接按照式(5)进行计算,算法不再给出.
下面我们再给出一个数值算例.设定T=63,σ=0.2,r=0.03,期权类型为看涨期权.我们分别对实值期权、平值期权和虚值期权进行数值算例模拟,以比较亚式期权定价的蒙特卡洛法(AMC算法3.1)和矩近似解析法(AMA,式(5)),其中蒙特卡洛法的期权价格和计算时间为运行103次程序后取均值,单次模拟次数为105,基准价格设为AMC算法的价格(由第2节的结论,近似认为105次蒙特卡洛法的期权价格为真实价格),结果见表2.

表2 AMC与AMA的算例比较
由表2可以看出,对于实值期权和平值期权,矩近似解析法相较蒙特卡洛法的误差分别为0.6‰和7‰,处于可接受的范围内;对于虚值期权,误差在9%左右,偏差较大,但矩近似解析法的计算时间仅为蒙特卡洛法的0.4‰,提升效果明显.鉴于在场外期权市场中虚值期权交易较少,在实际运用中可以考虑用矩近似解析法来进行亚式期权快速定价.
4 算术平均半亚式期权定价的快速算法
按照半亚式期权的定义,我们可以将[0,T]时间段分为[0,T′]和[T′,T]两个时间段,其中[0,T′]时间段为波动期,行情价S(t)符合初值为S(0)的几何布朗运动;[T′,T]时间段为采价期,行情价S(t)符合初值为S(T′)的几何布朗运动.
在波动期内,我们采用改进蒙特卡洛法得到价格S(T′)i,随后对每一个价格S(T′)i用式(5)计算得到CAMA(S(T′)i,K,T-T′,σ,r),即在采价期内可将其看成S(0)′=S(T′)i,K=K,T=T-T′,σ=σ,r=r的一次亚式期权定价.对CAMA(S(T′)i,K,T-T′,σ,r)进行贴现后可得到S(0)时刻的半亚式期权价值,即
e-rT′CAMA(S(T′)i,K,T-T′,σ,r)
(6)
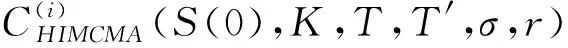
算法4.1结合改进蒙特卡洛法与矩近似解析法的近似半解析法(HIMCMA)
Step 1:输入S、K、T、σ、r、m;
Step 2:生成1个服从标准正态分布的T维列向量a,将a记为矩阵Am×1,令i=1;
Step 3:按照算法2.2的Step 4生成序列S(T′)i;
Step 5:当i≤m时,返回Step 3;
…,
由半亚式期权定价的近似半解析法,在采价期内采用矩近似解析法进行直接计算,在波动期内采用改进蒙特卡洛法进行价格路径模拟.为减少定价的计算时间,我们可以考虑在波动期内采用对偶变量技术[14-16],在保证方差不变的前提下减少模拟次数,算法如下.
算法4.2对偶近似半解析法(HIMCMAA)
Step 1:输入S、K、T、σ、r、m、n,其中n为蒙特卡洛模拟次数减少系数,即蒙特卡洛模拟总次数为2m/n;

Step 4:按照算法4.1的Step 3和Step 4完成一次模拟,i=i+1;
Step5:当i≤m时,返回Step 4;
下面我们给出一个数值算例.设定T=63,T′=21,σ=0.2,r=0.03,期权类型为看涨期权.我们分别对实值期权、平值期权和虚值期权进行数值算例模拟,以比较半亚式期权定价的蒙特卡洛法(HMC)、近似半解析法(HIMCMA)和对偶近似半解析法(HIMCMAA,n=2,4,8)的计算效率.其中,期权价格和计算时间为运行103次程序后取均值,单次模拟次数为105,基准价格设为HMC算法的价格.结果见表3.

表3 HMC及HIMCMA、HIMCMAA(n=2,4,8)算法的算例比较
可以看出,对于实值期权和平值期权,近似半解析法相较于蒙特卡洛法的误差分别为1‰和5‰左右,处于可接受的范围内;对于虚值期权,误差在1.6%左右,偏差较大.但是,鉴于近似半解析法的计算时间为蒙特卡洛法的7%左右,效率提升明显,在实际运用中可以考虑利用近似半解析法进行半亚式期权快速定价.同时,我们还发现,随着n的增大,模拟次数不断减少,HIMCMAA算法的计算时间也不断减小,方差缓慢增大,价格误差则几乎没有变化.因此,在实际运用中可以比较近似半解析法和对偶近似半解析法的方差来确定合适的n,以保证在方差尽可能不变的前提下减少计算时间.
本文旨在减少算术平均半亚式期权定价的计算时间.首先,根据行情价服从几何布朗运动的理论假设,本文提出了改进蒙特卡洛法.随后,对半亚式期权的波动期和采价期分别采用改进蒙特卡洛法和矩近似解析法,本文提出了近似半解析法.数值算例比较发现,在保证精度的前提下,近似半解析法的计算时间大幅少于传统蒙特卡洛法.此外,本文利用对偶变量技术改进近似半解析法提出了对偶近似半解析法,在误差可接受的情况下进一步减少计算时间.

