基于遗传算法的改进时序预测模型研究

李思莉，杨井荣

(成都理工大学 工程技术学院 电子信息与计算机工程系，四川 乐山 614000)

0 引 言

互联网技术的发展带来了电子商务等业务的迅猛发展，用户请求和互联网环境越来越复杂，服务器负载急剧增加，为互联网应用的高可用性、高性能和服务质量带来了严峻的挑战。传统的Web集群模式由于集群规模固定的问题，无法应对突发性访问激增带来的负载压力。

云计算技术的出现使得集群规模可以随工作压力变化而动态调整，资源按需获取成为可能。云计算中的弹性伸缩是一种云计算系统根据系统需求变化而自动调整的技术。它能有效提高用户满意度，特别是当系统需求不稳定时，能很好地调度资源，避免资源分配不足或资源浪费。其组织分类如图1所示。

对于资源的伸缩，一般分为水平伸缩和垂直伸缩。在水平伸缩(伸/缩)过程中，以虚拟机为最小资源单位按需要添加或释放虚拟机；在垂直缩放(上/下)过程中，通过改变分配给已经运行的虚拟机的资源来实现，例如增加(或减少)分配的CPU或内存。对于弹性伸缩的实现机制，目前比较流行的是反馈触发策略[1]和提前预测。反馈触发策略是根据一些性能指标和预定义的阈值来触发伸缩，也就是说，系统将根据用户负载是否达到某个确定的阈值来决定增加或减少资源。但是，需要精确的定量值，通常容易出现不确定性[2]。同时，如果用户负载非常不稳定，就会造成系统资源的频繁伸缩，这本身也会给系统带来很大的负担。加之，这种反馈触发策略在资源分配部署过程中存在较大的延时问题，在用户负载大规模增加的情况下，处理能力有限。

图1 弹性云服务组织分类

预测模式以时间序列方法[3]、控制理论[4]、增强学习(RL)[5]和队列模型[6]为主，但单纯的时间序列方法难以预测峰值和工作负载真实变化。队列模型只适用于静态环境。此外，队列模型的现有方法(QM)对弹性系统有不切实际的假设，并且这些假设在云计算环境中并不适用，因为在云环境中，动态工作负载是一种常态。

该文利用遗传算法改进时序预测模型，结合当前资源使用率，对未来趋势进行预测，从而实现了资源动态快速伸缩。通过实验表明，该预测模型在同等虚拟用户请求的时序下，虚拟机数量在满足SLA的情况下较少，并且响应速度下降。

1 相关工作

1.1 排队论

排队论是排队等待中的概率处理最优化设计问题。排队论(QT)被广泛用于表示基于internet的应用程序和传统服务器性能指标，如队列长度和平均等待时间请求的时间。云应用程序场景使用一个简单的QM对于在“n”个虚拟机之间分配请求的负载平衡器。现实云环境中的自动缩放问题是通过周期性地改变传入的到达和无限服务器容量的假设。排队理论包括到达过程、排队规则、服务机制，如队列长度和平均等待时间请求的时间。文献[7]中使用排队论对工作负载和服务平均响应时间进行预测，从而实现资源的动态分配。目前，被广泛使用的排队模型是M/M/1和G/G/1[8]，M/M/1将用户服务请求过程看作为是一个参数为λ的泊松流，其中到达时间和服务时间是基于指数分布的，而G/G/1到达时间和服务时间是基于一般分布的,这种模型最大的问题是当面对峰值负载时，可能造成大量的资源浪费。排队论适用于结构相对固定的系统，如果系统结构发生变化，需要重新建模。因此，排队论在云计算资源动态伸缩的管理中代价很高，通常不是一个太好的选择。

1.2 时间序列分析预测模型

基于时间序列分析的弹性策略是实现资源弹性管理的常用方法。它能够预测应用程序的未来需求，所以通常用来提前申请资源，从而有效避免了在虚拟机启动和应用程序部署上花费时间。这一策略具有巨大的潜力，在金融、工程、经济和生物信息学等领域有着广泛的应用。其独特的特性也决定了该方法同样适用于云计算环境下的资源预测。

目前，时间序列预测分析方法的主要模型有朴素模型(Native)、自回归预测模型(AR)、自回归滑动平均模型(ARMA)、差分自回归滑动平均模型(ARIMA)以及扩展指数平滑模型(ETS)和神经网络预测模型等[7]。朴素模型非常简单，它假设最后一次的观测值将出现在下一个时间间隔内。这个模型只需要单个时间点序列。

自回归预测模型可以根据最近几个时间段的负载值预测下一个时刻的负载。其线性表达式为：

yt=c+φ1yt-1+φ2yt-2+…+

φpyt-p+εt

(1)

其中，c是常量，εt是独立的误差项，φ1是自相关系数，该系数如果小于0.5，其预测结果将极不准确。

自回归滑动平均模型ARMA(p,q)包含了两个多项式的平稳随机过程，一个用于自回归，另一个用于移动平均线。其模型可以表示为：

(2)

其中，p和q是模型的自回归阶数和移动平均阶数；φ和θ是不为零的待定系数；εt是独立的误差项；Xt代表平稳、正态、零均值的时间序列。ARMA模型适用于预测在一定趋势内变化的时间序列。

差分自回归滑动平均模型ARIMA(p,d,q)是ARMA模型的扩展，它不直接考虑其他相关随机变量的变化，其模型可以表示为：

(3)

其中，p是自回归项数，q是滑动平均项数，d是使之成为平稳序列所做的差分次数(阶数)。该模型的缺点是参数选取困难。

神经网络预测模型适用于非线性时间序列的预测，它采用梯度下降法来计算阈值和权值，并通过不断修正网络权值和阈值使误差函数沿负梯度方向下降，逼近期望输出。误差函数表达式为：

(4)

其中，ti为期望的输出，oi为网络实际输出。但是，神经网络预测模型容易导致神经网络陷入局部最优解，降低预测精度。

1.3 时间序列预测算法

目前，时间序列预测算法主要以差分自回归滑动模型(ARIMA)[9]为基础，这些算法对于时间有较强依赖性的线性数据有较好的预测效果，但对于非线性数据，如果数据波动过大，将对非平稳序列差分进行平稳化处理，变成平稳序列之后再进行移动回归，这将会导致预测误差增大。在实际云环境中，单一的ARIMA算法很难准确预测工作负载。因此，目前有些研究人员已经对ARIMA算法进行了改进，如文献[10]用傅里叶变换提高预测准确度；文献[11]中引入平均误差提高预测精确度；文献[12]对下一个预测周期进行预测误差补偿，防止误差进一步扩大；文献[13]对历史窗口大小进行动态调整。这些算法是以ARIMA算法为基础进行的改进，对提高预测准确度有一定的帮助。

2 改进的时序预测算法

2.1 资源分配弹性伸缩框架

由于并发或重复的请求是从多个客户机发出的，因此到达间隔时间成为一个随机变量，又由于到达的请求遵循具有无限计算能力的泊松过程，所以系统使用M/M/m队列模型来处理到达的服务请求，m是提供的服务器数量。仿真结果表明，稳态下队列长度等待的平均时间会随平均间隔时间的增加而降低，如果增加服务器m(虚拟机)的数量，等待时间会降低。但是，在云计算环境下，需要通过负载平衡策略和时间预测算法计算出在不违反SLA原则的基础上，最小化资源的占用率，即m的值。其框架示意图如图2所示。

图2 资源分配弹性伸缩框架

从图2可以看出，弹性分配策略主要分为两个阶段，第一阶段负责预测下一个时间间隔的需求，第二阶段根据改进的基于时间序列的算法求取最小资源数，动态调整调度资源。

2.2 改进的基于遗传算法时序的预测算法GA-ARIMA

本算法是对ARIMA基本算法的改进，因此在设计时首先使用了arima()函数创建自回归模型，接着使用auto.arima()函数根据确定的时间间隔调整参数，最后使用ets()函数调整平滑指数，使之与数据的拟合度最高。其具体算法伪代码如下：

input:client request //用户请求

output:next point //下一个时间间隔需求预测

1:init();

2:foreach timeInterval do

3:TS<-read(information); //将用户请求转换为时序

4: foreach m do

5:value[m]<-predictAhead(m);

6: end

7:nextValue<-UsingPerviousValue(value);

8:end

该算法首先完成初始化的工作，然后对于每个时间间隔(这个值可以设定)，将用户请求(可以多个，高并发)转换为时序，根据时序选择适用的参数及模型，得到需求值。最后根据前一个需求值等到下一个预测值。

UsingPerviousValue函数需要用到遗传算法[14]，该算法模拟达尔文的进化论，其具体描述如下所示：

input：perviousValue

output：nextValue

1:Initializate ();

2:While(not Terminate-Condition) do

3:evalPopulation();

4:select();

5:crossSelected();

6:mutateResultValue();

7:evaluateResultValue();

8:updatePopulation();

9:end

10:outputNextValue;

11:end

2.3 资源分配

根据2.2描述的预测算法得到的结果，使用M/M/m队列模型[15]来分配资源，其系统资源利用率根据等式(5)来计算。

(5)

其中，ρ是系统利用率，λ是到达率，μ为处理率，m为服务器的数量。文中的目标是找到满足用户需求的m的最小值。因此变换式(5)得：

(6)

M/M/m模型中，系统利用率ρ和响应时间t密切相关，响应时间t计算如下：

(7)

将式(5)和式(7)带入式(6)得：

(8)

根据式(8)就可以计算出所需资源，要使m值最优，采用如下算法：

输入：预测值(算法2的结果)

输出：m

初始化;

1：foreach(TS) do

2：λ<-getForecastPrevious(model);

3：μ<- getProcessingRate();

4：sla<-getMaxRT();

5：m<-calculateResources(λ,μ,sla);

6：end

通过预测获得了下一个时序的到达率后，每个虚拟机和最大响应时间的μ值可以计算出来，最后带入式(8)得m的值。

3 仿真实验分析

为了验证提出的基于遗传算法改进时序预测的云计算弹性伸缩策略的有效性，利用基于OpenStack[16]开源项目搭建云平台，将CPU需求(虚拟机数量)作为实验数据，在Matlab上进行仿真，初始参数设置如表1所示。

表1 参数设置

图3模拟了400秒内虚拟用户的随机请求时序。

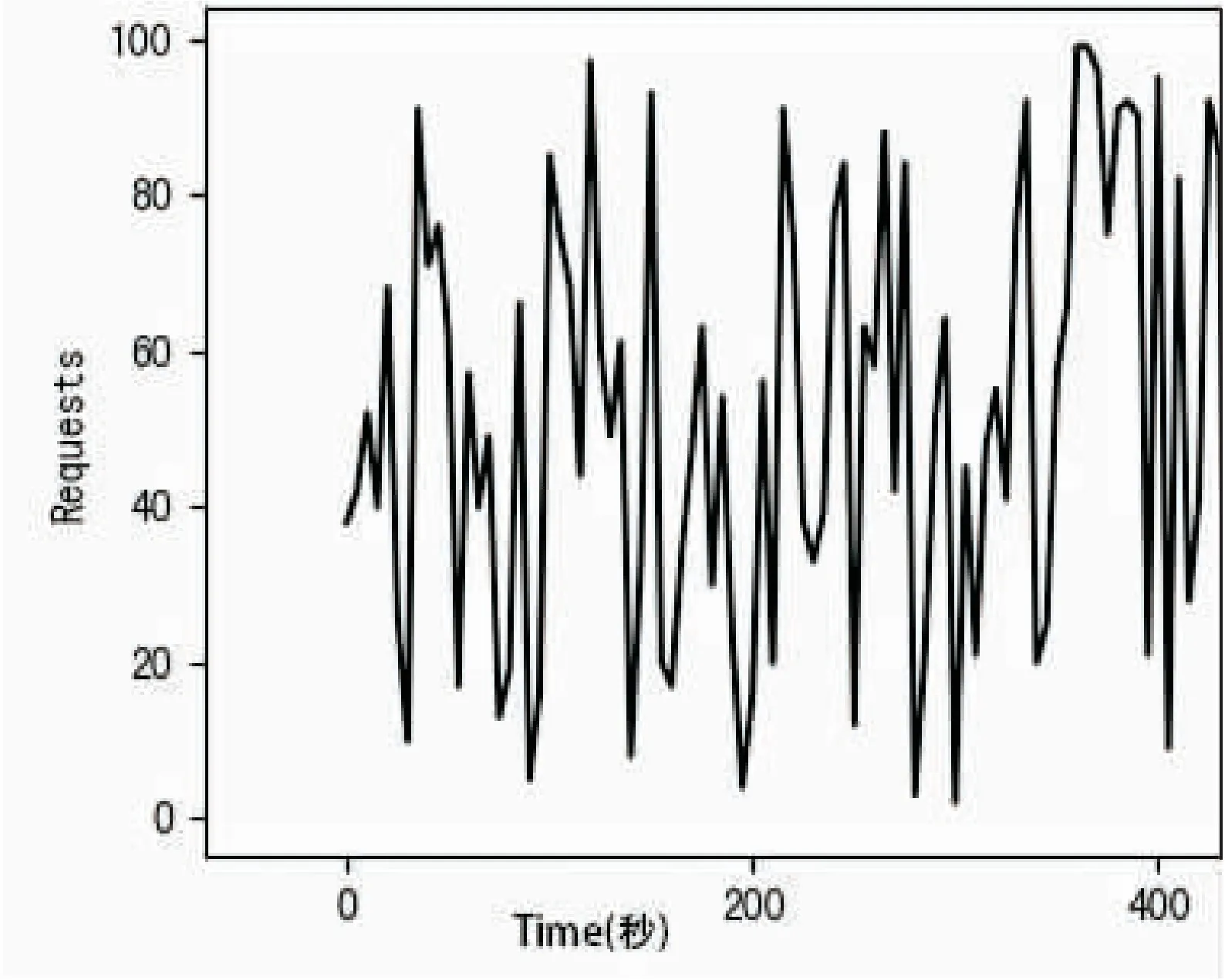
图3 时序图

根据计算公式和实验数据得出的误差率如表2所示。

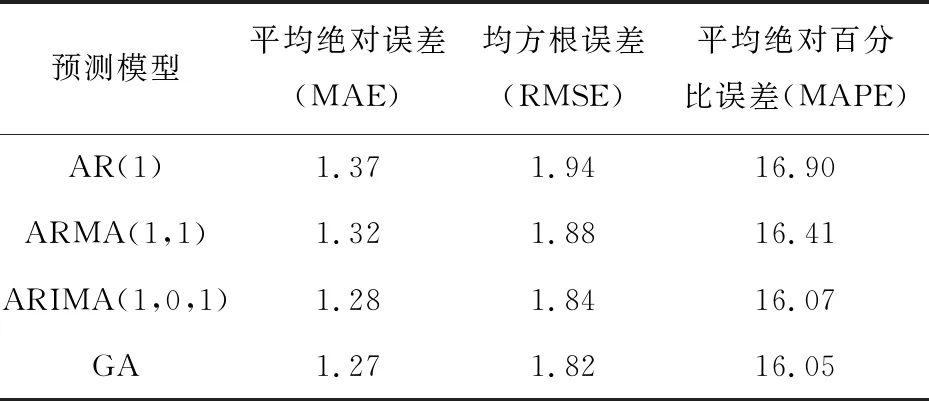
表2 各模型误差值

由实验结果可以看出，在同一时序下，利用遗传算法改进的预测模式平均绝对误差、均方根误差等都有一定程度的降低。

根据式(8)计算所需虚拟机数量，在一周的时间内，相同负载下的不同模型实验结果如图4所示。

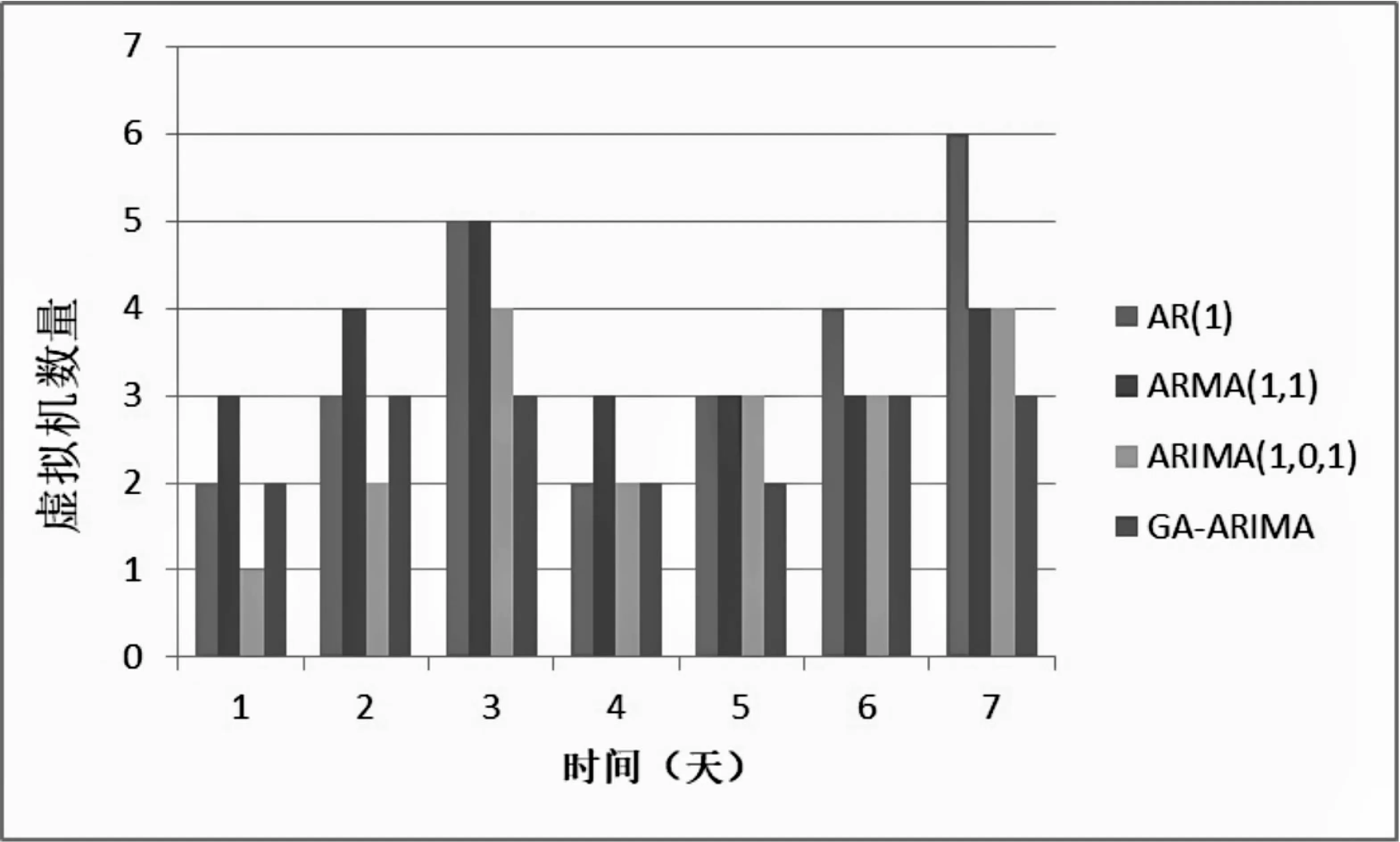
图4 虚拟机数量对比

4 结束语

首先介绍了云计算弹性伸缩策略的必要性和现存策略的弊端，对目前现有的预测模型进行了相关的介绍，指出它们的优劣。在此基础上利用遗传算法对ARIMA模型进行改进，并对未来一段时间的虚拟机需求做预测，从而决定是否需要伸缩。通过实验表明，提出的基于遗传算法的预测模型在一定程度上减少了CPU使用率，减少了预测误差，有一定的优越性。