基于组件自动机的概率连续行为的形式化模型

卜星晨，曹子宁，王福俊

(南京航空航天大学 计算机科学与技术学院，江苏 南京 211106)

0 引 言

基于组件的开发技术正逐渐应用到信息物理融合系统(CPS)[1-2]的开发过程中。现已有许多基于组件的软件系统开始应用到航空航天、军事过程控制等领域当中，这些领域往往对系统的正确性和可靠性要求比较高。系统执行过程中的一个小小的错误都有可能导致巨大的灾难。而这类系统往往同时具有连续性和离散性，且每个子系统之间存在着频繁的数据通信，因而给这类系统的准确建模带来了一定的困难。

基于组件[3-4]的开发技术是一种将系统组件化、然后再将组件化后的系统组件进行组合的技术。采用形式化的方法[5]对CPS进行建模与验证，能够很好地保证系统的正确性和安全性。形式化的验证过程一般采用形式化建模语言对系统进行建模，采用逻辑语言刻画所要验证的性质，最后使用形式化验证工具自动地对模型和逻辑规约进行验证。文献[6]指出在基于组件的开发过程中引入形式化的建模方法和自动化验证技术，是一个重要的研究方向。

该文针对CPS，在组件自动机的基础上扩展了概率、连续行为特性，提出了概率混成组件交互自动机，并给出了具体的定义及其进行组合验证的算法。提出的概率混成组件交互自动机不仅能够描述组件之间的交互行为，还能能够清楚地刻画出系统的体系机构以及组件内的连续动态性和状态迁移上的概率选择性。

1 背景和动机

CPS是一种将计算过程与物理过程组合在一起的实时反应式系统。其最主要的特征是系统中同时包含离散性和连续性。CPS本身是一种基于组件的系统，每一个软件实体或者物理设备都能够独立运行，每个子系统之间可以通过信号的传输实现相互合作的功能。

现已有许多能够对混成系统进行建模的形式化方法，如混成自动机[7-8]和混成I/O自动机[9-10]。然而混成I/O自动机是输入使能的，即混成I/O自动机中的每一个状态都必须能够接收所有可能的输入动作，而混成自动机并不能够将组件之间的通信组合方式进行准确建模。因此，需要一种新的形式化建模方法对CPS进行建模。

组件交互行为的建模方法可以分为两大类：基于进程代数的方法和基于自动机的方法。基于进程代数的方法主要使用CSP/Timed CSP、Pi演算、CCS/Timed CCS等进程代数语言进行建模。基于自动机的方法主要使用接口自动机[11]、I/O自动机、时间自动机[12]以及时间I/O自动机[13]进行建模。组件交互自动机[14-16]在自动机的基础上根据进程代数的思想扩充了组件之间交互行为的描述，使其能够保留组件之间的交互属性。

1.1 组件交互自动机

组件交互自动机是一种非确定的自动机，其中每一个迁移动作都标注为输入、输出或者内部动作。输入(输出)动作与接收(发出)该动作的组件相关联。内部动作与动作上同步的两个组件相关联。在组件交互自动机的一次组合过程中，只有两个组件可以进行同步操作。组件交互自动机的定义如下：

定义1：组件交互自动机COIA可以写成元组的形式(Q,Q0,A,Σ,E,H)，其中：

(1)Q表示非空的有限状态集合；

(2)Q0⊆Q表示初始状态集合；

(3)A表示有限动作集，包括输入动作、输出动作、内部动作τ和空动作ε；

(4)Σ表示动作约束符号表的集合，Σ={(C)×A×(C∪(±))}，C表示组件及其接口的名称，C∈N(H)，N(H)表示组件组合过程中涉及到的组件名称的集合，+和-分别表示输入动作和输出动作；

(5)E⊆Q×Σ×Q，表示状态迁移的集合；

(6)H是用来表示组件内部组件组合层次的元组，元组Hi=(ni1,ni2,…,nim)表示组件Hi由m个组件在同一层次上组成而成。括号用来表示组合的层次性，最内层的组件最先进行组合，然后依次向外进行组合。

(A,a,+),(B,a,-),(B,a,A)∈E分别表示输入、输出和内部动作。(A,a,+)表示组件A接收动作a，(B,a,-)表示组件B发送动作请求a，(B,a,A)表示组件B输出动作a，组件A接收到动作a。

1.2 动 机

CPS是基于组件的系统，这为使用COIA对CPS进行建模提供了良好的基础。现有的组件交互自动机只支持离散系统的建模，并不支持概率以及连续行为性质的建模。因此，对组件交互自动机进行了相应的扩展，在组件交互自动机的基础上提出了概率混成组件交互自动机PHCOIA来对CPS进行建模。

2 概率混成组件交互自动机

PHCOIA在COIA的基础上添加了变量集X，变量集X的不同取值表示系统所处的不同状态。PHCOIA在COIA的基础上对状态上的动作变迁，增加了关于变量集合X的约束条件Enab，只有满足了相应的约束条件之后，才能执行动作进行状态变迁。

现实生活中总会存在一些不确定因素对系统的执行造成一定的影响，因此在COIA的状态迁移上添加了概率分布P，表示状态变迁上的不确定选择。除此之外，还定义了赋值函数Fa和流函数F分别表示对状态内变量的赋值操作以及定义状态内变量的变化速率。通过定义不变式I约束每个状态内变量的变化范围。PHCOIA的定义如下：

定义2：PHCOIA可以写成元组的形式(Q,Q0,A,Σ,X,Xinit,Fa,F,Enab,E,I,P,H)，其中：

(1)Q表示非空的有限状态集合；

(2)Q0⊆Q表示初始状态；

(3)A表示有限动作集，包括输入动作Ain、输出动作Aout、内部动作Aint和空动作ε；

(4)Σ表示动作约束符号表的集合， Σ={(C)×A×(C∪(±))}，C∈N(H)；

(5)X表示实值变量的有限集合；

(6)Xinit表示变量集合X在初始状态的取值；

(7)Fa:Q→assign(X)表示赋值函数，用来对状态中的变量进行赋值；

(8)F:Q×|X|→|X|表示状态上变量的流函数，F函数定义了变量的变化率，通常使用变量对时间的一阶导数进行表示；

(9)Enab:Q×Σ→guard表示状态执行动作迁移的谓词条件，guard为变量集合X上的布尔表达式；

(10)E表示状态迁移的集合，E⊆Q×Σ×Q'；

(11)I为状态q⊆Q上的不变式条件，用来限制变量的变化范围，不变式条件通常使用变量集合X上的布尔表达式进行表示；

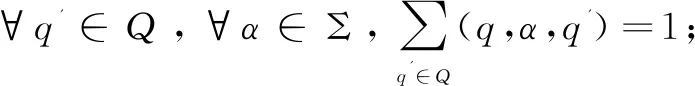
(13)Η是描述该组件内组件组合层次的元组。

3 PHCOIA的迁移系统语义

PHCOIA中的状态由系统当前所处位置q∈Q和变量的取值组合而成。PHCOIA中有两种迁移方式：动作迁移和时间迁移。动作迁移：当状态内的变量值满足相应的谓词条件guard时，当前状态将会执行动作Σ跳转到下一个状态；时间迁移：系统停留在当前位置q，但系统中的变量随着时间的流逝不断地发生变化。时间迁移的边标记为实数值，表示系统在位置q上停留的时间。Δ表示所有迁移边的集合，Δ=Σ∪R≥0。

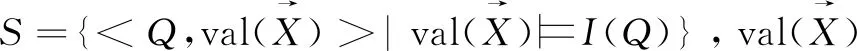
PHCOIA的迁移系统从初始状态S0开始执行，如果当前状态满足动作迁移的使能条件Enab，系统将会根据概率分布P从所有可能的后继状态中选择一个状态进行跳转；如果当前状态不满足变迁的使能条件，状态将会执行时间迁移，状态内的变量根据流函数随着时间的变化而发生变化。

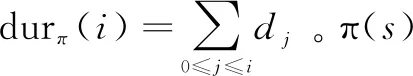
时间延迟只发生在位置上，动作变迁的时间忽略不计。因此，如果不对状态变迁进行进一步的约束，就有可能出现自动机在有限时间内执行无限多动作的情况，即Zeno行为。然而现实生活中这样的情况是不存在的，即不存在可以在有限时间内执行无限多指令的计算机。因此，接下来给出结构良好性标准。

定义4：如果对于TR(M)中的所有状态s，满足∀n∈，∃π∈π(s)，∃i∈，durπ(i)>n，即对于任意给定的时间n∈，总是存在一条从状态s开始的路径π(s)，从状态s到达路径π(s)上某一状态的时间大于n，则称PHCOIA满足结构良好性标准。

该文所定义的PHCOIA不包含齐诺行为。只有满足结构良好性标准的PHCOIA才能进行有效的组件组合。

4 PHCOIA的组合与验证

4.1 PHCOIA组合的相关概念

在交互自动机的组合过程中，需要匹配对应的输入输出动作。在状态的组合过程中，除了需要组合状态内的变量集外，还需要组合状态上的赋值函数、流函数和不变式约束，同时在生成的状态集上生成对应的迁移关系以及对应的概率分布，以构造新的组件自动机。

定义5：如果两个状态内的赋值函数、流函数和不变式约束中出现的变量集合不相交，则称这两个状态可以进行组合。

定义6：PHCOIAM有输出动作(Ci,αi,-)∈ΣM，i∈，PHCOIAN有输入(Ck,αk,+)∈ΣN，k∈。将M和N进行组合，如果αi和αk动作名称相同且输出动作αi前后两个状态可以与输入动作αk前后两个状态分别进行组合，则称输出动作αi与输入动作αk匹配。在不考虑内部动作细节的情况下，内部动作可以简记为(Ci,τ,Ck)。

定义7：D(H)表示组件组合层次的深度。H=(C)，表示H内只有一个元素C，即该组件是一个原子组件，组件的组合深度为1。

定义8 ：PHCOIA的组合S=(Q,Q0,A,Σ,X,Xinit,Fa,F,Enab,E,I,P,H)，是由PHCOIA的集合{Mi=(Qi,Q0i,Ai,Σi,Xi,Xiniti,Fai,Fi,Enabi,Ei,Ii,Pi,Hi)}组合而成，其中：

(1)i∈N且参与组合的组件名称集合{(N(Hi))}互不相交；

(3)动作约束符号Σ⊆{C×A×(C∪(±))}，C∈N(Hi)∪N(Hk)；

(5)Fa,F,I分别为组合后状态上的赋值函数、流函数以及不变式约束；

(6)H为组件内组件组合层次的元组。

在自动机的组合过程中，需要考虑动作的匹配，如果两个自动机存在可以匹配的动作，且这两个动作的使能条件可以同时满足时，这两个动作可以同步生成为一个内部动作；如果两个动作不匹配，那么这两个动作将会交替执行下去。两个自动机在组合过程中既可能存在同步互补动作，也可能存在交替执行动作。

4.2 PHCOIA的组合算法

PHCOIA组合算法，将M1,M2进行组合，M1=(Q1,Q01,A1,Σ1,X1,Xinit1,Fa1,F1,Enab1,E1,I1,P1,H1),M2=(Q2,Q02,A2,Σ2,X2,Xinit2,Fa2,F2,Enab2,E2,I2,P2,H2),输出为组合后的自动机S=(Q,Q0,A,Σ,X,Xinit,Fa,F,Enab,E,I,P,H)。下面给出PHCOIA组合算法的具体步骤：

2、从自动机M1和M2的初始状态进行状态组合，如果M1和M2的初始状态不能进行组合，则返回错误信息；否则标记Q01和Q02，自动机S的初始状态Q0为Q01和Q02的状态组合，将Q0添加到状态集合Q中，状态Q0内部的初始变量赋值Xinit等于Q01和Q02状态内变量的初始值，状态Q0内的赋值函数、流函数以及不变式约束分别为Q01和Q02上赋值函数的并集、流函数的并集和不变式约束的并集；将状态S1,S2,SPre分别置为Q01,Q02和Q0，跳转到步骤3；

3、如果M1和M2中的状态都被标记过，则H=(H1,H2)，组合完成程序返回；如果S1,S2都存在后继状态变迁，则跳转到步骤4；如果S1存在状态变迁而S2不存在，则跳转到步骤8；如果S1不存在状态变迁而S2存在，则跳转到步骤9；如果都不存在变迁，程序返回；

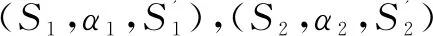
7、步骤7的内容与步骤6的内容相似，不再重复赘述；

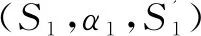
9、步骤9的内容与步骤8的内容相似，不再重复赘述。

4.3 PHCOIA的组合验证

PHCOIA的组合算法通过遍历自动机中的所有迁移来实现两个自动机的兼容性组合。利用该算法可以直接对两个PHCOIA进行组合相容性错误检测。如果在组合过程中，需要组合的两个状态内包含的变量有交集，或者在动作的组合过程中，当前自动机中的同步动作与目标自动机在保证动作先后序列的前提下无法找到与之匹配的动作或者两个同步动作不匹配，则判定出现相容性错误，给出错误提醒。

5 基于PHCOIA的应用实例

本节使用PHCOIA对飞行器的对接过程进行建模。在两个飞行器的对接过程中，后面追赶的飞行器称作追赶者飞行器(chaser),需要对接到的飞行器称为目标飞行器(target)，追赶者沿着半径为r1的轨道以角速度θ1运行。为了顺利地与目标飞行器完成对接，追赶者需要先在低轨道上改变自身的角度姿势，然后再逐渐上升到目标飞行器所在的高度进行对接。当上升到一定高度之后，追赶者将发送对接信号dock与目标飞行器进行对接。飞行器的每一次对接并不能保证完全的成功，存在一定的失败机率。如果对接失败，目标飞行器将会发送失败信号error，追赶者接收到信号后将会下降自身高度，重新调整角度，准备下一次的对接；如果对接成功，追赶者将会收到目标飞行器发送的对接成功信号success，并与目标飞行器以相同的角速度一同运行下去。

追赶者的PHCOIA如图1所示，目标飞行器的PHCOIA如图2所示。

图1 追赶者飞行器的PHCOIA

图2 目标飞行器的PHCOIA

两个飞行器的组合建模如图3所示。为了建模的简单呈现，所有的输入输出动作都组合成了内部动作。从组合后的PHCOIA中，可以很直观地看出对接过程中，各个系统内部的连续变化特性以及状态迁移上的概率不确定性，同时系统内部各个组件的交互行为也能够通过组件交互自动机很好地保存下来。

图3 组合后的PHCOIA

6 结束语

在COIA的基础上，针对CPS，提出了概率混成组件交互自动机的概念。PHCOIA不仅能够详细地描述组件之间的交互行为，还能够清楚地刻画出组件状态内的连续变化特性以及状态变迁上的概率选择性。可以利用PHCOIA对CPS中的各个组件进行准确建模。在给出PHCOIA的相关定义之后，还给出了其相应的组合算法，根据组合算法可以将表示各个组件的自动机进行组合，从而构建出一个完整的表示原系统的PHCOIA。在接下来的工作中，将着手在PHCOIA上开展形式化验证的研究，使其能够在PHCOIA上验证相关性质。