基于小波特征和支持向量机的非侵入式负荷识别

杜刃刃，杨 超*，王华勇

(1.贵州大学 电气工程学院，贵州 贵阳 550025；2.南瑞集团有限公司 国网电力科学研究院有限公司，江苏 南京 211106；3.国电南瑞科技股份有限公司，江苏 南京 211106)

非侵入式负荷监测技术(non-intrusive load monitoring，NILM)是由美国学者Hart在20世纪80年代提出的，即通过使用监测装置来测量家庭入口总线处的电压及其电流，建立家用电器负荷特征库，使用机器学习算法实现对家用负荷的非侵入式负荷识别[1]。传统的侵入式负荷监测技术，是在每个家用电器上安装传感器，实现对每个电器设备的电压和电流的采集，其优点是采集的数据准确度高，可以安全、稳定地监测家庭电器设备，但安装较困难、成本高、易于侵犯用户的个人隐私，推广难度较高[2]。而NILM与传统的侵入式负荷检测技术相比，具有成本低、易安装、能保护用户的隐私、易推广等优点[3-4]。

随着智能电网和泛在物联网的兴起，NILM成为国内外众多相关学者的研究热点。文献[5]采用模糊C均值聚类(fuzzy c-means,FCM)得到用电设备正常运行时电压和电流的稳态特征，再通过微分进化算法(differential evolution algorithm,DE)对用电设备进行分解，该方法对常阻抗和非常阻抗的用电设备大类分解效果比较好，但是分解用电设备类型不够精准。文献[6]使用小波设计和普鲁克分析来提取家用负荷的开关暂态特征，小波的能量系数作为特征值，采用半监督机器学习算法,以此进行负荷识别，具有较高的识别准确率，但是对于不同工作状态运行的家用负荷的识别准确率较低，以及该方法不适用多负荷的同时运行。文献[7]采用状态概率因子作为新特征，在低频采样条件下，采用Mean-Shift算法来构建家用负荷，在不同运行状态下的负荷特征库，通过将状态概率因子引入遗传算法的目标函数，从而提高寻优效率，以提高低功率负荷的识别准确率。该方法对于低功率负荷有较高的识别正确率，但是大功率负荷易影响小功率家用负荷，因此该方法对小功率负荷的识别准确率不佳。文献[8]使用采集的单个家用负荷电流负荷特征滤波器，对采集的家用负荷总电流进行频谱分析并进行赋值，得到对应的模板滤波器，但是使用快速傅里叶变换进行频谱分析时，会丢失时间局部化信息，不能定位电器开、关状态发生的时刻，并且有电流噪声的干扰，影响负荷识别的准确率。

针对以上出现的问题，本文提出了一种新的非侵入式负荷识别方法，对家用负荷进行负荷识别。首先，除采用有功功率和三次谐波电流幅值作为传统的基础特征外，还使用小波的能量系数作为新的特征，小波变换能够较好地定位家用负荷信号的波形特征，具有多分辨率的特点，保留信号时域和频域的局部特征；其次，是使用支持向量机算法(support vector machine, SVM)进行负荷识别；最后，用实测数据进行多场景实验，验证该方法在多场景下具有较高的识别准确率和良好的鲁棒性。

1 家用负荷特征分析

在低频稳态特征下，有功功率和无功功率是传统的基本特征，适用于家用负荷功率差别较大的情形，但大功率家用电器设备会掩盖小功率的家用电器设备，以致会影响家用负荷的识别准确率[9]。由文献[10]可知，低功率家用负荷设备的三次谐波电流幅值有较大的差异。因此，本文使用特征组1:有功功率、三次谐波电流幅值、无功功率;特征组2:有功功率、三次谐波电流幅值、小波的能量系数，两组特征进行负荷识别。

其中，有功功率和无功功率的公式如式(1)和(2)所示：

(1)

(2)

1.1 小波变换的能量系数特征提取

小波变换使用小波函数来分析非平稳信号，在NILM应用中，提取家用负荷信号中所包含的隐藏特征。离散的小波变换具有较好的时频特性和多分辨率的特点，因而可以更好地将信号分离出不同特性的分量。在基于小波变换的信号处理中，可以依据有用信号和噪声信号的展开系数的幅值，分离出信号的不同分量。因此，本文将变化的小波系数的能量值，通过数值变形计算，可用于家用负荷识别。

一维信号X(t)的二进制小波分解由式(3)表示：

X(t)=Aj+∑Dj。

(3)

式中：A为近似信号，表示为低频部分；D为细节信号，表示为高频部分。

一维信号X(t)与尺度函数V通过卷积运算可得到低频的近似系数cAj(l)。一维信号X(t)与小波函数W通过卷积运算可得到高频的细节系数cDj(l)[11]。其近似系数和细节系数可由式(4)表示：

(4)

计算小波系数的能量E由式(5)表示：

(5)

式中，l=1,2,…,N/2j-1，N是信号长度。

选择第j层的近似系数的能量和各层细节系数的能量作为负荷特征，构建小波的能量系数特征向量模型，由式(6)表示：

[EAj,ED1,ED2,…,EDj]。

(6)

使用离散小波变换，选取Daubenhies小波系数中的db5小波，分别对各家用负荷特征数据进行小波3层分解，使用公式(4)分别得到1个小波近似系数和3个细节系数，使用公式(5)提取近似系数的能量和各层细节系数的能量，作为家用负荷特征。其3种负荷的能量谱和5种负荷的能量谱如图1和图2所示。

利用小波变换分析高频家用负荷信号，可以提取出家用负荷开、关运行状态的高频暂态信号，暂态信号具有丰富的负荷特征信息，弥补了低频稳态信号表征负荷特征的不足。

由图1和图2可知，使用小波分析进行3层分解，提取近似系数的能量和细节系数的能量，可以展示出丰富的高频负荷信号的细节信息，特别是低功率家用负荷在细节系数的能量与其他负荷的差异，为我们进行含有低功率负荷的识别，打下了良好的基础。

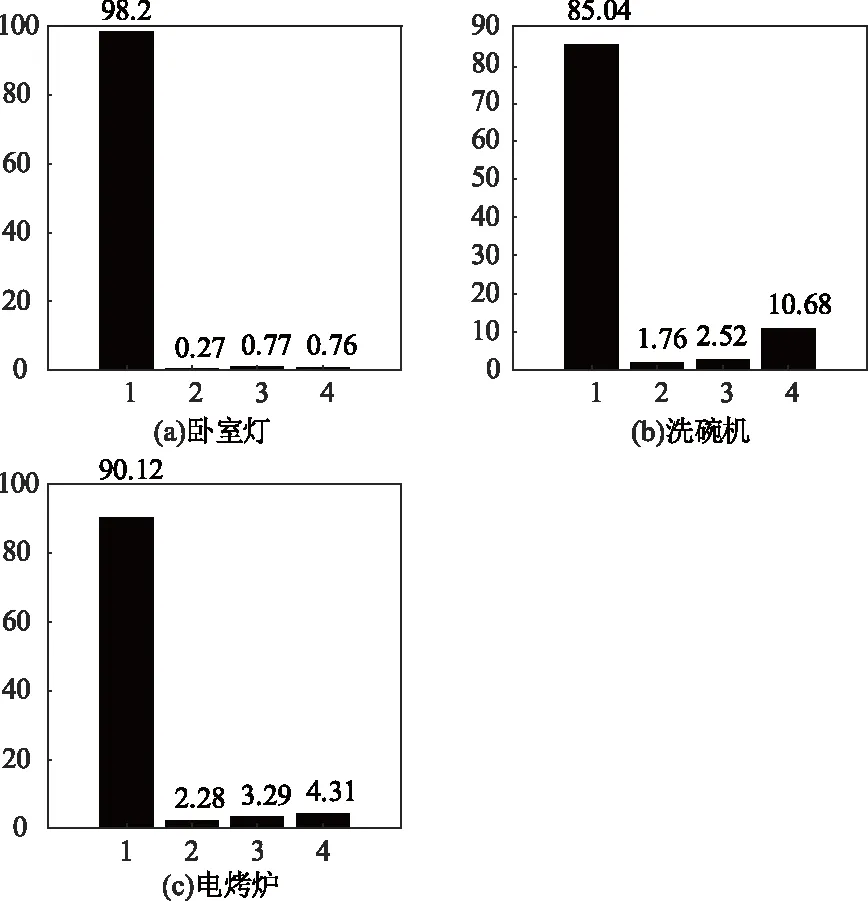
图1 3种负荷的能量谱

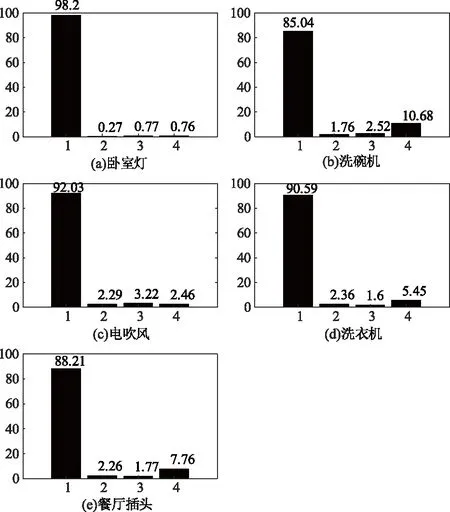
图2 5种负荷的能量谱

2 家用负荷特征数据的预处理

据大量的研究发现，在进行家用负荷数据采集时，会出现5%～10%的异常数据，主要为奇异值和缺失值[12]。异常数据会对负荷识别的结果产生影响，降低负荷识别的准确率。因此在进行负荷识别之前，有必要对采集的负荷数据进行预处理。

为了去除奇异值和噪声信号对NILM造成影响，采用小波变换对采集的信号进行去噪[13]。其小波去噪的流程如下：

1)选择一个小波基函数，对采集的家用负荷特征数据进行等间隔离散抽样，得到采集信号对应的离散采样点序列，然后基于离散的采样点序列进行N级小波分解，得到N级不同尺度的小波细节系数和一级小波近似系数；

2)对展开的各级小波细节系数，选择对应的阈值(硬阈值和软阈值)和阈值规则，以此进行阈值化处理，得到通过阈值处理后的各级离散小波细节系数；

3)对使用阈值处理后的各级离散小波细节系数和未处理的小波近似系数，进行N级小波反变换重构信号。

洗衣机在90 min内电流幅值的数据分别使用db2小波函数进行6级小波去噪和中值滤波去噪处理。其负荷特征电流幅值在去噪前后如图3所示：

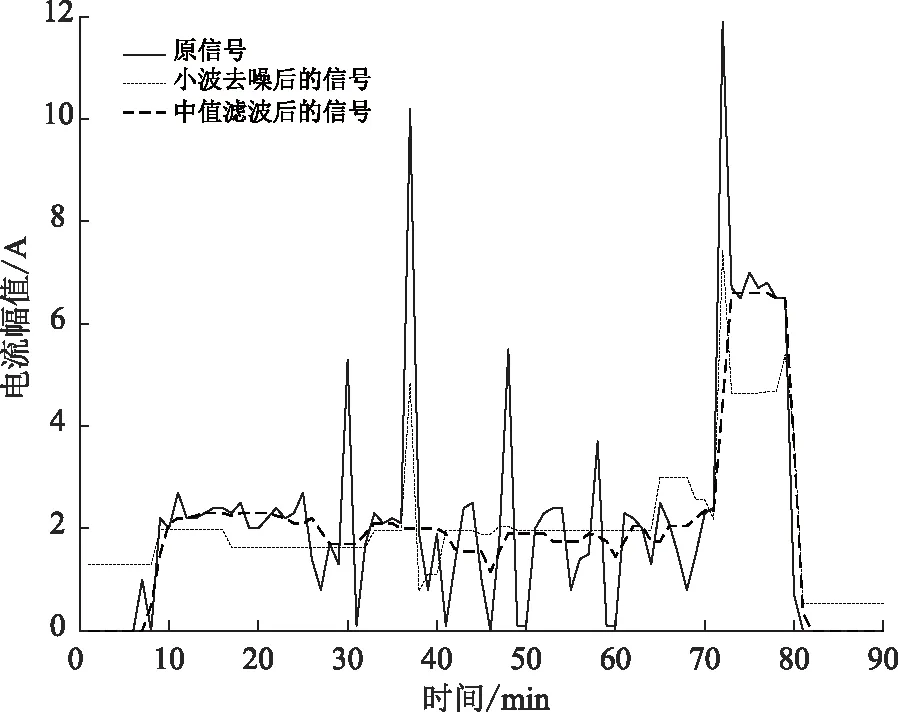
图3 洗衣机小波去噪前后电流幅值比较

信噪比SHR和均方误差RMSE是衡量洗衣机的负荷特征数据，进行小波去噪和中值滤波去噪效果的重要指标，如表1所示：

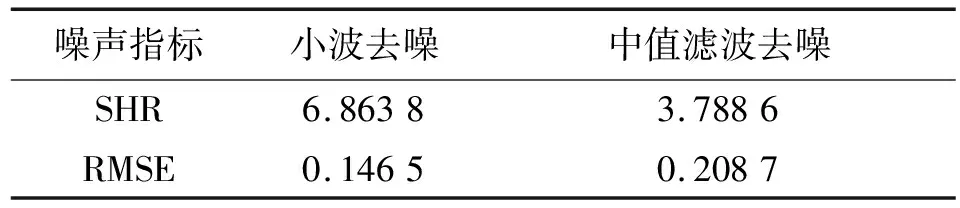
表1 去噪效果对比

由图3可知，采集的家用负荷原始信号在通过小波去噪后，剔除了异常的奇异值数据，使电流幅值波形变得比较平滑，提高了负荷识别的正确率。小波变换与快速傅里叶变换相比，可以保留信号的时域特征，适用于非平稳信号的分析，具有多分辨率的特点，能更好地满足信号地时频分析。

从图2和表1可知，使用小波去噪效果较为理想，其SHR和RMSE两个指标与中值滤波去噪相比，都有显著的提高。因此，本文使用小波去噪对两种特征组进行去噪。

3 NILM方法的原理与实现过程

3.1 支持向量机算法

支持向量机是基于数学统计理论提出的一种监督型机器学习算法。SVM在工程应用中常被用来解决分类和预测的问题，是数据挖掘中常用的方法[14]。SVM可分为二分类和多分类。本文采用多分类的支持向量机，对解决非线性的负荷数据，进行模式识别有着较大的优势。

设预处理后的负荷特征作为训练集T={(x1,y1),…,(xl,yl)}∈(R×Y)l，xi∈Rl,yi∈Y={1,2,…,M},i=1,2,…,l，其中第i个负荷特征为Ti∈Rd。对于多分类的支持向量机，由文献[14]可知，其目标函数如式(7)表示:

(7)

其中，C为惩罚因子，K(xi,xj)=(φ(xi)·φ(xj))为核函数，本文选取径向基核函数g。

在工程应用中，大多数家用负荷数据为非线性可分的，对于非线性不可分的情况，SVM算法选择一种适合的核函数和惩罚因子C，将预处理后的家用负荷矩阵经过压缩后使用核函数映射到更高维的空间，由此原来低维的负荷矩阵非线性不可分，映射到高维空间后变成负荷数据线性可分，解决了在原始低维空间线性不可分的负荷识别问题。SVM的决策函数基本形式由式(8)所示：

(8)

3.2 SVM算法在NILM中的实现

SVM算法具有较高的分类准确率，在进行训练集和测试集的归一化和小波去噪处理后，使用支持向量机对家用负荷进行识别的具体流程如图4所示。

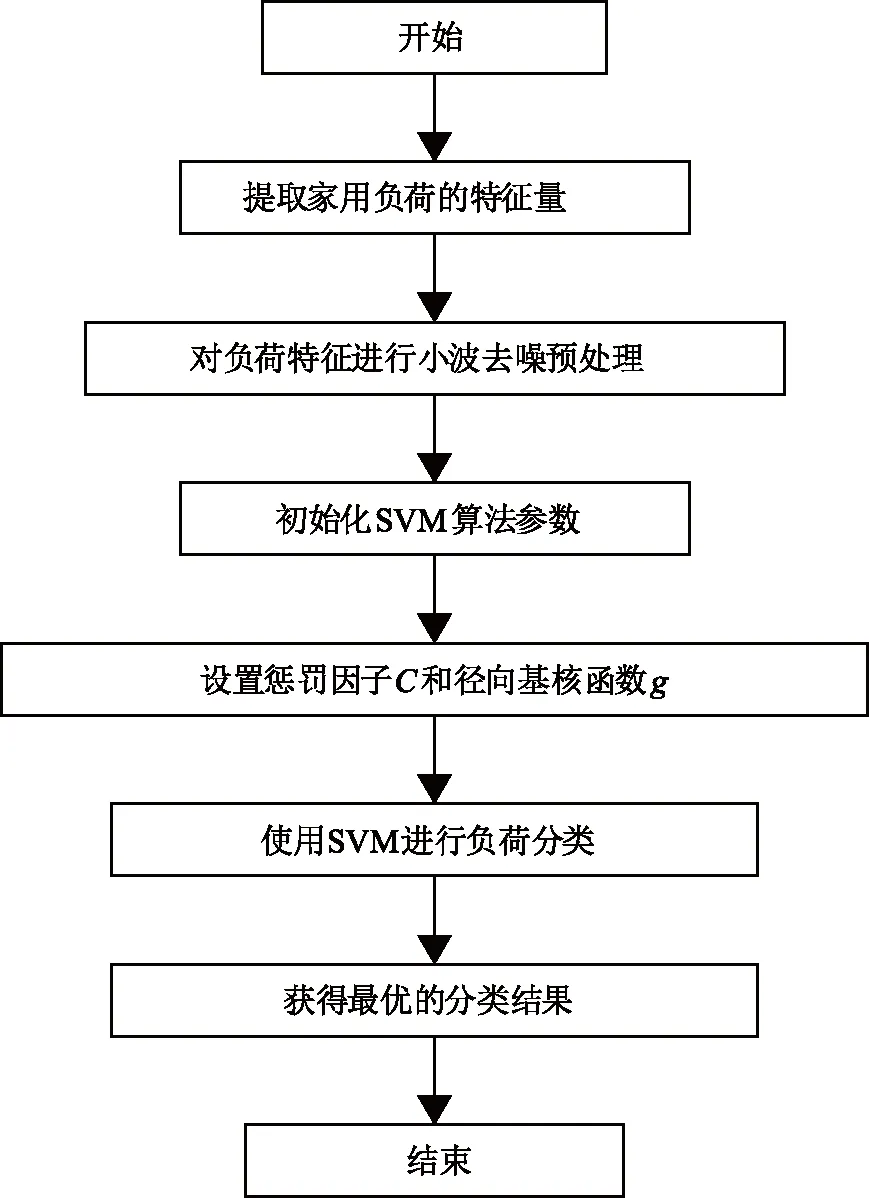
图4 SVM在NILM中的实现流程

SVM算法在NILM的实现流程如下所示：

1)提取家用负荷的特征量；

2)对采集的家用负荷数据特征进行预处理，主要是小波去噪和归一化；

3)对SVM算法进行参数初始化；

4)设置惩罚因子C的大小，选择径向基函数(radial basis function , RBF)g作为支持向量机的核函数；

5)采用支持向量机算法进行负荷分类；

6)最终获得最优的分类结果。

4 实验结果分析

本文使用SVM算法对国外公开数据集AMpds进行非侵入式负荷识别，利用MATLAB 2017b对负荷识别算法进行编辑运行。AMpds数据集每隔1 min采集数据一次，记录了21种家用负荷的电力数据，共持续监测730 d[15]。本文选取有功功率、三次谐波电流幅值和小波的能量系数作为负荷特征。为验证本方法在含有低功率负荷、多种场景下的适用性，本文使用3种和5种负荷的两种场景。

4.1 3种家用负荷场景

场景1选取AMpds数据集中3种家用负荷：卧室灯(84 W)、洗碗机(270 W)、电烤炉(646 W)进行实验，其中卧室灯属于低功率家用负荷。训练集选用2013-3-1～2013-3-7的家用负荷数据，测试集选用2013-3-15～2013-3-20的家庭负荷数据。

首先，选取家用负荷数据的训练集和测试集，进行负荷特征提取；然后，分别对训练集和测试集提取的特征进行预处理操作，主要是进行小波去噪，以此减少电力数据中奇异值对负荷识别的影响；选取数字1、2、3作为训练集中相应负荷种类的标签，选择径向基函数(RBF)g作为SVM的核函数，设置SVM算法的参数C=100，g=100，使用训练集生成支持向量机的训练模型；最后，使用测试集在SVM的训练模型上进行家用负荷分类。由SVM进行负荷分类后，3种家用负荷识别准确率如表2所示。

由表2可知：使用传统的有功功率、三次谐波电流幅值和无功功率组成的特征组1，识别的准确率较低；在传统的有功功率和三次谐波电流幅值的基础上，引入小波的能量系数作为新的特征，组成特征组2，使用SVM算法进行分类，有较高的识别准确率。因此，在对提取的负荷特征进行小波去噪后，使用SVM算法对家用负荷进行分类，含有小波的能量系数的特征组2与传统的特征组1相比，识别准确率提高了10.9%，尤其是低功率负荷的识别有着显著的提升。

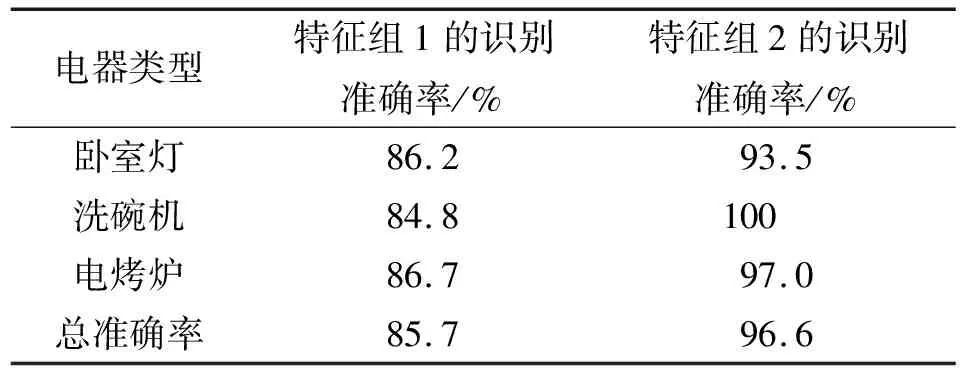
表2 3种家用负荷识别准确率

4.2 5种家用负荷场景

场景2选取国外公共数据及AMpds中5种家用负荷：卧室灯(84 W)、洗碗机(270 W)、电吹风(1500 W)、洗衣机(720 W)、餐厅插头(55 W)进行实验，其中卧室灯和餐厅插头属于低功率家用负荷。训练集选用2013-9-11～2013-9-18的家用负荷数据，测试集选用2013-9-25～2013-9-30的家庭负荷数据。

场景2选取的训练集和测试集的处理方法和3种家用负荷场景相同；然后分别对预处理后的特征量进行小波去噪；使用数字1、2、3、4、5作为去噪后的训练集中相应负荷种类的标签；选择RBF核函数作为支持向量机的核函数，设置SVM算法的参数C=100 ,g=100；最后使用SVM进行负荷识别，其5种家用负荷的识别准确率由表3所示：

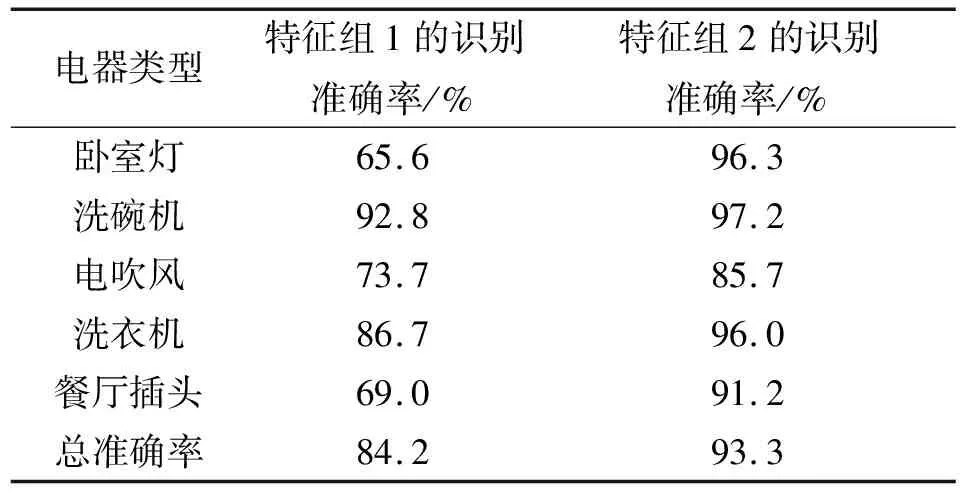
表3 5种家用负荷识别准确率

由表3可知，随着负荷种类的增多，使用两种特征组的负荷识别准确率都稍微降低。使用传统的有功功率、三次谐波电流幅值和无功功率的特征组1，进行负荷识别，对低功率的负荷识别准确率不理想。在引入小波的能量系数作为新特征后，使用SVM对特征组2进行负荷识别，与特征组1相比，识别准确率有着较大幅度的增加。特别是对低功率负荷的识别，比使用特征组1的负荷识别准确率显著增加。因此，引入新特征小波的能量系数，能够提高负荷识别的准确率。

5 结论

针对低功率家用负荷识别准确率低的问题，本文引入小波的能量系数作为新特征，来提高负荷识别的准确率。使用小波变换，对采集的家用负荷数据进行时频分析，与快速傅里叶变换相比，可以同时表征低频和高频分量，保存时域的有效负荷信息。本文选用的小波的能量系数可以表征负荷的有效信息，同时使用小波去噪进行去除奇异值，可以有效地降低噪声的影响。实验表明：本文使用的小波的能量系数新特征，对低功率负荷的识别准确率有着显著的提高，在多种场景下有着较高的识别准确率和良好的鲁棒性。