考虑收缩的爆炒热/质传递过程模拟与验证

谢 乐，邓 力，李静鹏,2，曾雪峰，闫 勇，石 宇，苏婕妤

考虑收缩的爆炒热/质传递过程模拟与验证

谢 乐1，邓 力1※，李静鹏1,2，曾雪峰1，闫 勇3，石 宇1，苏婕妤1

（1. 贵州大学酿酒与食品工程学院，贵阳 550025；2. 江南大学食品学院，无锡 214122；3. 贵州汉食精工科技有限公司，贵阳 550025）

为研究爆炒中食品多孔介质热/质传递机制及烹饪成熟和品质变化规律，考虑收缩-水分损失关系，基于多孔介质理论，结合傅里叶定律、牛顿冷却定律和达西定律，构建了爆炒中有蒸发、考虑收缩的食品含湿非饱和多孔介质热/质传递数学模型，开展了爆炒数值模拟。考虑收缩后模拟值与实测温度历史（Least Summation of the squared Temperature Difference for overall target，LSTD=4.40 ℃）、平均含水率（LSTD=1.42%）和体积收缩率（LSTD=1.05%）吻合更为良好。模拟分析了爆炒热/质传递对颗粒表面蒸发、收缩、内部压力、水分和温度分布的影响机理及火候控制手段的作用，结果表明：爆炒强对流传热使颗粒蒸发剧烈造成水分损失；收缩主要由水分损失引起，可以增大传热效率并影响颗粒内部压力变化，由成熟值理论研判，蒸发收缩对烹饪成熟起到促进作用，并有利于提高烹饪品质，是爆炒技术优势的一部分；火候控制手段通过改变颗粒特征尺寸、能量传递速率和流体-颗粒的换热时间/接触面积对颗粒成熟时间和含水率等烹饪品质产生极显著（<0.01）影响。

数值模拟；模型；水分；爆炒烹饪；收缩；热/质传递

0 引 言

中式烹饪是中国十多亿国民的主要饮食形式，2019年全国餐饮收入达到了46 721亿元。有必要对中式烹饪开展系统、深入地研究，把握烹饪过程传热与品质变化的内在原理，以推进烹饪科学的进步及烹饪的自动化、标准化。最具特色、应用最广泛的中式烹调方法是以油脂为主要传热介质的爆炒，具有加热功率高、蒸发强烈、搅拌剧烈和加热时间短的特点，其过程复杂、优化控制难。传热对烹饪品质具有决定性影响[1-2]，而食品颗粒在爆炒过程中处于非稳态传热状态，内部温度随时间和空间位置变化，测量难度极大[1]。已有近10种采集液体-颗粒传热中颗粒内部温度历史的方法[3]，其中热电偶法[4]和数值模拟法[5]应用较多。而数值模拟法更适用于爆炒烹饪研究，能获取烹饪中食品各组分、物理场的全局变化，具有成本低、效率高、受试验条件限制较小等优点，是总体掌握爆炒中食品颗粒传热过程的唯一手段。

食品热处理数值模拟常忽略原料收缩。这是由于除了干燥外的西式食品烹饪热处理过程常为煎制[6]、深层油炸[7]、烘烤[8]等，烹饪过程温和、时间较长。忽略收缩可以降低数学模型的复杂性和计算成本，但也常造成计算误差[9]。而畜肉作为典型烹饪对象，在爆炒中短时间内出现肉眼可见的快速收缩。收缩是烹饪研究中无法回避的现象，其发生机理和特征、对烹饪传热和品质优化的影响均应进行深入探索[10]。收缩不只改变了原料尺寸，还进一步影响了诸如饱和度、孔隙率等一系列物性参数以及对流换热系数和对流传质系数[11]。后两者对烹饪成熟和品质优化影响很大[1]。并且，食品热处理中的收缩现象耦合了热量和质量传递，部分还涉及到动量传递过程[12]，与传递过程之间的相互作用非常复杂。

目前，在食品热处理研究领域有2种方式描述收缩现象。一种以经验公式直接将烹饪中面积或体积收缩与含水率、温度和加热时间相联系，Costa等[13]以温度-厚度经验公式对油炸法式薯条体积收缩进行了数学描述，认为水分损失是土豆体积收缩的主要影响因素，此类方法的预测值与实测值拟合度较高，但通常仅限于收缩模型构建，未考虑热/质传递过程。由于收缩现象主要与原料的失水有关[14]，建模中忽略热/质传递过程，使得模型的应用仅限于特定性质的原料和特定热处理条件，造成其适用范围受到限制。显然，这种方式不适于研究原料极其多样、热处理方式复杂的中式烹饪收缩现象。

另一种方式以数学物理方程模型对收缩进行建模，Li等[15]认为原料收缩量在烹饪加热过程呈非线性，收缩现象由应力造成，而收缩应力由水分损失引起，针对花竹虾水浴加热过程，将其视作各向同性黏弹性材料，构建了有收缩现象的热/质传递过程数学模型；此类考虑收缩现象的热/质传递过程数学模型，结合了多孔介质理论，能解释食品水分损失造成收缩的机理。但以上热处理过程相较中式爆炒都明显温和平缓，不能直接应用于爆炒过程研究。

本文在前期研究基础上，构建了有收缩的爆炒热/质传递过程数学模型，数值模拟爆炒中的各项变化；并结合成熟值理论，探究了爆炒烹饪中火候控制手段如原料切割技术、预热油温和搅拌操作对食品颗粒成熟规律和品质的影响，旨在为中式烹饪的品质优化、过程控制提供原理和方法支持。

1 材料、理论、数学模型与方法

1.1 样本材料

食用油、圆柱形取样器和保鲜膜，市售；猪里脊肉，购于贵州省贵阳市花溪区合力超市。

1.2 仪器和设备

超级恒温油浴槽DF-101T，含可调速磁力搅拌器（邦西仪器科技（上海）有限公司）；热电偶定位器，3D打印制作[16]（自研，贵州大学）；烹饪传热学及动力学实时采集系统[17]（自研，贵州大学）；戴尔T7810工作站E5-2603 v3/8GB/500GB/NV K620（戴尔（中国）有限公司）；LX-5相机（佳能（中国）有限公司）；MB35快速水分测定仪（奥豪斯国际贸易有限公司）。

1.3 烹饪成熟动力学原理

邓力[2]基于值动力学模型提出了成熟值理论，以动力学角度将传热温度变化与烹饪品质联系起来，可定量描述烹饪成熟与品质。故引入成熟值理论以探究爆炒中原料成熟、烹饪品质的内在规律。

成熟值（Maturity value，）：由特定人群感官评价判定某一特定品质的成熟程度相对参考温度的等效加热时间[18]，表达式如下：

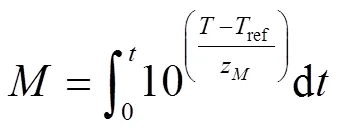
式中为颗粒温度，℃；ref为参考温度，℃；z为基于感官评价的烹饪成熟品质因子值，℃，可以反映感官评价时品质因子对烹饪温度变化的敏感程度；为烹饪热处理时间，min。其中，感官评价过程需10名感官评价人员通过多个成熟品质因子判断标准，使用差别检验法挑选不同烹饪条件下每种品质因子刚好成熟的样品。

终点成熟值（Termination maturity value，M）：代表食品在烹饪过程中食品达到成熟时间点的成熟值，动力学表达式为

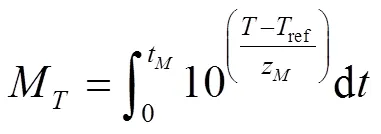
式中t为烹饪热处理最终时间，min。

文献[18]表明，M及其z值可以通过特定的感官评价方法和统计学分析计算测得，并测得猪里脊肉z值为10 ℃。

1.4 数学模型

前期研究中，邓力[1]对中式烹饪的液体-颗粒建立了热/质传递的多相多孔介质模型，对其最基本特征进行了总结；崔俊[19]构建了适用于爆炒烹饪有表面蒸发的多孔介质热/质传递数学模型，初步解决了有蒸发的中式烹饪液体-颗粒热处理数值模拟问题；余冰妍[20]在此基础上完善和验证了数学模型，实测了爆炒过程中对流传质系数（h）以及猪里脊肉的固有渗透率。虽然以上均以猪里脊肉为固态颗粒的模型较为完备，验证中也体现了较高准确度，但都忽略了收缩。可以推断这些模型中的一些条件和参数（如水分蒸发量、对流-颗粒对流换热系数（fp）、孔隙率等）偏离了真值，抵消了收缩所产生的影响。这些偏差会影响模型在不同条件下的适用性和准确性。

爆炒过程的特征是开放容器内被搅拌液体-颗粒的热/质传递过程和品质变化过程。其传热过程包括了热源对容器外壁辐射和对流、外壁-内壁的传导、油对容器内壁的对流、油与颗粒表面的对流、颗粒内部传导和颗粒表面水分蒸发6个传热过程与相变过程，各个传热过程均属非稳态，相较于油炸、干燥等食品工业常用热处理更为激烈、复杂，如图1。传热造成的内部温度梯度、表面蒸发造成的水分浓度梯度与压力梯度，为内部空气和水分向表面扩散和对流提供了动力，造成水分损失及收缩。传质过程包括了颗粒内空气和水分向边界对流与扩散、颗粒表面空气扩散和水分蒸发扩散，由于爆炒表面向外剧烈蒸发，颗粒成熟极快，油脂渗入极少，故研究中忽略油脂向颗粒内的传递。

图1 爆炒烹饪中液体-颗粒热/质传递及收缩过程

在中式烹饪中，绝大多数烹饪固体原料都可被视作含湿非饱和多孔介质，而收缩将改变诸如孔隙率、流体饱和度等受体积影响的多孔介质参数[21]；本研究参考Li等[15]将猪里脊肉视作各向同性的含湿非饱和多孔介质颗粒，缩小研究范围到油与单一颗粒。根据热量、质量及收缩间的耦合关系，建立了有蒸发、收缩的爆炒热/质传递过程数学模型。其中，能量控制方程由傅里叶定律、牛顿冷却定律等描述，见式（3）至式（6）；质量控制方程由菲克定律等描述，见式（7）至式（11）；动量控制方程采用达西定律描述颗粒内部流体流动，见式（12）；蒸发数学描述见式（17）至式（19）；收缩及边界移动由收缩体积-水分损失关系进行描述见，见式（23）至式（28）。

提出以下假设：油脂向颗粒内部的传递忽略不计；水分蒸发仅发生在颗粒表面，忽略表面壳层的形成；颗粒收缩现象为均匀收缩；颗粒均质为各向同性，颗粒内流体相连续；颗粒内部无热源、无化学反应、传热过程只考虑对流传热和热传导。

1.4.1 能量控制方程

在爆炒烹饪过程中，食品多孔介质的孔隙空间常被多种互不相溶的流体占据，存在多相系统，固相有食品颗粒，流体相有水、水蒸汽和空气。多孔介质传热过程的能量控制方程如下：

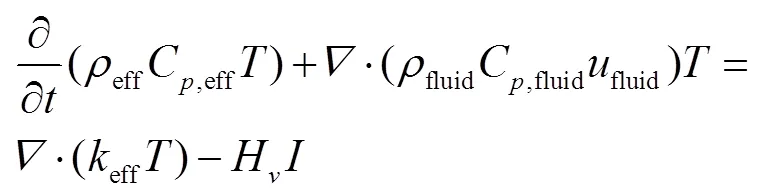
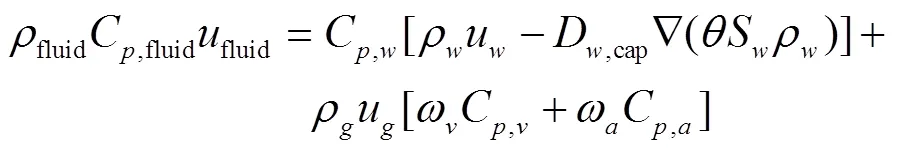
式中，为、、、分别代表固体骨架、水、空气、水蒸汽和空气水蒸汽混合气体；为孔隙率；ρ为相的密度，kg/m3、C,为相的比热容，J/(kg·K）；S为相的饱和度，无量纲；ω为相的质量分数，无量纲；X为相的摩尔分数，无量纲；k为相的导热系数，W/(m·K）；u为相在孔隙中的流速，m/s；Dcap为水的毛细管扩散系数，m2/s；。

1.4.2 质量控制方程

1）水分传质控制方程

式中从左至右各项式分别表示颗粒质量变化率、对流损失流量、扩散损失流量（菲克定律）和蒸发损失流量。

水的通量（n）可表示为：

式中n为水的通量，kg/(m2·s）；in,w为水的固有渗透率，m2；r,w为水的相对渗透率，无量纲；为气体总压力，Pa；cap为毛细管压力，Pa；μ为水的动力黏度，Pa·s。

2）混合气体传质控制方程

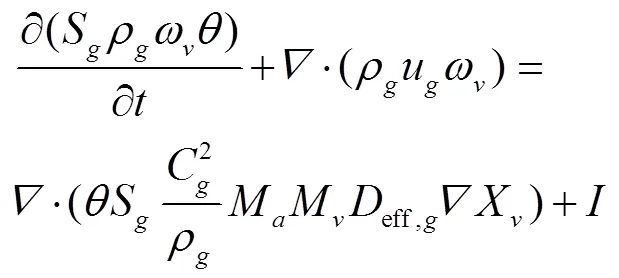
式中从左至右各项式分别表示非稳态项、对流项、扩散项和蒸发项。C为混合气体摩尔浓度，mol/m3；M为相的蒸汽摩尔质量，kg/mol；eff,g为混合气体有效扩散系数，m2/s；。

混合气体的通量以蒸汽的通量（n）进行描述，如下式：

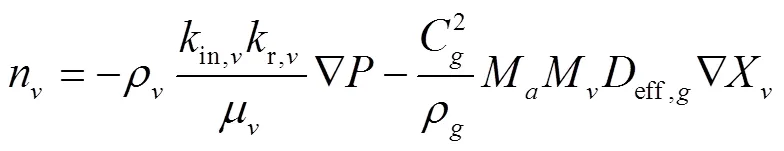
式中n为混合气体中蒸汽的通量，kg/(m2·s）；in,v为蒸汽固有渗透率，m2；r,v为蒸汽相对渗透率，无量纲；μ为水蒸气的动力黏度，Pa·s。

在混合气体中，可将蒸发产生的蒸汽作为混合气体中的质量源，蒸汽质量控制方程如下：

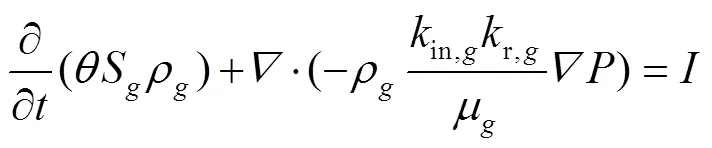
式中in,g为气体固有渗透率，m2；r,g为气体相对渗透率，无量纲；μ为气体的动力黏度，Pa·s。

1.4.3 动量控制方程

采用达西定律描述各相的流动，即：

式中描述空气、水和水蒸气等流体相流动时，分别为、、；in,,j为相的固有渗透率，m2；r,,j为相的相对渗透率；μ为相的动力黏度，Pa·s。

1.4.4 边界条件

1）能量传递边界条件

考虑了表面蒸发后，颗粒对流换热吸收的热量等于流体相提供的热量、表面水分蒸发失去能量和颗粒内热传递能量之和，边界条件为

式中从左至右各项式分别表示边界导热热流密度、边界流体流动热流密度、边界对流热流密度、表面蒸发热流密度，W/m2；fp为液体-颗粒对流换热系数，W/(m2·K），参照文献[22]，取215 W/(m2·K）；surf为颗粒表面温度，℃；amb加热介质温度，℃；为水的蒸发焓，J/(kg·mol）；sat为饱和蒸汽压，Pa；amb为环境压力，Pa；K是由刘易斯关系式求得的对流传质系数[23]，(kg·mol）/(s·m2·Pa），计算式如下：

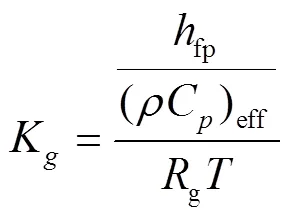
式中R为8 314.34(Pa·m3）/(kg·mol·K），气体常数。

2）质量传递边界条件

烹饪过程中，原料表面水分蒸发量等于水分扩散量，水分和蒸汽传质的边界条件为

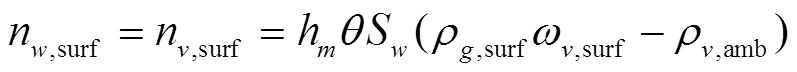
式中nsurf为颗粒表面水的通量，kg/(m2·s）；n,surf为颗粒表面蒸汽通量，kg/(m2·s）；h为对流传质系数，m/s，参照文献[24]取0.028 m/s；ρ,surf为颗粒表面气体密度，kg/m3；ρ,amb为环境蒸汽密度，kg/m3；ω,surf为颗粒表面蒸汽质量分数，无量纲。

3）动量传递边界条件

颗粒表面的总压力在爆炒过程中保持不变，边界条件为

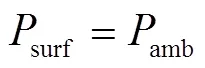
式中surf为颗粒表面压力，Pa。

1.4.5 蒸发数学描述

爆炒中相变过程是气相与液相间的非线性瞬态热/质传递过程。通过平衡与非平衡方程计算水分蒸发速率。Ratti等[25]假设水蒸气与液体水达到平衡，使用湿度等温线描述特定含水率和温度下的平衡蒸汽压：

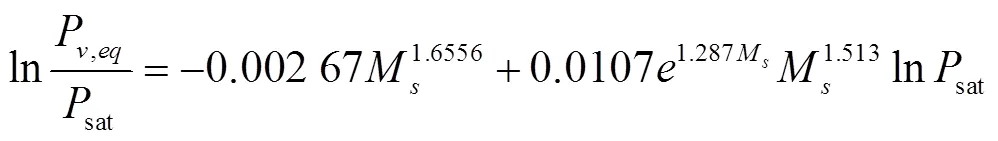
式中P为平衡蒸汽压，Pa；M为干基水分含量，无量纲，由下式计算：

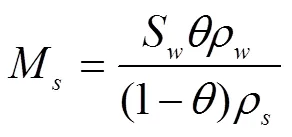
参照Le等[26]非平衡方程计算方法，构建多孔介质水分相变数学描述：

式中ρ为平衡蒸汽密度，kg/m3；为蒸发速率常数，1/s。

1.4.6 引入收缩过程

1）体积收缩数学描述

烹饪过程中肉类的收缩主要由水分损失造成，Briskey等[27]发现牛肉在40 ℃到50 ℃时持水能力会大幅下降，当内部温度高于50 ℃后，会出现滴汁现象，而当温度上升至70 ℃后收缩更加明显[10]。参照Feyissa等[28]的方法以收缩体积-水分损失关系对爆炒中原料收缩进行数学描述：

式中V为时刻原料肉的体积，m3；0为样品的初始体积，m3；V为样品在烹饪过程时刻的失水体积，m3；为孔隙生成系数，取值范围0到1，无量纲。其中，描述烹饪过程中生成的孔隙所造成的影响，当=1时代表无孔隙生成，水分损失体积与收缩体积相当；当=0时代表大量孔隙生成，但此时孔隙中流失的水分完全被空气代替，不发生收缩。猪里脊肉的可取0.8[28]。

依据假设，多孔介质为各项同性，其收缩体积变化可写作式（21）：

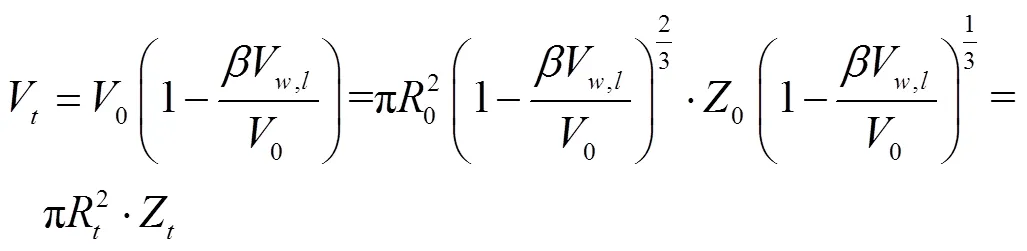
式中R为时刻原料肉圆柱的半径，m；Z为时刻原料肉圆柱的高，m；0和0分别代表初始半径和初始高，m；其中，R、Z和V由式（22）至式（24）计算：

式中0为初始湿基含水率，kg/kg；av为平均湿基含水率，kg/kg；ρ为水的密度，kg/m3；0原料肉的初始密度，kg/m3。

水分损失速率可通过水分损失体积对时间求导得到，如式（25）。通过热/质传递过程控制方程求解得到平均干基含水率av，使用式（26）转换为平均湿基水分含量av。

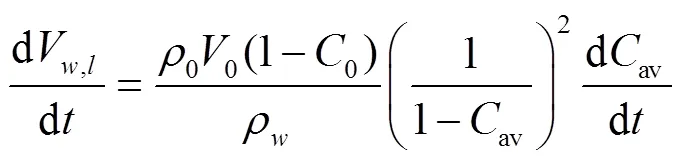
式中av由下式求得：

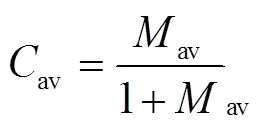
式中av为平均干基含水率，无量纲。

2）边界移动速度方程

通过式（22）和式（23）对时间求导，求得半径方向边界移动速度v和高度方向边界移动速度v。

1.4.7 物性参数

物性参数，见表1。

1.4.8 几何模型的构建及网格划分

选取圆柱中心截面1/2进行二维轴对称模型建模，尺寸为0.65 cm×1.00 cm（半径×高），边界条件只加载于暴露在外的3个边界上，余下边界为绝热面。经网格无关性验证后，选择计算成本较低的“细化”单元大小，网格划分后共有网格三角形628个，网格顶点347个。为降低计算成本，使模型求解计算更易收敛，通过COMSOL Multiphysics 4.3b（COMSOL，Inc.，Burlington，Mass）后处理的二维旋转（Revolution 2D）功能处理数据集，如图2。

表1 计算中物性参数

注：S为水的饱和度，为颗粒温度，℃。

Note: Sis water saturation,is particle temperature, ℃.

图2 数据集二维旋转和网格划分示意图

1.4.9 数值模拟

采用COMSOL Multiphysics 4.3b（COMSOL，Inc.，Burlington，Mass）求解多孔介质热质/传递过程和收缩过程，通过MATLAB R2014b（迈斯沃克软件（北京）有限公司）编程计算成熟值和终点成熟值。数值模拟步骤分为3步：1）使用“广义型偏微分方程”模块加载能量控制方程式（3）至式（6）、质量控制方程式（7）至式（11）、蒸发数学描述式（19）、收缩数学模型式（20）到式（26），使用“达西定律”模块加载动量控制方程式（12），在“动网格（ALE）”模块中设置几何网格为“自由变形”并加载边界移动速度方程式（27）和式（28）中v、v指定方向边界和方向边界网格位移速度，同时对称面边界设置为“零法向网格速度”；2）研究步骤中开启“自动重新划分网格”，以“网格质量”作为重新划分条件，使用全耦合MUMPS直接求解器求解所有模块，得到温度、压力、含水率和水分蒸发量，在求得含水率基础上计算ALE模块，得到边界移动速度并重新划分网格；3）通过MATLAB R2014b（迈斯沃克软件（北京）有限公司）使用求解得到温度数据编程计算成熟值和终点成熟值。

模型验证试验数值模拟总时长为240 s，模型模拟应用数值模拟总时长为180 s，经时间步长无关性验证，为与烹饪传热学及动力学实时采集系统[17]的1 s采集时间间隔一致，数值模拟步长选择1 s。模拟应用包括：探究爆炒过程颗粒的各项变化如，表面蒸发速率、体积收缩率、内部压力、含水率、温度等变化规律和机制；结合成熟值理论，探究火候控制对颗粒烹饪成熟和品质的影响。具体流程如图3。

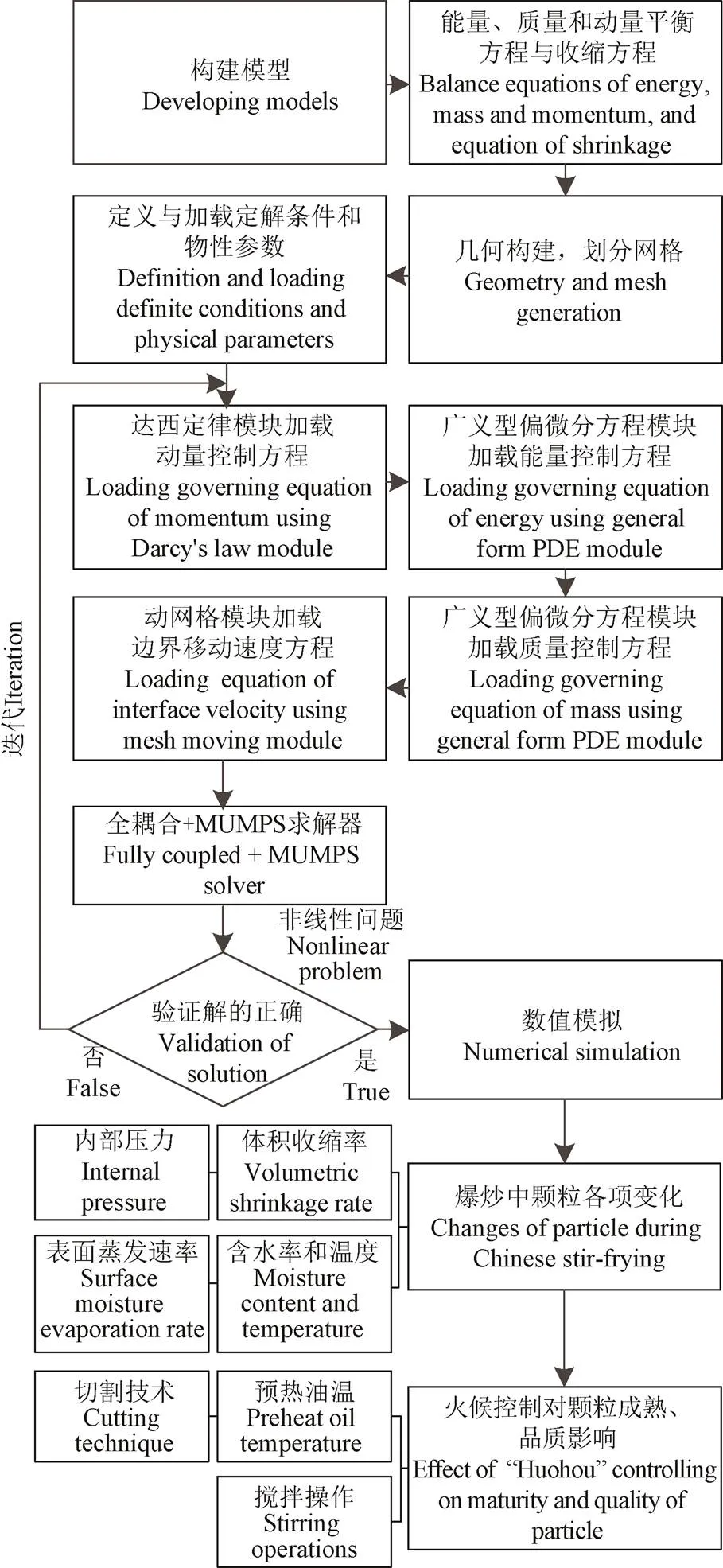
图3 爆炒热/质传递过程数值模拟流程图

1.5 试验方法

1.5.1 样品制备

使用0.65 cm×5.00 cm（半径×高）圆柱取样器，对4 h预冻于-10 ℃的猪里脊肉进行切割取样，取样方向平行肌肉纤维方向，切割获得0.65 cm×1.00 cm（半径×高）肉柱。

1.5.2 模型验证的统计学指标

1）样品准备

试验前，将已制备样品解冻至10 ℃。1次试验需至少准备来自同一猪里脊肉块的15根肉柱样本；2）中心温度历史测定使用定位器将热电偶置于样品肉柱几何中心位置，放入超级恒温油浴槽内油浴加热，温度设定120 ℃，转速2档，使用烹饪传热学及动力学实时采集系统[17]（图 4）对样品升温过程进行实时温度采集。以60 s间隔依次取出3根肉柱进行平均含水率与体积收缩率测量，直到240 s将连有热电偶的余下肉柱取出，停止采集，平行3次试验。每个样品取出后使用保鲜膜密封包装，冷却至室温备用；

3）含水率测定

使用快速水分测定仪测定样品的含水率，平行3次测量；

4）体积收缩率测定

参考Barbera等[33]的图像分析方法测量体积收缩率V。对肉柱进行三视图相机拍摄，借助图像处理软件分析测量每个样品圆柱的底面积与高度，计算V。

5）验证计算式

使用最小温度目标总体差平方法（LSTD）和相关系数方法[34]对试验值与数学模型模拟值进行计算。当LSTD值较小时，则认为两组曲线数值相似度高，即验证模拟值的准确性。

图4 爆炒模拟试验装置

2 结果与分析

2.1 模型验证

设定的数学模型定解条件和物性参数与试验条件、猪里脊肉物性参数一致。数值模拟爆炒过程颗粒中心温度历史、平均含水率和体积收缩率，通过模拟值与试验值对比的方法，验证模型的可靠性。

2.1.1 中心温度历史

考虑收缩的模型模拟温度值与试验值存在很小差异（LSTD=4.40 ℃，=0.999 7）。由图5a可得在约90 s时考虑收缩的模拟值略低于试验值，主要原因：加热后期肉柱表面剧烈蒸发使其在加热介质中运动以及收缩的不均匀性，使热电偶偏离几何中心位置，90 s后试验温度曲线偏高；为降低计算成本，模拟中fp设为恒定值，但在实际传热后期样品表面蒸发减弱导致fp减小，使得模拟温度出现误差。若模型不考虑收缩（图5a），该模拟值与试验值差异明显（LSTD=15.69 ℃，=0.997 5），在约40 ℃时与试验值偏离，符合Briskey等[27]报道，肉在40 ℃时持水能力开始下降出现收缩。模型考虑收缩后，LSTD值减小了72.0%，模拟值更符合试验值，吻合程度更好，相关性更高。显然，考虑收缩的爆炒过程热/质传递模型更为全面，鲁棒性更好。

2.1.2 平均含水率

图5b中爆炒过程原料平均含水率模拟值（LSTD=1.26%，=0.992 2）与试验值基本吻合。含水率在40 s至80 s出现了骤降，这是由于强烈的表面蒸发造成内外水分浓度差，使内部水分向外扩散和对流；收缩使体积减小，水分运输路径缩短更易损失。80 s后含水率下降趋势放缓。其原因可能是收缩使孔隙率减小造成，根据Kozeny-Carman方程，孔隙率（）与相对渗透率呈正相关[35]，孔隙率减小使内部水分相对渗透率（r,w）一并减小，使水分损失速率放缓。若不考虑收缩，模拟值在约40 s时与试验值发生明显偏离（LSTD=4.41%，=0.955 1）（图 5b），侧面反映了收缩对全程的水分传质效率的提高。

2.1.3 体积收缩率

食品原料常具有弹性，其收缩常与弹性体积变化、内部组分向外迁移造成的体积变化和由此产生的内外压力差有关。从图5c可得，爆炒中原料的体积收缩率模拟值（LSTD=1.05%，=0.998 8）与试验值基本吻合，体积收缩率呈非线性。在烹饪热处理过程中，固相的持水能力持续下降[27]，大量水分从固相多孔结构中迁出造成水分损失导致收缩[12]。模拟值略小于试验值是由于为降低模型复杂性和计算成本，本研究以收缩体积-水分损失关系对收缩进行描述，忽略了收缩过程中的应力作用，带来了计算误差。

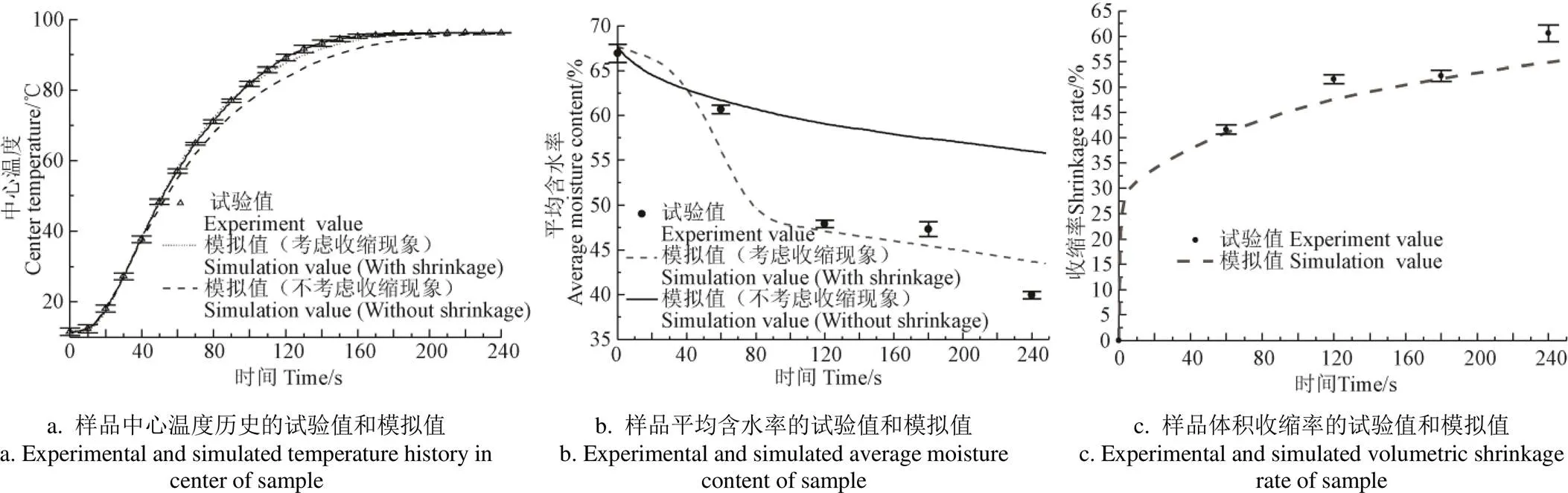
图5 验证试验结果

2.2 爆炒过程的各项变化

2.2.1 前期表面蒸发速率、体积收缩率和压力

图6a展示了爆炒前期6 s内颗粒表面水分蒸发速率、体积收缩率和半径方向距中心不同位置压力（表压）模拟值。如图6a所示在1 s前，表面蒸发速率和体积收缩率迅速上升，内部压力骤降为负压且距中心0.5 mm压力先于中心压力达到最小值。这是由于爆炒剧烈的对流传热带来的大量能量使表面水分迅速蒸发，引起的水分损失使体积收缩率增大，所造成的水分浓度梯度使内部水分迅速向外边界扩散和对流；水分向外迁移、内部空气排出使内部压力骤降。Chemkhi等[36]对陶器干燥过程的数值模拟中也出现了内部负压的情况。但因爆炒过程的剧烈性，负压出现时刻将更早、持续时间更短。约2 s后中心压力和浅层压力转为正压，压差由415 Pa变为12 Pa，中心压力略大于浅层压力。这是由于表面蒸发速率迅速上升后，水分损失及体积收缩率增大所产生的对内压力引起。因此，在爆炒前期颗粒表面水分蒸发速率增大将提高水分损失及体积收缩率；前期颗粒内部压力受体积收缩率的影响。

2.2.2 水分损失与体积收缩率

图6b展示了爆炒中原料颗粒内部水分空间分布随时间变化的情况。图中轴为含水率，轴为时间，轴为半径方向距中心点的距离。轴的颜色越深则代表内部含水率越低。图6b中，中心到边界距离随着传热的进行不断缩短，展示了颗粒的收缩过程。从图6b中的含水率等高线可以看出，内部水分浓度梯度在40至80 s时间段间出现了大幅度减少，水分传递过程加强，水分损失加剧，物料体积开始大幅减小。在120 s后，表面含水率急剧下降，表面含水率越低边界距中心点的距离越短，这是由于水分损失及收缩造成的压力驱动内部水分向外迁移并通过强烈蒸发流失。

图6c显示了爆炒过程中原料颗粒水分损失和体积收缩率随温度的变化情况，可以观察到随着传热的进行水分损失趋势与体积收缩率相近，水分损失越大收缩率越大，但水分损失将逐渐大于收缩率。Rahman等[37]发现在新鲜鱿鱼的干燥过程中也会出现类似情况，主要原因是固体基质大量失水后提高了固体基质的玻璃态转换温度，由高弹态逐步转换为玻璃态，使得形变更难发生。在40至50 ℃间水分损失和体积收缩率出现拐点，与Briskey等[27]报道的肉的持水下降温度区间相符。图6c中试验值为Kovácsné等[38]观察冷冻肉沫馅水分损失随温度变化的实测值，与模拟值对比可知，在约40 ℃前模拟值与试验值差异明显，这是因为爆炒过程为非稳态传热，不同加热初始温度分布将使得两者内部传热出现差异，而本研究数值模拟研究对象为猪里脊肉肉柱，与肉沫馅存在孔隙率、渗透率等物性参数的差异造成偏离。因此，可利用水分损失与体积收缩率的相近趋势将含水率与收缩联系起来，作为评价烹饪品质的重要指标对颗粒烹饪品质开展研究。

2.2.3 温度分布与收缩现象

图6d中，40 s相较1 s时体积已大幅减小，随着传热持续进行，即使外部剧烈蒸发消耗了大量能量，余下能量仍迅速向内部热传导使内部温度迅速升高。烹饪达到160 s后，内部温度分布趋于均匀，表面被加热至沸点以上。这是由于水分损失造成表面含水率降低，表面蒸发减弱，传入能量远大于蒸发潜热。图6e显示了不同时间点由肉柱中心到外表层的温度空间分布，在30 s时存在较大的温度梯度，随着传热进行，温度梯度不断减小，温度曲线最右端点持续向左靠拢，反映了收缩现象；在60 s时中心温度65.7 ℃相较30 s中心温度30.1 ℃增大119%；在90 s后温度分布曲线趋平，内部温度梯度减小，中心温度与表面温度更为接近，蒸发现象减弱，表面被加热至沸点以上。收缩有利于传热使颗粒相对表面积增大，增大了传热效率，内部中心温度升高更快，内部温度更快趋于均匀；同时，结合图5b收缩对传质同样有促进作用，并使爆炒过程中颗粒内部产生正压力（图6a），促进调味物质向颗粒内的渗入。因此，控制收缩可以影响颗粒的传热和传质过程，有利于烹饪成熟和含水率、口感品质等优化，是烹饪爆炒技术优势的重要因素。

爆炒成品含水率越高，则肉显得多汁，口感好。在烹饪品质优化中，水分保持是正面指标。但在烹饪中，肉的水分流失是不可避免的。水分流失产生的收缩有利于提高爆炒升温速度，余冰妍[20]的优化研究表明，提高烹饪升温速度可以提高菜肴总体含水率。但随着传热进行收缩也增加了总过程的水分传质效率，使含水率下降。这样，出现了收缩同时正负面影响水分变化的复杂情况。值得注意的是，收缩是水分流失导致，而不是相反。因此，从烹饪品质优化上看，收缩总体上是有利于提高烹饪菜肴含水率。而烹饪爆炒中水分是核心品质指标，且变化剧烈，影响因素多，是热/质传递和烹饪品质优化的关键因素，收缩对其的影响值得进一步分析研究。

2.3 火候控制对成熟、品质的影响

在爆炒研究中，最大的困难是无法获得爆炒过程中随时间和空间位置变化的颗粒内部的温度分布，进而无法计算得到对应的成熟值，限制了其工艺优化。通过数值模拟可以获取颗粒内部的温度分布和水分分布，通过调整边界条件如fp、初始条件如特征尺寸和预热油温，以模拟不同火候控制，研究其对烹饪成熟、品质的影响，并定性和定量地分析，进一步为中式烹饪的自动化、工程化提供了理论基础，为工艺参数设定和优化提供指导。

爆炒烹饪食品的营养保持、咀嚼口感等品质与传热、含水率、形状尺寸密切相关，受火候控制的影响[1]。常见的火候强化手段有精细切割、油的预热和剧烈搅拌。本文使用M反映成熟，当M为0.5 min时猪里脊肉颗粒达到最佳成熟；水分与烹饪品质有关[39]，使用平均含水率、水分损失反映颗粒烹饪品质。

2.3.1 切割技术

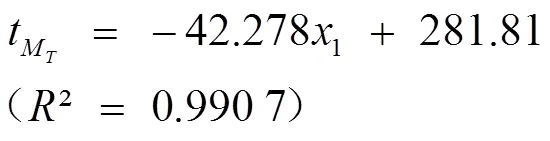
注：图6 a中0和0.5 mm分别为中心压力和距离中心0.5 mm处压力。

Note: In Figure 6a, 0 and 0.5 mm are center pressure and pressure at 0.5 mm from center respectively.

图6 爆炒过程模拟中颗粒内部变化

Fig.6 Particle internal changes during Chinese stir-frying simulation

因此，切割技术通过改变颗粒特征尺寸，影响加热介质对颗粒的传热效率，控制颗粒的成熟过程和烹饪品质。颗粒高度越小、中心温度上升越快，含水率下降越快，仅减小0.4 cm，内部传热与传质速率变化巨大。模拟表明，精细适宜的切割技术在爆炒过程对原料颗粒成熟和烹饪品质影响巨大，有利于提高升温速度，减小成熟时间，提升烹饪品质。

2.3.2 预热油温

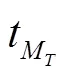
100 ℃较120 ℃油温处理，烹饪终点成熟时间缩短了33.3%，差异极显著（<0.01）；当增大到140 ℃后烹饪终点成熟时间缩短了14.5%，差异极显著（<0.01）。在相同成熟标准下，140 ℃高油温爆炒的水分损失率与较低油温相比基本没有变化（表3）。按原理，肉加热的温度越高，水分损失一定越大。这一现象是烹饪品质优化原理的后果，反映了烹饪品质优化的本质：升温速度的提高，使得中心冷点达到烹饪成熟时，水分还来不及流失。从动力学上说，烹饪成熟比水分流失对温度更为敏感。

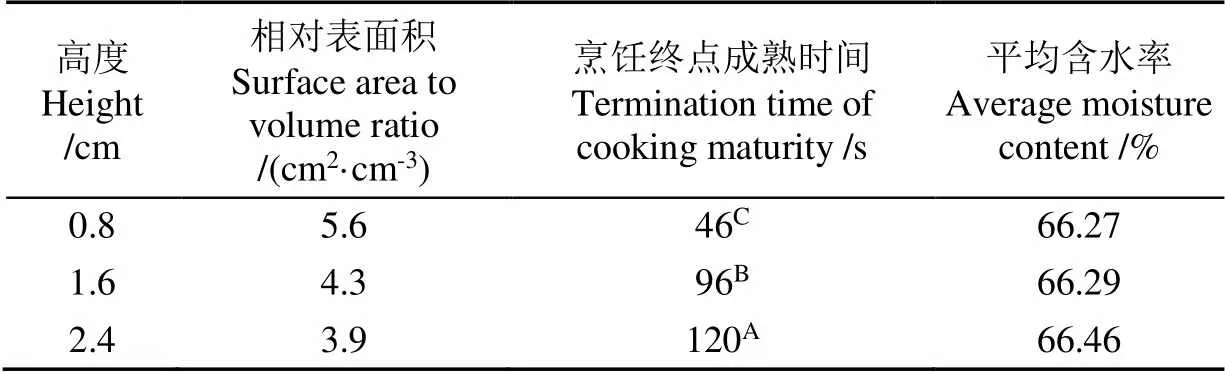
表2 切割技术对烹饪终点成熟时间与平均含水率的影响结果

注：图中同一指标中不同大写字母表示有极显著性差异（<0.01），下同。

Note: Different capital letters significant distinct differences (<0.01), the same as below.

与水分保持类似的品质还有口感、质构和营养保持等。因此，预热油温控制通过改变升温速率影响烹饪成熟和品质。预热油温越高，成熟所需时间越短，烹饪总体品质越好。在徐嘉[40]爆炒烹饪品质优化研究中也得到了相同的结论。由此推断，收缩是爆炒烹饪形成很高加热品质的技术优势之一。

2.3.3 搅拌操作

流体-颗粒对流换热系数（fp）表征单位面积上流体与颗粒食品表面间的传热速率，搅拌越剧烈，流体与颗粒食品之间的热交换更强，fp越大。张宏文[41]通过改变恒温油浴锅内流体流速，以模拟搅拌操作，使用TTIs法结合多孔介质热/质传递模型测量得到炸、炒典型烹饪过程的fp在250至1 375 W/(m2∙K)范围内。其中，典型烹饪过程是对实际烹饪工艺的简化，近似模拟烹饪环境，但与实际烹饪结果相比不会产生颠覆性影响。因此，选取200到1 000 W/(m2∙K)的fp范围，加热条件为120 ℃，其余定解条件不变进行数值模拟得图7c不同fp对颗粒中心温度和平均含水率的影响。由图可知，在爆炒过程中，对于同一初始温度的原料颗粒，fp越大，中心温度攀升更快，平均含水率下降更为迅速。这是因为fp的增大，提高了传热效率，在单位时间内，颗粒获得更多来自对流传热的能量。

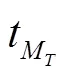
结合成熟值理论，当fp由200增大到600 W/(m2∙K)后，烹饪终点成熟时间缩短了13.5%，差异极显著（<0.01）；当增大到1 000 W/(m2∙K)后烹饪终点成熟时间缩短了10.9%，差异极显著（<0.01），这是由于fp增大使传热效率提高，颗粒的成熟过程被加速。图 7c中不同fp处理的M0.5 min对应时间点都位于含水率大幅下降之前，颗粒平均含水率差异较小，较初始含水率下降不大。这主要是由于爆炒中剧烈的搅拌加快了加热介质的流速，尽量保持加热介质与颗粒间的最大温度梯度，增强了传热效率。因此，搅拌操作提升了传热效率，增加了颗粒升温速率，使颗粒在含水率大幅减少前成熟，有助于改善颗粒口感和营养。

注：图7 a中0.8、1.6和2.4 cm为圆柱颗粒高度；图7 b中100、120和140 ℃为预热油温；图7 c中hfp200、600和1 000 W∙(m-2∙K-1)为液体一颗粒对流换热系数。

Note: In Fig.7a, 0.8, 1.6 and 2.4 cm are heights of cylinder particle; In Fig.7b, 100, 120 and 140 ℃ are temperatures of preheat oil; In Fig.7c, 200, 600 and 1 000 W∙(m-2∙K-1) are fluid-particle convection heat transfer coefficient.

图7 火候控制对颗粒烹饪成熟和品质的影响

Fig.7 Effect of “Huohou” controlling on particle cooked maturity and quality

表3 预热油温对烹饪终点成熟时间与平均含水率的影响结果

表4 搅拌操作对烹饪终点成熟时间与平均含水率的影响结果

3 结 论

1）基于多孔介质理论、非稳态传热原理、达西定律和菲克定律等，构建了视食品为含湿非饱和多孔介质、耦合收缩和相变过程的颗粒爆炒热/质传递数学模型，该模型有更好的准确性、鲁棒性。模型虽针对猪里脊肉构建，但其基于基础的能量、质量、动量平衡，考虑因素全面，覆盖性强，应用时只需改变参数即可适应大多数爆炒烹饪研究。因此，模型不受烹饪原料种类形状、尺寸和加热介质等的限制。由于爆炒是烹饪中最为复杂的过程，删减其中的部分本构方程及更换参数即可适用于大多数烹饪过程的数值模拟。该模型是广谱、全局、高效、低成本研究烹饪热/质传递的强有力手段，与品质动力学方程联用能适用于各种烹饪方式的最优操作参数寻找、工艺优化等场景。

2）数值模拟分析表明，颗粒收缩现象与水分损失呈正相关，对内部压力产生影响，收缩可增强传热和传质效率，内部温度更快趋于均匀，控制收缩可以控制颗粒的传热和传质过程，有利于品质优化，是烹饪爆炒技术优势的重要因素。

3）热/质传递数学模型可精确分析烹饪过程，用于自动烹饪设备设计，借助线性模型可预测成熟时间。结合成熟值理论开展的数值模拟表明，颗粒尺寸、表面换热系数和介质温度对烹饪成熟有显著影响，说明刀工切割、烹饪搅拌和油的预热是有效的火候调控手段。

[1]邓力. 中式烹饪热/质传递过程数学模型的构建[J]. 农业工程学报，2013，29(3)：285-292. Deng Li. Construction of mathematical model for heat and mass transfer process of Chinese cooking[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(3): 285-292. (in Chinese with English abstract)

[2]邓力. 烹饪过程动力学函数、优化模型及火候定义[J]. 农业工程学报，2013，29(4)：278-284. Deng Li. Kinetic functions, optimizing model and definition of “Huohou” for Chinese cooking[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(4): 278-284. (in Chinese with English abstract)

[3]邓力，金征宇. 液体-颗粒食品无菌工艺的研究进展[J]. 农业工程学报，2004，20(5)：12-21. Deng Li, Jin Zhengyu. Research advances in aseptic processing of liquid/particle foods[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(5): 12-21. (in Chinese with English abstract)

[4]Sanz-Serrano F, Sagues C, Feyissa A H, et al. Modeling of pancake frying with non-uniform heating source applied to domestic cookers[J]. Journal of Food Engineering, 2017, 195: 114-127.

[5]Singh A P, Singh A, Ramaswamy H S. Heat transfer phenomena during thermal processing of liquid particulate mixtures-a review[J]. Critical Reviews in Food Science and Nutrition, Taylor & Francis, 2017, 57(7): 1350-1364.

[6]Shi C, Guo H, Wu T, et al. Effect of three types of thermal processing methods on the lipidomics profile of tilapia fillets by UPLC-Q-Extractive Orbitrap mass spectrometry[J]. Food Chemistry, 2019, 298: 125029.

[7]Jiao Y, Liu Y, Quek S Y. Systematic evaluation of nutritional and safety characteristics of Hengshan goat leg meat affected by multiple thermal processing methods[J]. Journal of Food Science, 2020, 85(4): 1344-1352.

[8]Farabegoli F, Nesci S, Ventrella V, et al. Season and cooking may alter fatty acids profile of polar lipids from blue back fish[J]. Lipids, 2019, 54(11-12): 741-753.

[9]Bahar T, Boy V, Lemée Y, et al. Air impingement drying of foods: Modelling coupled heat and mass transfer and experimental validation[J]. Chemical Engineering, 2018, 70: 1957-1962.

[10]Fowler A J, Bejan A. The effect of shrinkage on the cooking of meat[J]. International Journal of Heat and Fluid Flow, 1991, 12(4): 375-383.

[11]Baik O D, Mittal G S. Heat and moisture transfer and shrinkage simulation of deep-fat tofu frying[J]. Food Research International, 2005, 38(2): 183-191.

[12]Akiyama T, Hayakawa K. Heat and moisture transfer and hygrophysical changes in elastoplastic hollow cylinder-food during drying[J]. Journal of Food Science, 2000, 65(2): 315-323.

[13]Costa R M, Oliveira F A R, Boutcheva G. Structural changes and shrinkage of potato during frying[J]. International Journal of Food Science and Technology, 2001, 36(1): 11-23.

[14]Mahiuddin M, Khan M I H, Kumar C, et al. Shrinkage of food materials during drying: current status and challenges[J]. Comprehensive Reviews in Food Science and Food Safety, 2018, 17(5): 1113-1126.

[15]Li X, Llave Y, Mao W, et al. Heat and mass transfer, shrinkage, and thermal protein denaturation of kuruma prawn () during water bath treatment: A computational study with experimental validation[J]. Journal of Food Engineering, 2018, 238: 30-43.

[16]廖小梅. 基于hfp测定的中式烹饪传热规律及分类特征研究[D]. 贵阳：贵州大学，2020. Liao Xiaomei. Chinese Cooking Heat Transfer Law and Classification Characteristics Based on hfp Measurement[D]. Guiyang: Guizhou University, 2020. (in Chinese with English abstract)

[17]周杰，邓力，闫勇，等. 烹饪传热学及动力学数据采集分析系统的研制[J]. 农业工程学报，2013，29(23)：241-246. Zhou Jie, Deng Li, Yan Yong, et al. Development of system on data acquisition and analysis of heat transfer and kinetics for Chinese cuisine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(23): 241-246. (in Chinese with English abstract)

[18]闫勇，邓力，何腊平，等. 猪里脊肉烹饪终点成熟值的测定[J]. 农业工程学报，2014，30(12)：284-292. Yan Yong, Deng Li, He Laping, et al. Determination of maturity value of fully cooked pork loin in cuisine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(12): 284-292. (in Chinese with English abstract)

[19]崔俊. 爆炒烹饪的 CFD 数值模拟及功率测定研究[D]. 贵阳：贵州大学，2017. Cui Jun. Simulation by CFD and Energy Consumption Analysis for Stir-Frying with Oil[D]. Guiyang: Guizhou University, 2017. (in Chinese with English abstract)

[20]余冰妍. 油传热烹饪过程的数值模拟及实验研究[D]. 贵阳：贵州大学，2019. Yu Bingyan. The Numerical Simulation and Experimental Study on the Cooking Processing with Oil Heat-Transfer[D]. Guiyang: Guizhou University, 2019. (in Chinese with English abstract)

[21]刘伟，范爱武，黄晓明. 多孔介质传热传质理论与应用[M]. 北京：科学出版社，2006.

[22]Datta A K. Porous media approaches to studying simultaneous heat and mass transfer in food processes. II: Property data and representative results[J]. Journal of Food Engineering, 2007, 80(1): 96-110.

[23]Sahin S, Sastry S K, Bayindirli L. Heat transfer during frying of potato slices[J]. LWT - Food Science and Technology, 1999, 32(1): 19-24.

[24]Ni H, Datta A K. Moisture, oil and energy transport during deep-fat frying of food materials[J]. Food and Bioproducts Processing, 1999, 77: 194-204.

[25]Ratti C, Crapiste G H, Rotstein E. A new water sorption equilibrium expression for solid foods based on thermodynamic considerations[J]. Journal of Food Science, 1989, 54(3): 738-742.

[26]Le C V, Ly N G, Postle R. Heat and mass transfer in the condensing flow of steam through an absorbing fibrous medium[J]. International Journal of Heat and Mass Transfer, 1995, 38(1): 81-89.

[27]Briskey E J, Cassens R G, Trautman J C. The Physiolocy and Biochemistry of Muscle as A Food[M]. London: The American Journal of the Medical Science, 1967.

[28]Feyissa A H, Adler-Nissen J, Gernaey K V. Model of heat and mass transfer with moving boundary during roasting of meat in convection-oven[C]//COMSOL Conference，https://cn.comsol.com/products, 2009.

[29]Joardder M U H, Kumar C, Karim M A. Multiphase transfer model for intermittent microwave-convective drying of food: Considering shrinkage and pore evolution[J]. International Journal of Multiphase Flow, 2017, 95: 101-119.

[30]Lewis M J. Physical Properties of Foods and Food Processing Systems[M]. Elsevier, 1990: 222-223.

[31]Bear J. Dynamics of Fluids In Porous Media[M]. American Elsevier Publishing Company, 1972(1): 113-114.

[32]Baiocchi C. Problemes a frontiere libre en hydraulique: milieux non homogenes[J]. Annali della Scuola Normale Superiore di Pisa-Classe di Scienze, 1978, 5(3): 429-453.

[33]Barbera S, Tassone S. Meat cooking shrinkage: Measurement of a new meat quality parameter[J]. Meat Science, 2006, 73(3): 467-474.

[34]王磊，邓力，李慧超，等. 基于CFD数值模拟的豆腐干软罐头杀菌工艺优化[J]. 农业工程学报，2017，33(21)：298-306. Wang Lei, Deng Li, Li Huichao, et al. Optimization of sterilization process of retort pouch tofu cake based on CFD numerical simulation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(21): 298-306. (in Chinese with English abstract)

[35]Costa A. Permeability-porosity relationship: A reexamination of the Kozeny-Carman equation based on a fractal pore-space geometry assumption[J]. Geophysical Research Letters, 2006, 33(2): 1-5.

[36]Chemkhi S, Jomaa W, Zagrouba F. Application of a coupled thermo-hydro-mechanical model to simulate the drying of nonsaturated porous media[J]. Drying technology, Taylor & Francis, 2009, 27(7/8): 842-850.

[37]Rahman M S, Perera C O, Chen X D, et al. Density, shrinkage and porosity of calamari mantle meat during air drying in a cabinet dryer as a function of water content[J]. Journal of Food Engineering, 1996, 30(1/2): 135-145.

[38]Kovácsné Oroszvári B, Sjöholm I, Tornberg E. The mechanisms controlling heat and mass transfer on frying of beefburgers. I. The influence of the composition and comminution of meat raw material[J]. Journal of Food Engineering, 2005, 67(4): 499-506.

[39]邓力. 炒的烹饪过程数值模拟与优化及其技术特征和参数的分析[J]. 农业工程学报，2013，29(5)：282-292. Deng Li. Numerical simulation, optimization, study of technical features and operational parameters for Chinese cuisine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(5): 282-292. (in Chinese with English abstract)

[40]徐嘉. 中式烹饪油炒火候原理初探[D]. 贵阳：贵州大学，2019. Xu Jia. A Preliminary Study on the Principle of the Control of Cooking Time of Stir-Frying Processing in Chinese Cuisine[D]. Guiyang: Guizhou University, 2019. (in Chinese with English abstract)

[41]张宏文. 基于成熟值理论的中式烹饪关键传热规律研究[D]. 贵阳：贵州大学，2019. Zhang Hongwen. Chinese Cooking Key Heat Transfer Law Based on Maturity Value Theory[D]. Guiyang: Guizhou University, 2019. (in Chinese with English abstract)

Simulation and experimental validation of heat and mass transfer during Chinese stir-frying considering shrinkage

Xie Le1, Deng Li1※, Li Jingpeng1,2, Zeng Xuefeng1, Yan Yong3, Shi Yu1, Su Jieyu1

(1.,,550025,; 2.,,214122,; 3..,550025,)

Food stir-frying is one of the most popular and widely used cooking method to prepare vegetables, particularly in southeast Asian countries. This quick food preparation method is used the heat transfer from a hot pan surface to foods, using a small amount of cooking oil. To promote the development, automation, and standardization of Chinese cuisine, it is necessary to carry out a systematic investigation for the heat transfer and the quality changes of food during the cooking process. Numerical simulation can offer one way to explore the heat and mass transfer process of food particles during the food stir-frying. In this study, a heat and mass transfer model was developed, including multiphase coupling phase transition and shrinkage, in order to simulate the stir-frying process of food hygroscopic porous medium, using the porous media theory, Fourier's law, Newton's cooling law, and Darcy's law. An emphasis was also placed on the mechanism of heat transfer, and the variation in maturity and quality of food particles during the Chinese cuisine process. The model considered the non-equilibrium evaporation and shrinkage formulation, energy, momentum and mass conservations of water, and gas governing equations, thereby finally solved by finite element method. The accuracy of model was verified by the temperature history, moisture content, and volumetric shrinkage rate of stir-fried pork loin. The results indicated that the accuracy and robust properties of this model greatly increased after considering the shrinking process. Some parameters, including the water evaporation rate of particle surface, volumetric shrinkage rate, pressure variations, moisture content and temperature distributions, were simulated to reveal the mechanisms of heat and mass transfer inside the food particle for the stir-frying process. The simulation results showed that the main reason for shrinkage was the water loss that induced by strong convection heat transfer. The surface evaporation rate can increase the rate of moisture loss and volumetric shrinkage. The particle internal pressure also determined the volumetric shrinkage. Since the function of volumetric shrinkage rate was analogous to that of water loss rate, the moisture content and shrinkage were associated with an important indicator to evaluate the cooking quality of food particles. Additionally, the heat transfer efficiency of particles was greatly enhanced by shrinkage, because of the increasing surface area to volume ratio. The shrinkage can be used to improve the overall moisture content of food particles, if evaluated from the perspective of cooking quality. Combined with the maturity value theory, further investigation also made on the effect of controlling methods of “Huohou” on the maturity and quality of food particles. The finer cutting technique of food particles can mainly determine to increase in efficiency of heat and mass transfer and internal heating rate, whereas, to decrease in average moisture content. The stirring operations can be vigorous, as the preheating oil temperature increased. The food particles can reach its maturity values, before the average moisture content rapidly decreased under the appropriate “Huohou” controlling. Thus, it infers that the control of “Huohou” can be used to dramatically reduce the average time of food particles for reaching cooking maturity termination, indicating a significant (<0.01) effect on the cooking quality. The finding can bring important advantages to obtain food particles with better cooking quality during the food stir-frying process.

numerical simulation; models; moisture; Chinese stir-frying; shrinkage; heat and mass transfer

谢乐，邓力，李静鹏，等. 考虑收缩的爆炒热/质传递过程模拟与验证[J]. 农业工程学报，2020，36(18)：251-262.doi：10.11975/j.issn.1002-6819.2020.18.030 http://www.tcsae.org

Xie Le, Deng Li, Li Jingpeng, et al. Simulation and experimental validation of heat and mass transfer during Chinese stir-frying considering shrinkage[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(18): 251-262. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.18.030 http://www.tcsae.org

2020-05-25

2020-08-04

国家自然科学基金（31660449, 31860443）；贵州省科技计划（黔科合重大专项字[2015]6004号）；贵州省科技计划（黔科合支撑[2017]2556）；贵州省科技计划（黔科合农G字[2014]4016号）；国家重点研发项目（2018YFD0401200）

谢乐，主要研究食品热加工的数值模拟。Email：xie.le@outlook.com

邓力，博士，教授，主要研究方向为自动烹饪、复杂食品加工过程的数值分析、现代杀菌技术及挤压技术。Email：denglifood@sohu.com

10.11975/j.issn.1002-6819.2020.18.030

TS201.1

A

1002-6819(2020)-18-0251-12