基于粒子群算法的车辆半主动悬架模糊PID控制的优化研究
,,
(1.青岛科技大学机电工程学院,山东 青岛 266061;2.一汽解放青岛汽车有限公司,山东 青岛 266043)
0 引言
道路的不平整会引起汽车在行驶过程中的不规则振动,对汽车的行驶平顺性和操纵稳定性有很大的副作用。此外,车轮与地面之间会产生动载荷,也影响车辆行驶稳定性。悬架可以将车架与车轴弹性地连接起来,如果路面不平引起一定程度的振动,悬架可以起到缓冲作用,减弱从轮胎传递到车身的振动。相较于主动悬架,半主动悬架具有价格较低、技术要求较低、可靠性高的优点,在现代车辆上广泛应用。半主动悬架可根据路面状况和汽车响应特性对可控阻尼的阻尼力进行适时调节,使悬架在各种路面情况下达到最佳减振效果。
为了得到性能更好的半主动悬架,王威等[1]以车身垂直振动加速度为控制目标,将遗传算法与模糊PID控制策略融合,有效减小了车身垂直振动加速度。杨柳青等[2]在电磁阀减振器力-速度特性试验基础上,提出一种基于输入饱和的滑模控制策略,车辆的垂向特性得到有效改善。郭全民等[3]利用粒子群算法的并行全局搜索能力对PID控制参数KP、KI、KD进行整定,以此来改善汽车半主动悬架PID控制的性能。严天一等[4]利用粒子群优化算法对模糊混合控制器的隶属度函数和模糊控制规则同时进行优化,提高了半主动悬架系统的综合性能。赵强等[5]利用遗传算法的全局优化能力和并行能力优化模糊PID控制器的量化因子及其PID参数的修正系数,得到一组最佳的PID参数。Cao等[6]针对汽车半主动悬架系统,提出了一种基于区间模糊隶属函数的扩展模糊逻辑控制器,对半车主动悬架系统的仿真研究表明,该控制器的性能优于传统的模糊逻辑控制器。Liu等[7]提出了一种新的主动跟随模糊输出反馈滑模控制方法,用于实际车辆半主动悬架系统。楼少敏等[8]基于滑模理论设计了7自由度的整车半主动悬架系统的滑模控制器,悬架性能得到大幅提升。本文利用粒子群算法的全局并行搜索能力对模糊PID控制器进行优化,并对比分析在相同路面情况与行驶速度下,不同控制器对悬架性能的优化效果。
1 动力学模型建立
1.1 半主动悬架模型建立
1/2车辆动力学模型具有4个自由度,分别是前轮垂向位移、后轮垂向位移、车身垂向位移及车身俯仰运动。1/2车动力学模型如图1所示。
1/2车辆半主动悬架数学模型为
(1)
其中
(2)
图1和式(1)、式(2)中,k1f为前轮刚度系数;k1r为后轮刚度系数;m1f为前轮非簧载质量;m1r为后轮非簧载质量;c2f为前悬架阻尼;c2r为后悬架阻尼;k2f为前悬架刚度;k2r为后悬架刚度;f1f为前悬架可控阻尼;f1r为后悬架可控阻尼;m2为车身质量;I为转动惯量;L为轴距;L1为车身质心到前轴的距离;L2为车身质心到后轴的距离;x3为车身质心的垂直位移;x1f为前悬架非簧载质量垂直方向的位移;x1r为后悬架非簧载质量垂直方向的位移;x2f为前车身垂向位移;x2r为后车身垂向位移;x0f为前轮的路面不平度;x0r为后轮的路面不平度;F1r为后悬架弹簧力;F1f为前悬架弹簧力。其中,各个参数数值如表1所示。

表1 1/2车辆悬架参数
1.2 路面模型建立
本文使用有限带宽白噪声法建立路面Simulink模型。其中随机路面输入函数表达式为
(3)
n0为参考空间频率,取值0.1 m-1;Gq(n0)为路面不平度系数,本文选取B级路面,其数值为64×10-6m3;v为行驶速度,本文取行驶速度为30 km/h;w(t)为白噪声。路面Simulink模型如图2所示。
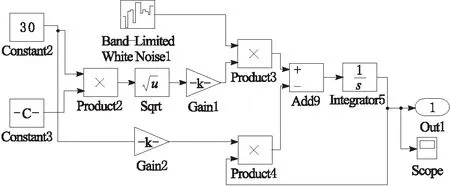
图2 路面Simulink模型
2 模糊PID控制系统
2.1 PID控制器结构
传统的PID控制器由比例(P)、积分(I)和微分(D)组成,首先根据系统的偏差,利用上述3个分量计算控制量,然后进行控制。它具有控制结构和算法简单、稳定性好、精度高、响应速度快、适应性广等特点,在工业控制领域得到了广泛的应用。
2.2 Fuzzy-PID控制器结构
Fuzzy-PID主要由传统PID控制器和模糊化模块组成。在数据分析和参数选择上,模糊自适应PID控制可以在原算法的基础上,通过输入误差变化率ec和误差e,并用模糊规则推断参数,找到相应的矩阵并进行分析。1/2车辆半主动Fuzzy-PID控制悬架是用2个模糊PID控制器分别控制前悬架和后悬架,在传统PID控制器的基础上,采用模糊逻辑推理对PID参数进行调整,并采用PID算法得到系统输出[9]。1/2车辆半主动悬架系统Fuzzy-PID控制器结构如图3所示。

图3 模糊控制PID结构
2.3 模糊控制规则设置
将系统误差e的变化范围设置为[-6,6],误差变化率ec的变化范围为[-3,3],然后建立模糊控制规则表,分别如表2、表3和表4所示。

表2 ΔKP模糊控制规则
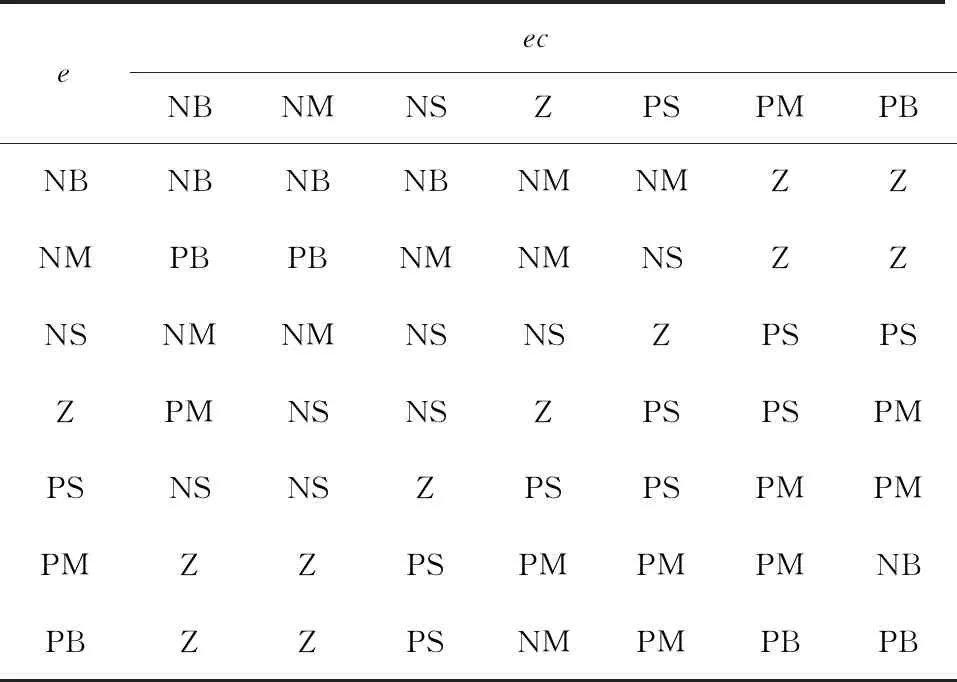
表3 ΔKI模糊控制规则

表4 ΔKD模糊控制规则
3 基于粒子群算法优化模糊PID控制器

(4)
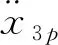
粒子群中的粒子在空间中的位置、速度更新表达式为:
vj(t+1)=ωvj+c1r1[Pj(t)-xj(t)]+c2r2[Pw(t)-xj(t)]
(5)
xj(t+1)=xj(t)+vj(t+1)
(6)
ω为惯性权数;c1和c2为加速系数;r1和r2为0~1范围内的随机数。
粒子群算法对悬架系统的模糊PID控制器优化流程如图4所示。
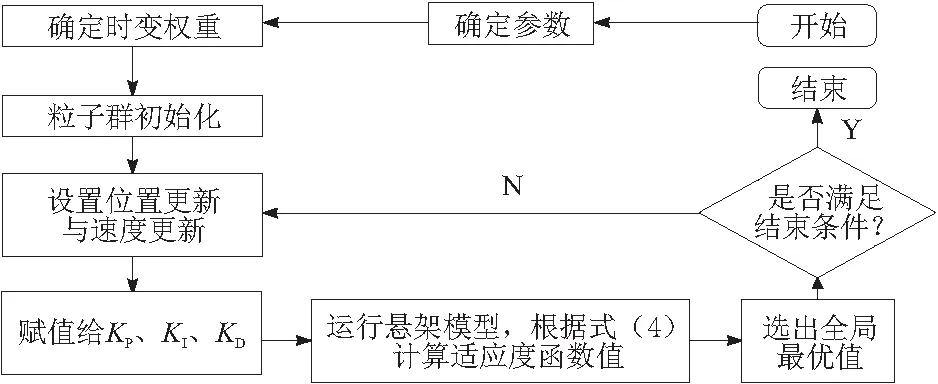
图4 模糊PID控制器优化流程
a.确定的参数值包括惯性因子、加速常数、维粒子群规模、最大迭代次数、最小适应值。
b.确定时变权重。时变权重的确定公式为
w(i)=wmax-i(wmax-wmin)/G
(7)
wmax与wmin为权重的最大值与最小值;i为迭代次数;G为最大迭代次数。
c.粒子群初始化。设置粒子群体规模为n搜索范围为一个S维的目标搜索空间中,其中第i个粒子可表示为
Xi=(xi1,xi2,xi3,…,xiS),i=1,2,3,…,n
(8)
每一个粒子的位置都是一个潜在的解,将Xi代入目标函数即可计算出其适应值,根据适应值的大小衡量解的优劣。粒子最初的飞行速度表示为
vi=(vi1,vi2,vi3,…,viS),i=1,2,3,…,n
(9)
粒子最初位置表示为
Pi=(pi1,pi2,pi3,…,piS),i=1,2,3,…,n
(10)
d.速度与位置更新。在找到最优值之前,粒子根据式(11)更新速度,根据式(12)更新位置:
vis(t+1)=vis(i)+c1r1(t)(pis(t)-xis(t))+c2r2(t)(pg(t)-xis(t))
(11)
xis(t+1)=xis(t)+vis(t+1)
i=1,2,3,…,ns=1,2,3,…,S
(12)
Vis(t)为粒子i第t次迭代速度的第s维分量;c1、c2为学习因子;r1、r2为相互独立的伪随机数;pis为粒子最优位置;pg为粒子群最优位置;xis(t)为粒子i第t次迭代位置的第s维分量。
e.迭代求解,选取全局最优值。根据式(4)求出粒子群适应度函数值,判断是否为全局最优解,并满足临界条件。若满足,则退出算法,输出最佳个体值。若不满足,则重新更新粒子群速度与位置,代入粒子群适应度函数继续求解。
4 仿真结果与分析
为了验证PSO Fuzzy-PID 控制器有效提升悬架性能,在相同的路面条件与行驶速度下,选择与被动悬架、PID控制悬架与Fuzzy-PID控制悬架的性能进行比对,比对结果如表5所示。
由表5可以看出,前轮动载荷、前悬架动挠度、车身垂直加速度、俯仰角加速度、后轮动载荷、后轮动挠度的均方根值相较于被动悬架,PID控制使悬架性能提升了14.51%、4.89%、13.83%、15.88%、16.83%、5.74%;Fuzzy-PID控制使悬架性能提升了20.08%、16.88%、17.67%、19.38%、17.56%、17.23%;PSO Fuzzy-PID控制使悬架性能提升了30.06%、27.54%、28.01%、29.54%、28.07%、27.69%。仿真结果表明,PSO Fuzzy-PID控制的半主动悬架的行驶平顺性和操纵稳定性要明显优于PID控制和Fuzzy-PID控制,并且悬架性能得到大幅提升。

表5 各控制方法仿真结果对比
5 结束语
利用粒子群算法的并行全局搜索能力,以提升悬架性能为目标对Fuzzy-PID控制器进行优化,克服了Fuzzy-PID控制中无法使悬架性能达到最优的缺点。通过对各控制方法的仿真结果对比可以看出,相较于传统PID控制和Fuzzy-PID控制,PSO Fuzzy-PID控制可以大幅降低车轮动载荷、悬架动挠度、俯仰角加速度与车身垂直加速度,提高了汽车行驶平顺性和操纵稳定性,悬架性能得到大幅改善。

