基于改进型蜻蜓算法的停电计划优化方法

，，，，，

(1.广州供电局有限公司，广东 广州 510620；2.北京清大科越股份有限公司，北京 100084)

0 引言

随着我国能源转型的不断深入和特高压的快速发展，电力系统规模、电网结构和电力现货交易市场范围都处于不断扩大的阶段。电网整体运行逐步向经济、环保、智能化方向转变，各种电力服务综合跨度的难度急剧增加，尤其是调度中心的停电管理和计划维修[1-3]。电力系统中普遍采用的计划维修又称定期维修，要求达到预定的设备周期，但维修周期、维修项目和进度安排管理要根据经验来预期，导致检修人员更难确定维修申报的有效期，留下不必要的安全隐患[4-6]。同时由于主网设备检修停电组合呈指数增长，必须考虑更多的经济、环保、智能化布局等影响因素[7-9]，因此如何优化停电方案，使得有限的人力、物力资源得到最有效的利用，以提高停电检修效率，就显得尤为重要。

停电计划的核心内容是对电力设备停电时段和工作项目的不同周期安排的管理，包括年、月(周)、日等。停电计划应以优化资源配置、实施国家能源战略等为基本要求，同时保证电网安全运行和用电可靠性[10]。因此从本质上来讲，停电计划就是一个多目标优化问题，而停电检修过程中对于电网安全运行和用电可靠性的要求，则是多目标优化问题中的约束，可以采用带约束的多目标优化模型来求解[11]，通过使整体目标函数达到极小值或者极大值，求解此时对应的模型输入参数，就可以得到停电计划的最优解[12]。

模型的求解结果通常取决于算法效率和精度，特别是采用传统极值求解算法时，如果模型初值设置不够准确，容易导致梯度消失、爆炸或者陷入局部最优的问题[13]。因此研究人员采用群智能算法求得优化问题的全局最优解，例如粒子群、遗传算法、模拟退火等[14-16]，但采用群智能算法处理电网调度和停电规划时，由于电网结构复杂，需要采用较多的群个体数，导致算法收敛速度慢、迭代至指定精度所需时间长等问题[17]，限制了停电检修计划制定的效率和精度。

为此本文建立了年度停电计划安排的多目标优化模型，提出了一种改进型蜻蜓算法，求解停电检修多目标优化模型的Pareto最优解集，采用IEEE案例，仿真对比了本文提出的算法与其他2种算法的收敛速度、精度和效率，研究结果可为电网智能调度和停电检修计划智能算法的设计提供参考。

1 停电计划模型

本文在实际停电计划管理的基础上，结合未来的状态网络拓扑结构，基于停电增量、冲突风险、供电约束、设备健康状态、停电协调，停电窗口和设备维护的最大时限等停电计划约束；充分考虑停运计划的可靠性、经济性、分配均衡性和储备性4个优化目标，建立了停电决策模型。

1.1 优化目标函数

停电优化的总体目标，由年度停电管理计划的可靠性、经济性、分配均衡性和储备性构成,其函数表达式为

F=f1+f2+f3+f4

(1)

f1为可靠性指标；f2为经济性指标；f3为分配平衡指数；f4为储备指数；F为问题的最优解。

1.1.1 可靠性指标

可靠性指标用于量化电力供给的可靠性的稳定性，计算公式为

(2)

n为该区域内电网节点的总数；φ为用电户总数；Tid为该区域内用电户长时间停电的时长。

1.1.2 经济性指标

停电经济性指标的数学模型为

(3)

φ为停电设备序列；Cp为电价；QLOL，i为用电设备序列中每一个用电设备i停电造成的负荷损失；pi为用电设备i停电期间造成的功率损失；μi为用电设备i的停电状态。

1.1.3 分布平衡性指标

分布平衡性指标的数学模型为

(4)

1.1.4 储备指标

储备指标的数学模型为

(5)

φ为备用设备序列；Qit为停电期间t内备用设备i的备用容量；ρit为停电时的备用容量率。

1.2 约束条件模型

优化模型采用的约束条件中，功率削减增量、冲突风险和供电约束是强制性约束条件，设备健康状态和设备维护的最大时限是中性约束条件，功率削减和停电协调约束是弱约束条件。

1.2.1 功率削减增量约束

功率削减量增量约束的计算公式为

(6)

ε为设备停电后，与之相关的其他设备；Qi为设备测量量；E1为测量上限；Es是测量的下限；stateb是断路器或者开关的状态。

1.2.2 冲突风险约束

冲突风险约束为

(7)

Di为设备A切断后再断开开关的风险；Dj为设备B切断后再断开开关的风险；Dk为设备B和设备A同时切断的风险值。

1.2.3 供电约束

供电约束表达式为

Ek∈θ

(8)

Ek为需要在一定时间内停电的设备；θ为一定时间内需要保护的设备。

1.2.4 设备健康状态约束

本文采用系统设备综合健康指数计算模型[7]及其设备健康指标作为约束条件，其数学模型为

(9)

n为设备数；m为特征参数数；ωi为参数的权重，可通过层次分析法确定；ρit为特征参数的权重；hij(t)为设备i的特征参数对应的健康指数。根据健康指数，按如下公式对约束停电计划的优先级进行划分

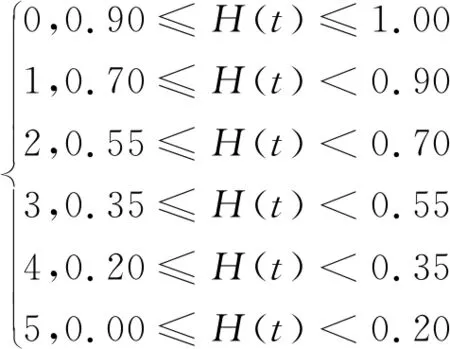
(10)

0代表设备健康状况设备非常好；1代表设备健康状态良好，适合长期运行；2代表设备具有异常情况，不适合长期运行；3代表设备情况更加异常；4代表设备处于严重异常状态，应在一周内停止并进行维修；5是设备不能运行，应立即安排维修。

1.2.5 设备维修的最长时限

设备维修时间定义为

t≤Si

(11)

t为设备i停电维修的时长；Si为设备维修的最大时间限制。

1.2.6 断电时长窗口

断电时长窗口为

ti∈Ti

(12)

ti为设备停电维修的周期；Ti为设备全年检修时间。

1.2.7 断电协调约束

断电协调约束计算公式为

Si=Sj

(13)

Si和Sj分别代表设备i和设备j的停电周期。

1.3 停电计划优化模型

停电计划的优化和策略制定本质上是一个典型的多目标优化模型，本文引入帕累托最优化的思想求解停电计划的多目标优化模型。

1.3.1 多目标蜻蜓算法

蜻蜓算法主要有以下几个主要部分构成：

a.目标函数拆分。进行目标函数拆分的公式为

(14)

X代表当前设备的位置；Xj代表相邻单元位置j；N代表相邻个体的数目。

b.初值标准化。按如下公式进行初值标准化

(15)

vj代表独立个体j的移动速度。

c.聚合过程。按如下公式进行单元聚合

(16)

X为当前设备的位置；Xj为相邻单元位置j；N为相邻个体的数目。

d.捕猎过程。按如下公式模拟捕猎过程

Fi=X+-X

(17)

X+为猎物所在位置。

e.自然天敌限制。按如下公式定义自然天敌限制

Ei=X-+X

(18)

X-为自然天敌的位置。

利用步长向量△X和位置矢量X来描述人工蜻蜓在搜索空间中的位置和速度的更新，其中步进矢量的描述方法与PSO算法相似。

本文在此处以一维数组的位置更新为例叙述其数学过程：

ΔXt+1=(sSi+αAi+cCi+fFi+eEi)+wΔXt

(19)

Xt+1=Xt+ΔXt+1

(20)

s为分离步的权重；Si为个体i的分离程度；α为目标权重；Ai为独立个体i的目标级别；c为聚集权重；Ci为个体的聚集度；F为捕食系数；Fi为个体i的猎物位置；e为自然天敌系数；Ei为个体i自然天敌的位置；w为惯性系数；t为迭代次数。

1.3.2 改进型多目标蜻蜓算法

为了提高Pareto解集的分布均匀性和种群多样性，本文引入了拥挤距离下的档案维护和生态位共享机制。

a.拥挤距离下的外部储备维护。基于拥挤距离的定义，对目标函数的所有最优解进行排序，并且针对优化解X和目标维数N的函数P(X,n)进行标注和排序，将相应的目标函数值标识为g(P(X,n))，在储备进行动态维护时，如果位置信息P(X,n)被删除，则还有位置P(X,n)+1和P(X,n)-1会受到影响，其最优解的拥挤分量可以表示为：

f(P(X,n)+1)=lg(P(X,n)+1)-g(P(X,n)-2)

(21)

f(P(X,n)-1)=lg(P(X,n)+2)-g(P(X,n)-1)

(22)

基于上述存档信息删除的影响特性，本文删除了满足外部存储更新过程中最小拥挤距离的最优解，并计算了删除解的受影响拥挤分量；再更新拥挤距离，提高最优解决方案的储备规模，以增强个体密集区的密度。

b.生态位共享。通过生态位共享机制，可定义外部储备中个体Xi的适应度为

(23)

NS为生态位中的个体数量；Si为个体的共享程度；Si定义为

(24)

fsh(dij)为个体Xi和Xj之间的分享函数，其公式定义为

(25)

α为代表函数的形状；σshare为预先指定的共享距离；dij为个体Xi和Xj之间的欧氏距离，表达式为

(26)

本文利用个体共享度和小生境个体数的特点，提出了正反馈方法，降低了种群中相似个体的整体适应度，使得算法在迁移过程中选择相似个体的概率增大，从而减少了解陷入局部最优的问题。

1.4 基于DMODA算法的停电计划模型

基于DMODA的算法的停电计划制定，按如下步骤进行：

a.得到所有停电设备及其电气参数和拓扑关系。得到电价和维修资源在时间段内进行优化配置的预测结果。计算供电约束、设备健康约束、停电窗口约束、设备检修最大时限约束，并计算未编制计划的停电协调约束。

b.参数初始化。随机生成种群的初始位置和速度，设置外部储备的最大容量、最大迭代次数和所有权重的初始值。

c.计算每个个体的目标函数。

d.根据Pareto最优关系，建立解决方案集，添加外部储备，根据外部储备容量选择是否进行动态维护。

e.根据生态位共享机制，选择个体并更新权重因子和半径参数。

f.根据约束函数和目标函数值的后移和低优先级方案。

重复步骤c～e。如果达到最大迭代次数，则将所有解决方案输出到外部储备中。

2 算例分析

本文以IEEE RTS-79为例，实验验证该优化方法的可行性。计划停运和维护的线路信息如表1所示，其中bi代表IEEE RTS-79系统中母线的编号；ei代表系统中的电源编号；li代表系统中子线路编号；维修周期为3个月，其中线路1和线路6不能在同一时期检修；线路维护费用为35 000元，节假日双倍；维修工作的上限为4组/d，每天检修的设备组不能超过4次。

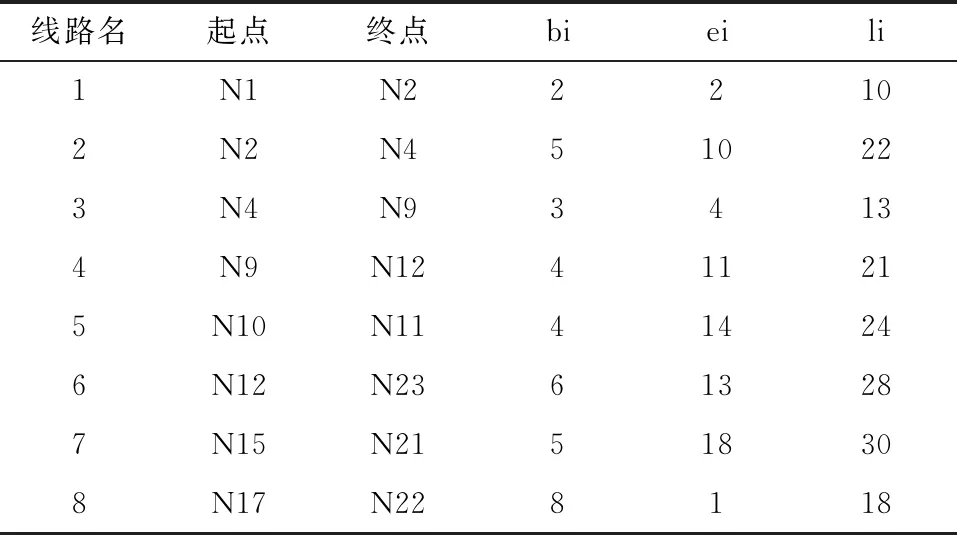
表1 线路检修信息

本文采用MOPSO和MODA算法与本文提出的算法作为对比，计算时3种算法的种群数量都为100；外部存储容量为200；最大迭代次数为500。仿真计算结果如图1所示。

由图1可知，选取相同的初始计算参数时，采用本文提出的算法仅需230次迭代就能将最优解的范数将至接近0；而采用MOPSO算法或者MODA算法计算，都需要至少400次迭代计算采用达到相同精度，并且采用MOPSO算法时其收敛曲线在迭代至200次时还出现了发散的现象，这是由于初始值选取不合理导致的。可见本文提出的算法在稳定性、收敛速度方面都具有最好的效果。

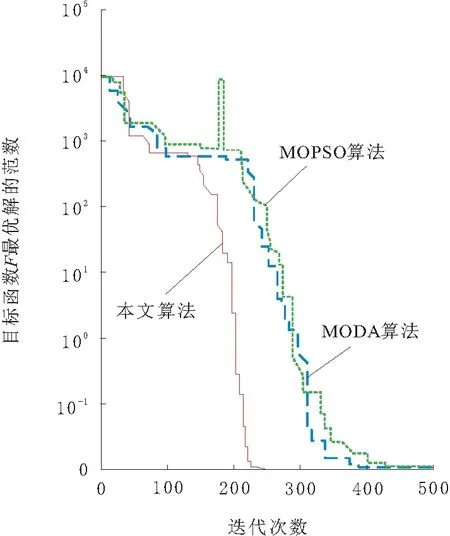
图1 不同算法收敛性示意

3 结束语

改进型蜻蜓算法，求解停电检修多目标优化模型的Pareto最优解集，采用IEEE案例，仿真对比了本文提出的算法与MODA、MOPSO 2种算法的收敛速度、精度和效率。结果表明本文提出的优化算法可在解精度达到相同要求的基础上，将迭代步数缩短一半，极大地提高了停电检修计划制定的效率。