散点状危险天气区域下终端区进场空域利用率

张兆宁，徐子航

（中国民航大学空中交通管理学院，天津 300300）

随着航空业的发展，空域拥挤和航班延误等问题也越来越突出。计算空域利用率，准确评估空域使用情况，可为安全合理地使用空域，缓解拥挤、延误等问题提供依据。在空域的实际运行中，空域利用率会受到天气因素影响，尤其是危险天气，终端区处于航路的汇合处，飞行活动复杂，受危险天气的影响更为明显。因此，准确评估危险天气下的终端区空域利用率具有重要意义。

国内外关于空域利用率的研究取得了一定成果。目前，对于危险天气下空域利用率的研究较少，现有的空域利用率研究基本只考虑了正常天气下的情况。Bloem 等[1]通过贪婪启发式算法优化空域利用率；Xue[2]采用“时空图”理论分析空中走廊的利用率；Sheth 等[3]从瞬时占用率和空间占用率角度评估了空中高速路利用率；Zhang 等[4]从时间、空间、容量等角度量化空域利用率并建立模型；施和平[5]采用实际被利用的空域与允许利用的空间之比表示空域利用率；张波等[6]从时间、空间、容量3 个方面建立指标体系，采用灰色关联分析法计算中长期空域利用率；王萍等[7]在灰色关联度的基础上，采用主成分分析法计算各年的空域利用率；李印凤等[8]利用层次权重决策分析评价终端区利用率等级；王鹏鹏等[9]将改进的灰色绝对关联度与主成分分析法结合，建立了终端区利用率模型；张兆宁等[10-12]分别针对航路、终端区建立了短时利用率模型，又基于熵值法评估了终端区空域利用率。从以上研究可看出，对于空域利用率的评估模型，主要分为两个方面：一方面是从建立评估指标体系的角度出发确定利用率等级或计算利用率；另一方面是在考虑空域结构及空域运行过程的基础上，从时间、空间和流量、容量等角度建立利用率评估模型。而目前关于危险天气下的空域利用率评估研究较少。

在已有研究基础上，考虑危险天气因素对空域利用率的影响，针对散点状危险天气区域，当终端区进场空域受其影响时，借助最大流最小割定理，得出散点状危险天气区域对容量的影响，从流容比角度，考虑时间、空间的限制，建立散点状危险天气区域下的终端区进场空域利用率模型，并验证其有效性。

1 相关概念

1.1 航空危险天气

航空危险天气指影响飞行安全的所有天气现象，主要包括雷暴、飑线、龙卷、风切变等[13]。影响终端区的危险天气主要为雷暴和风切变。根据形状及分布特点，危险天气区域可分为3 类：块状、散点状及带状[13]。针对终端区受散点状危险天气区域的影响，对其进场空域利用率进行研究。散点状危险天气区域，即在航线两侧无规则分布的多个小尺度危险天气区域，影响的航路点为2～3 个，如图1所示。

1.2 最大流最小割定理

最大流最小割定理主要应用于网络中最大流的求解，定理指出在任一网络G 中，从源点（S）到汇点（T）的最大流量等于分离源、汇的最小割的容量[14]。

Strang[15]对最大流最小割定理进行扩展，适用范围由网络扩展到了多边形，源和汇由两点变成了多边形的两条边，如图2所示，黑色部分为限制区，无法通过。最小割是整个网络的瓶颈，决定了整个网络的最大通过能力。Gewali 等[16]进一步得出割容量与空域边界和飞行受限区间的距离成正比。当终端区出现散点状危险天气区域时，可将航空器的通过抽象成连续流在多边形网络中的最大流最小割问题。

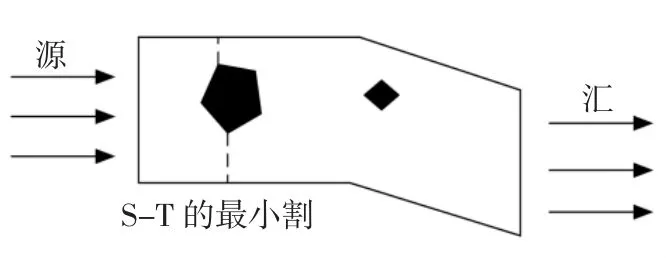
图2 最大流最小割示意图Fig.2 Schematic diagram of maximum flow and minimum cut

2 模型构建

2.1 问题描述

当终端区出现散点状危险天气区域时，某些航线或空域会无法使用，飞机通过选取不受影响的路线绕过危险天气区域。考虑到安全问题，绕飞方式为侧向绕飞。不同于块状危险天气区域的绕飞，散点状危险天气区域的绕飞相对复杂，除了从整个区域两侧绕飞外，如果危险天气区域间的距离符合条件，在某些条件下绕飞路线可从中间穿过。当出现散点状危险天气区域时，终端区空域的容量、流量都会受到影响。在研究散点状危险天气下的终端区进场空域利用率时，可通过最大流最小割的扩展定理确定容量的变化，从而建立终端区进场空域利用率模型。

2.2 散点状危险天气下的容量变化

空域边界与危险天气区域的距离及危险天气区域间的距离对容量影响最大，因此，在建立进场空域利用率模型之前，要明确散点状危险天气对进场空域的影响，从而确定散点状危险天气下进场容量的变化。

1）危险天气区域间的距离

关于距离的计算，可参考文献[17]提出的离场航迹与限制使用空域的距离计算方法。散点状危险天气区域可看成多个凸多边形组成的危险天气区域，航线周围出现的散点状危险天气区域分别用SA1，SA2，…，SAn，…，SAN表示。首先，计算危险天气区域间的距离，假设SAm和SAn的顶点序列分别为om1，om2，…，omj，…，omJ和on1，on2，…，onk，…，onK，顺时针方向排列，J、K 表示危险天气区域SAm和SAn的顶点个数。要确定SAm和SAn间的距离，可先确定SAm的一点omj与SAn的距离，即omj与SAn所有边界点距离中的最短距离，omj与SAn间的距离为

确定omj与SAn的距离后，再依次确定SAm其他各点与SAn的距离，所有距离中最短的即为SAm和SAn间的距离，即

2）空域边界间的最短路径及距离

选取受影响航段首尾的两个航路点，设为ha，hb，两点连线组成线段H，SAn的顶点onk与线段H 的垂直交点为hnk，则顶点onk与H 的水平距离为

所有顶点中与H 距离最大的作为单个危险天气区域与H 的距离，即

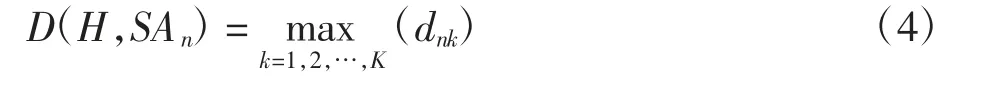
根据式（4）算出航线两侧每个危险区域与H 的距离。H 上侧记为正，下侧记为负，选出两侧距离最远的危险天气区域，作为起点vs和终点vt，与H 距离分别记为D1、D2，即

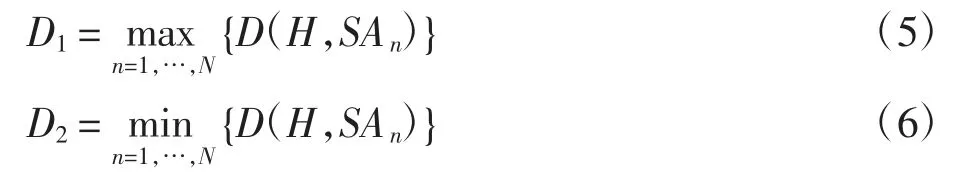
把危险天气区域作为节点vi依次连接起来形成网络，根据式（1）和式（2）计算相邻危险天气区域之间的距离，距离作为权。采用Floyd 算法求解vs到vt的最短路径。在H 两侧D1、D2距离的基础上向外扩展dsecurity（安全余度）作为假想空域边界。当存在散点状危险天气区域时，两侧空域边界间的最短路径D 为

两侧空域边界间的距离为

3）受影响部分的空域容量

当空域受散点状危险天气区域影响后，T 时刻受影响部分的容量为

其中：Ci为受影响部分的静态容量；D（T）为T 时刻两侧空域边界间的最短路径；L（T）为T 时刻两侧空域边界间的距离。

2.3 散点状危险天气下的进场空域利用率

散点状危险天气区域下的终端区进场空域利用率是给定时间段内的流量与容量之比，则t 时段内受散点状危险天气区域影响的终端区进场空域利用率，可表示为

其中：Fta表示t 时段内的进场流量；Cta表示t 时段内的平均进场容量。

T 时刻的进场容量C（aT）为

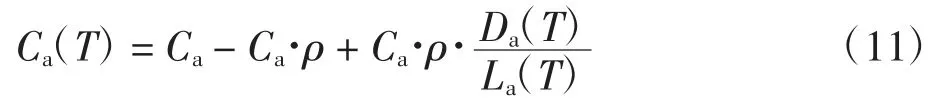
其中：Ca为终端区进场静态容量；ρ 为散点状危险天气区域所影响部分占进场容量的百分比；Da（T）和La（T）分别为散点状危险天气区域下T 时刻进场飞行受影响部分两侧空域边界间的最短路径与边界间的距离。而t 时段的进场平均小时容量为

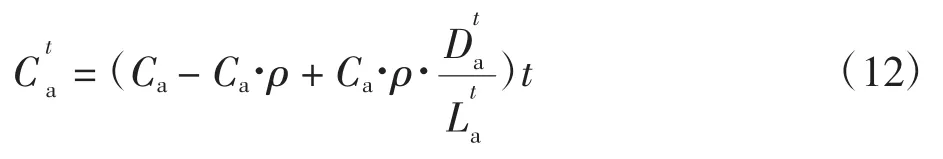
整理得，t 时段内散点状危险天气区域下的进场空域利用率模型为

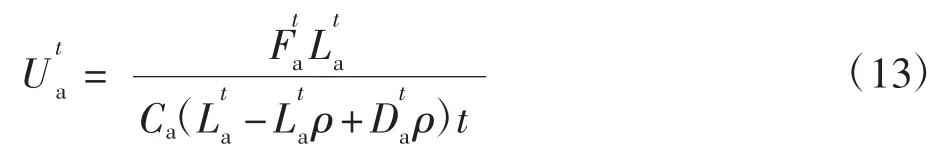
3 算例分析

选取国内某机场终端区，在其受散点状危险天气区域影响时，对其进场空域利用率进行评估，将机场与终端区作为整体考虑。研究时段为10：00—11：00，将其分为4 个时间片进行算例分析。已知终端区的进场容量为23 架/h，根据进场航线与散点状危险天气区域的相关数据，可得受影响航段和危险天气区域分布，如图3所示。由高峰时段各航线流量之比可得受影响部分所占进场容量的百分比ρ=0.4。

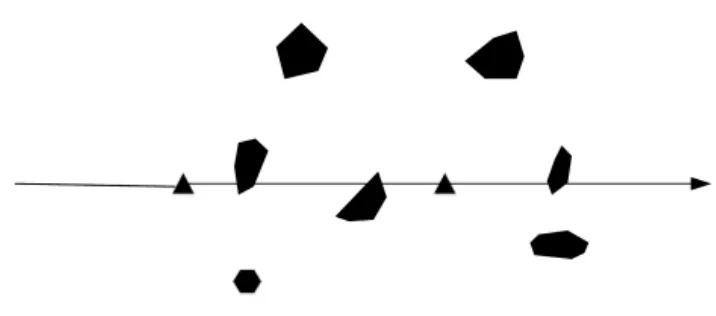
图3 散点状危险天气区域及受影响航段Fig.3 Scattered dangerous weather areas and affected flight segments

3.1 计算结果

将上述危险天气区域作为节点，根据式（5）和式（6），可得所研究时段初始时刻D1= 35.28 km、D2=24.33 km，确定起点vs和终点vt，依次连接形成网络，如图4所示。

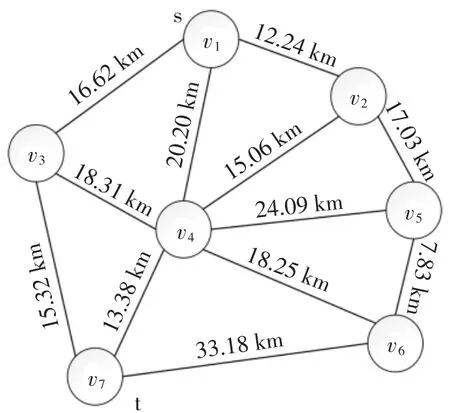
图4 散点状危险天气区域形成的网络图Fig.4 Network map formed by scattered hazardous weather area

图4中各节点间的距离为所研究时段初始时刻的距离，利用以上的距离，采用Floyd 算法求解vs到vt的最短路径，安全余度dsecurity=10 km，根据式（7）和式（8），可得初始时刻D（T）=51.94 km、L（T）=79.61 km。同理，在时段内每15 min 计算一次各时刻的D（T）与L（T），从而通过各时刻数据的平均值求得每个时间片内空域边界间的平均最短路径Dta和空域边界间的平均距离Lta，计算危险天气下的终端区进场空域利用率，还需要统计危险天气下各时间片的进场流量，通过式（13），可得散点状危险天气下各时间片内的进场空域利用率，如表1所示。

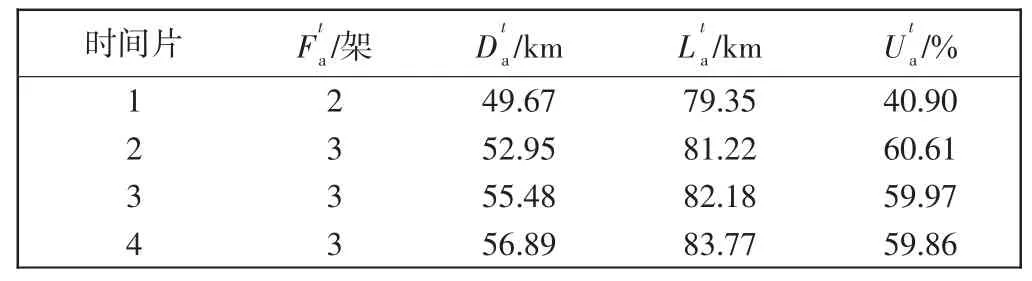
表1 散点状危险天气区域下进场空域利用率计算结果Tab.1 Calculation results of arrival airspace utilization rate in scattered dangerous weather areas

综合各时间片的进场空域利用率，可得散点状危险天气终端区1 h 的进场空域平均利用率为55.34%。

3.2 结果分析

从表1中可看出，随着时间的变化，Dta与Lta也在逐渐变化。随着时间的变化，散点状危险天气区域也在各自缓慢移动，同时自身也在发展或消散，与实际情况相符。选取正常天气下终端区高峰时段的小时进场空域利用率与之进行对比，进场流量为19 架，正常天气下Dta=0，通过模型可得同时段正常天气下进场利用率为82.61%。通过对比可知，当存在散点状危险天气区域时，空域利用率会明显下降。模型在终端区存在散点状危险天气区域时，能够真实地反映终端区空域的使用情况。

4 结语

基于散点状危险天气区域影响的空域利用率计算方法，利用最大流最小割的扩展定理分析散点状危险天气区域对航线容量的影响，并考虑时间、空间的限制，基于流容比建立进场空域利用率模型。为危险天气下的空域管理提供参考，在保证飞行安全的前提下，充分合理地利用有限空域资源，缓解空域拥挤、减少航班延误，从而在一定程度上提高空域的运行效率。