基于着陆轮迹测试的机场交通量平面分布模型

石鑫刚，蔡良才，王观虎

（空军工程大学航空工程学院，西安 710038）

目前，世界各国机场道面设计交通量分析都建立在交通量横向分布基础上[1-5]。Hosang[6]对美国9 个机场跑道、滑行道等部位的轮迹分布进行了测试，认为轮迹服从正态分布，并确定了轮迹正态分布的期望及标准差。国内一些轮迹分布测试结果也得到了正态分布的规律[7-9]。文献[10-13]针对民航机场流量大、测试飞机不好区分的特点，设计了一套轮迹横向分布测试系统，并在上海虹桥国际机场进行了现场测试。测试结果表明，轮迹偏移数据并不严格服从正态分布，而更符合极值分布或负偏态分布。

现有研究和规范仅局限于道面某一截面交通量的横向分布。事实上，道面各点交通量并不相同，交通量还存在纵向分布。由于受飞机滑跑偏移、航迹修正等因素影响，跑道纵向不同横断面的轮迹分布规律不断变化；同时受着陆接地点和起飞离地点分布的影响，会导致跑道纵向任意截面通行的总交通量次数不同。各国现行道面设计理论长期忽视纵向累积损伤分布的存在，导致不同设计方法在着陆运行次数的计算上存在分歧。美国联邦航空管理局（FAA, Federal Aviation Administration）认为可以忽略着陆交通量，而中国道面设计方法则坚持认为每着陆一次应按0.75次起飞计算，两种做法都存在一定的片面性。

为了研究道面各点的交通量，采用自研的激光测距系统对某型飞机17 个截面的着陆轮迹开展测试，并提出纵向通行因子，即某一横截面飞机通行次数与总通行次数的比值，用以反映由着陆接地点分布导致跑道纵向任意截面通行总交通量次数的不同。同时，联合横向分布规律拟合得到轮迹平面分布模型，实例验证了该模型可评价道面任意点的交通量。该模型提供了一种新的道面交通量平面分布测试方法，可为跑道平面尺寸设计和道面厚度分段设计提供交通量数据支撑。

1 机场跑道交通量分布特点

受公路交通量分布模型的影响，机场道面交通量分布模型被简单类比为公路交通量分布模型。事实上，公路与机场跑道在交通量分布上具有不同特点，公路交通量具有以下特点：①不考虑车辆短距离的加速运动，其在车道横断面的速度可认为是稳定的，即其交通量横向分布标准差是恒定的；②公路交通量虽然在车道横断面各点不同，但在车辆前进的纵向，车辆会通过纵向任意断面，可认为其交通量在纵向是恒定的；③当前公路交通量采用轮迹横向分布系数来计算各点的轴载作用次数，即假定轮迹在车道横断面是均匀分布的，是建立在一维空间基础上的点交通量。

机场道面交通量在跑道横断面上类似于公路，但两者存在以下较大差异：①由于飞机滑行过程中偏移的影响，交通量横向分布的标准差是不断变化的；②其交通量在跑道纵向也是不均匀分布的，由于飞机起飞起始位置、起飞滑跑距离不同，着陆接地点位置不同、着陆滑跑距离相差较大，以及飞机着陆后脱离跑道位置不同，机轮荷载在跑道纵向各点的作用次数也有差别，即交通量存在纵向分布。中国当前道面设计规范假定轮迹在通行宽度内服从均匀分布，为“点”的交通量模型。2008年FAA 提出的道面设计规范（AC150/5320-6E）[14]建立了基于累积损伤曲线的道面设计方法，其假设轮迹服从正态分布为“线”交通量模型。但实际机场交通量，尤其对于短距起降的飞机，不仅存在交通量的横向分布，且由于起飞离地点、着陆接地点及飞机侧滑性能的不同，交通量在跑道纵向上也是不断变化的，即跑道交通量具备平面分布特征，需建立“面”交通量模型。

2 机场跑道交通量测试系统

2.1 测试系统简介

激光测试系统主要由激光测距传感器、数据存储单元、可见激光校准装置、供电单元和支架等5 部分组成。分别采用深圳砝石激光雷达有限公司生产的FSA-ITS02 型激光测距传感器，深圳竞美科技有限公司生产的工业级串口数据记录仪，DANGER 牌激光笔，珩洁牌12 V/60 A 锂电池和铝合金支架。通过支架与设备连接部位可调整传感器高度，范围为75～100 cm，设备俯仰角的调节范围为-45°～45°。

2.2 测试概况与测点布设

测试地点选择在某军用机场，跑道尺寸为2 600 m×50 m，按照飞行计划对保障机型A（单一保障模式）开展轮迹分布测试。测试期间共对342 架次飞机的轮迹横向偏移进行记录，测试地点偏北风较多，故跑道南端为主起降方向。

将激光测距装置布设在跑道一侧的平地内，仪器到跑道中线的距离满足飞行安全要求，距离一般不小于60 m。现场布置过程中为避开驱鸟车通道和不便安装区域，设备到跑道中线的距离为72.2 ～93.3 m 不等，各测试设备布设距离如表1所示。

表1 各测试设备布设距离Tab.1 Layout distance of each test equipmentm

跑道纵向布设距离按照覆盖一半跑道，跑道端部着陆接地点附近加密布设，滑行区域适当稀疏布设的原则。根据测试机型的平均起飞距离和着陆点位置，将1 114 m 的测试区域分成2 个部分：①着陆滑跑区域，起始位置距离跑道端部183 m，共布设7 台仪器，覆盖飞机着陆接地较为集中的区域，间距为50 m 左右；②高速滑跑区域，共布设10 台仪器，为着陆高速滑跑区域，覆盖近半条跑道，间距为60 m 左右。具体设备布置如图1所示（测试坐标系以跑道中线为y轴，以跑道南端垂直于y 轴方向为x 轴，坐标原点O为跑道中心和跑道南端交点）。

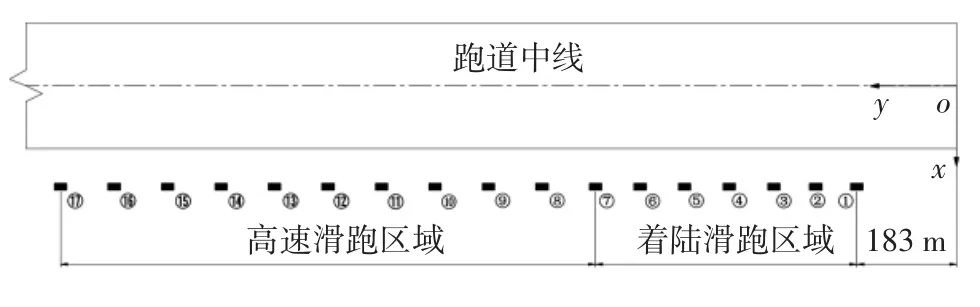
图1 现场设备布置图Fig.1 Field equipment layout

2.3 测式步骤

1）固定支架，并将激光测距测试单元安装在支架上，调节安装盘，使测试单元保持水平。

2）测试人员站在跑道中线测试单元正前方，调试板横向放置，1 名测试人员调整支架高度，使激光指示器的指示激光停留在调试板两侧参照点的位置，若激光测试单元有度数，且将调试板移开后度数消失，则测试单元架设高度确定。

3）沿跑道中线左右小范围移动调试板，同时左右调整支架使指示激光始终停留在调试板上参照点的位置，并观察激光传感器读数，当读数最小时，测量激光与跑道垂直，测试角度确定。

4）断电后安装内存卡，重新通电开始测试。

3 机场交通量分布模型

3.1 着陆轮迹横向分布

将17 组设备的着陆轮迹偏移横截面数据进行统计，并对所有截面数据开展K-S 正态性检验，3 号～17号P 值均大于0.05，服从正态分布，1 号～2 号截面由于数据量少，不足以统计其分布规律，计算结果如表2所示。采用3 号～17 号截面数据对着陆均值和标准差在跑道纵向的变化规律进行拟合，即

着陆均值和标准差拟合曲线如图2所示。由图2（a）可知，飞机着陆时，3 号～15 号各截面着陆均值先增大后减小，随着滑跑距离的增大，着陆均值逐渐减小，15 号～17 号各截面着陆均值近似保持不变，取其均值0.65 m 进行计算。由图2（b）可知，跑道端部标准差较大，随着滑跑距离的增大，标准差逐渐减少。分析拟合发现3 号～13 号截面轮迹分布标准差呈近似线性关系逐渐减小，此后截面的标准差近似保持不变，取13 号～17 号各截面标准差均值2.742 m 进行计算。

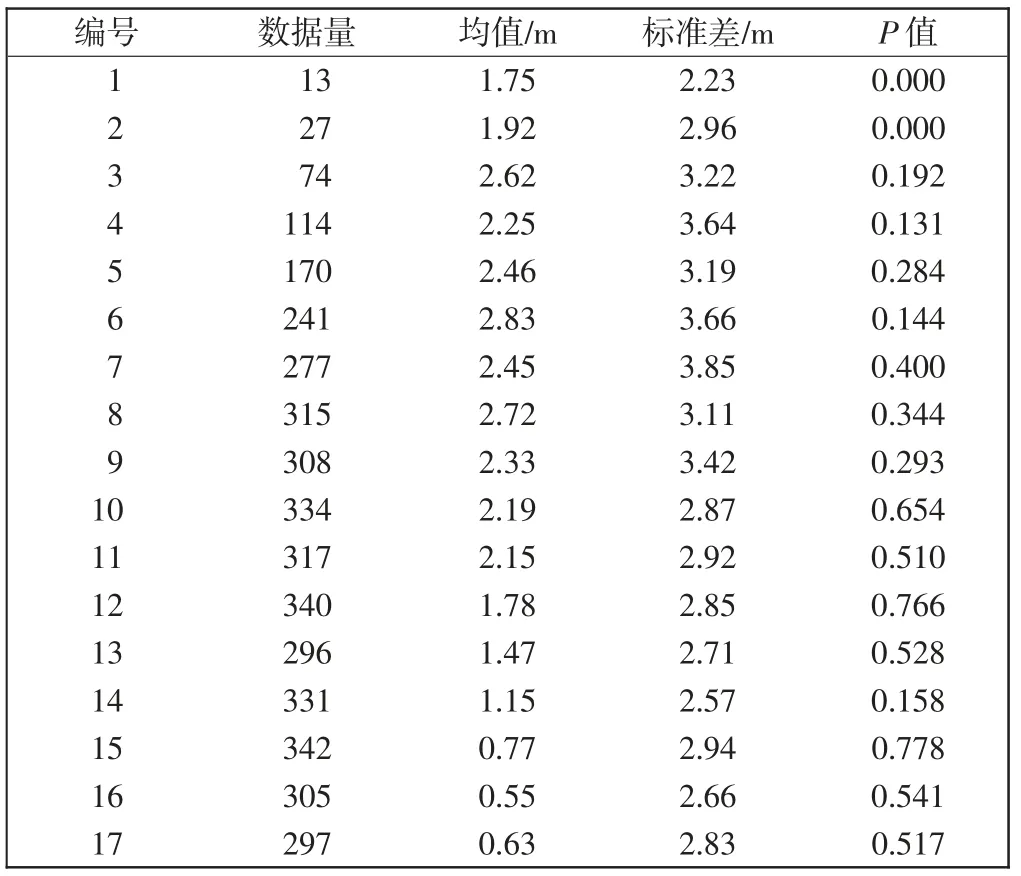
表2 着陆各横截面正态分布拟合数据Tab.2 Normal distribution fitting data of landing cross sections

图2 着陆均值和标准差在跑道纵向的变化规律Fig.2 Variation of mean and standard deviation along runway

上述着陆轮迹为靠近平地区主起落架机轮外侧轮迹，机轮中心点的轮迹分布均值需在外侧轮迹均值基础上加上半个机轮宽度（0.175 m），标准差保持不变，即靠近平地区主起落架机轮着陆轮迹正态分布表达式为

其中：x 为距跑道中线距离；y 为距跑道端部距离。

3.2 着陆交通量纵向分布

跑道长度要考虑最不利环境条件，对于大多数机型来说，一发失效状态下，飞机最大起飞或着陆质量下的滑跑距离，跑道长度都是足够的，会导致机场交通量不能布满整条跑道。定义纵向通行因子为

其中：Ny为飞机通过坐标处横断面的通行次数；N 为飞机总的通行次数。

根据跑道中部飞机着陆的轮胎痕迹可以看出飞机着陆点基本位于前9 台仪器测试范围内，除去偶尔仪器损坏的天数，1～9 号设备全部正常工作，各横截面着陆飞机通行数量统计，如表3所示。

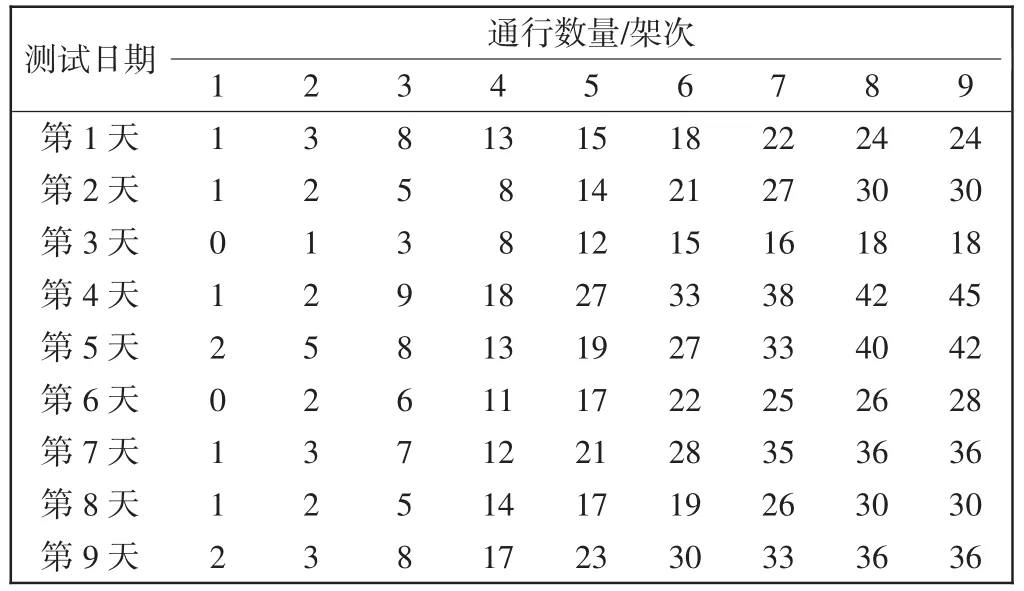
表3 各横截面着陆飞机通行数量统计表Tab.3 Landing aircraft statistics in each cross section

9 号仪器横截面位置以后，所有飞机均已着陆滑跑，根据纵向通行因子的概念可求得此后的纵向通行因子恒为1，一直持续到飞机驶离跑道的联络道处，通行因子根据驶离跑道的飞机数量而发生变化。值得说明的是，这里的纵向通行因子测试结果并不是各架次飞机起飞离地点和着陆接地点的原始坐标数据，不能采用假设检验的方法确定起飞离地点和着陆接地点的分布，仅是仪器截面所在跑道纵向坐标处的通行比例，因此，纵向通行因子沿跑道长度方向进行多项式拟合，结果如图3所示。

全跑道纵向通行因子可采用分段函数表示如下

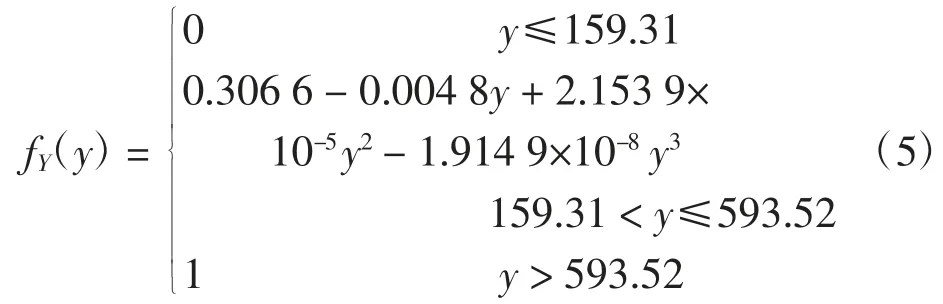
图3 着陆纵向通行因子拟合曲线Fig.3 Fitting curve of landing longitudinal passage factor

考虑到距离跑道南端380 m 处有1 条联络道，而另1 条联络道位于距离跑道北端600 m 处。飞机南端着陆时，全部飞机均从跑道端部驶离跑道，而飞机北端着陆时，从联络道与南端驶离跑道的数量比为2：8。因此，南端着陆的通行因子采用式（5），而跑道北端着陆纵向通行因子计算公式如下

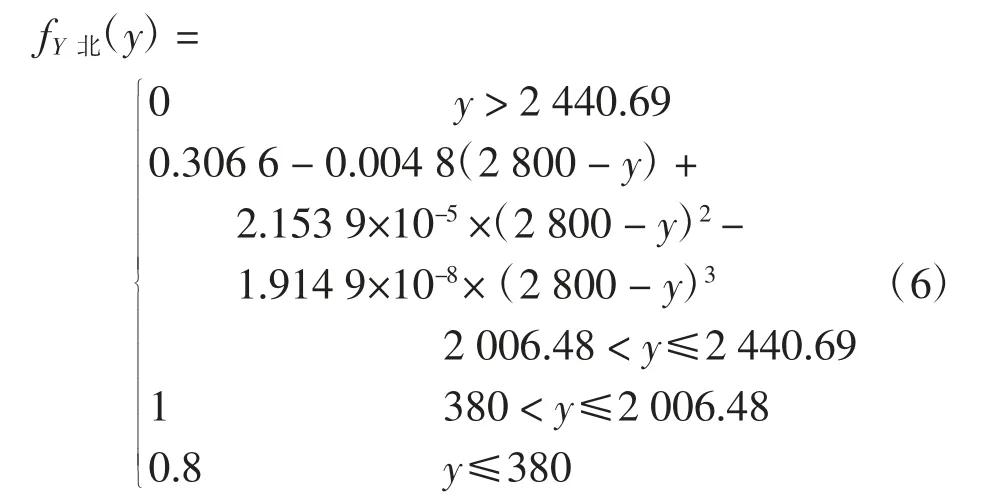
3.3 交通量平面分布

通过对机场交通量的横向和纵向分布规律进行统计分析，交通量横向正态分布反映的是该横断面上具体每一点的“流量”；纵向通行因子实际上是某一横断面总通行次数的概率表征，横向分布概率和纵向通行因子两者的联合分布即道面某一点的交通量概率。

假设设计寿命内机场所保障的飞行任务总量为N次，两端起降概率为a 和b，飞机着陆时道面各点的交通量计算公式如下

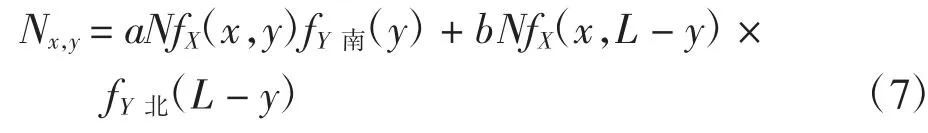
其中，L 为跑道长度。

式（7）为主起落架左轮中点的交通量模型，要计算主起落架轮迹总的覆盖作用次数，还需要叠加右轮轮迹中点交通量。不考虑飞机偏航和侧转角度的影响，则右轮迹中点交通量模型仅在左轮迹中点交通量模型基础上分布均值偏移一个主起落架间距（4.34 m），左右轮迹中心交通量的叠加即为主起落架轮迹总的覆盖作用次数。

4 实例分析

4.1 应用实例

假设该机场保障机型在设计寿命范围内的起降架次为100 000，跑道长度2 600 m，南北两端起降架次比例为7：3。某型飞机从南端着陆时，联络道位于600 m处，几乎飞机全部从跑道北端驶离跑道，而飞机北端着陆时，从联络道（纵向坐标为380 m）与南端驶离跑道的数量比为2：8。由轮迹分布测试统计规律和交通量平面分布模型，可得到着陆状态下主起落架机轮覆盖作用次数，如图4所示。

图4 着陆交通量分布曲面Fig.4 Landing traffic volume distribution surface

由图4中交通量分布可知，交通量的纵向分布明显，尤其对于跑道纵坐标380 m 处，由于存在部分飞机从联络道处驶离跑道，交通量在此处会发生突变。由上述模型可以计算着陆时道面每点的覆盖作用次数，也可以求得着陆最大覆盖作用次数为21 275 次。若按照规范仅计算该机型轮迹横向分布，均值为0.02 m，标准差为2.83 m，不考虑交通量的纵向分布，则道面交通量如图5所示。

由图5可看出，仅考虑横向分布得到的交通量曲线模型实际是交通量曲面模型的1 个截面的特殊情况，并未考虑飞机的着陆点位、滑行轨迹及各横断面纵向交通量的变化。

4.2 影响因素分析

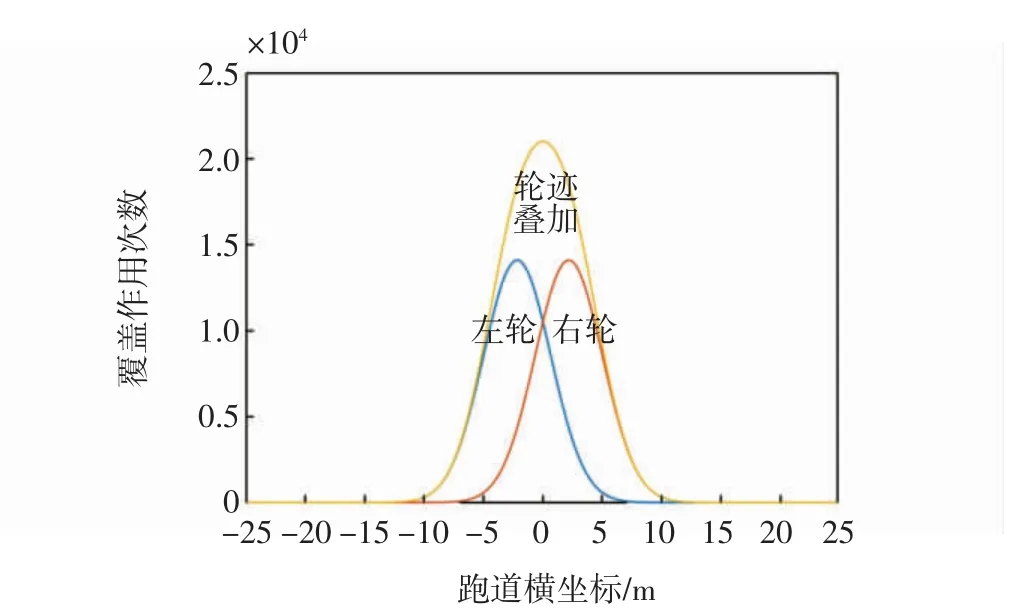
图5 交通量横向分布曲线Fig.5 Horizontal traffic volume distribution curve

为了研究交通量平面分布模型各影响因素的敏感性，分析了跑道长度、两端起降概率、轮迹分布标准差对交通量分布曲面的影响。

4.2.1 跑道长度

图6给出了跑道长度为3 000 m 和2 200 m 着陆交通量曲面侧视图，如图6所示。

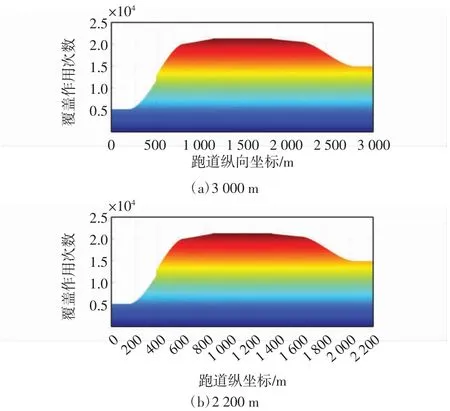
图6 不同跑道长度下着陆交通量分布曲面侧视图Fig.6 Side view of landing traffic volume distribution under different runway lengths

由图6及图4（b）可知，跑道长度为3000m，2600 m，2 200 m 时，着陆最大覆盖作用次数出现在跑道中部范围内，均为21 275 次。不同方向起降的飞机，轮迹在跑道中部发生叠加，随着跑道长度增大，跑道中部纵向轮迹叠加效应范围越大。

4.2.2 两端起降概率

保持实例中的其他参数不变，图7分别仿真计算了起降概率为1：1 和仅一端起降两种概率下着陆交通量分布曲面，如图7所示。

由图7及图4（a）可知，由于跑道中部通行因子均为1，轮迹最大覆盖作用次数保持不变。但一端起降状态下，飞机沿既定轨道滑行，除着陆点附近和飞机滑离跑道的位置外，其他横截面均达到最大轮迹覆盖作用次数。两端起降概率相等时，轮迹覆盖作用次数分布较为平均，最大轮迹覆盖作用范围最小，有利于荷载作用的均匀分布，延长道面的使用寿命。

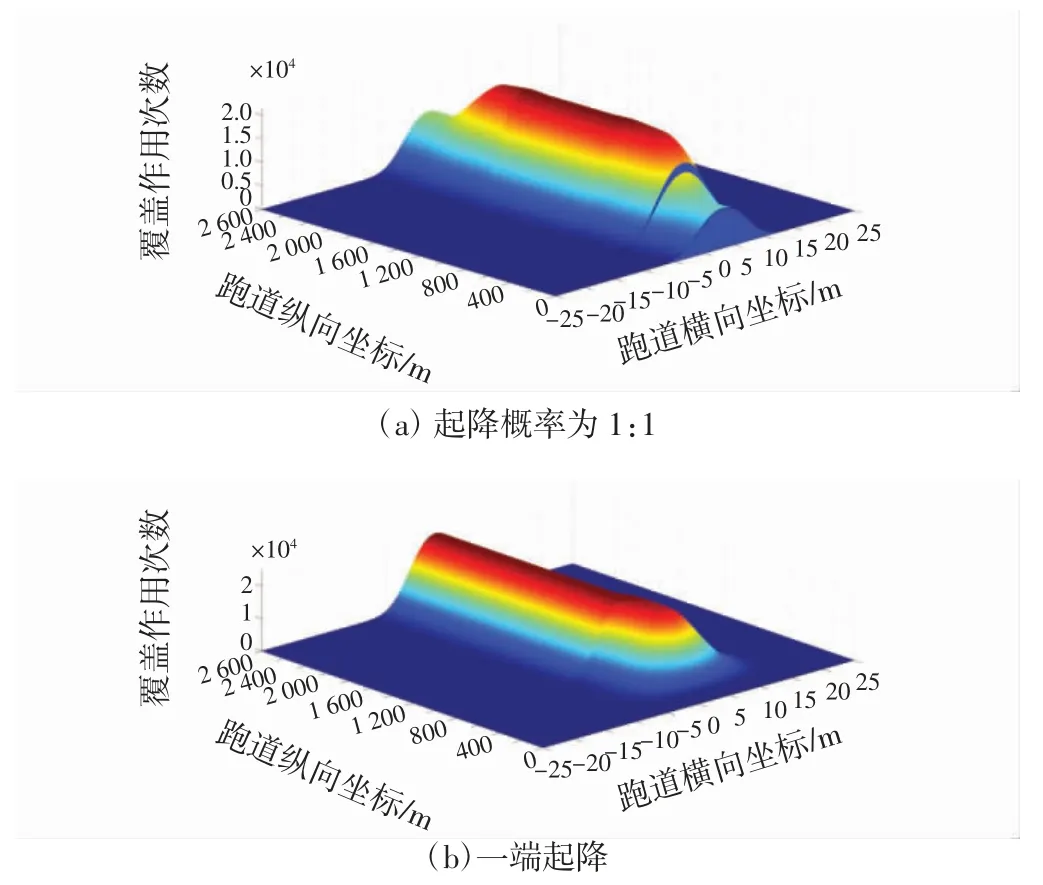
图7 不同起降概率下着陆交通量曲面图Fig.7 Landing traffic volume under different landing probabilities

4.2.3 轮迹分布标准差

跑道宽度、气象条件、飞行员的驾驶技术等因素，都对轮迹的横向分布产生一定的影响，即影响各横截面的均值和标准差，但由于测试条件限制，并未开展该方面的统计和分析工作。在此，忽略这些因素对轮迹分布均值的影响，仅研究不同轮迹分布标准差状态下交通量的变化规律。

由式（2）可知，当标准差增大0.2 m 时，得到的最大轮迹覆盖作用次数为20 611，比原曲面最大值减小3.12%；标准差减小0.2 m 时，最大轮迹覆盖作用次数为21 803，比实际测试的交通量分布曲面最大值增大2.48%。轮迹分布标准差越小，轮迹横向叠加效应越明显，道面交通量分布越集中。

5 结语

通过飞机轮迹平面分布测试系统对某型飞机的着陆轮迹开展测试，得到主要结论如下。

1）采用激光测试技术对着陆状态下的轮迹分布开展现场测试，统计分析了轮迹横向分布规律。飞机着陆时，随着滑跑距离的增大，轮迹偏移均值先增大后减小，减小至0.65 m 后保持不变；跑道端部标准差较大，而后逐渐减少至2.742 m 保持不变。

2）提出纵向通行因子的概念，研究跑道交通量的纵向分布规律，在测试统计分析的基础上建立了机场交通量平面分布模型，并通过实例验证了交通量平面分布模型可评价道面各点的覆盖作用次数。现行规范交通量计算方法得到的交通量曲线实际是交通量曲面模型1 个截面的特殊情况。

3）分析了跑道长度、两端起降概率、轮迹分布标准差对交通量平面分布的影响。跑道长度主要影响跑道纵向中部范围交通量的叠加效应，对交通量最大值影响相对较小；两端起降概率影响轮迹分布的均匀性；跑道宽度、气象条件、飞行员驾驶技术等因素会导致交通量横向分布的变化，轮迹分布标准差越小，轮迹横向叠加效应越明显，道面交通量分布越集中。

机场交通量模型由横向分布曲线发展为横纵向分布曲面，结合飞机的运行特性，可以为跑道平面尺寸设计和道面厚度分段设计提供交通量依据。