基于FMM-PM方法的宇宙N体模拟在GPU上的实现和优化

扶月月，王武，王乔

1.中国科学院计算机网络信息中心，北京 100190

2.中国科学院大学，北京 100049

3.中国科学院国家天文台，北京 100101

引言

N体问题计算相互作用的N个粒子的相互作用和运动，是高性能计算中具有代表性和挑战性的问题之一，在天体物理、分子动力学、磁流体动力学等领域具有广泛的应用。模拟N体问题的数值方法包括直接法（Particle-Particle，PP）、树方法（Tree Method）和粒子网格方法(Particle Mesh，PM)等，其中树方法有BH 方法(Barnes-Hut)[1]和快速多极子方法 (Fast Multipole Method，FMM)[2]。PP方法的复杂度为O(N2)，其中N为粒子规模，这限制了模拟问题的规模；BH 方法的复杂度为O(NlogN)，且计算精度可控；FMM的复杂度为O(N)，兼具精度和速度优势，被IEEE 计算机协会和美国计算物理学会列为20世纪十大算法之一[3]；基于快傅里叶变换（Fast Fourier Transform，FFT）的PM 方法[4]复杂度为O(NlogN)，虽然计算速度较快，但计算短程力时不精确，只适用于长程力计算。为了弥补PM方法计算精度不足的缺点，PM 混合算法应运而生，PM 方法结合直接法和树方法的混合算法（P3M[5]、TreePM[6]）应用广泛。

随着高性能计算技术的发展，以及天文学和分子动力学等领域对大规模计算需求的增长，仅从算法上降低计算复杂度或者增加CPU 核数量并不足以满足领域科学家的计算需求。采用硬件加速来加快计算速度，从而扩大计算规模也是较为可行的途径。GPU的最新发展已经能够以低廉的成本提供高性能的通用计算，基于CPU+GPU的并行异构架构也已成为当今大型超级计算机的主流体系结构之一。例如，2019年11月全球TOP500 排行榜前10名的超级计算机中，有5台使用了CPU+GPU的异构体系结构。

近些年N体问题成为了GPU 上的热点应用之一，国际上有不少针对各个算法使用GPU 来加速N体模拟的研究，很多显著的研究成果都是对PP 方法的N体模拟软件进行GPU 优化加速[7-9]，基于BH方法和FMM 方法在大规模GPU 集群上的性能提升的研究成果也不少[10-12]，但是利用CPU+GPU 异构平台对PM 混合算法进行优化加速的研究并不多，目前还没有在GPU 集群上实现FMM-PM 耦合算法的N体模拟。本文采用FMM-PM 耦合的方法实现N体问题的模拟，既可兼顾计算速度和精度，又能重叠短程力的计算与长程力的通信，因此较适合大规模并行。我们的工作为今后对多体问题和异构体系结构的研究工作奠定了坚实的基础。

宇宙模拟软件PHoToNs是针对宇宙暗物质大尺度结构设计的N体模拟软件[13]，其第二个版本改进了引力的计算算法，采用了FMM-PM 耦合算法实现，其中FMM的核心函数在GPU 上实现，FMM 中计算量较小的算子、PM函数和通信函数在CPU上实现，本文给出了该软件在CPU+GPU 架构上的实现过程和性能优化技术。第1 节介绍FMM-PM 耦合算法的基本原理和计算流程，第2 节介绍FMM 在GPU 上的实现策略，第3节介绍FMM 在GPU 上的三种性能优化方法，第4 节给出测试结果。

1 FMM-PM 算法原理

1.1 快速多极子方法

天文N体问题主要计算引力场中的N个粒子（星体、星系或暗物质都可以抽象为粒子）的相互作用和运动，粒子所受作用力可表示为：

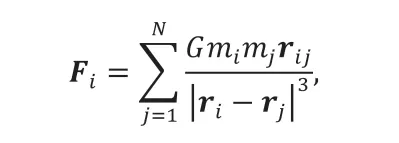
其中i= 1,2,...,N，G是引力常量，mi和mj是粒子i和j的质量，rij=xi-xj为粒子i到j的位移矢量。采用该公式直接计算每对粒子之间的相互作用，其精度较高且易于并行实现，然而需要每次重复计算各个时间步，这个过程的时间复杂度为O(N2)，模拟问题的粒子规模大大受限。

FMM 将粒子的相互作用分为远场和近场作用，远场作用通过近似方法来计算，在近场作用的计算过程中，通过层次划分和位势函数的多极子展开计算各点位势，然后将位势转换为各点所受的力。位势和引力满足：

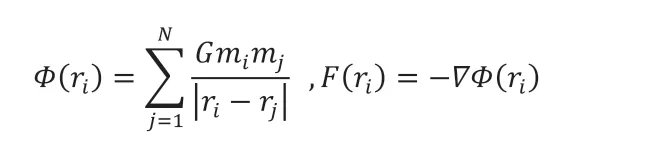
其中i= 1,2,...N,mi,ri,F(ri)分别为粒子的质量、位置、位势和作用力。虽然近场部分使用直接法，但由于短程力作用范围有限，近场作用的粒子对数量远小于远场作用，所以FMM 整体复杂度仍为O(N)。

FMM的核心思想是：首先将空间进行多层组划分，然后通过核函数多极子展开，将粒子的位势聚集到所在盒子的中心，逐层向上递归计算各层盒子的展开系数，最后把粒子间的远场相互作用转换为盒子中心之间的相互作用，逐层向下递归到所有叶盒子。FMM 树结构递归过程的示意图见图1，向上箭头表示M2M 逐层聚集，向下箭头表示逐层发散，水平虚线表示次相邻转移。

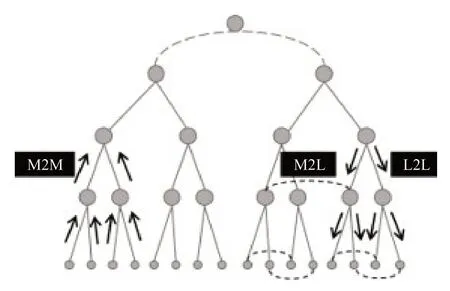
图1 FMM 树结构算法示意图Fig.1 FMM tree structure algorithm diagram

FMM 逐层递推过程包括以下七个基本步骤：

(1)空间多层盒子划分，自下而上构造树；

(2)计算每个叶盒子的多极子展开系数和粒子与叶盒子的相互作用（P2M)，然后逐层上聚到父盒子中心（M2M）；

(3)计算次相邻盒子的相互作用，即级数展开系数的转换（M2L）；

(4)逐层向下计算各盒子的局部展开系数以及父盒子对子盒子的作用（L2L）；

(5)采用直接法计算每个叶盒子和相邻盒子里所有粒子的近相互作用（Fnear-field）；

(6)计算所有粒子的位势和受到的长程力相互作用（Ffar-field）；

(7)计算所有粒子的加速度，基于蛙跳格式更新下一时刻的速度和位置。

1.2 粒子网格方法

粒子网格（Particle Mesh，PM）方法基于谱空间的位势场泊松方程求解粒子系统的引力，它应用于具有周期边界的N体模拟。PM 方法根据粒子信息得到均匀网格上的密度分布函数，求解出网格点的位势，然后根据粒子所处的网格单元位置，通过差分和插值得到每个粒子所在点的位势和所受的力。PM 方法的基本步骤如下：

(1)构造密度分布：基于粒子的分布情况计算构造均匀网格，以及格点的密度分布函数；

(3)计算作用力：通过有限差分和插值方法从格点的位势得到粒子所受的力；

(4)计算加速度：根据粒子质量，将每个粒子的受力转换为加速度；

(5)速度和位置更新：基于时间步进积分（可采用蛙跳格式、龙格-库塔格式等）计算各粒子下一时刻的速度和位置。

与PP 方法相比，PM 方法的网格点数量与粒子数相当或者更少，而且基于规则网格的密度场分布通过谱空间的FFT 求解各点的引力势，仅涉及到两次FFT，其复杂度为O(NglogNg)，其中Ng为离散网格点数，所以PM 计算速度较快，但是如果粒子间的距离较小时，该方法算出的粒子受力计算精确不能满足要求，因此PM 只适合计算粒子的长程力相互作用。

1.3 FMM-PM 耦合方法

耦合方法把引力势拆分成长程和短程部分，其中长程部分通过谱空间位势的傅立叶变换算出，短程部分通过位形空间泊松方程求解得到，计算公式如下：

俗话说：“爱子爱在心里。”然而，他爱子是爱在脸上的。有一次，我应邀在其老家作客，吃饭时，大人还没有动筷子，他的大儿子却大口大口地先吃起来，还说：“这是我要吃的，你们不能吃！”一点规矩都没有。然郑君只是轻描淡写地说一句：“老大！客人在，你收敛些好吗！”饭后，我和郑君正在品茶谈天，突然，有一孩子哭着来告状，说是他额头上的乌青块是郑君的大儿子用砖头砸的。郑君连句安慰他的话都没有，却反问那个孩子：“他为什么砸你，而不砸别人呢?”这无疑是在默认、纵容其子的错误行为。

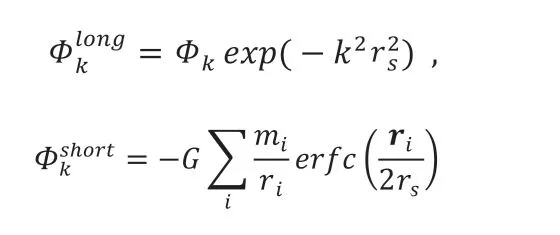
Hockney 等人在1974年提出P3M[5]方法，采用PP 方法计算短程力，它早期用于等离子体模拟，后来应用于宇宙模拟；Xu G 等在1995年提出TreePM[6]方法，采用树方法计算短程力，TreePM 方法带来计算性能的显著提升，在天体物理和分子动力学中得到广泛应用。目前国际主流的宇宙N体模拟软件就是采用TreePM 方法（如GADGET[14]）。

天文N体模拟软件PHoToNs-2.0 采用FMM-PM耦合算法，长程力采用基于FFT的PM 方法求得，短程力通过FMM 计算。基于FFT的PM 方法虽然速度更快，但受限于精度，只适用于计算长程力，而且会带来全局通信。FMM 不仅具有近似线性的复杂度和较高的精度，而且适合并行。其中近场相互作用是计算密集型的，可有效利用高性能异构平台的加速器件（如GPU、MIC 等）。采用FMM-PM 耦合算法来实现N体问题的大规模并行，既兼顾了计算速度和精度，又重叠了短程力的计算与长程力的通信。

图2为FMM-PM 耦合算法示意图，虚线内为FMM 计算区域，其中粒子间的短程力相互作用（P2P）占FMM 计算时间的90%以上，适合在加速卡上实现；虚线外的区域基于三维FFT的PM 方法计算长程力，占整体运行时间的比例约1%，因此不需要采用GPU 加速，可在CPU 端调用FFT 函数库(如FFTW、P3DFFT 等)实现，PHoToNs-2.0 采用二维区域分解的三维并行FFT 函数库2decomp-FFT[15]。

图2 FMM-PM 耦合算法示意图Fig.2 FMM-PM algorithm diagram

2 FMM 在GPU 上的实现

FMM的本地和非本地短程作用（P2P）的计算时间占FMM-PM 运行时间的比例最高（对于大规模问题，通常在90%以上），考虑到P2P 算子是计算密集型和数据密集型，可采用GPU 进行加速。FMM其它计算（构造树，盒子-粒子作用等）是访存、传输密集型函数，计算量相对较小。核心函数P2P_kernel是计算短程力的主要函数，其作用是通过粒子的位置、质量等信息算出粒子的受力和加速度。P2P_kernel 在GPU 上实现的过程如下：

(1)CPU 获取任务队列，做数据传输准备，开辟显存空间；

(2)CPU 把需要计算的粒子信息传输到显存；

(3)GPU 上计算粒子的短程力相互作用；

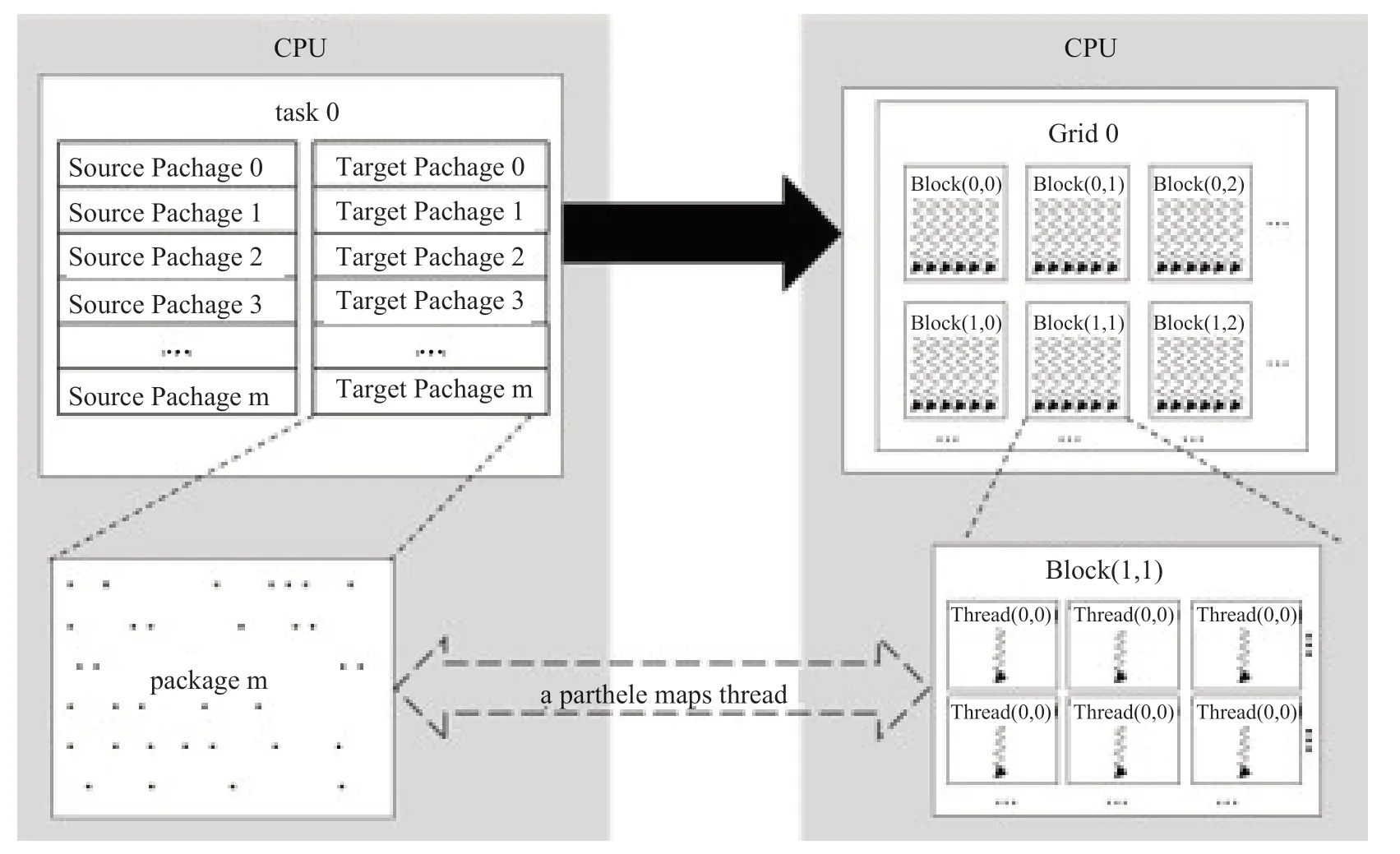
图3 计算任务（包）与GPU 线程映射关系示意图Fig.3 Mapping relationship diagram between computing tasks (packages) and GPU threads

(5) CPU 端更新粒子信息。

在具体实现，把按顺序存放的粒子信息以及其邻居粒子分批存入CPU 中开辟的缓冲池中，之后一起存入GPU 显存中保证完整性，而且使GPU有序访问显存，提高存取效率。如图3所示，根据CUDA 编程模型，一个线程映射一个粒子信息，充分发挥GPU 计算线程较多的优势。

3 FMM 在GPU 上的性能优化

3.1 核心函数的参数优化

在FMM 中MaxPackage 参数至关重要，它表示树结构最细层粒子包中的粒子数上限，其大小与任务量和数据传输开销有关。随着MaxPackage 增大，虽然单次执行核函数的任务量增大，但总任务次数减小，总数据传输开销也随之减小。反之，MaxPackage 减小，总数据传输开销增大。短程力数据传输的复杂度可表示为：

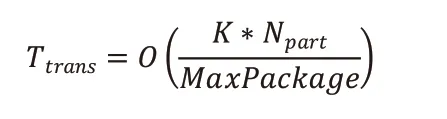
其中Npart表示每个进程的粒子数，常数K表示每个盒子的近场相邻盒子数，包括该盒子本身，取值与截断半径和判断准则有关。

MaxPackage 参数分别与数据传输量和数据传输时间关系如图4和图5所示。

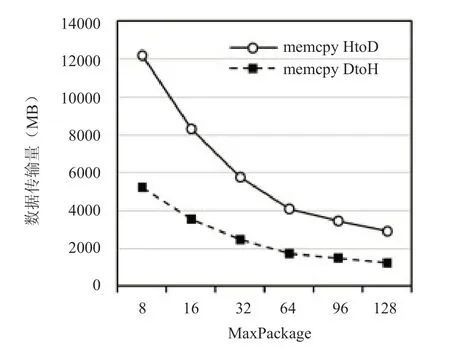
图4 MaxPackage与数据传输量的关系Fig.4 The relationship between MaxPackage and the amount of data transmitte

图5 MaxPackage与数据传输时间的关系Fig.5 The relationship between MaxPackage and the Data transfer time

图6为使用nvprof 工具分析内存拷贝时间与核心函数p2p_kenel的执行时间分别占P2P 计算总执行时间的比重。其中，memcpyHtoD和memcpyDtoH分别表示从主机端到设备端的内存拷贝和从设备端到主机端的内存拷贝。可见，在多GPU 系统中，数据传输时间占总P2P 短程作用力的计算总时间的90%以上。虽然短程力计算量与MaxPackage 成正比，但测试表明在GPU 上传输比计算更耗时间，即P2P计算复杂度可表示为：

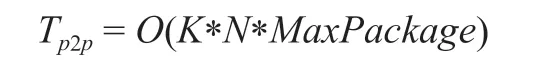
因此，在GPU 上通过增大MaxPackage 参数，可以减少数据传输开销，进一步优化P2P 短程作用力的计算和传输总时间。

3.2 页锁定内存优化和CUDA 流优化

对CUDA 架构而言，传统的内存拷贝方式是由操作系统API malloc( )在主机上分配的同时用cudaMalloc( )分配设备内存，这种内存，方式称为可分页内存（page-able memory）。可分页内存的内存拷贝非常耗时，为了加速内存拷贝，CUDA 提供了页锁定内存（page-lock memory 或 pinned memory）机制来而分配主机内存，即采用API cudaHostAlloc( )分配主机内存。使用页锁定内存方式分配的主机内存会常驻物理内存中，操作系统将不会对该内存进行分页和交换到磁盘上，这块内存不会被破坏或者重新定位，所以操作系统能够安全地使某个应用程序访问该内存的物理地址。CPU与GPU 内存交互方式如图7所示，CPU和GPU之间的总线是PCIe，是双向传输的，CPU和GPU之间的数据拷贝使用DMA 机制来实现。

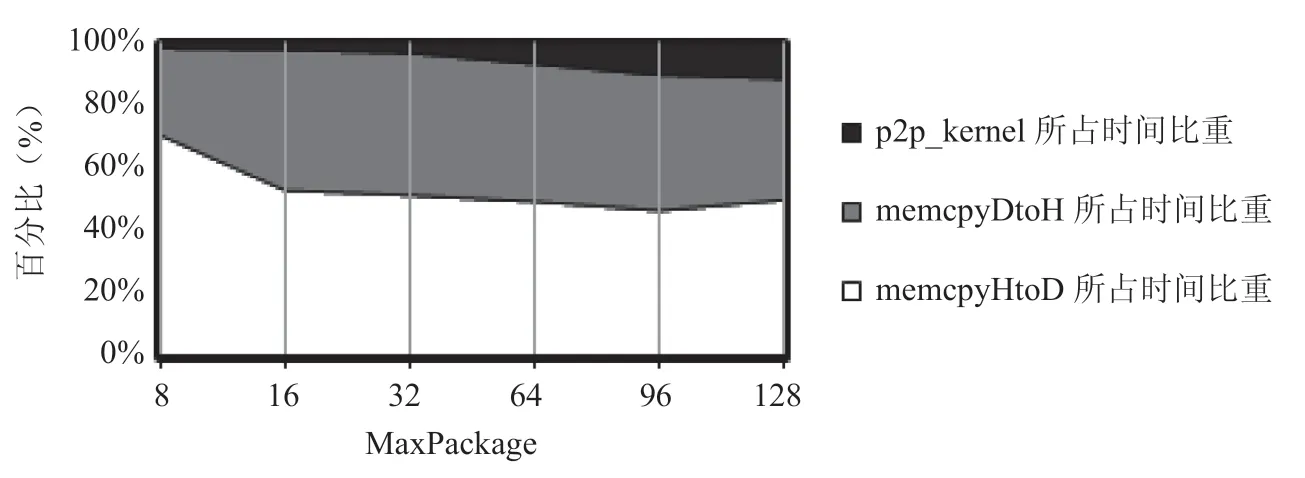
图6 memcpyHtoD、memcpyHtoD 以及p2p_kernel所占的时间比重Fig.6 Time proportion of memcpyHtoD,memcpyHtoD and p2p_kernel

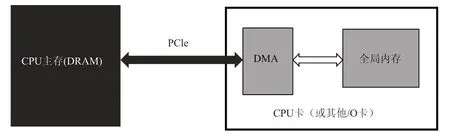
图7 CPU与GPU之间的内存交互示意图Fig.7 Memory interaction diagram between CPU and GPU

在进行内存复制操作时，若采用传统的可分页方式，CUDA 驱动程序仍会通过DRAM 把数据传给GPU，这样复制操作会执行两遍：先从可分页内存复制一块到临时的页锁定内存，再从这个临时的页锁定内存复制到GPU 上。当从可分页内存中执行复制时，复制速度将受限制于PCIE 总线的传输速度和系统前段速度相对较低的一方。使用了页锁定内存时，GPU可以直接确定内存的物理地址，从而能够使用DMA 技术在GPU和CPU之间拷贝数据。显然，使用页锁定内存大大减少了CPU与GPU之间数据传输时间，最大化内存吞吐量，提高内存带宽。

CUDA 流包括一系列异步的CUDA 操作（主机与设备间的数据传输，内核启动以及由主机发起但由设备处理的一些命令）。CUDA 流按照主机程序确定的顺序在设备端执行，相对于主机是异步的。可以使用CUDA的API 来确保一个异步操作在运行结果被使用前完成。在同一个CUDA 流中的操作有严格的执行顺序，而在不同CUDA 流中的操作在执行顺序上不受限制。

使用多个CUDA 流同时启动多个kernel可实现网格级并发，因为所有排队的操作都是异步的，所以在主机与设备系统中可重叠执行部分操作。在同一时间内将流中排队的操作与其他并发操作一起执行，可以隐藏部分操作的时间开销，使设备利用率最大化。图8为使用2个CUDA流的性能提升示意图，可以看出，在一个流中设备端的计算kernel与另一个流中设备到主机的数据传输是重叠的。

3.3 混合精度和快速数学库优化

单精度和双精度浮点运算在通信和计算上的性能差异是不可忽略的。在我们的程序中，使用双精度数值能够使程序运行总时间增加近一倍(这个结果取决于程序是计算密集型还是I/O 密集型)，在设备端进行数据通信的时间也是使用单精度的两倍，这是由于传输数组的字节长度相差两倍。随着全局内存输入/输出数量和每条指令执行的位操作数量的增加，设备上的计算时间也会增加。为了最大化指令吞吐率，我们使用单精度数(float)常量、变量和单精度计算函数，仅在有必要的时候使用双精度运算。

内部函数__fdividef与除法运算相比，在执行浮点除法时速度更快但数值精度相对较低。用功能上等价的__fdividef 来替换除法操作，可以加速程序运行。另外，快速数学库（Fast Math Library）可以将核函数中使用的单精度计算函数替换为CUDA 内部实现的高速版本。我们对核函数中单精度浮点类型的超越函数（erfc）调用快速数学库，程序性能大大提升。

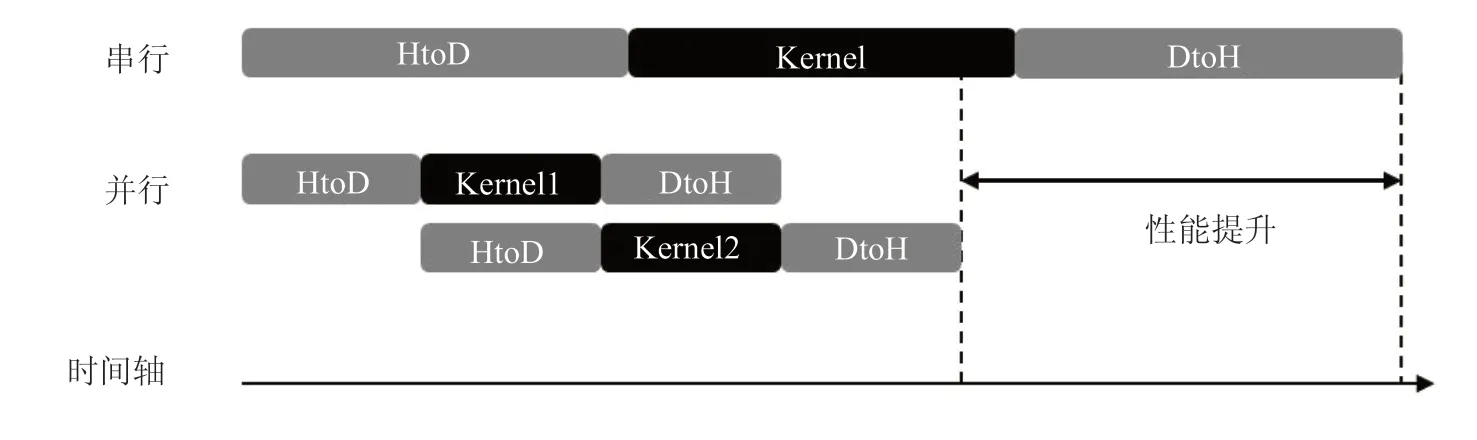
图8 使用2个流的CUDA 操作性能提升示意图Fig.8 Performance improvement diagram of CUDA operation using 2 streams

4 数值结果

在浪潮NF5280M5 服务器上进行测试。系统环境配置：2个Intel Xeon Gold 6148（20 核心*2），主频为2.4GHz，12个内存条 DDR4 2400 DDR4 （32GB *12）；4 张NVIDIA TITAN V GPU卡，显存容量12GBS，CUDA 版本为9.1，采用Intel 编译器和“-O3”优化。

对优化后的CUDA 版本程序进行加速效果测试，粒子规模为两百万（1283），使用4个进程，在浪潮服务器上单个时间步的模拟。图9为不同MaxPackage 三个实现版本程序的数据传输时间对比。其中，版本1是未进行优化的CUDA 程序，版本2是表示使用页锁定内存和CUDA 流优化后的程序，版本3为使用混合精度调用快速数学库优化的程序。可见，MaxPackage 越大，数据传输越快，系统性能越好。

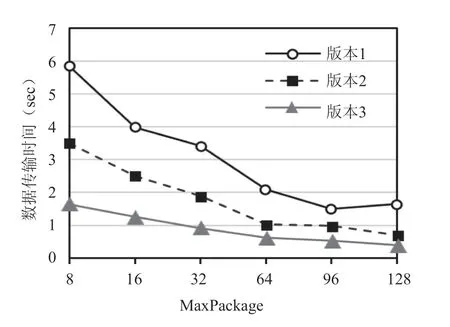
图9 不同MaxPackage 三个优化版本的数据传输时间对比Fig.9 Data transfer time comparison between three optimized versions of different MaxPackage

图10为PHoToNs-2.0的纯MPI程序和三个CUDA 实现版本程序的短程力计算函数P2P 运行时间的对比，图11为三个CUDA 实现版本采用不同MaxPackage值时P2P的加速倍数。可以看出，当MaxPackage为128 时，核心函数P2P 执行时间从475.9s 降到了1.16秒，加速了410.3倍。

图10 纯MPI 程序与三个CUDA 实现版本程序的P2P 函数执行时间对比Fig.10 Comparison of P2P function execution time between pure MPI program and three CUDA implementation version programs

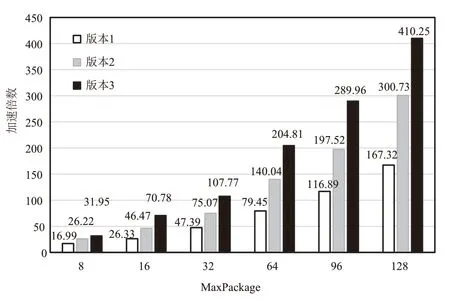
图11 不同MaxPackage 三个CUDA 实现版本程序的P2P 函数加速倍数Fig.11 P2P acceleration multiples of three CUDA versions of different MaxPackages

5 结论与展望

本文在CPU+GPU 混合异构平台的，对基于快速多极子方法和粒子网格方法的N体模拟软件PHoToN-2.0 进行CUDA 实现和性能优化，包括优化粒子包的参数以减少数据传输开销、使用页锁定内存提高内存带宽和最大化内存吞吐量、使用CUDA流优化最大化设备利用率、采用混合精度优化最大化指令吞吐率、有效利用快速数学库等手段。最终，FMM-PM 耗时90%以上的核心函数P2P 在在Titan V的GPU 平台上采用4 张GPU 卡的计算速度相对采用4个Intel Xeon CPU 核提高了约410倍。这些优化方法为在大规模GPU 异构平台上进一步优化和超大规模天文N体模拟奠定了基础。

利益冲突声明

所有作者声明不存在利益冲突关系。