含弹性应变能的各向异性相场模型的指数时间差分方法

王姗姗，张鉴

1. 中国科学院计算机网络信息中心，北京 100190

2. 中国科学院大学，北京 100049

引言

相场法是近年来出现的一种强有力的计算方法，用于建模和预测材料的中尺度形态和微观结构演变[1]。相场法使用一组守恒和非守恒的在区域内连续的场变量来描述微观结构。经典的相场方程——Allen-Cahn 方程[2]和Cahn-Hilliard 方程[3]，描述了场变量在空间和时间上的改变。微观结构的繁杂演化可以被相场法有效的描述，而无需明确跟踪界面的位置。相场法已成为模拟中尺度微观结构演化的一种重要而通用的方法。

对于经典的Allen-Cahn方程和Cahn-Hilliard方程，已有基于有限差分格式的时间推进求解方案。这些求解方案普遍存在着缺陷：很难设计高阶的求解格式、时间步长无法取到令人满意的长度等。本文所使用的紧致指数时间差分方法（compact Exponential Time Difference, cETD）[4-5]，对于经典的相场方程的高阶导数项，采用积分因子法进行准确积分，而对于它们的非线性项，又与经典的积分因子法不同，紧致指数时间差分方法对方程的非线性部分利用多步逼近、龙格库塔、预估校正等方法设计了高阶的求解格式，并且利用算子分裂格式增强了整体的稳定性。

微观结构演化的动力是系统的总能量下降，系统的总自由能包括化学自由能、界面能、弹性应变能、电磁能、静电能等。其中，界面能各向异性和弹性应变能是材料产生各向异性的主要因素。界面能是微结构的界面上由于组成和结构的不均匀产生的额外的能量，由于固体的晶体性质，界面能通常是各向异性的，界面能各向异性的程度可以对粒子的生长形态和平衡形状产生重大影响，在相场方程中，界面能各向异性表现为包含非线性系数的高阶空间导数。弹性应变能产生于微结构中相之间的晶格失配造成弹性位移，通过Khachaturyan 理论[6]在相场方程中引入弹性应变能，将弹性应变能表达为场变量的函数。已有的关于弹性应变能计算的工作[7-8]，多为使用显格式进行计算的。

本文研究的重点是紧致指数时间差分方法中界面能各向异性和弹性应变能的计算。化学自由能在相场方程中主要表现为高阶空间导数部分，已有的紧致指数时间差分方法通过适当算子分裂格式处理化学自由能，将其归于非线性项的计算，并证明了能量稳定性[9-11]。本文在紧致指数时间差分方法框架下引入了界面能各向异性和弹性应变能的计算，将界面能各向异性和弹性应变能同样归于紧致指数时间差分方法的非线性项统一处理，为其设计了适当的算子分裂格式，证明了算子分裂能够保证能量稳定。并通过镍基合金以及Zr 的氢化物的材料腐蚀相场模型的数值实验，验证了该算法的正确性和能量稳定性。

本文的组织结构如下，第一章介绍了相场模型中界面能各向异性和弹性应变能的引入；第二章主要阐述了含有界面能各向异性和弹性应变能的相场模型的紧致指数时间差分方法，进行了算子分裂格式的能量稳定性以及求解格式的时间精度的证明；第三章给出了镍基合金和Zr 的氢化物材料腐蚀相场模型的数值实验，并验证了求解格式的时间精度；第四章对本文所采用的含弹性应变能的各向异性相场模型的指数时间差分方法进行了总结。

1 含弹性应变能的各向异性相场模型

在本文中，我们考虑含有界面能各向异性和弹性应变能的耦合模型能量方程如式(1.1)所示。

其中，E是系统的总能量，这里考虑了总能量中的化学自由能Ec和弹性应变能Eel。化学自由能Ec可以表达为界面梯度能量项和局部自由能量密度的积分，如式（1.2）所示，其中界面梯度能量中含有各向异性。式(1.2)中，c是成分场变量，而为序参数，和是界面梯度能量项的系数，是3x3 的界面能各向异性矩阵，是关于场变量的多项式形式的局部能量密度，因此局部能量密度公式可导，局部能量密度公式关于两种场变量的偏导数如式(1.3)所示。

其中，

根据 Khachaturyan 理论，在傅里叶空间中，弹性应变能的计算如式(1.4)的积分所示，相场方程中的弹性应变能部分如式(1.5)所示，该项被表达为场变量c或的函数，引入相场方程中，这里以弹性应变能为场变量c的函数进行说明，弹性应变能为场变量的函数的情况与之类似。

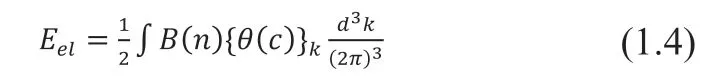
其中，

B(n)是傅里叶空间的弹性相互作用能，是场变量c的结构函数，与分子结构相关。k是傅里叶空间的向量，单位向量表示傅里叶变换，表示傅里叶逆变换，在三维空间中，是一个由四维张量根据物质结构对称性得到的二维刚度矩阵，i、j、k、l分别取1-3 的数值，是应变矩阵，刚度矩阵和应变矩阵决定了弹性应变能的大小和类型。应力矩阵

对总能量方程(1.1)进行变分求解，可以得到描述守恒场变量c的Cahn-Hilliard 方程以及描述结构场变量的Allen-Cahn 方程两种方程组成的耦合方程。Cahn-Hilliard 方程和Allen-Cahn 方程的耦合方程如式(1.6)所示，其中Cahn-Hilliard 方程中的M是迁移率，而Allen-Cahn 方程中的L是扩散系数。

2 指数时间差分方法的求解格式与能量稳定的证明

2.1 指数时间差分方法的求解格式

下面对式(1.6)所示含弹性应变能的各向异性相场方程的紧致指时间差分算法进行推导。假设，模拟区域为空间：

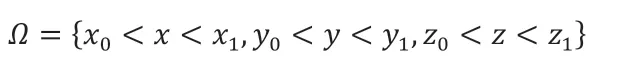
其中，

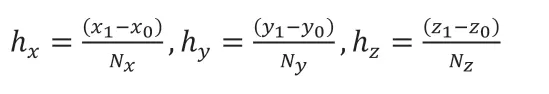
且

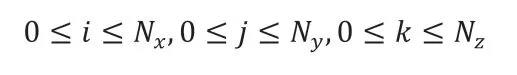
则有：

模拟区域采用周期边界条件[9]。

为了保证能量稳定需要进行算子分裂，后文中对能量稳定的算子分裂格式取值进行了证明。这里直接引入化学自由能分裂算子和，弹性应变能分裂算子，界面能各向异性分裂算子矩阵。算子分裂后的方程如式(2.1)所示。

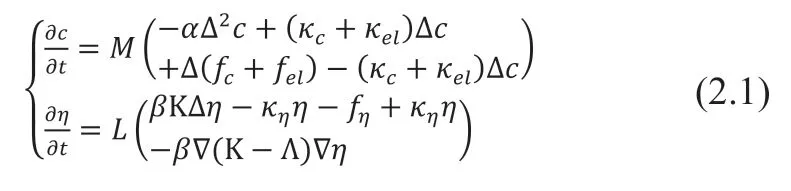
其中，各项异性算子分裂的矩阵如下：

定义二维的方阵G 如下：

则，矩阵A,B,C可以表示为：

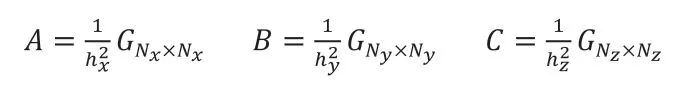
定义运算：

空间离散形式的拉普拉斯算子矩阵可以写成[9]:

将算子代入式(2.1)，得到方程的空间离散形式如式(2.2)所示 ：

根据紧致指数时间差分方法的描述，这里将方程中含有高阶导数的线性项与含有局部能量密度、界面能各向异性、弹性应变能的非线性项g分离，得到式（2.3）。

其中，

在紧致指数时间差分方法中，通过离散傅里叶变换[12]来降低计算复杂度。将矩阵A，B，C根据特征值分解为如下形式：

其中，

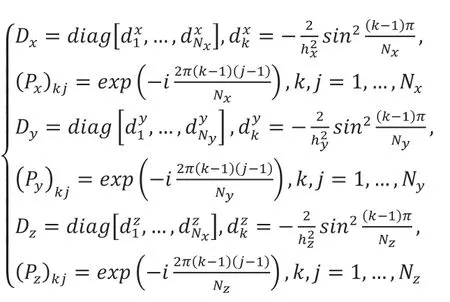
定义算子：

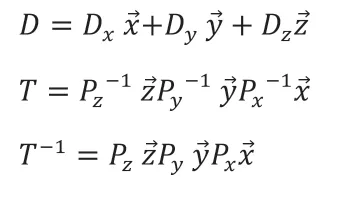
代入式(2.3)，可得式（2.4），经推导后可得式(2.5)。

其中，

在紧致指数时间差分方法中，式(2.5)需要与定义的如下指数时间因子相乘，

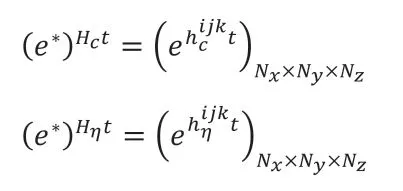
定义两个矩阵的点乘运算：

可得式(2.6)：

式(2.6)两侧均对时间积分可得到如下公式：

积分后，得到的场变量在第n+1 时间步和第n 时间步的迭代关系如式(2.7)所示。

根据拉格朗日多项式近似估计式(2.7)中关于非线性项的积分，得到一阶紧致指数时间差分方法的求解格式(2.8)。

其中，

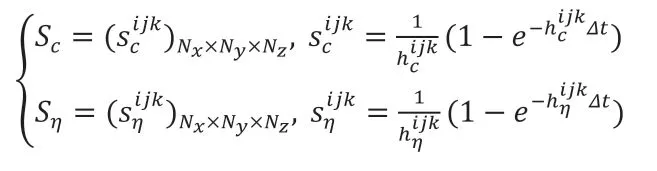
预估校正的紧致指数时间差分方法二阶求解格式如下：

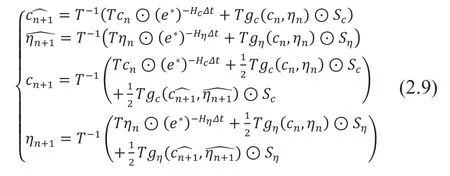
2.2 能量稳定的证明

下面证明2.1 节中得到的含弹性应变能的各项异性相场模型的紧致指数时间差分方法一阶求解格式（2.8）和二阶求解格式（2.9）的能量稳定性。在证明过程中引用了如下引理：

Lemma 2.1对于任意给定的的三维矩阵f和g，有：

Lemma 2.2对于任意给定的的三维矩阵f和g， 如果则：

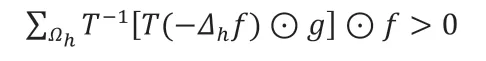
Lemma 2.3（Young’s Inequality）

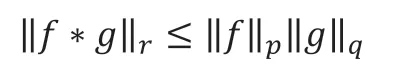
下面是含弹性应变能的各向异性耦合方程一阶指数时间差分方法能量稳定性定理：

Theorem 2.1对于含弹性应变能的各向异性的Allen-Cahn 方程和Cahn-Hilliard 方程的耦合模型（1.6），如果满足条件：

则一阶紧致指数时间差分方法求解格式(2.8)满足能量下降准则。

Theorem 2.1的证明如下：

根据一阶紧致指数时间差分方法公式（2.8），可以得到：

在方程两侧加上：

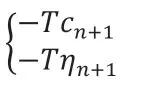
并将方程中的S 替换后可以得到：

其中，

方程两侧进行逆变换可以得到：

方程两侧同时乘上：

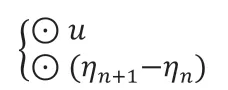
并根据Lemma 2.1进行离散积分，将两个变量的方程合并整理后可得如下方程：

根据局部能量密度和弹性应变能的二阶泰勒展开，得到系统第n个时间步和第n+1 个时间步的能量差的式两种等价形式，式（2.10）和式（2.11）。

根据Lemma 2.2可知，式（2.11）中：

根据Lemma 2.3可得：

因此，若满足Theorem2.1中描述的条件，则式（2.11）的右侧大于0，即：

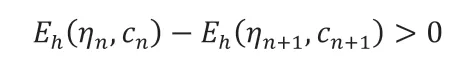
满足能量下降准则，Theorem 2.1得证。

下面是含弹性应变能的各向异性耦合方程二阶指数时间差分方法能量稳定性定理：

Theorem 2.2对于含弹性应变能的各向异性的Allen-Cahn 方程和Cahn-Hilliard 方程的耦合模型（1.6），如果满足条件

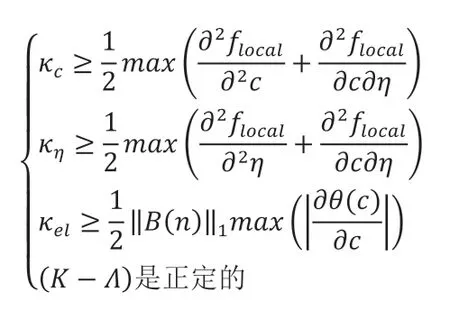
则二阶紧致指数时间差分方法求解格式(2.9)满足能量下降准则。

Theorem 2.2的证明如下：

根据二阶紧致指数时间差分方法公式（2.9）可得：

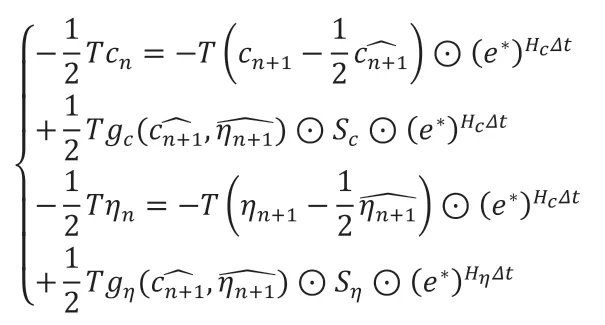
在方程两侧加上：

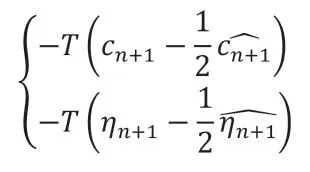
并替换方程中的S可得：

其中r的取值和Theorem 2.1的证明中相同。

方程两侧进行逆变换得到：

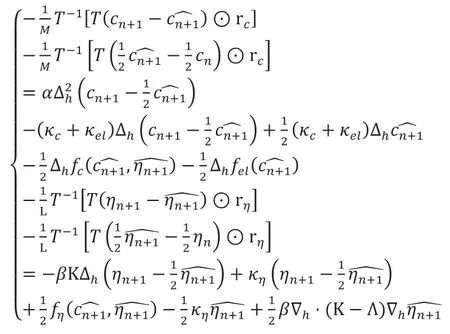
方程两侧乘

根据Lemma 2.1进行离散积分，并根据Theorem 2.1的证明可得如下等式：

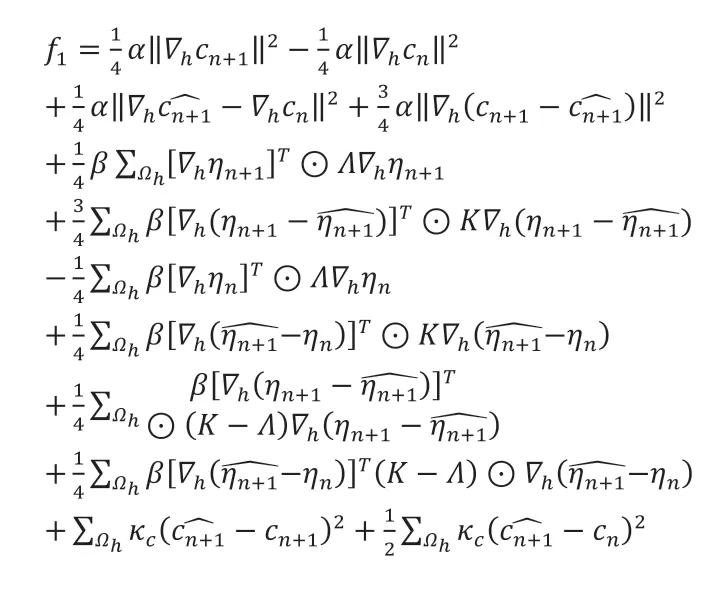
其中，

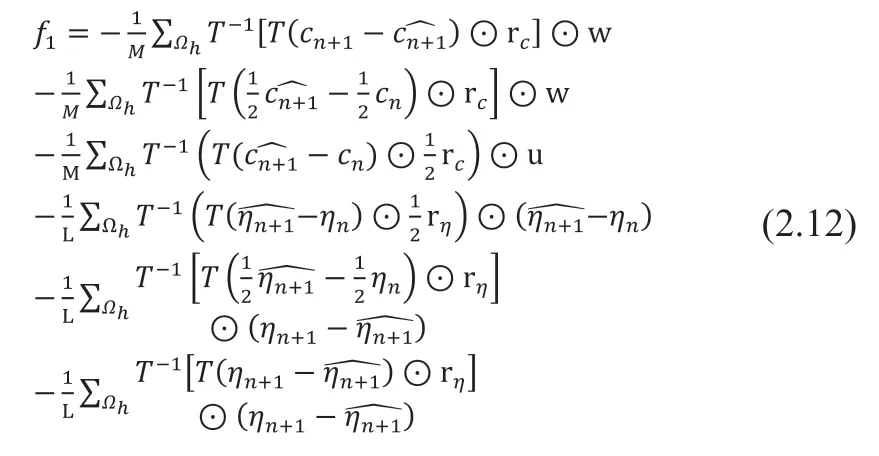
将式中的局部能量密度和弹性应变能进行二阶泰勒展开，整理后得到系统第n个时间步和第n+1个时间步的能量之差的两种等价形式，如式（2.13）和式（2.14）所示：

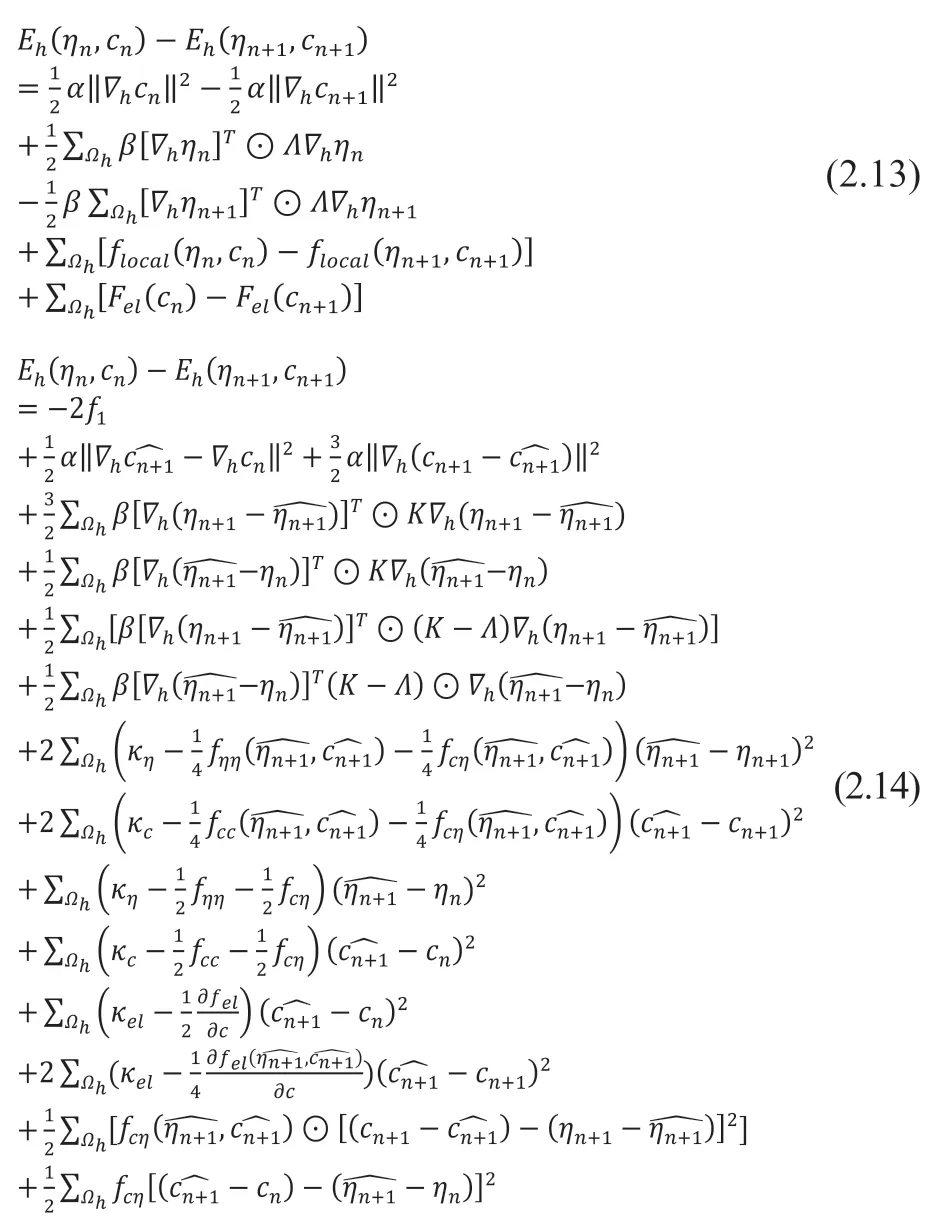
根据Lemma 2.2可知，式（2.12）和式（2.14）中：

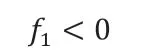
根据Lemma 2.3可得：

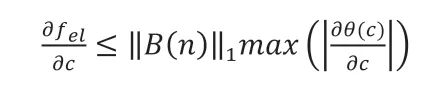
因此，若满足Theorem2.2中描述的条件，则式（2.14）的右侧大于0，即：

满足能量下降准则，Theorem 2.2得证。

2.3 指数时间差分方法的时间精度

下面通过局部截断误差分析指数时间差分方法一阶和二阶求解格式的精度。

为了求解第n 个时间步与第n+1 个时间步的局部截断误差，首先假设第n 个时间步的数值解与精确解相等：

一阶求解格式的局部截断误差定义为：

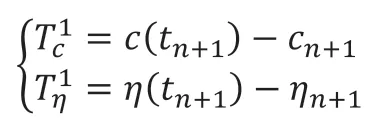
将一阶求解格式的数值解式(2.8)与精确解（2.7）作差并将积分展开可得：

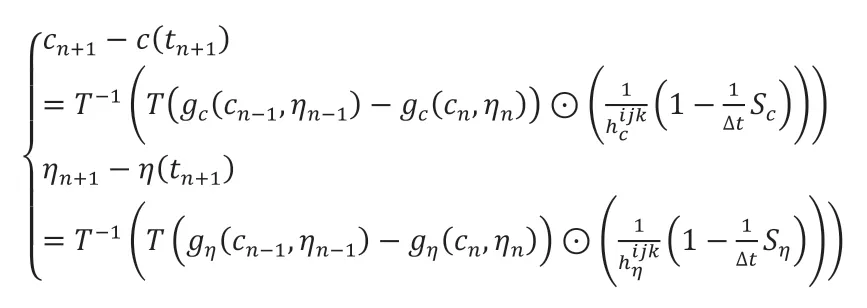
将S代入并进行泰勒展开可得：

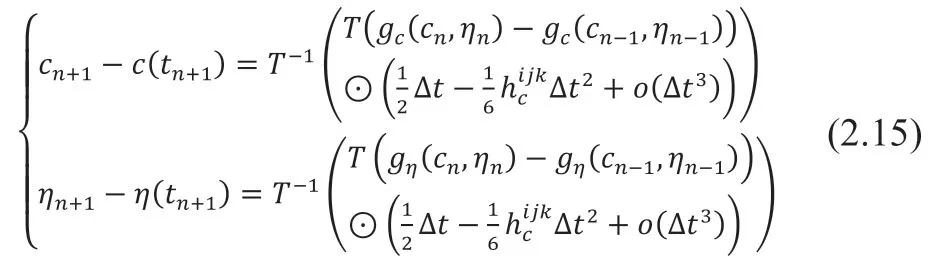
因此，局部截断误差为：

将g代入得到：

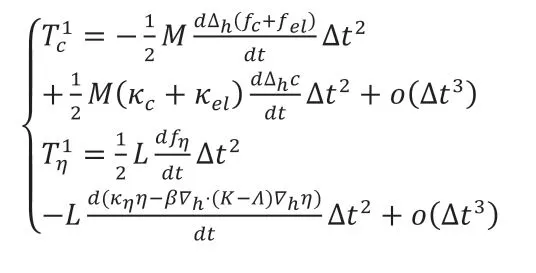
指数时间差分方法一阶求解格式的局部截断误差的主项为二阶，因此该格式的时间精度为一阶。

二阶求解格式的局部截断误差定义为：

将二阶求解格式（2.9）中的预估与校正公式作差可得：

根据式（2.15）可得预估步与精确解的差值：

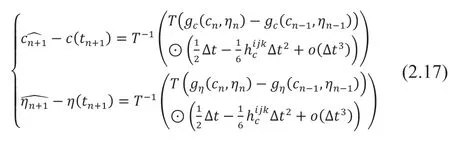
将式（2.16）与式（2.17）相加并整理可得，二阶格式的局部截断误差为：

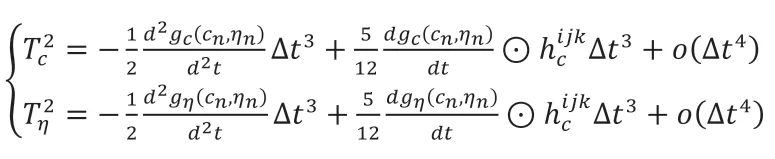
将g和h代入公式可得：

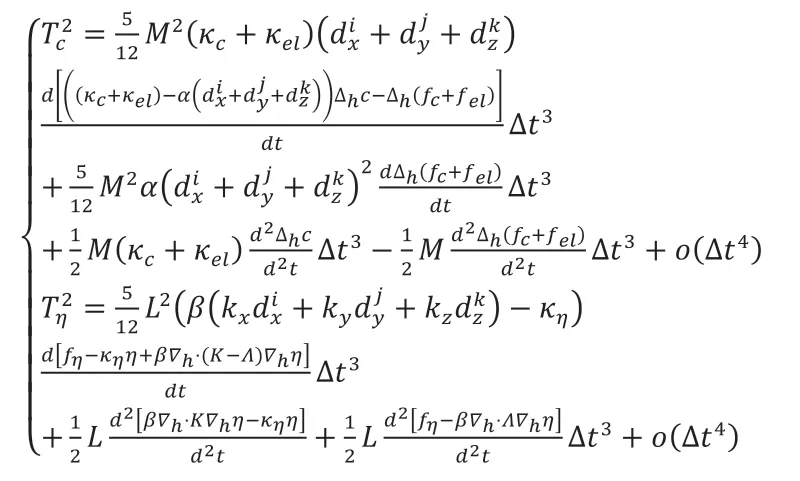
指数时间差分方法二阶求解格式的局部截断误差主项为三阶，因此该格式的时间精度为二阶。

3 数值实验

通过观察镍基合金数值实验和Zr 的氢化物堆叠数值实验两个相场模型的数值模拟结果，对含有界面能各向异性和弹性应变能的紧致指数时间差分方法的正确性以及算子分裂格式的能量稳定性进行验证。本文中的数值实验是在中国科学院计算机网络信息中心的超级计算机“元”二期计算系统的 CPU节点进行。以下数值实验均为三维模拟，为方便观察，实验结果为模拟区域中心截面截图。

3.1 镍基合金的数值实验

镍基合金的数值实验[13]模拟了高温下的单一无序相分解成低温下的富溶质的有序相和溶质贫化的无序相的过程。该数值实验的相场模型不含界面能各向异性，因此我们关注的重点是弹性应变能的作用。其相场耦合方程如式(3.1)所示。

其中，

数值实验中的参数均采用无量纲化后的取值。其中，A1= 62.5，A2= 25，A3= 12，A4= 6.25，C'= 0.2，C''= 0.6，迁移率M为1.0，扩散系数L为1.0，界面梯度能量的系数的取值为：

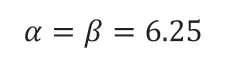
弹性应变能计算相关的弹性应变矩阵和刚度矩阵如下：

模拟的时间步长为1e-2，模拟的总时间为20.0，网格尺寸为1.0，三维的模拟区域大小为128×128×128。在模拟的初始状态，模拟区域中央给定一个半径为8 个网格宽度的新相粒子，场变量c的初始值为0.4 和0.65，场变量的取值为0 和1.4。[14]算子分裂参数取值如下：

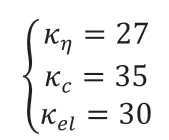
图1 不含弹性应变能的镍基合金数值实验的模拟结果Fig.1 Simulation results of numerical experiment of Ni-based alloy without elastic strain energy

图2 含有弹性应变能的镍基合金数值实验模拟结果Fig.2 Simulation results of numerical experiment of Ni-based alloy with elastic strain energy

以下分别进行了无弹性应变能和有弹性应变能的模拟。无弹性应变能的场变量c在迭代步数t=0,1000,2000 的模拟结果如（图1）所示，没有弹性应变能的作用，粒子随着时间生长，演化成了球形；有弹性应变能的场变量c在迭代步数 t=0,1000,2000的模拟结果如（图2）所示。在弹性应变能的作用下，粒子随时间生长，演化成了方形。其能量下降曲线如（图3）所示，能量稳定。

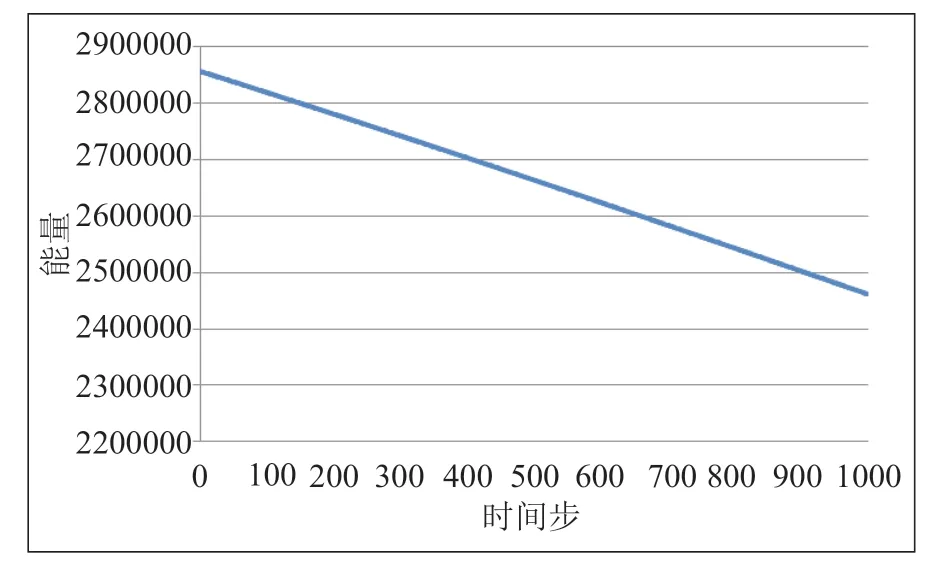
图3 镍基合金数值实验的能量下降曲线Fig.3 Energy decline curve of numerical experiment of Nibased alloy

3.2 Zr 的氢化物堆叠数值实验

Zr 的氢化物堆叠数值实验[8]是描述氢化物在Zr 中的堆积结构形成和转变的三维相场模型。该数值实验既含有界面能各向异性，又含有弹性应变能。其耦合方程如式(3.2)所示：

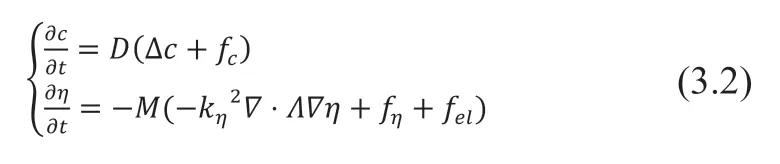
其中，

w为1.848e9，迁移率M为5e-4，扩散系数D为1.2302e-10，界面梯度能量的系数的取值为：

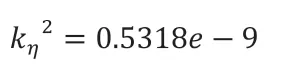
界面能各向异性矩阵取值如下：

弹性应变能计算相关的弹性应变矩阵和刚度矩阵为：

模拟的时间步长为1e-7，模拟的总时间为2e-4，网格尺寸为1e-9，三维的模拟区域大小为128×128×128。在模拟的初始状态，模拟区域中央给定一个半径为10 个网格宽度的新相粒子，场变量c的初始值为0.1 和0.5982，场变量的取值为0 和1.0。

紧致指数时间差分方法算子分裂参数取值为：

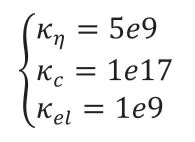
下面分别进行了有无界面能各向异性和有无弹性应变能的四组数值实验。无界面能各向异性和弹性应变能，模拟结果如（图4）所示，氢化物逐渐演化为球体；有弹性应变能，无界面能各向异性，如（图5）所示，氢化物发生旋转，成为椭球体；无弹性应变能，有界面能各向异性，模拟结果如（图6）所示，氢化物在界面能各向异性的作用下变成圆盘；有弹性应变能和界面能各向异性，模拟结果如（图7）所示，氢化物在界面能各向异性的作用下变成圆盘，在弹性应变能的作用下发生旋转，但是在两者的共同作用下，氢化物旋转的角度小于只有弹性应变能作用的情况下的旋转角度。其能量下降曲线如（图8）所示，能量稳定。

图4 无界面能各向异性、无弹性应变能的Zr 的氢化物数值实验的演化过程Fig.4 Evolution process of numerical experiment of Zr-hydride without interface energy anisotropy and elastic strain energy

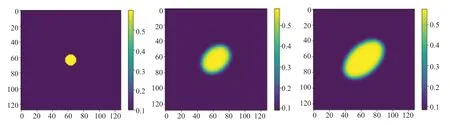
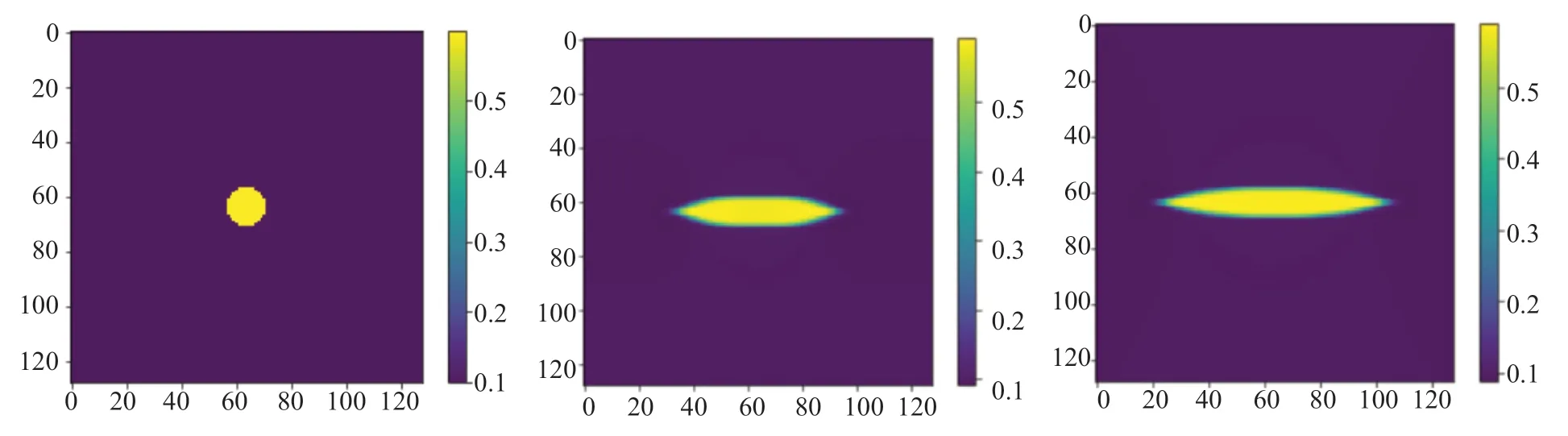
图6 有界面能各向异性、无弹性应变能的Zr 的氢化物数值实验的演化过程Fig.6 Evolution process of numerical experiment of Zr-hydride with interface energy anisotropy and without elastic strain energy

图7 有界面能各向异性，有弹性应变能的Zr 的氢化物数值实验的演化过程Fig.7 Evolution process of numerical experiment of Zr- hydride with interface energy anisotropy and elastic strain energy

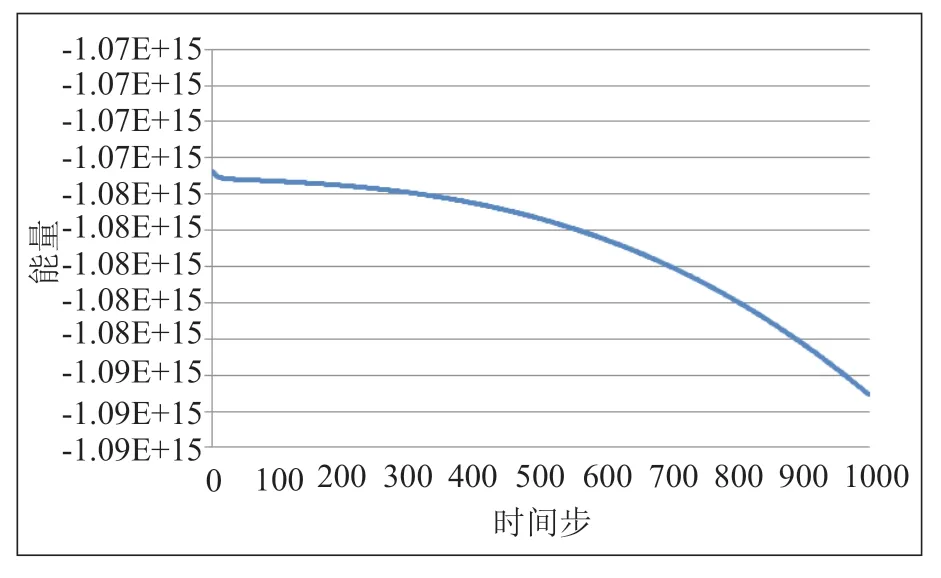
图8 Zr 的氢化物数值实验的能量下降曲线Fig.8 Energy decline curve of numerical experiment of Zrhydride

下面进行了一系列时间步长倍增的实验用以验证指数时间差分方法的时间精度。时间步长分别取（其中δ =4e-9），以相同初始值运行至同一时刻T= 2.56e-5，将时间步长dt = 1e-9 作为基准解。计算了指数时间差分方法一阶格式的L2误差和收敛率如表1所示，收敛率的值接近1；二阶格式的L2误差和收敛率如表2所示，收敛率的值接近2，验证了求解格式的时间精度。

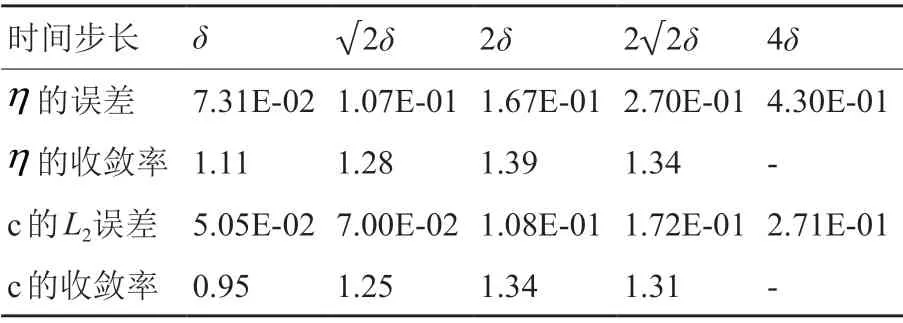
表1 指数时间差分方法一阶求解格式的误差Table 1 The error of the first order scheme of the Exponential Time Difference method

表2 指数时间差分方法二阶求解格式的误差Table 2 The error of the second order scheme of the Exponential Time Difference method

4 结论与展望

本文在紧致指数时间差分方法框架下引入了界面能各向异性和弹性应变能的计算，将界面能各向异性和弹性应变能归于紧致指数时间差分方法的非线性项统一处理，通过积分和预估校正的二阶近似进行计算，为保证能量稳定，设计了界面能各向异性和弹性应变能的算子分裂格式，并对算子分裂格式的能量稳定性进行了数学证明。通过材料腐蚀相场模型的数值实验，观察了界面能各向异性和弹性应变能对场变量演化的影响，验证了含弹性应变能的各向异性相场模型的指数时间差分方法算子分裂格式的能量稳定性。本文使用超级计算系统“元”对指数时间差分方法的格式精度和能量稳定性进行了验证，在后续的工作中，拟使用“天河二号”超级计算机进行并行扩展性的测试。[15-16]本文仅得到了指数时间差分方法的一阶和二阶求解格式，更高阶的求解格式及其稳定性有待进一步探索。

利益冲突声明

所有作者声明不存在利益冲突关系。