基于矩阵值因子算法的企业年金投资组合建模与并行求解

杜首燕，陆忠华

1. 中国科学院计算机网络信息中心，北京 100190

2. 中国科学院大学，北京 100049

引 言

在人口老龄化的危机下，单一的、以政府为主导的社会养老金制度面临着平衡难以持续、财政负担不断加重的问题，因此大力发展第二支柱企业年金是中国养老金养老保险体系改革的必然方向，通过在市场中投资运营，来促进企业年金的保值和增值是缓解我国养老金缺口的最佳方法。

郭辰、施秋圆、郭梦云(2013)[1]限制货币市场工具、银行定期存款、国家债券，企业债和股票的投资比率，并使用均值-CVaR 模型建立了公司年金的资产配置模型，以在特定工资替代率目标下获得最佳投资组合。胡秋明、景鹏(2014)[2]建立DCCGARCH-CVaR 模型刻画资产间动态相关关系和度量投资组合风险，构建企业年金基金资产结构动态调整模型。余睿(2015)[3]引入负债驱动型投资组合最优化决策，运用蒙塔卡洛模拟方法，通过死亡率-金融市场联合模型对企业年金在未来年份的投资收益进行测量，并在各置信水平下与传统方法进行比较。赵自强、魏新雅(2017)[4]运用随机最优控制理论，构建并求解企业年金最优资产配置比例的HJB 方程，得出企业年金最优资产配置比例的解析解。李洁、彭燕、曹晓政(2017)[5]采用Markowitz 的均值方差模型，在现有企业年金投资约束下，对不同投资组合下主要投资工具的收益和风险进行了计量。方中书(2018)[6]通过分析企业年金相关的基金投资工具，选取相应变量数据，运用改进后的均值-方差模型对不同预期收益率的投资组合进行测算分析，将数理金融分析方法结合LINGO 软件运用于企业年金基金的投资组合管理与优化。李燕敏(2018)[7]运用综合分析法，从定性和定量两方面分析了我国养老金融发展概况和主要商业银行提供的养老金融产品现状。温家琪(2019)[8]研究了含有违约风险的缴费确定型企业年金的投资策略问题，运用Hamilton-Jacobi-Bellman方程进行求解，并进行数值分析，还改进了将企业年金投资于多个可违约债券的组合。王超、杨德平(2019)[9]基于均值-方差模型作为主要理论基础，使用Matlab 软件中的GUI 工具开发投资组合优化系统。Ben Mingbin Feng、Zhenni Tan、Jiayi Zheng(2020)[10]对大型可变年金投资组合进行估值，确定了有效估值框架中的三个主要组成部分，提高了估值的准确性并无需任何额外的计算资源。

基于以上文献综述，通过分析我国企业年金的投资策略可发现，进行单一资产的投资较多，但没有从投资组合的协方差等各资产相关性角度制定的投资策略，这样会导致更关注于投资的短期收益，不利于确定整体的风险和收益目标。此外，在将经典的风险投资模型Markowitz 均值-方差模型进行实际应用时，存在每个资产在总资产数量中的占比没有上限的问题。再者，在实际应用过程中，当投资组合中资产数量过多时，协方差矩阵的大小变得太大，存在对基本输入所要求的估计量非常大的问题，而且求解最优化投资组合模型往往耗时过长，无法满足实际交易的需求。如果上述计算层面上的问题得不到有效解决，将严重阻碍现代投资组合理论和数量化投资管理技术的实际应用进程[11]，不利于我国资产管理市场的健康发展。

因此，本文关注安全性和收益性以及流通性三大企业年金投资原则，从协方差矩阵方面进行企业年金的投资组合模型研究，改进模型的约束条件来解决每个资产在总资产数量中的占比没有上限的问题，应用矩阵值因子算法来解决随着资产数量增加，协方差矩阵过大的问题，基于CVXOPT 求解器、遗传算法和粒子群算法进行最优值求解，并并行求解模型，在达到一定收益的条件下降低投资组合的风险性。

1 基于矩阵值因子算法的均值-方差投资组合优化模型构建

1.1 基于矩阵值因子算法的均值-方差优化模型

1.1.1 带投资约束条件的均值-方差优化模型

资产组合优化是研究如何在各种复杂的市场环境中有效地配置资产，从而最大程度地对投资风险进行分散并最大化投资收益率。在证券市场上，投资管理机构和投资者基于各种考虑，通常对资产配置有初步要求，而相应的投资组合也必须满足市场和投资者的要求。对企业年金而言，在人社部制定的《关于扩大企业年金基金投资范围的通知》中指出，企业年金投资股票、股票基金、混合基金、投资连结保险产品、股票型养老金产品的比例，合计不得高于投资资产净值的30%。因此，研究带数量约束的风险资产的投资组合可以满足企业年金和市场实际操作的需要[12]。

因此，构建带上界约束条件的均值-方差投资组合优化模型，且不允许卖空，参数如表1 所示：

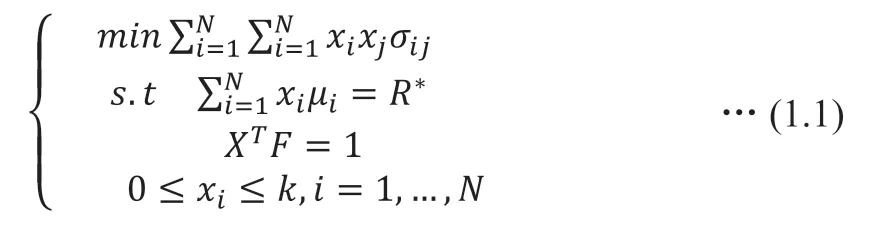
表1 均值-方差投资组合优化模型参数Table 1 Mean-variance portfolio optimization model parameters

1.1.2 已实现协方差矩阵

本文采用宋鹏(2017)[13]提出的方法进行已实现协方差矩阵的构造，当投资组合中有两种风险资产时，在第天风险资产的已实现协方差矩阵的构建公式如下：

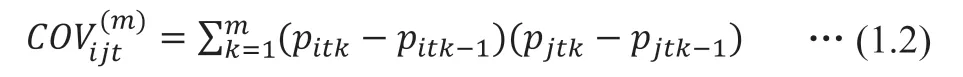
已实现协方差矩阵用来描述风险资产间的相关性关系，清洗后的已实现协方差矩阵用来进行矩阵值因子分析，目的是为了解决在数据容量越来越大时，维度越来越高时传统计算对高维协方差矩阵的计算不便，待估参数过多，累积误差大的问题。

1.1.3 可预测矩阵值因子模型

矩阵值因子算法一方面通过对构建的高维已实现协方差矩阵进行矩阵值因子分析，探究协方差元素之间的相关性联系，另一方面，该算法采用基于Cholesky 分解和向量自回归（VAR）方法对可预测矩阵值因子模型进行降维建模和下一投资区间的协方差矩阵预测。

矩阵值因子算法过程阐述如下[13]：

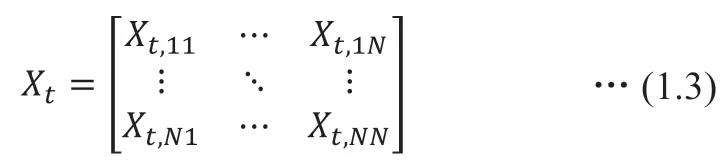
应用Cholesky 分解方法，得到：

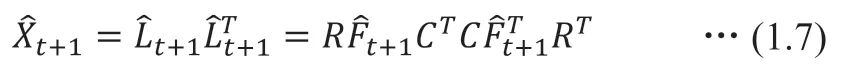
1.2 基于矩阵值因子算法的均值-方差优化模型的遗传算法求解

基于矩阵值因子的均值-方差投资组合优化问题是非线性优化问题。尽管在Markowitz 的投资组合理论中，提供了一种通过求解拉格朗日函数，将其转换为最小方差点的方法来得到模型最优解的确定性方法，但在实际应用中，随着数据规模的增大，计算量和参数估计量都会变得特别大，会出现无法求解的情况[14]。而遗传算法擅长解决非线性优化问题，通过在迭代过程中不断增加新个体，选择合适的算子以及遗传操作，再执行遗传算法进行全局寻优搜索。因此，本文使用遗传算法来求解该投资组合优化问题。

本文用于求解投资组合优化模型的遗传算法求解步骤如下：

步骤一：采用二进制编码机制对个体进行编码，用随机生成的染色体数目来进行种群初始化。在投资组合优化问题方面，每个染色体代表投资组合单个风险资产的权重，并被优化来得到最终解。

选择操作采用二元锦标赛选择法，该方法的操作步骤如下：

（1）每次选择的个体数量为两个。

（2）从个体中随机选择两个个体，其中每个个体被选中的概率都是相同的，然后根据每个个体的适应度值，选择适应度值最高的个体进入下一代种群。

（3）重复进行步骤2，直到达到设定的种群大小，种群的规模没有变化。

步骤二：夏普比率作为评估函数，用于评估每个染色体的适应度，种群中每个个体的适应度可以用来判断是否满足算法的收敛性。夏普比率是期望收益率与风险的比值，用于计算投资组合中每个风险单位带来的超额收益，数值越大代表该投资组合能获得的收益率越高。因此，如果满足算法收敛准则，则输出最优个体和由其表示的最优解，否则执行步骤三。

夏普比率方程：

步骤三：根据适应度选择进入下一代种群的个体，适应度高的个体有更高的概率进入下一代种群，相应的，适应度过低的个体会被淘汰。

步骤四：交叉操作是指替换并重组两个父代个体的结构的一部分以生成新个体的操作。交叉操作可以在种群中生成新个体，从而提高了遗传算法的搜索效率。

本文中的交叉操作使用均匀交叉（也称为一致交叉）来生成新个体，这意味着两个成对个体的每个基因座处的基因都以相同的交叉概率进行交换，并形成了两个新个体。

步骤五：只采用交叉算子会导致收敛到局部最优的情况，这是求解投资组合过程中所不希望发生的。因此需要和变异算子相结合，共同产生新个体。其中，变异是指以一定概率对个体执行变异操作，并以较小概率随机改变向量的值。变异的好处是能产生上一代种群没有的但是有用的基因结构，增大求得全局最优解的可能性。

本文中的变异操作使用均匀变异，替换个体编码字符串中每个基因组上的基因值，以一定的变异概率来生成新个体，这可以提高种群中个体的多样性，并使算法能够处理更多的模式；

步骤六：根据遗传的基本操作（交叉操作和变异操作）产生下一代种群，按照给定的迭代次数进行种群的迭代更新，返回步骤二。

1.3 基于矩阵值因子算法的均值-方差优化模型的粒子群算法求解

粒子群算法是一种典型的群体智能优化算法，1995年，R.C.Eberhart 和J.Kennedy 首先 提 出 了 模拟自然界生物和群体智能的粒子群算法。该算法首先随机初始化粒子，然后通过重复迭代找到最佳解。在每次迭代中，粒子通过确定个体极值和全局最优值来更新速度和位置。相比遗传算法，粒子群算法不具有遗传算法的交叉变异操作，且参数相对少，因此搜索效率明显提高[15]，在科研和工程应用中得到了广泛的研究。

本文用于求解投资组合优化模型的粒子群算法求解步骤如下：

步骤一：设置粒子群规模，假设种群中有个粒子，设置粒子群中粒子的速度区间，粒子的速度和位置在整个搜索空间中进行初始化，粒子的位置信息在整个搜索空间中表示。

步骤二：同遗传算法，夏普比率作为评估函数，用于评估每个染色体的适应度。

步骤三：确定每个粒子的个体极值，即每个粒子找到的历史上最优的位置信息，将新位置与个体极值比较，如果新位置优于个体极值，则个体极值更新为新位置的值，否则保持个体极值不变。

步骤四：确定粒子的全局最优值，即从所有个体的个体极值中找到一个全局最优值，并与历史最优值相比较，最佳的值作为粒子的全局最优值。

步骤五：更新粒子的速度，计算公式为：

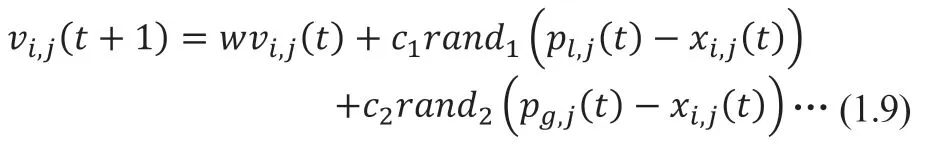
步骤六：更新粒子的位置，计算公式为：

步骤七：重复给定的迭代次数，将粒子群收敛到全局最优值。

1.4 均值-方差优化模型的矩阵值因子算法和遗传算法并行化

1.4.1 算法思想

在实际的投资组合的应用中，企业年金被期望能够在确保安全性的同时实现资产的保值增值，从而充分发挥养老金保障养老的作用，因此配置多种资产用来分散风险是基本操作。当投资组合的资产规模过多时，传统的求解算法会存在耗时时间长，且不能快速有效收敛到最优解的问题，因此，进行投资组合模型的并行化研究是相当必要的[16]。

在单线程时，算法收敛到最优解的速度与空间遍历的速度一致。在多线程的情况下，每单位时间处理的数据量随线程数线性增加。对于金融领域的较为复杂的求解问题，在仅仅追求较优解而不是强求最优解的前提下，进行并行计算可以减少搜索时间[17]，提高求解的质量，更好地满足实际应用需 求[18]。因此，为了衡量该矩阵值因子算法构建的投资组合优化模型通过并行计算可获得的性能改进，本文在高性能计算环境中进行了数值实验，其中遗传算法的迭代次数为30 次，其他参数同上文所述。

图1 表示基于矩阵值因子算法的均值-方差优化模型的并行求解流程图，首先对风险资产价格数据计算对数收益率，表示风险资产的收益情况，然后基于对数收益率形式的时间序列数据构建高维已实现协方差矩阵，在多个处理器上同时进行矩阵值因子算法，得到建模和预测的已实现协方差矩阵，作为带投资约束的均值-方差投资组合优化模型的协方差矩阵，也就是风险度量。接下来结合传统均值-方差模型的思想，加入投资约束条件构建基于矩阵值因子算法的均值-方差投资组合优化模型，并进行最优值求解，遗传算法的求解在不同处理器上分别进行。

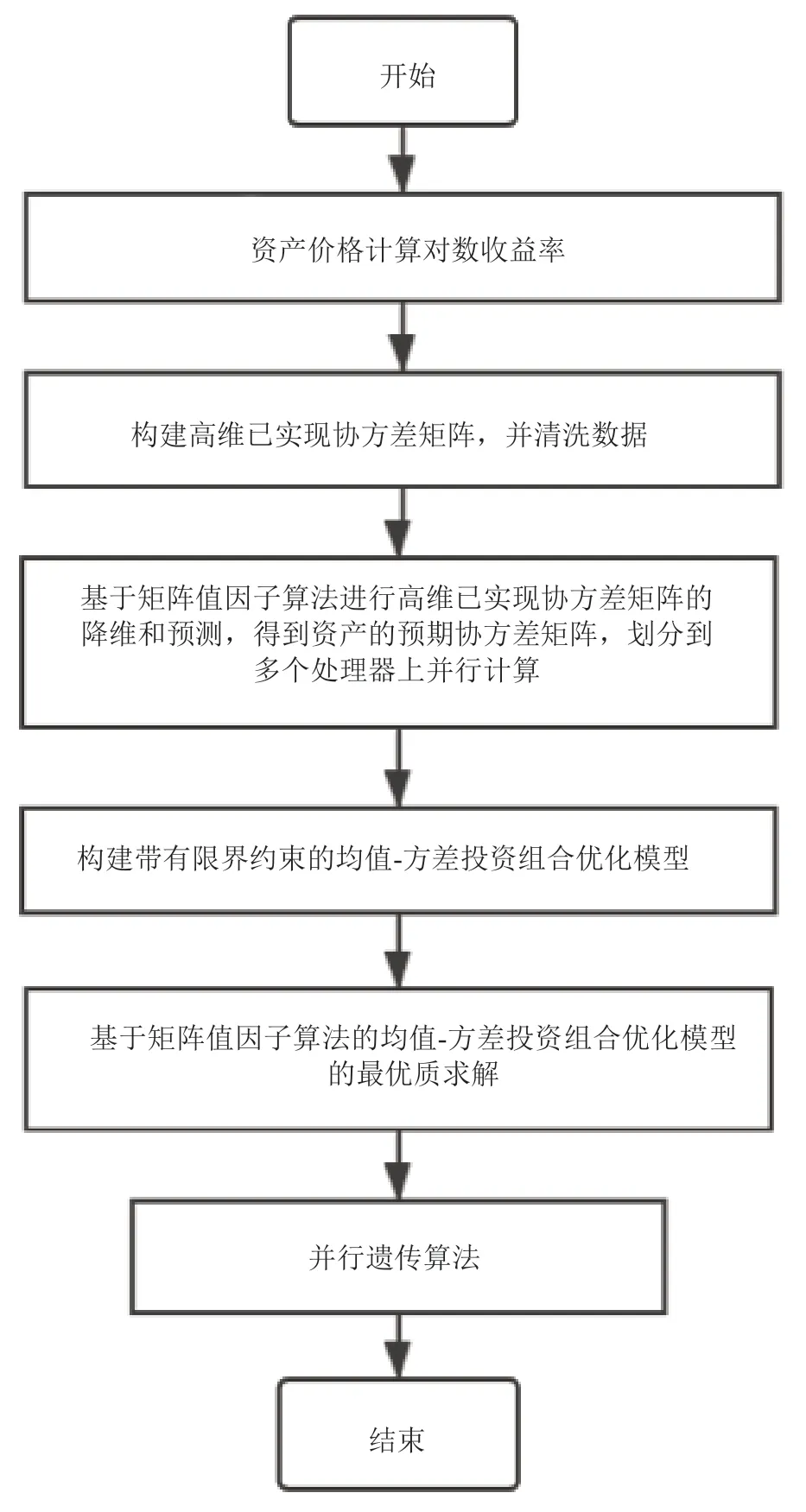
图1 基于矩阵值因子算法的均值-方差投资组合优化模型并行求解流程Fig.1 Parallel solution process of mean-variance portfolio optimization model based on matrix-valued factor algorithm

1.4.2 算法过程

本文主要对投资组合优化模型中两部分进行并行优化，第一部分是应用矩阵值因子算法建模和预测协方差矩阵的部分进行并行化。在基于矩阵值因子算法的投资组合模型中，对矩阵值方法的并行计算可以缩短构建因子矩阵的时间，提高对资产间的相关性进行分析预测的效率。思想是将已清洗后的数据分别构建资产间的已实现协方差矩阵，将预测周期的天数均匀分配到处理器上，多余的预测周期的天数计算划分到最后一个处理器上，每个处理器都进行高维协方差矩阵的降维和预测操作，最终合并得到总周期天数的预测矩阵。

第二部分是在应用遗传算法进行最优值求解的部分进行并行化。并行化遗传算法求解在投资组合中的应用可以加快计算速度，通过同时使用多个线程运行，可以提高最优解的准确性并加快求得全局最优解的速度。此外，遗传算法随机搜索最优解，具有隐式并行性，适合并行计算。思想是将每一代中的初始种群进行划分，分别在独立的处理器中进行遗传算法的基本操作，每个个体都进行遗传优化，经过一系列遗传操作后，将每个小种群中的最优个体选择出来再继续进行遗传操作，最后得到搜索空间中的全局最优个体[14]。

其中，并行遗传算法的计算流程如下：

（1）种群初始化

本文采用二进制编码方式，个体的基因型是由二进制编码字符串来表示，取值由0 和1 组成。定义种群的初始规模为，表示种群中有个个体，对每个个体进行随机初始化，同时对每个个体的权重增加约束条件，对个体的权重进行归一化处理，使得权重和为1，由公式确定。

（2）计算适应度

适应度函数选择夏普比率来衡量投资组合的效用，夏普比率越大，表示资产单位风险能获得的收益越高，个体的适应度越大，遗传概率越大。

（3）并行种群分组

将种群分到多个处理器中进行计算，每个处理器中是一个子群，划分为个子群，根据种群数与处理器数的关系决定拆分的子种群包含的个体数。如果种群规模小于处理器数，则每个处理器中子群规模为1，并分配到种群规模的处理器上进行并行计算；如果种群规模可以整除处理器数，则种群均匀分配到每个处理器上，子群大小相同；如果种群规模不能整除处理器数，则将能整除大小的种群数分别均匀分配到每个处理器上，然后将多余的种群数分别加到从开始的处理器上。

（4）遗传操作

在种群规模内，对每个种群中的个体分别进行遗传算法基本操作，选择操作采用二元锦标赛选择法，即随机选择两个父个体生成一个新个体。交叉操作采用均匀交叉操作生成新个体，扩大解空间的范围。变异操作采用均匀变异方法，将个体编码字符串中的原始基因值替换为符合特定范围的均匀分布的随机数，并设置交叉和变异概率，完成一次遗传算法。

（5）并行种群合并

将每个子种群的个体合并到一起，从中选择出适应度最高的个体，至此完成一次并行化遗传算法计算。

（6）种群迭代

将迭代得到的最高适应度的个体代入投资组合模型进行投资组合收益率、风险、夏普比率和最优资产配置的求解，得到该次迭代的最优解，并把得到的种群作为下一代种群的初始种群，重复迭代直到达到要求的迭代次数。图2 是并行遗传算法的求解流程图。

图2 并行遗传算法求解流程Fig.2 Parallel genetic algorithm solution process

2 实验设计与结果分析

2.1 实验环境设置

为了衡量投资组合模型并行优化后获得的性能提升，本文在新一代超级计算机“元”的高性能计算环境进行数值实验，并从并行计算性能方面对数值实验结果进行合理分析。并行环境参数如下表2所示。

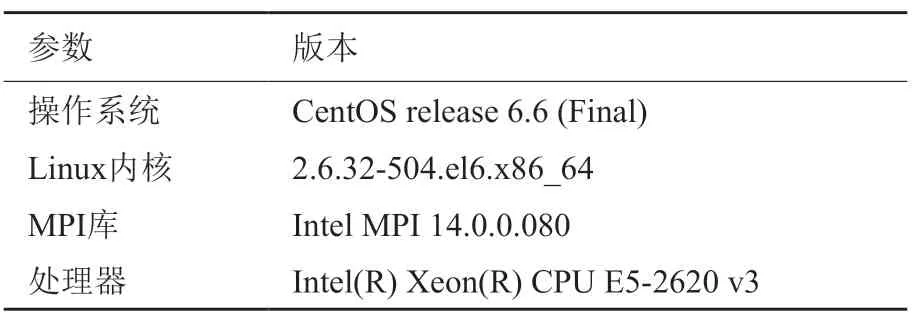
表2 环境参数Table 2 Environmental parameters

2.2 实验数据集

本文基于风险资产的数据进行企业年金投资组合的研究，实验数据集是选取的2013年9月11日至2016年8月31日的深交所16 种行业指数的高频数据，共726 个交易日，16 个行业分别为采矿行业、建筑行业、制造行业、餐饮行业、批零行业、文化行业、科研行业、农林行业、运输行业、IT 行业、地产行业、金融行业、商务行业、水电行业、公共行业、综企行业。采用Callot 和Kock(2017)[19]的方法对数据进行清洗，操作方法为，在每个以交易日为单位构造的已实现协方差矩阵中，如果某一天中的某元素的值超过了该天均值的正负三倍标准差，则标记该元素的位置和发生日期。如果一个矩阵中被标记的元素超过25%，则该天的协方差矩阵被认为是异常，通过计算共去掉了18 个协方差矩阵，其中每日的时间序列以资产的对数收益率表示，最终得到708天的协方差矩阵可用于矩阵值因子分析。

2.3 基于矩阵值因子算法的均值-方差优化模型的实验设计

将清洗后的高维已实现协方差矩阵划分为建模和预测两部分，设为600 天的建模窗口长度，108 天的预测窗口长度，将可预测矩阵值因子模型用于降维和预测高维已实现协方差矩阵，矩阵值因子模型中的Cholesky 分解方法实现高维已实现协方差矩阵的降维和待估参数的缩减，矩阵值因子模型的向量自回归方法实现预测窗口长度108 天的已实现协方差矩阵，作为基于企业年金的投资组合模型的资产间相关性联系和风险度量。其中，收益率定义为对数收益率。建立具有投资约束的均值方差优化模型。目标函数是在预期收益的条件下使投资组合的总方差最小化，从而确保企业年金投资的安全性和收益性。为了能有效求解该二次规划模型，尝试CVXOPT 求解器、遗传算法和粒子群算法三种求解方法。

2.4 基于矩阵值因子算法的均值-方差优化模型的最优值求解的实验结果

2.4.1 CVXOPT 求解器求解均值-方差优化模型的实验结果

在求解投资组合时，当投资组合模型的目标函数为线性，可以通过做图求解线性规划，但是当目标函数包含二次项时，则需要使用特定的求解方法。本文所构建的基于矩阵值因子算法的均值-方差优化问题可归类为二次规划问题，因此可通过Python中CVXOPT 求解器进行最优值求解。该求解器用于求解二次规划问题，首先将目标函数和限制条件都转化为二次规划问题的标准形式，参数分别用矩阵形式表示，然后调用CVXOPT 求解器中的优化函数solvers.qp 进行求解，因此求得该目标函数在满足设定限制条件下的最优资产配置的权重值。该投资组合优化模型可采用表3 表示当期望收益率取值为0.006，0.01，0.014 时，在取前200 天日度收益率的均值作为收益期望的条件下，基于矩阵值因子算法的均值-方差优化模型采用CVXOPT 求解器，求解得到的最好方差、均值方差、运行时间和收益率。

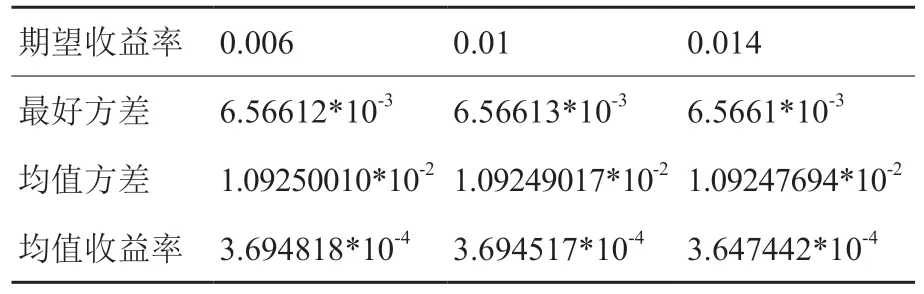
表3 基于矩阵值因子算法的均值-方差优化模型的CVXOPT求解Table 3 CVXOPT solution of the mean-variance optimization model based on matrix-valued factor algorithm

2.4.2 遗传算法求解均值-方差优化模型的实验结果

对于遗传算法，种群规模初始化为50 个个体，即50 种不同权重的组合。编码过程对每条染色体的权重进行随机初始化。收益期望是前200 天日度收益率的均值，不包含无风险利率。

然后对种群进行选择操作，使用夏普比率作为适应度函数来计算每个染色体的适应度值，并根据每个染色体适应度的大小确定进入下一代种群的染色体。 投资组合的收益增加，风险越低，则夏普比率越高，适应度越大，适应度越高的子代进入下一代种群的概率越大。

同时对适应度函数加了静态惩罚约束，原理是当投资组合的收益率低于预期收益率时，通过将惩罚项集成到适应度函数中，可以降低违反约束的个体的适应度，本文中惩罚系数为常数，不会随着算法迭代变化，本文中的惩罚函数构造为：

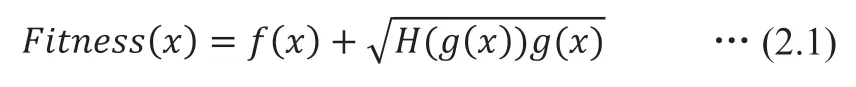
然后执行种群的交叉和变异操作。其中，交叉概率设置为0.85，变异概率设置为0.025，生成的新一代种群作为初始值进入下一个迭代过程，迭代次数为200 次，直到满足终止条件为止。表4 是对优化模型的遗传算法求解的结果。

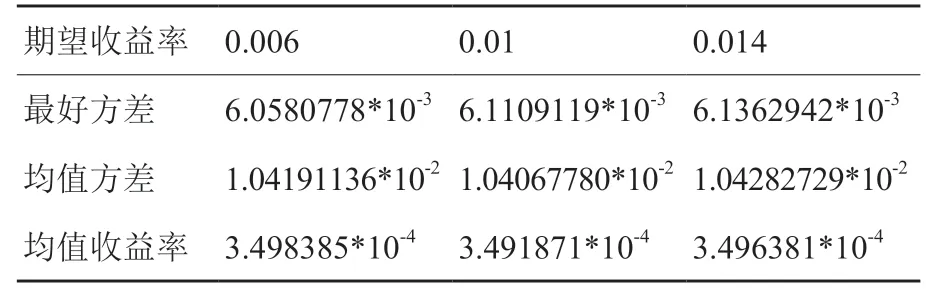
表4 基于矩阵值因子算法的均值-方差优化模型的遗传算法求解Table 4 Genetic algorithm for solving the mean-variance optimization model based on matrix-valued factor algorithm

投资组合模型另一个评价指标为夏普比率，即在一定时间区间内，投资组合相对于无风险利率的收益情况，并根据假定的风险来衡量金融资产的绩效，包括非系统性风险和系统性风险。图3 是当期望收益率取值为0.01 时，在预测周期108 天中，基于矩阵值因子算法的均值-方差优化模型的CVXOPT 求解方法和遗传算法求解方法的夏普比率，可看出基于遗产算法求解的模型的夏普比率更平稳，具有更稳定的收益情况。

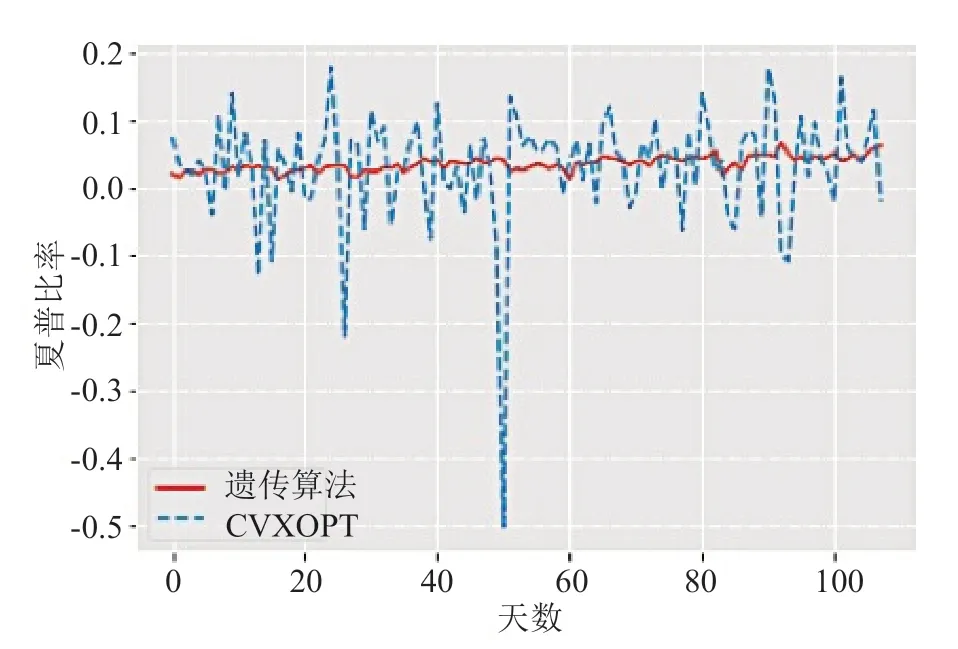
图3 遗传算法和CVXOPT 求解模型在108 天周期中的夏普比率Fig.3 Sharpe ratio of genetic algorithm and CVXOPT solving model in 108 days

2.4.3 粒子群算法求解均值-方差优化模型的实验结果

对于粒子群算法，设置粒子群规模为600，即种群中有600 个粒子，在粒子群的整个搜索空间中随机初始化粒子的速度和位置。同遗传算法，将夏普比率作为投资组合绩效的评估函数，采用相同的惩罚函数。采用公式2.9 和公式2.10 更新粒子的速度和位置，并根据夏普比率确定每个粒子的个体极值，如果新位置的夏普比率高于个体极值，则个体极值更新为新位置的值，否则保持个体极值不变。再确定粒子的全局最优值，如果所有粒子中的最大夏普比率高于历史最优值，则全局最优值更新为新位置的值，否则保持全局最优值不变。因此得到全局最优值的个体，计算投资组合模型的收益率和风险，重复迭代，将粒子群收敛到全局最优值，设置迭代次数为4，满足迭代次数后退出算法。表5 表示基于矩阵值因子算法的均值-方差优化模型在不同期望收益率情况下的粒子群算法求解得到的最好方差、均值方差和均值收益率。

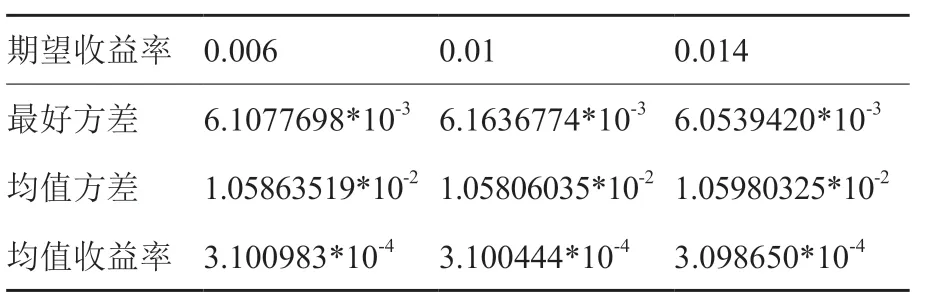
表5 基于矩阵值因子算法的均值-方差优化模型的粒子群算法求解Table 5 Particle swarm optimization for solving the meanvariance optimization model based on matrix-valued factor algorithm

2.4.4 实验结果对比分析

通过对比基于矩阵值因子算法的均值-方差优化模型的CVXOPT 求解器、遗传算法求解和粒子群算法求解的三模型结果，如表6、7、8 所示，在达到相同期望收益率时，基于遗传算法的投资组合模型具有更小的最好方差和均值方差，方差是用来度量投资组合的风险，因此也代表该组合的波动率更低，在达到相同收益率的情况下，采用遗传算法构建的投资组合模型的风险更小，符合企业年金的安全性原则。在均值收益率方面可以看出，遗传算法和CVXOPT 求解器两种模型所得的均值收益率在不同期望收益率下均高于粒子群算法。因此，综合最好方差、均值方差和均值收益率三个指标，本文选用遗传算法求解企业年金的均值-方差优化模型，并对该模型进行并行计算，以解决在实际应用中资产数量过多时，资产规模过大导致模型无法在有效时间内求得最优解且解质量不高的问题，更快的找到全局最优解。

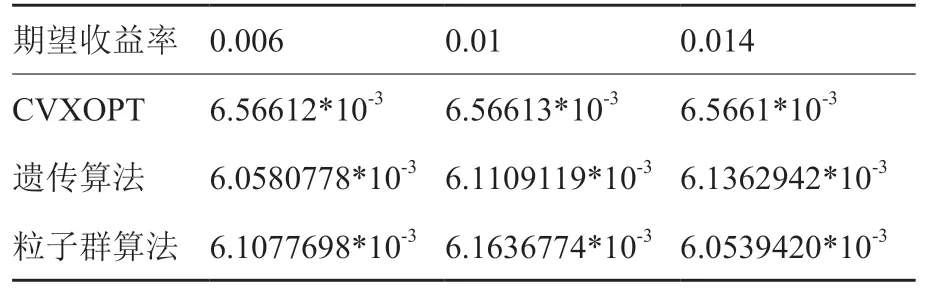
表6 最好方差Table 6 Best variance

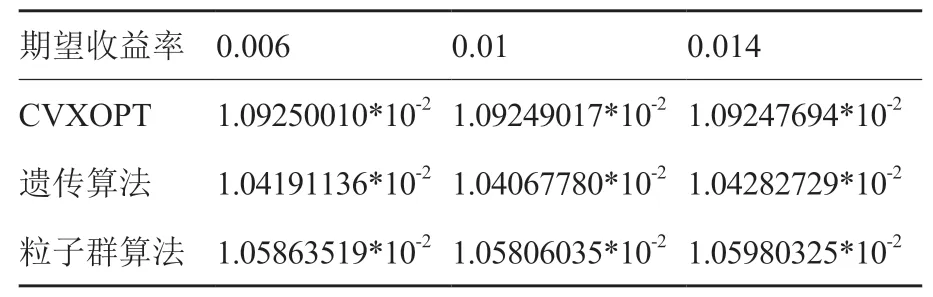
表7 均值方差Table 7 Mean variance

表8 均值收益率Table 8 Mean return

2.5 均值-方差优化模型的矩阵值因子算法和遗传算法并行化的实验结果

（1）运行时间

本文统计了取期望收益率为0.01 时，在处理器核数分别为1、2、4、6 和8 核的情况下，并行算法在不同处理器核上的运行时间。其中，运行时间是取值程序的并行算法部分，从开始到最后一个进程结束所需要的时间，如图4 所示。

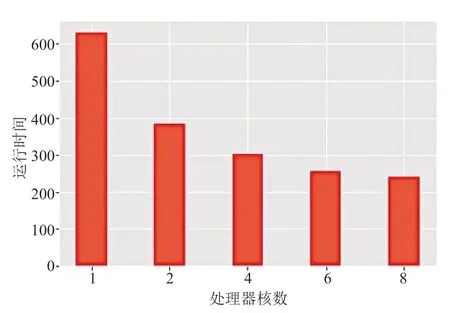
图4 不同处理器核数上的运行时间Fig.4 Running time on different processor cores

可以看出，随着并发线程的数目的增多，算法的运行时间越短，并行加速效果明显，优化的模型可以有效缩短求解时间。

（2）加速比

加速比定义了性能优化的效果，取值为最佳串行算法所需的运行时间与多个并行处理器所需的运行时间之比。如图5 所示，当模型使用2、4、6、8个线程并发计算时，运行时间是基准模型的1.6422、2.0759、2.4474 和2.6099 倍，表明该模型并行计算后效率显著提升。

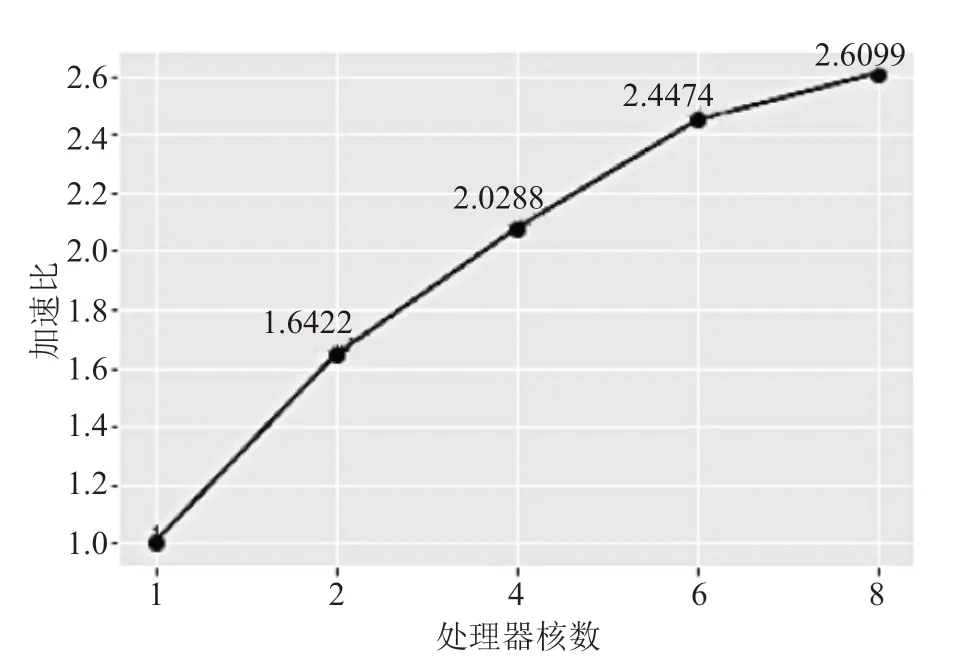
图5 不同处理器核数上的加速比Fig.5 Speedup ratio on different processor cores

3 结论与展望

目前没有从投资组合的协方差等各资产相关性角度制定的企业年金的投资策略，因此遵循企业年金的安全性、收益性和流通性的原则，本文从协方差矩阵方面进行企业年金的投资组合模型研究。为了适应企业年金的实际操作需要，本文对传统均值-方差模型进行改进，使用Python 语言实现了基于矩阵值因子算法的带投资约束条件的均值-方差优化模型，可以对原始高维已实现协方差矩阵进行矩阵值因子分析，探究协方差元素之间的相关性联系。同时，该模型基于Cholesky 分解和向量自回归的方法，有效的建模和预测了矩阵值因子模型，缓解了在资产数量过多的情况下，高维协方差矩阵的运算量大不易求解的问题，并可基于时间序列数据中资产的协方差矩阵来预测未来的风险度量以及资产相关性的变化情况。此外，该投资组合优化模型归类为二次规划问题，为了能有效求解该二次规划模型，本文实现了基于CVXOPT 求解器、遗传算法和粒子群算法三种求解方法，并将三种求解方法的结果进行对比，分别衡量在不同预期收益率条件下资产配置的模型性能，结果表明在达到相同期望收益率时，基于遗传算法的投资组合模型具有更小的风险，因此本文选用遗传算法求解企业年金的均值-方差优化模型，并对该模型进行并行计算，以解决在实际应用中资产数量过多时，资产规模过大导致模型无法在有效时间内求得最优解且解质量不高的问题。结果表明，通过并行计算该模型的计算效率显著提升，可有效缩短模型运行时间。

虽然本文实现了面向企业年金的基于矩阵值因子算法的均值方差优化模型，但仍存在一些不足，需要进一步的研究和改进，比如Markowitz 均值方差模型要求输入资产间的方差、期望收益率和相关系数，一旦数据存在误差会产生解的不可靠性，资产权重会因为输入数据的很小改变而产生很大的变化，从而影响解的质量。此外，可以对年金计划职工的风险承受能力进行区分，因为企业在选择企业年金的投资组合时，通常统一将所有资金投资于某一种或几种投资组合，而并没有考虑职工的风险承受能力的差别，这样也降低了投资组合的收益率。

利益冲突声明

所有作者声明不存在利益冲突关系。