基于AutoML的湍流建模

任荟颖, 王婧, 王彦棡*

1.中国科学院计算机网络信息中心, 北京 100190

2.中国科学院大学, 北京 100049

引 言

在过去的十年中，随着计算机硬件的不断发展，CFD(Computational Fluid Dynamics)已经成为用于流体分析的更主要的工具。目前，对复杂流体力学系统进行建模主要有两种途径。第一种是基于理论的模型架构，即根据物理问题的控制方程，建立理想的系统描述；第二种则是目前比较流行的数据驱动方法[1-2]，即根据系统仿真或试验中的样本数据，直接构造黑箱或灰箱模型。近年来，随着计算机性能和精细化流动测试手段的发展，研究者能够获得高精度、高时空分辨率的流场信息。如何高效地利用这些大数据，从中提取出关键信息，并指导流体力学的发展，已经成为研究者关注的焦点。作为处理和分析数据的主要手段，数据挖掘、统计学习和机器学习等技术，则为开展此类研究提供了重要基础[3]。

雷诺时均Navier-Stokes(RANS)方程[4]提供了一种计算时间平均湍流量的有效方法，由于其计算易处理性而被广泛使用。目前，RANS 模型在实际生产和工程中仍占有重要地位。而在RANS 计算的过程中，能否准确求解雷诺应力至关重要。近些年来，人们开始关注使用机器学习和深度方法来求解RANS 方程。Tracey 等人[5]使用核回归来模拟雷诺应力各向异性特征值。该方法被证明在大量训练数据上的应用效果较差。Tracey，Duraisamy 和Alonso[6]后来使用具有单个隐藏层的神经网络来模拟Spalart Allmaras 模型中的源项。实验证明这些神经网络能够重建这些源项。 Ma，Lu 和Tryggvason[7]使用神经网络代替流体闭合方程来模拟等温气泡流。Zhang 和Duraisamy[8]使用神经网络来预测湍流产生项的修正因子。该修正因子会影响预测的雷诺应力张量的幅度但不影响其各向异性。 Ling J，Ruiz A 和Lacaze G[9]等人提出使用随机森林来预测雷诺应力各向异性。该方法被证明不能轻易地对张量数量强制执行伽利略不变性，因此在预测完全各向异性张量方面的能力有限。Ling J，Kurzawski A 和Templeton J[10]提出一种新的深度神经网络结构从高保真仿真数据中学习雷诺应力各向异性张量，并且他们展示了基于深度学习的雷诺应力对不同几何形状的流动的预测能力。这种方法被证明对DNS 仿真效果不好，并且只针对于定常流动。Kutz[11]解决了基于DL 的闭合方程应用的几个开放性挑战，解决了应该选择怎样的训练数据的问题。Chang 和Dinh[12]分析了五种类型的机器学习框架，讨论了如何耦合机器学习框架和流体模拟的问题。Chang 和Dinh[13]后来采用了深度学习的方法来拟合雷诺应力。这种方法被证明对于非定常流动的效果拟合较差，无法拟合出精确的流场效果。

近些年来，自动机器学习技术(Auto Machine Learning，AutoML)有了长足的突破和发展。在深度学习领域，自动机器学习技术包含自动调节超参 数[14-15](例如学习率)、自动调整网络结构[16-17](例如神经元的个数，层数等)，在深度学习领域取得了不错的成绩。由于在湍流问题中，不同的系统初始条件不同，数据的质量千差万别，难以使用统一的神经网络进行训练。因此用深度学习中AutoML 的方法进行拟合，针对不同的数据集自动选取不同的网络结构和参数。此外本文还通过混合多种初始条件下的数据进行模型的训练来提高拟合的精度和模型的鲁棒性。实验表明，拟合效果较之前的方法有了较大程度的提升。

1 相关理论及方法

1.1 AutoML 贝叶斯优化理论

机器学习中，调参和搜索网络结构被认为是一项繁琐且耗费人力的工作。手动调参十分耗时，参数的好坏影响网络的性能。 网格和随机搜索需要很长的运行时间，因此诞生了很多自动调参的方法。 长期以来，高斯过程一直被认为是一种针对模型的建模损失函数的好方法[18]。高斯过程(GPs[19])具体描述为建立目标函数的概率模型，用它来选择效果最好的超参数，在真实的目标函数中进行评价。

超参数优化的过程可以描述为：

这里(xf)表示在验证集上评估得出的最低损失函数的值(例如，RMSE 或错误率)；x*是产生该最低值的超参数集，并且x可以在超参数域χ中取任意值。简单来说，我们想找到在验证集度量标准上产生最佳分数的超参数集合。

高斯过程通过观察过去的评估结果，计算超参数映射到目标函数得分概率的概率模型：

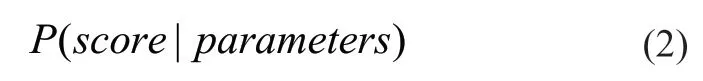
此函数被称为目标函数的“代理”。高斯过程方法通过选择最有潜力的超参数组，通过目标函数进行评估，再带入到高斯过程模型中，进而选择下一组超参数，反复迭代。

具体的算法过程可以描述如下：

(1)建立高斯函数模型M，假设损失函数f的输出值y与超参数x之间的关系服从M；

(2)从M中采集下一组函数值较高的参数x1+t；

(3)将x1+t带入到损失函数f并计算出分数y1+t；

(4)将x1+t和y1+t更新到M中；

(5)重复步骤(1)到(4)直到满足停止条件。

贝叶斯优化方法在理论上是有效的，因为它以有根据的方式选择了下一个超参数。它的基本思想是：花更多的时间选择下一个超参数，以减少对目标函数的调用。实际上，与在目标函数中评估花费的时间相比，选择下一个超参数所花费的时间是很少甚至无关紧要的。通过评估，从过去的结果选取出看似更有希望的超参数，贝叶斯方法可以在更少的迭代中找到比随机搜索更好的模型参数设置。

1.2 深度学习在湍流模拟中的应用方法

机器学习与湍流建模相结合的研究工作是流体力学领域新兴的热门研究方向。现有的研究成果有力地验证了其有效性和可行性，预示了机器学习在未来湍流模型应用中良好的应用前景[20]。一方面，这些研究工作以数值模拟器或实验产生的高分辨率的数据作为驱动，一定程度上降低了机器学习模型封闭或湍流模型相关变量模型化的难度，证实了纯数据驱动的机器学习黑箱模型在湍流研究应用中的有效性和可行性。另一方面，一些研究者还将机器学习用于描述和量化传统模型计算结果的不确定度，对未来的建模工作具有很好的指导作用[21]。主要的研究方向和建模流程归结为图1所示。

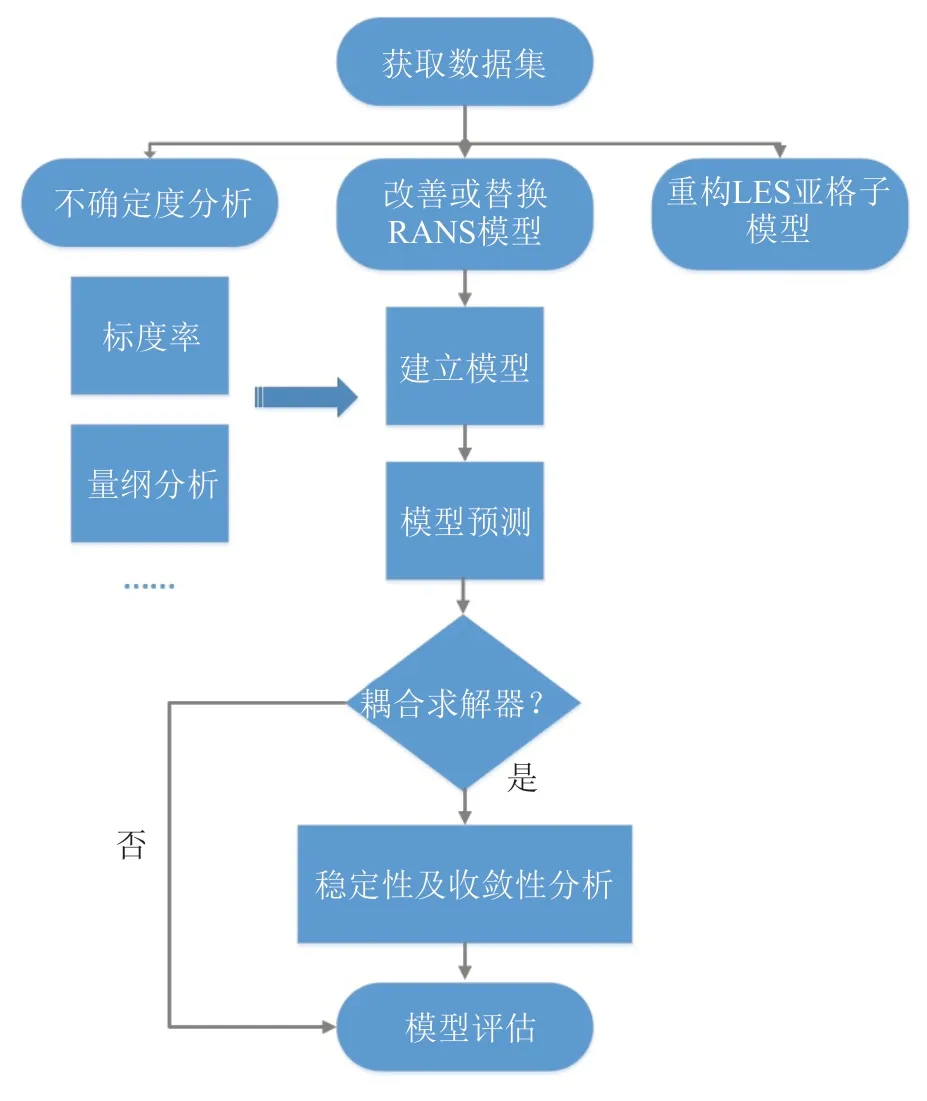
图1 机器学习应用于湍流研究的主要研究方向及流程Fig.1 Main research direction and process of machine learning applied to turbulence study

2 本文方法

2.1 RANS-DL 模型

我们假设深度学习可以从不同流场区域中采集的速度场中发现隐藏的时间导数[13]。因此，我们可以从各种模拟时间步骤中采样数据，并使用总数据训练神经网络。因为深度学习属于监督学习方法，需要输入和输出来训练模型。因此，对于深度学习湍流模型，输入应该是能表示平均流动特性的流动特征，目标为雷诺应力六个分量。我们基于RANS方程[22]选择输入的流动特征。RANS 方程推导输入输出的过程如下所示：

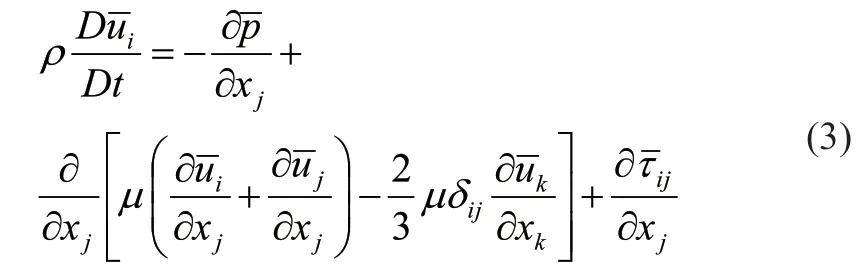
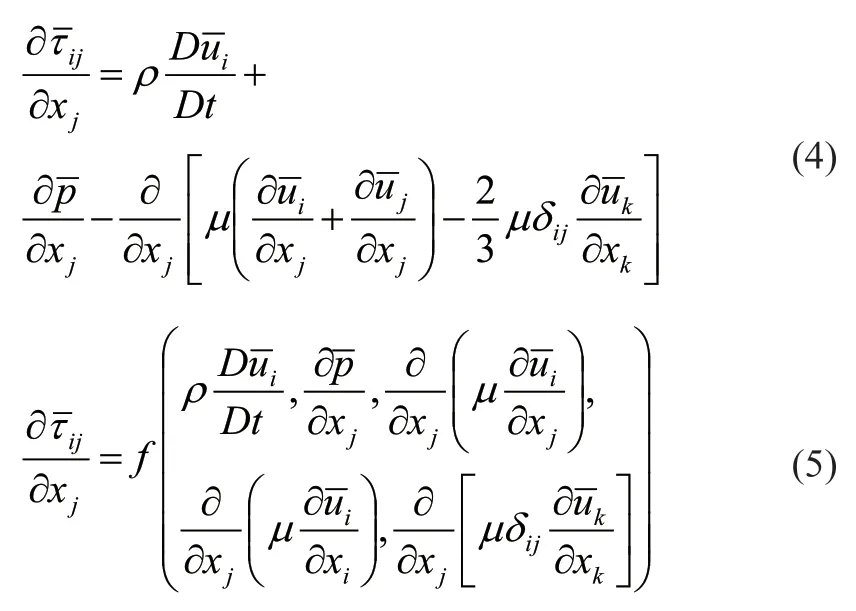
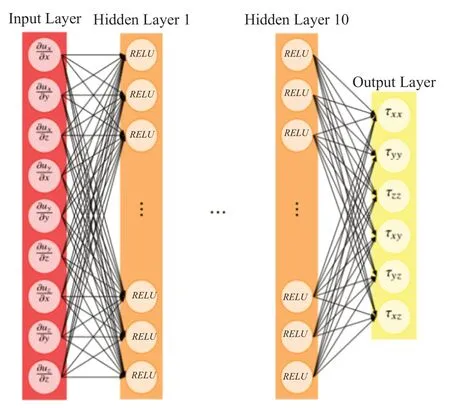
图2 RANS-DL 模型Fig.2 RANS-DL model

这里是平均速度，i，j，k是方向，ρ，，τij，µ和分别为流体密度，平均压力，雷诺应力分量，粘性系数和Kronecker delta 函数。基于我们的假设，每个数据集的数据稳定，因此不选择时间导数作为训练输入。而压力是从动量方程中单独求解的，因此我们进一步发现压力项可以从训练输入中排除。因此基于深度学习的湍流模型的输入可以通过速度的空间导数来表示。使用矩阵形式显示雷诺应力与导数算子、速度的之间的二元乘积，具有的函数关系如公式(6)所示：

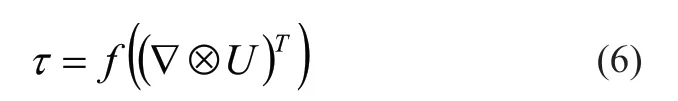
由于DNN 能够较好的解决回归问题，我们使用DNN 来回归拟合替雷诺应力。损失函数采用欧几里德损失函数，其中，分别为训练数据的总数，训练结果和雷诺应力值，如公式(7)所示：

图2 为模型的具体形式，只采用每个点的9 个速度导数作为输入流特征，目标是它的六个雷诺应力分量。

2.2 RANS-DL 工作流程

我们假设闭包关系可以从守恒方程实验数据和数据驱动的机器学习模型中分别导出。如图3 所示，RANS-DL 工作流具体描述如下：

(1)首先定义了某一问题的物理几何边界，如模拟结构和系统特性；

(2)利用该几何边界构造了CFD 计算实例，包括初始条件、边界条件等；

(3) CFD 求解器执行模拟；

(4)从模拟中提取和处理相关数据；

(5)使用这些处理后的数据来训练神经网络。

2.3 RANS-AutoML 模型

本文采用了基于AutoML 的技术，能够根据不同的初始条件的数据集自动设计网络结构以及调整参数。本文采取贝叶斯优化器负责自动构建网络模型结构（例如RANS-DL 模型中隐藏层的节点数，隐藏层的层数），以及自动搜索模型的参数（例如RANS-DL 模型中的学习率，学习率衰减指数以及L2 正则系数）。 贝叶斯优化器需要先用随机搜索训练n 个网络，观察n 个网络的性能，从这些过去的经验中更新优化器。主要流程和思想如图4所示。

具体的流程如下：

(1)利用随机搜索获得n 个网络结构和MSE；

(2)从旧的模型结构，参数以及MSE 值生成下一轮需要搜索的模型结构和参数用于模型训练；

(3)模型训练，在验证集上验证产生MSE 值；

(4)将本轮的模型结构和参数以及得到的MSE的值再反馈到贝叶斯优化器中；

(5) 重复步骤(1)～(4)直到达到搜索时间或者搜索网络结构得到的MSE 值达到预期，便结束得到最优网络的结构及参数。

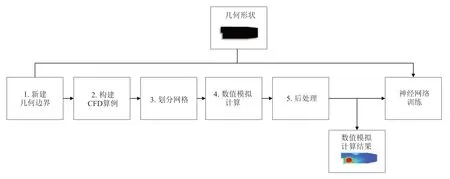
图3 RANS-DL 工作流程Fig.3 RANS-DL workflow

图4 AutoML 工作流程Fig.4 AutoML workflow

3 实验设置

3.1 数值实验

进行数值实验来产生深度学习模拟雷诺应力需要的数据。采用k-ε模型求解RANS 模拟得到参考解，用于模型的训练。图5 描绘了Pitz 和Daily[23]提出的内壁形状，这是一个2D 的几何形状，包括一个向后的台阶和一个喷嘴。系统特性总结在表1 中。由于不稳定的流动受到湍流混合层、剪切速率等的影响，因此这种几何形状足够复杂。对于这种几何形状，k-ε模型已被验证是可行的[24]。我们用OpenFOAM[25]中的pimpleFoam 求解器用于生成数据。

使用k-ε模型通过RANS 仿真生成训练数据。 采用pimpleFoam 求解方程，固定时间步长5×10-10秒。为了观察不同的系统初始条件对实验结果的影响，我们设计了8 个数据集，并在表2 中列出。设计实验如下：

(1)采用A1、A2、A3 分别训练，并在验证集B上验证观察实验结果，观测对训练数据进行时间和空间的加密对测试结果有无影响；

(2)采用A1、A4、A5/A1、A6、A7 分别/混合训练，并在验证集B 上验证观察实验结果，观测改变训练数据的入口流速/层流粘性系数对测试结果有无影响；

(3)采用A1、A6、A7 分别/混合训练，并在验证集B 上验证观察实验结果，观测改变训练数据的层流粘性系数对测试结果有无影响。

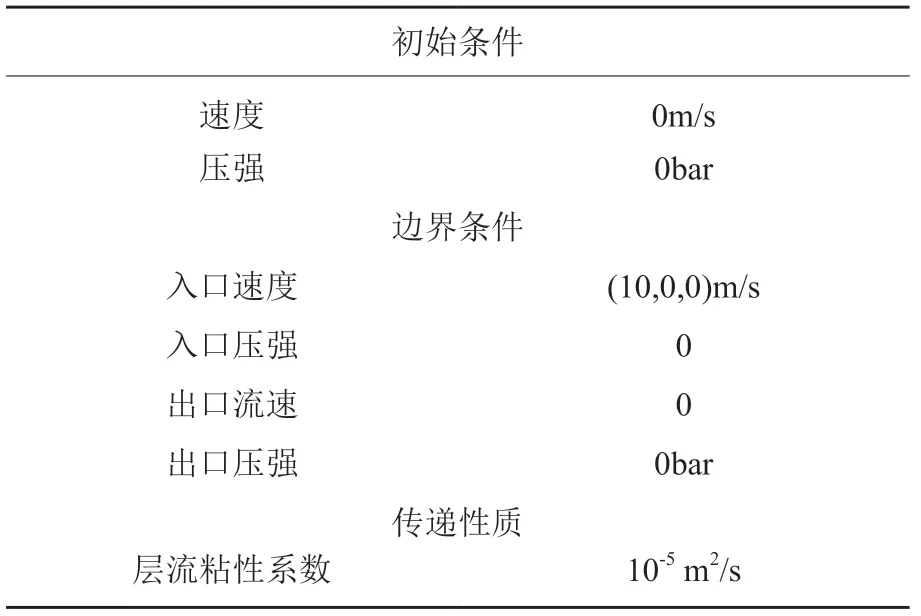
表1 系统边界信息Table 1 System boundary information

3.2 基于AutoML 的雷诺平均湍流模型求解模型

图5 数值模拟实验信息Fig.5 Experimental information of numerical simulation

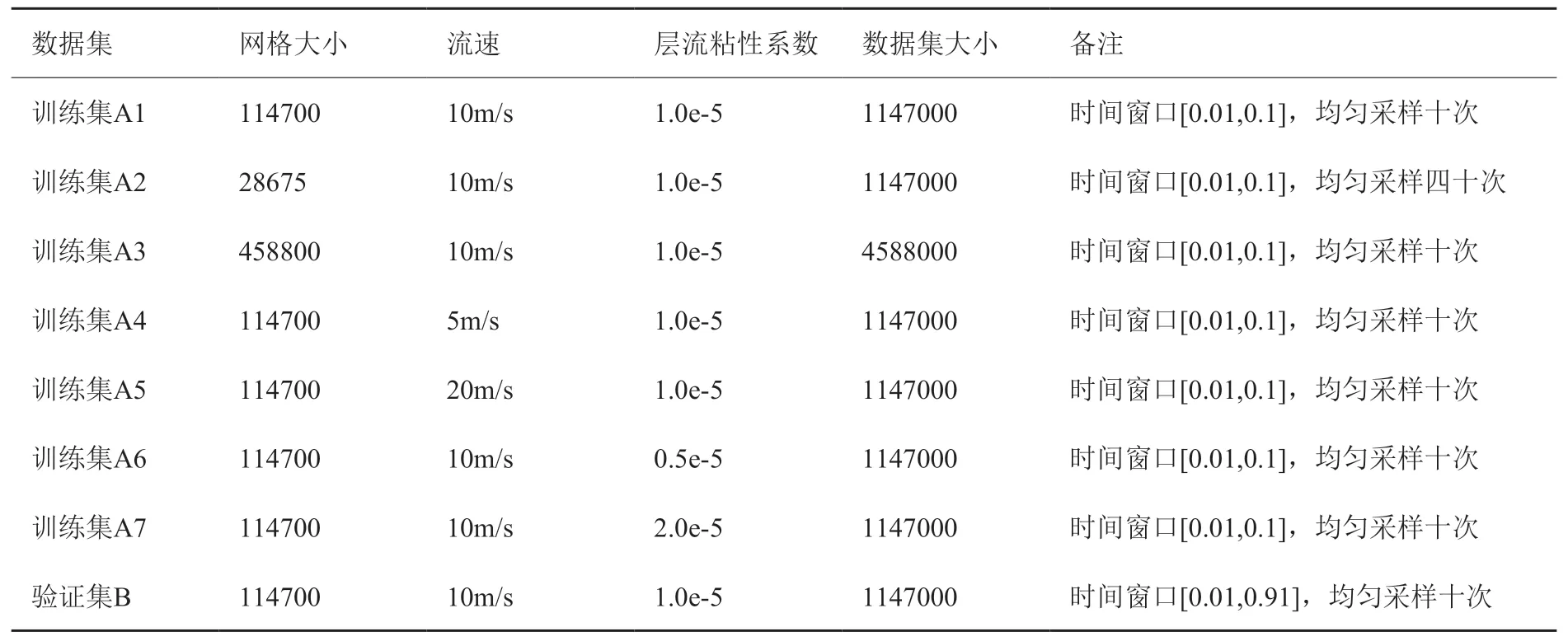
表2 数据集信息Table 2 Dataset information

我们使用Tensorflow[26]来设计DNN 结构，激活函数采用ReLU[27]，并且在每个隐藏层采用BN[28]。 模型采用Adam[29]算法作为深度学习的优化算法来更新模型的参数，例如权重w和偏差b等。模型的网络结果和具体参数，包含：网络的层数，每层隐藏单元的个数、学习率、L2 正则系数均用前文介绍的贝叶斯优化方法进行搜索。

4 实验结果及分析

为了更好的展示实验的结果，如图5 所示，我们选取了验证集上流场的不同区域来观察模型训练的效果。这些区域包含入口，台阶流，流场中较为平缓的区域以及出口处的区域，比较能代表流场的情况，从而反应出模型训练的效果。

4.1 AutoML 实验结果

网络结构搜索以及参数调整的小时数为48 小时，本文做实验的机器配置：CPU 为双核4 线程， GPU 为Tesla V100。最终AutoML 的训练效果如图6 所示。经过训练，本文最终采用的模型参数如表3所示。

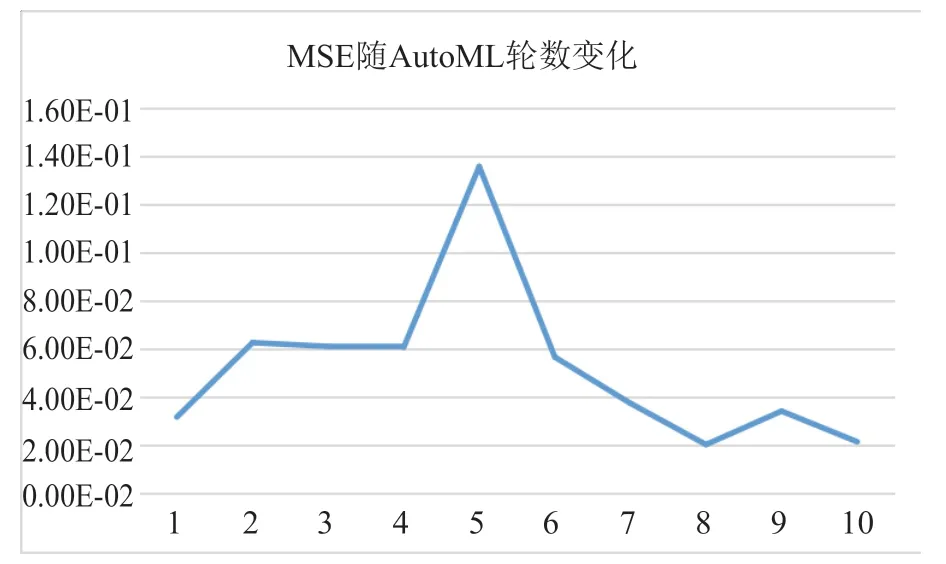
图6 AutoML 的效果Fig.6 Effect of AutoML model

表3 模型参数Table 3 model parameter

如图7 所示，与Chang 和Dinh[10]采用的神经网络结构来拟合雷诺应力的效果对比，我们用AutoML 获得的网络结构拟合效果更为优异。

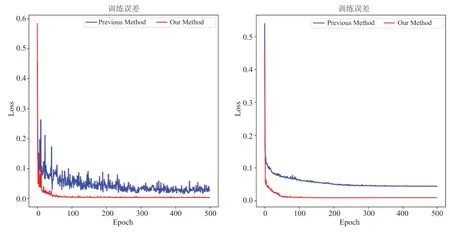
图7 AutoML 的网络结构与之前方法的对比Fig.7 Comparison between AutoML network structure and previous methods

4.2 时间信息对模型的影响

我们假设深度学习可以从不同流场区域中采集的速度场中发现隐藏的时间导数，因此需要验证训练好的模型能否重建验证集上的不同时刻的雷诺应力的参考解。 如图8 所示，在模拟过程中，每个雷诺应力张量分量的MSE 随时间保持稳定。因此可以得出结论，DNN 模型可以学习到流场数据中隐含的时间导数信息。

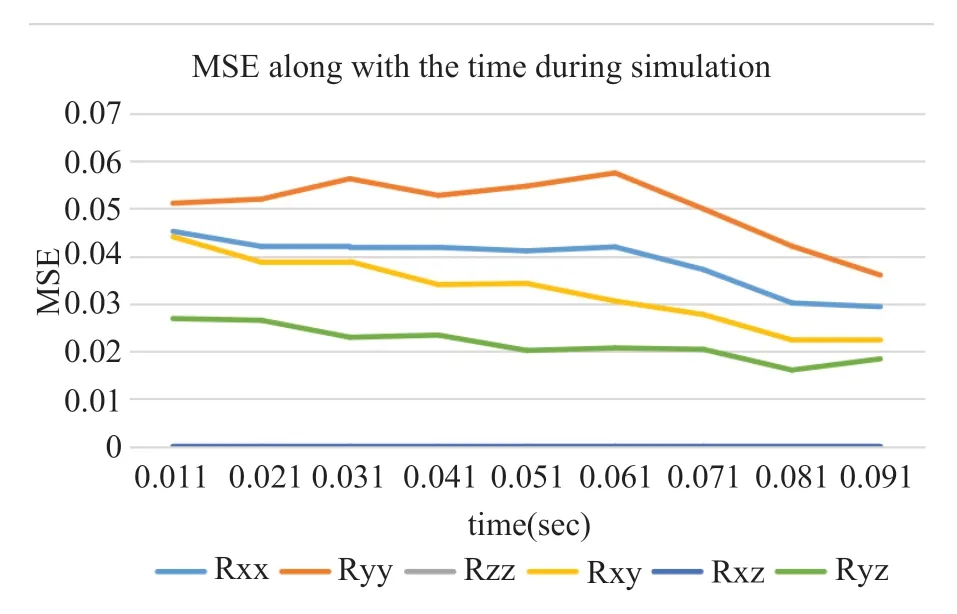
图8 雷诺应力张量分量随时间变化拟合效果Fig.8 MSE along with the time during simulation

4.3 网格疏密对模型的影响

为了检验数值实验中网格的疏密对深度学习网络模型的训练效果有无影响，我们将模型分别以四倍的网格差在不同疏密程度的数据上进行训练，同时为了降低数据规模变化对模型训练造成的影响，将稀疏网格的数据在时间采样上加密了四倍，在验证集上进行验证。如图9 所示，从粗网格生成的训练数据的训练结果与从细网格生成的数据训练结果几乎相同。

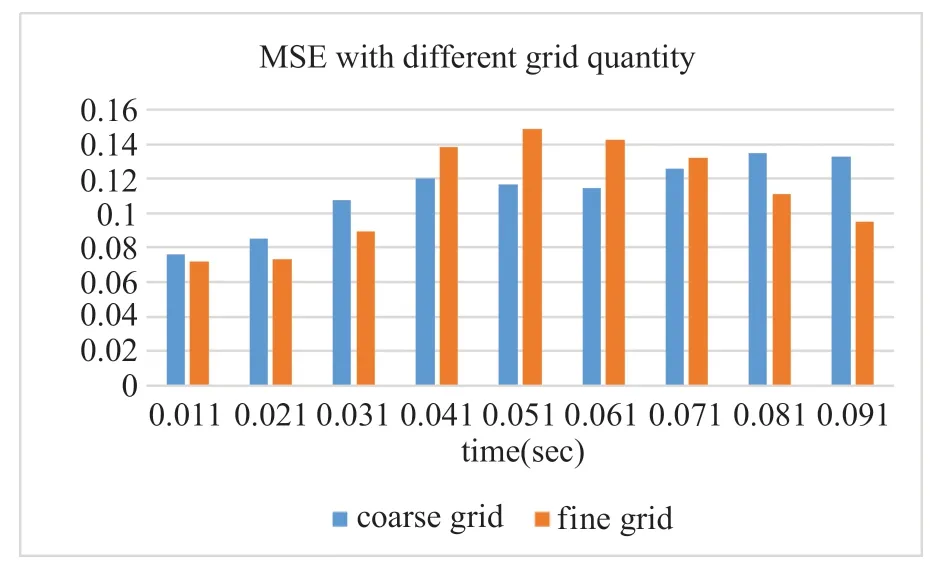
图9 不同疏密网格数据训练模型的效果Fig.9 MSE with different grid quantity

4.4 扰动入口流速对模型的影响

为了检验入口流速的改变是否会对模型的训练结果造成影响，将模型分别在入口流速为5m/s、20m/s 以及混合多种流速的情况下进行训练，并在验证集上进行验证。如图10 所示，模型在较小的入口流速下训练模型，会倾向于预测较小的结果；模型在较大的入口流速下训练模型，预测的结果也会偏大；而在混合入口流速下，训练的效果更好，模型的鲁棒性也更好。

4.5 扰动层流粘性系数对模型的影响

为了检验层流粘性系数的改变是否会对模型的训练结果造成影响，将模型分别在层流粘性系数为 0.5e-5m/s、1e-5m/s、2e-5m/s 以及混合多种层流粘性系数的情况下进行训练，并在验证集上进行验证。如图11 所示，模型在较小的层流粘性系数下训练模型，会倾向于预测较大的结果；模型在较大的层流粘性系数下训练模型，预测的结果会偏小；而在混合层流粘性系数下，训练的效果更好，模型的鲁棒性也更好。

5 结论与展望

本文提出了一种用AutoML 方法建模RANS 模型 的方法，该方法使用AutoML 方法来再现RANS(k-ε) 数值模拟的解。通过实验结果的分析, 可以看出基于 AutoML 的方法能够自动构建网络结构和调整参数, 在保证准确率的情况下减少人力的工作。另外，本文还发现了一些有意义的结论：速度场的一阶空间导数的流动特征对于重建RANS 结果是必要且充分的，模型能学到流场数据中隐含的时间导数信息；另外，在混合入口流速、层流粘性系数的数据上训练，能使得模型的鲁棒性更好. 目前，系统的针对湍流机器学习的特征选取的研究还相对较少。在现有工作积累的经验基础上，机器学习在未来的湍流模型化中必将扮演着更加重要的角色。

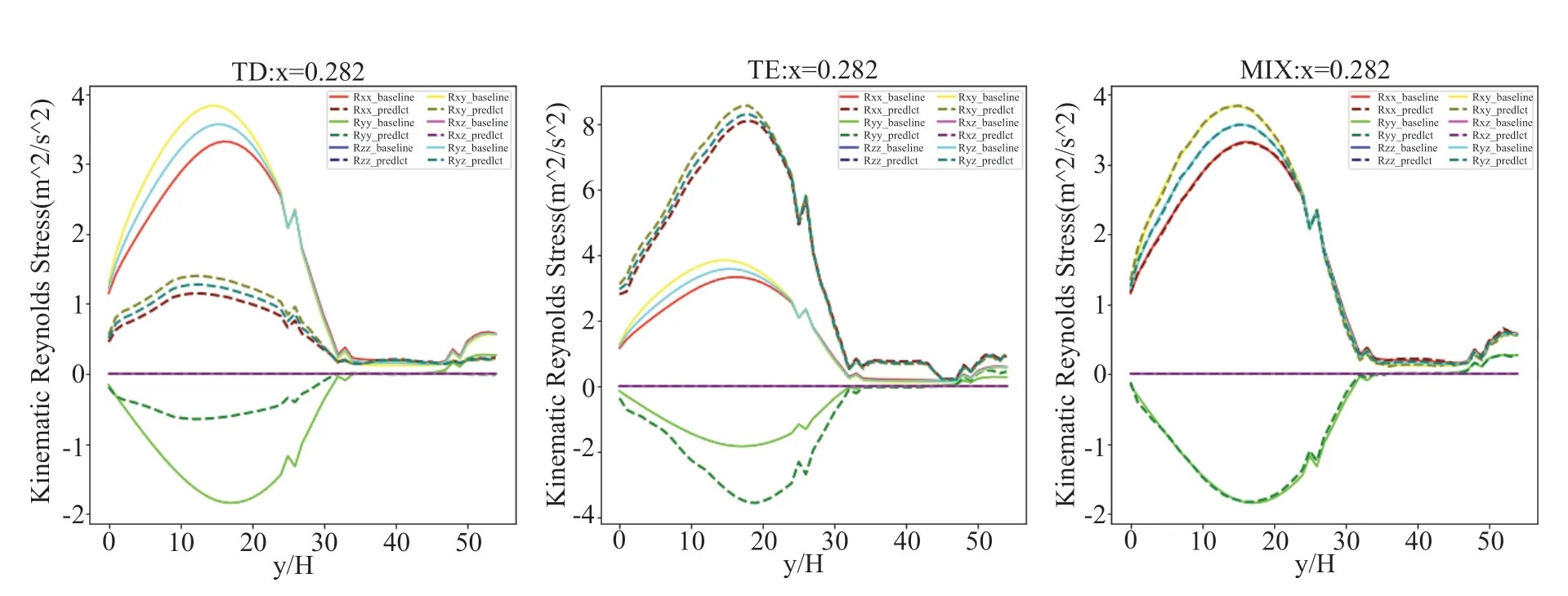
图10 不同入口流速下数据训练模型的效果Fig.10 The effect of data training model under different inlet velocity

图11 不同层流粘性系数下数据训练模型的效果Fig.11 The effect of data training model under different laminar viscosity coefficient

利益冲突声明

所有作者声明不存在利益冲突关系。