小世界银行网络、非线性效应和 尾部风险：随机动态视角

王 鹏 王小军 邵思远

一、引 言

十九大报告强调：“健全金融监管体系，守住不发生系统性金融风险的底线。”防范和化解重大风险是决胜全面建成小康社会三大攻坚战的重要战役。因此，系统性金融风险问题已经上升到了国家安全战略的高度。

一个不容忽视的事实是，近二十年来全球范围内金融业发展非常迅速，金融工具日新月异，金融创新层出不穷，金融与信息技术的融合深度前所未有，这就导致了金融风险比以往任何时候种类都要多、规模都要大。一方面是因为金融监管较之前宽松，金融业竞争加剧，各国金融业间相互关联程度加深，另一方面也是因为支持业务背后的技术手段的进步。以互联网技术为代表的一系列高新技术席卷全球，极大地推动了经济增长，带来了人们生产、生活方式的深刻变革，特别是金融科技(FinTech)的蓬勃发展无形之中增加了金融风险源头。

综合以上国内和国际的经济发展形势，不难看出系统性风险对中国经济而言虽无近忧，但有远虑，开展相应研究的重要性不言而喻。

由于系统性风险的来源、成因比较复杂，同时众多的研究者学术背景各异，这就形成了对这个问题研究视角上的差异。概括起来，主要有两大研究视角：1.从以银行为主的金融机构的日常实际经营业务出发，以资产负债表、同业拆借资金关系等为主要实证数据来源，利用银行相互间的资产-负债关系建立复杂网络(Complex Networks)模型，在此基础上开展后续工作；2.从参与支付系统的金融机构(主要是银行)之间的支付、结算、清算业务出发，以相关的基于支付结算指令的资金转移数据为主要的实证数据来源，把参与机构抽象化为一个简单的资金收付单位(也有一些文献采用异质化处理方式，赋予这些单位学习、决策的能力)，对各银行的财务状况关注比较少，但是把实际的支付计算机制、过程纳入到了模型中。不难看出，这两个视角同时也是系统性风险传导的两种渠道。从目前的情况看，第1 类研究的成果数量要远远多于第2 类研究，或者说对后者的研究是有所不足的。这也是本文选择其作为切入视角的重要原因。

另外，虽然研究对象一致，但由于研究视角的差异，导致第1 类研究和第2 类研究有比较大的差别。首先是一些研究的细节，比如风险的成因。在第1 类研究中，更多考虑的是由信用风险引起的系统性风险，即银行因为相互持有资产/负债或者债权/债务等关系结成一个复杂网络，如果网络中某一个或者几个银行违约，就有可能导致系统性风险事件的发生。再看第2 类研究，从20 世纪90 年代以来，世界上多数国家普遍放弃DNS(延迟差额结算)支付系统而采用RTGS(实时全额结算)系统(两者的联系和区别在后面第三部分有详细阐述)，由于要求支付指令实时完成，因此在支付系统中就不存在信用风险，于是第2 类研究就把注意力放在了源于流动性风险的系统性风险上。

值得注意的是，还存在一类研究，基于股票市场的数据，采用来自金融工程的方法如CoVaR(条件在险价值)、MES(边际期望损失)、SRISK 等开展研究。这类方法通常是用于对银行的系统重要性进行排序。它最主要的瓶颈是，要求被考察的银行是上市企业，因为实证工作需要运用上市银行的股票价格数据。这样会使得研究范围有一定局限，因为不是所有的银行都是上市企业。特别是在中国，银行在金融业中占有支配性地位，但能够上市的银行只是银行业中的一部分。当然，如果只是考察上市银行这个子集，这一类方法还是非常好的。也存在一种观点，把这类研究称为“全局性系统性风险研究”，而前文的第1、2 类研究则称为“特定来源系统性风险研究”(陈湘鹏等，2018)。

另外，从方法论的角度来看，系统性风险方面的研究已经取得不错的进展，但其采用的模型、方法等方面，还有着进一步完善的空间。从经济学中的模型类型来说，经济学中的模型主要可以分为四类：(1)计量模型；(2)指标模型；(3)算法模型；(4)数理模型。与其他三类模型相比，数理模型具有更为严谨的理论形式，能够更深刻地表现出各个变量之间的关系。从目前研究系统性风险的文献来看，采用算法模型、指标模型和计量模型的研究成果占绝大多数，鲜有以数理模型特别是动态的数理模型的形式进行研究而呈现出来的成果。完整的系统性风险理论无疑是需要数理模型的，因此很有必要对此开展研究。特别是针对已经作出的大量实证工作，在理论上以数理模型的形式进行必要的总结、提升就有着比较显著的意义。本文就是对这方面努力作出的一种探索，以求抛砖引玉。

概括来讲，本文的创新之处主要有如下三点：第一，对银行间复杂网络中系统性风险演化开展建模工作，提出用随机NWMY 方程对其进行刻画，并且推导出风险的概率分布满足的Fokker-Planck 方程；第二，运用对方程代数结构具有良好保真性能的代数动力学解法，求得风险的概率分布的近似解析解；第三，考察了系统性风险及其概率分布的时变规律和影响因素，提出了科学的监管在其中的重要作用，仿真工作显示出了银行间网络中的非线性效应对风险的吸收、抑制作用。

二、文献述评

就现有的系统性风险研究文献来看，按照实证工作所采用数据来源的不同，可以分为三类。第1 类使用的数据主要来自金融机构的资产负债表，主要的研究对象是银行系统(Diamond 等，1983；Allen 等，2000；Furfine，2003；马君潞等，2007)，也有扩大到整个国民经济(Merton 等，2007；宫晓琳等，2010；范小云等，2013)的成果，这类研究关注的重点是风险的测度、传染等问题。在以CoVaR 为代表的一类方法兴起之后，针对上市银行群体，出现了第2 类研究，即采用上市银行的股价作为实证数据，运用来自金融工程的方法，如CoVaR(Adrian 等，2011；李志辉等，2011；高国华等，2011；周爱民等，2017)、MES(Marginal Expected Shortfall，Acharya 等，2010；范小云等，2011)、CoES(李政等，2019)、SRISK(Brownlees 等，2012；方意等，2012)等，计算出系统中每个机构的风险值或相互之间的风险排名。不难看出，研究的范围是上市银行这个子集。当然，也有利用其他金融市场数据比如同业拆借市场数据，构建银行间网络模型的研究(左振宇等，2012；欧阳红兵等，2014)。第3 类研究主要采用支付结算数据(Humphrey，1986；Angelini，1996；黄聪等，2010)，比如交易金额、交易笔数等，研究的内容包括对风险的测度、传染等，与第1 类研究的不同之处主要在于更多地考虑了支付系统的结算机制、救助机制等因素对风险的影响。

第1 类研究的优势在于数据易于获取。但是，由于资产负债表数据更新周期较长，数据的连续性不太好，因此与第2、3 类研究相比，第1 类研究的实时性、动态性稍差。第2 类研究采用股价数据，解决了数据连续性差的问题，但由于不是所有的银行都是上市企业，因此研究范围有局限，不能把所有的银行都包括进去，研究结果的说服力稍显不足。另外，这类研究还有着基本没有考虑银行的实际业务、不能考察风险传染路径等不足之处。第3类研究采用的是来自支付系统的数据，系统中的现代信息技术可以使每一笔交易、每一个细节都被实时、完整地记录下来，因此数据的实时性、连续性较好，可以实现对研究中一些指标的实时监测。同时因为所有的银行都会直接或间接通过支付系统开展业务，所以基本可以涵盖所有的银行。其不足之处是由于金融安全的原因，数据的可获取性较差，但近年来此领域研究普遍采用的真实数据与仿真数据结合的办法，可以较好地解决这个问题(Docherty 等，2010；王鹏等，2014)。

从支付系统的角度研究系统性风险问题，主要是以Diamond 和Dybvig(1983)提出的三阶段模型为起点，该模型也就是通常所说的D-D 模型(银行挤兑模型)。Allen和Gale(2000)在D-D 模型的研究基础上提出了一个网络(Networks)传染模型。在模型中区域流动性冲击是异质的，但是流动性总需求固定。他们的研究表明，不同网络结构，对风险的抵御能力是不一样的。由于在研究中，采用了基于图论(Graph Theory)的模型(也可以称之为网络模型)，比较了不同图(网络)结构的风险的不同，被后继者认为是基于复杂网络理论研究的真正意义上的开端。更多考虑了支付结算的细节，开创性地研究 CHIPS(纽约清算所银行同业支付系统)中的系统性风险问题的是Humphrey(1986)。他认为系统性风险是真实存在的威胁，采用计算机模拟方法的研究结果表明，当系统中一个主要参与者违约时，其他参与者多有可能会违约。由于支付系统中没有担保机制，如果拥有最大债务的参与者违约，将会在系统中导致严重的风险传染。在Humphrey 工作的基础上，Angelini 等(1996)采用了Humphrey 的方法，对意大利大额支付系统做了仿真研究，另外讨论了意大利系统和CHIPS 在结构上的差异。随后，Bech 等(2002)和Northcott(2002)采用同样的方法分别对丹麦和加拿大的支付系统开展了研究。

以上研究，虽然实际上都使用了网络模型，但是都没有鲜明地提出建模是基于复杂网络的。自2008 年金融危机以来，国际货币基金组织(IMF)在《Global Financial Stability Report》(2009)中把复杂网络作为分析系统性风险最主要的标准模型之一，这对于支付系统中系统性风险的研究产生了重要影响。之后出现了非常多的成果，都是有意识地把复杂网络作为建模的主要理论依据。芬兰央行从2005 年至今，每年组织编辑的系列支付经济学研究文集充分体现了这一点。

早期对复杂网络模型的使用仅停留在分析模型的静态几何参数阶段(Boss，2004；Inaoka，2004)，稍复杂一些的研究是建立支付系统复杂网络之后对网络本身的拓扑结构、稳定性的研究(Soramaki 等，2007)，以期加深对支付系统网络结构的理解，但是进一步研究系统性风险测度和传染的成果不多。直到出现Afonso 等(2008)、Docherty 等(2010)、黄聪等(2010)、童牧等(2012)等研究者的工作后，较为明确的研究范式才得以确立，即建立支付系统的网络模型只是一个必要的开端和基础，更多的工作集中在模型建立以后，提出新的统计指标，然后在网络模型上通过仿真模拟考察、对比这些指标来完成风险的测度、传染机制、管理策略等的分析工作。时至今日，这个领域内的大多数研究仍然采用这一模式，即一种基于计算机算法的研究思路。

从上述概述不难看出，以往研究多数采用的是计算机仿真方法即前文提到过的算法模型，且基本上是以基于违约机制经过若干次模拟得到的损失的平均值，来作为系统性风险的测度。这个计算过程反映了研究者通常认为系统性风险是一个随机过程。之所以鲜有文献去探索系统性风险的概率分布问题，是由于算法模型的局限性很难模拟出对应的概率分布，更遑论分布的解析表达式了。本文采用数理模型的思路在这方面做出了一些探索。

三、基于支付结算数据的中国银行间复杂网络及其小世界特征

通常，支付系统是指包含一套支付工具和制度，为系统参与者实现资金转账的系统(中国人民银行，2006)。依据结算机制的不同，支付系统主要分为延迟差额结算(Deferred Net Settlement，简称DNS)系统和实时全额结算(Real Time Gross Settlement，简称RTGS)系统两类。DNS 系统不实时处理每笔支付指令，而是在日间指定的某一个或几个时刻集中处理，只结算轧差之后的净头寸(Net Position)，支付总量相比通常很小，因此整个系统运行需要的流动性(Liquidity)很小。但是这种结算方式存在信用风险。RTGS 系统具有实时、逐笔结算的特性，只要支付指令执行方的流动性充足，实时结算就会顺利进行；如果执行方的流动性额度不够，支付指令则会进入排队序列等待，这样RTGS 系统就避免了信用风险。虽然RTGS 系统中会存在流动性饥渴的问题，但目前还是为多数国家所采用，包括美联储、日本、欧盟等，我国的“中国现代化支付系统”也属此类。综合来看，这两种系统是中央银行在流动性节约和风险两方面的取舍不同的产物。

与许多国家类似，中国现代化支付系统主要由大额实时支付系统(High Value Payment System，简称HVPS)和小额批量支付系统(Bulk Electronic Payment System，简称BEPS)及其他相关系统组成。从交易金额和交易笔数占比上看，占支配地位的还是大额支付系统。这也是大多数研究采用大额支付系统作为本国支付系统代表的原因(Inaoka 等，2004；Soramaki 等，2007)。

由于支付系统的主要参与机构是银行，而支付结算数据代表着银行间的资金往来关系，因此不少文献都基于这类数据建立银行间的复杂网络模型，而且支付系统复杂网络是与银行间复杂网络等价的称谓，后文也将不加区别地使用这两个名称。

首先我们需要根据真实支付结算数据，以参与支付系统的银行为节点(Node)，以它们的资金往来关系为边(Edge)，构建中国支付系统的复杂网络模型，并通过主要参数分析其拓扑特征，为后续研究奠定基础。数据主要来自《中国支付体系发展报告》(2006—2015)和相应银行的年报，同时运用了合成数据(Synthetic Data)估计法(Docherty 和Wang，2010)和最大熵方法(Upper 和Worms，2004)来完成数据细节的 估算。

银行网络可以表示为矩阵的形式，其中每个矩阵元就是两个银行i 和j 之间的资金往来量。设银行间资金往来矩阵为P，该矩阵可以表示如下：

《中国支付体系发展报告》只给出了银行类别(如国有商业银行、股份制银行等)之间的资金往来数据，细节数据需要估算。相关文献(欧阳卫民，2010)给出了国有商业银行以及股份制银行在各自类别中的支付金额比例。本文以此为基础，同时采用了相应银行年报中资产负债表、利润表和现金流量表中的数据，运用合成数据估计法，估算出了各银行和各银行类别之间的资金往来总量。然后，用最大熵方法(Upper 和Worms， 2004)估算最终的银行之间资金往来的具体金额。实际上就是求解以下规划问题：

另外，由于不同年份支付系统中的参与机构有变化，因此按通常的处理办法将重要的机构单独作为一个节点，非重要、数量又有变化的机构作为一类节点来处理。在归类时按照《中国支付体系发展报告》中的分类原则来分类。最终确定网络中共有26个机构或者机构类别(比如外资银行就是一类)。构建的复杂网络的图形见图1。

图1 有26 个节点，是按照《中国支付体系发展报告》中的分类方法，分别代表参与支付系统的26 家(类)银行，包括3 家政策性银行、5 家国有控股股份制银行、12 家股份制商业银行、中国邮政储蓄银行、城市商业银行、农村商业银行、农村信用社、外资银行和其他机构。图1 中边的粗细表现了交易金额的大小。

拓扑特征是描述一个复杂网络的重要手段，小世界性是最为重要的拓扑特征之一。按照定义，一个复杂网络同时具有较小的平均路径长度和较大的聚集系数时，这个网络就具有小世界性。由于本文后面的研究需要判断中国的银行间复杂网络是否具有小世界性，因而就需要计算平均路径长度和聚集系数两个拓扑参数。

图1 中国支付系统网络结构

其中，jC 是节点j 的聚集系数，jE 是节点j 与相邻节点之间实际存在的边数，jk是节点j 的度。全网络的聚集系数C 就是jC 对所有节点的平均值。

根据以上两个公式，经计算得到中国银行间网络的平均路径长度为1.5，聚集系数为0.83。这个计算结果与之前文献(程建平，2012；陆婷婷，2013)中的结果基本一致。在之前文献(Soramaki 等，2007；Becher 等，2008)中，Soramaki 等计算美联储Fedwire系统的平均路径长度和聚集系数分别是2.6 和0.53，结论是Fedwire 系统具有小世界性；Becher 等计算英国CHAPS 系统的平均路径长度和聚集系数分别是2.6 和0.27，结论类似，CHAPS 系统具有小世界性。由于具有更小的平均路径长度和更大的聚集系数，因此可以判断中国的基于支付结算数据的银行间复杂网络具有小世界性。

在社会关系网络中，具有小世界性的含义是系统中任意两个人之间以很大概率有着共同的朋友。我国银行网络的小世界性与此类似，回顾我国银行业发展的历史，从最初的中国人民银行，到专业银行，进而发展成国有商业银行，在这之后才出现了股份制银行、城市/农村商业银行等共同发展的局面。后面发展起来的这些银行，都会与几大国有商业银行有着非常密切的业务联系，类似于社会网络中有着共同“朋友”的情况。银行业发展的历史沿革，显然是导致我国银行网络有着小世界性的重要原因之一。

四、随机动态模型及其求解

（一）系统性风险测度变量选择

不同类型的支付系统的系统性风险各有其来源。在RTGS 系统中，虽然没有信用风险，但是由于每一个理性的参与银行出于利益最大化的考虑，会尽量减持流动性资产和延迟履行支付义务，可能会出现僵锁(Gird Lock)现象。

僵锁的严重程度和规模通常由未结算金额比例(Unsettled Payment Indicator，以下简称UPI)来衡量。UPI 的定义如下：

根据之前的研究，UPI 是作为衡量RTGS 支付系统中系统性风险最为常用的变量(蒋凌子，2016)。UPI 越高，意味着系统性风险越大。特别需要指出的是，虽然UPI 是一个来自支付系统的指标，但是与采用其他方法研究系统性风险的文献相比较，它和DD 危机距离(Distance to Distress)这个指标非常类似，都在一定程度上刻画了需要履行付款义务的缺口大小，注意两者的关系可以拉近不同研究工作的距离。

（二）随机NWMY 方程和系统性风险演化模型

NWMY 方程是描述一个具有传染性的事件(Event)(比如交通堵塞、火灾、支付指令未能及时结算及其连锁效应等)在发生以后，它的总量/规模(Volume)在其所处的小世界网络(Small World)中如何传染、演化的方程。在NWMY 方程被提出之前，对于复杂网络中某一具有传染性的事件的总量测度主要都是通过计算机仿真来完成的，各影响因素之间、影响因素和被解释变量之间的关系不够明确、直观，缺乏解析研究理论。1999 年，Newman 和Watts 首次提出了这一方程的最初形式并进行了求解，解决了以上问题，奠定了这一领域研究的基石(Newman 和Watts，1999)。随后，Moukarzel 对Newman-Watts 模型进行了更为详细的阐述(Moukarzel，1999)。2001 年，Yang 对模型进行了拓展，加入了一个非线性项来刻画系统中的“摩擦”效应(Yang，2001)。经过以上发展过程，NWMY 理论得以建立，为复杂网络中传染问题的研究开创了新局面。

通常，NWMY 方程如下：

其中，ξ是刻画小世界网络中节点之间关联程度的变量，根据Newman 和Watts 的解释，它实际就是网络的平均路径长度；δ是时滞；μ是模型中的非线性因子，刻画非线性效应的强弱。非线性效应是对传染性事件在网络中扩散的一种抑制作用，在文献(Yang，2001)中限定 1μ≪ 。金融网络中的非线性效应是真实存在的，对此的详细解释可见后文。

方程(3)中有时滞δ，求解时较难处理，但可以通过变量的平移变换消去，同时对变量进行线性变换，可得：

第三部分的实证工作表明中国的银行间复杂网络具有小世界性。根据NWMY 理论，在具有小世界性的银行网络中，UPI 的总量的发展演化应该满足NWMY 方程。但NWMY 方程是一个理想化的模型，没有考虑外界随机因素的作用。在现实世界，大多数事件的发展变化都会受到随机因素的干扰，UPI 也一样，它的产生和累积过程会受到很多随机因素影响。因此，UPI 的总量是一个随机变量(过程)，需要对它进行进一步改造，把随机因素的影响考虑进去。参照随机数学、统计物理学中常用的做法(胡岗，1994)，可以把NWMY 方程(4)拓展为一个随机微分方程，以更贴近现实。具体来说就是在方程中增加一项随机力(Stochastic Force) ( )ζt ，得到随机NWMY 方程：

上式中D 为噪声强度，·〈〉为期望值。

从方程(5)的形式来看，它的右端由三项组成，各项的经济学意义如下。

(1) 第一项表示银行系统在受到冲击以后内部的风险随时间演化而增加，这是因为银行间业务的高度关联性，彼此联结成复杂网络后连锁效应的体现。

(2) 第二项正如前文所讲的，是以非线性形式出现的，主要代表银行网络系统本身对风险的抑制和吸收作用的能力，它主要来自两个方面：一是系统内部实施的各项预防风险的政策、策略，无论监管部门还是系统中的银行自身，都会对风险有着预防措施。比如，对比巴塞尔协议II，巴塞尔协议III 在银行资本构成、资产质量、资本充足率以及一些流动性指标方面都大幅度提升了监管要求，这显然会对风险产生较强的抑制作用。二是银行间RTGS 型支付结算系统中会有一些旨在减少风险的流动性管理机制。比如，我国第二代现代化支付系统新增了“大额清算排队业务撮合”功能，及时处理因参与银行账户头寸不足导致的无法实时结算，减小了因流动性风险引发的系统性风险，这一策略就会对出现的风险产生抑制作用。

(3) 第三项是噪声扰动项，噪声强度代表支付系统外部经济环境、政策环境等的稳定程度，噪声强度越大表明外部环境对银行网络的随机干扰作用越大。

（三）系统性风险概率分布函数演化模型

如果把系统性风险视为一个随机过程，那么还应该分析它的概率分布函数。现有的文献对此鲜有涉及。这个概率分布函数的演化遵从什么规律？要解决这个问题，仍需要以随机NWMY 方程为出发点。利用Kramers-Moyal 展开方法(胡岗，1994)，可以推导出这个随机过程的概率分布函数演化所满足的方程，统计物理学中称之为Fokker-Planck 方程。该方程如下：

（四）模型求解

前文建立的关于风险的概率分布的Fokker-Planck 方程(7)是一个二阶偏微分方程，按照之前文献(胡岗，1994)所述，采用传统方法很难求得这个方程的精确解析解。但是，如果选择适当的求解方法，则可得到它的解析形式的近似解。由于代数动力学解法能够较好地实现方程代数结构的保真(即尽可能少地被破坏)，与同类方法相比具有较为明显的优势(王顺金等，2005)，以下将采用这种方法来解析求解方程。

限于篇幅，直接给出计算结果，方程(7)的解为(保留到二阶)：

二阶系数具体表示为：

考虑到数值模拟和解析表达式的图像不可能完全一致，从以上计算结果来看，采用代数动力学解法得到的概率分布的解析结果是可靠的，可以此为基础进行下一步的分析。

图2 t＝0时刻解析解

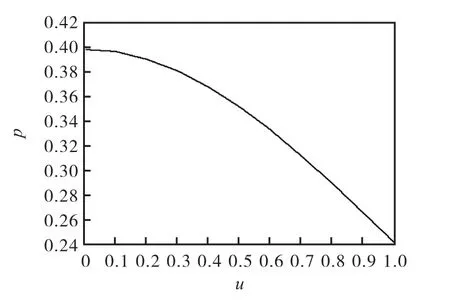
图3 t＝0时刻数值解

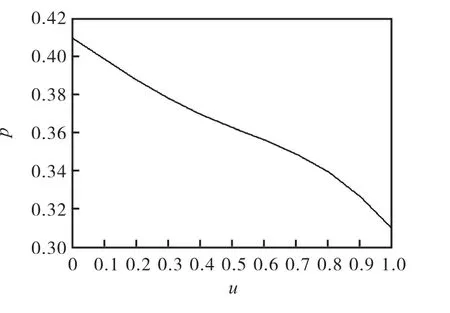
图4 t＝0.15时刻解析解

图5 t＝0.15时刻数值解

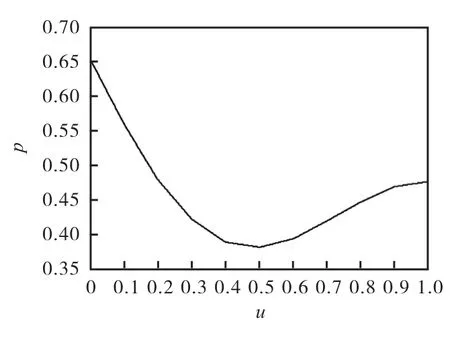
图6 t＝0.35时刻解析解

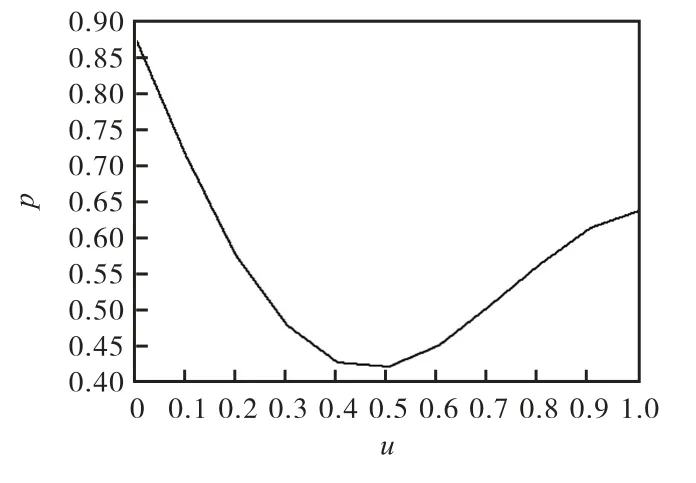
图7 t＝0.35时刻数值解

图8 t＝1.5时刻解析解

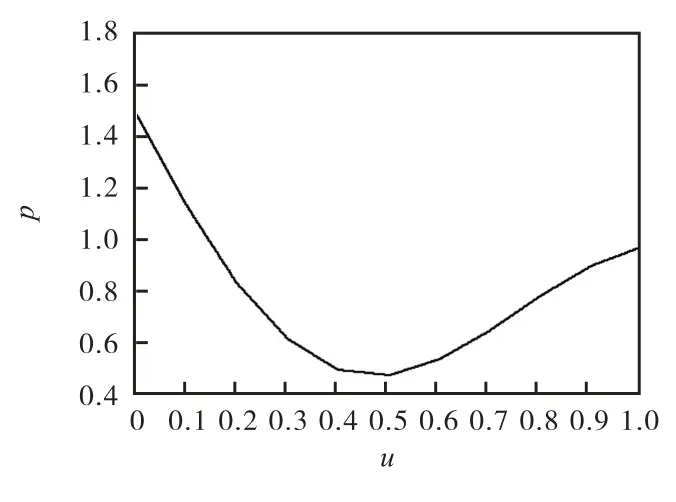
图9 t＝1.5时刻数值解

另外，从上图2、图4、图6、图8 可以看出，随着时间的推移，首先UPI 的概率分布是要发生变化的。初始时刻是标准正态分布的右半侧的一部分，随着时间的前进，这个概率分布曲线的尾部与坐标横轴的距离越来越大，出现了典型的胖尾(Fat Tail)特征。这说明，如果UPI 达到一定的程度以后，如果没有外部的干预(比如流动性注入、监管介入)，尾部风险变大，出现极端风险事件的可能性就增大了。

五、系统性风险期望值及分布函数影响因素分析

根据方程(7)，银行网络的特性体现在三个参数上：ξ、μ和D。ξ和μ反映了网络的固有属性，是内生的参数；D 反映了外部环境对网络的影响，是外生的。ξ已在第三部分的实证确定。以下主要考察另外两个参数的变化对系统性风险的影响。

（一）非线性效应与风险期望值

银行网络的非线性效应主要由随机NWMY 方程的参数μ体现。在其他参数不变的情况下，增大非线性参数，即取 0.1μ= ，计算结果如图11 所示。

图11 与图10 对比可以看出，在参数μ增大以后，图11 中风险的期望值曲线的峰值要小于图10 中风险峰值，这体现出非线性效应对风险的抑制、抵御作用。另外，非线性参数μ对于UPI 峰值出现的时间是有影响的，图11 的峰值对应的时间取值更大，约在 0.5t= 左右。这说明，较大的非线性项的系数μ可以推迟未结算金额比例峰值出现的时间，当然这是因为支付系统对风险的抵御、吸收能力更强。未结算金额比例峰值出现时间的推后，在现实中是有显著意义的，因为未结算金额比例峰值意味着风险最大，此时极有可能发生系统性风险事件，而峰值出现时间的推后可以为监管部门的防范、救助工作赢得时间。

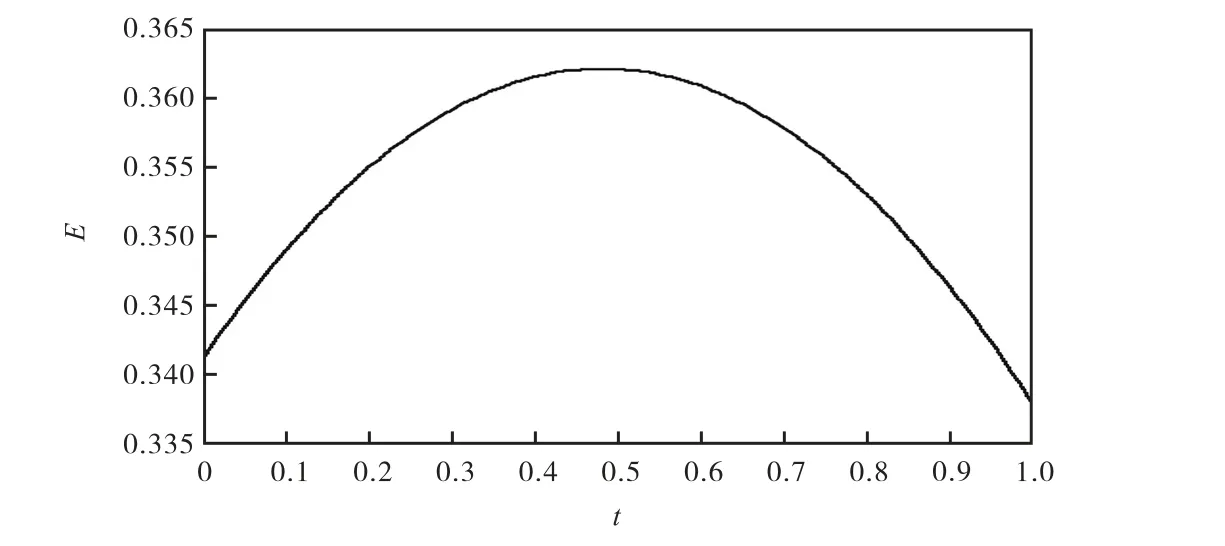
图10 μ＝0.01 时的UPI期望

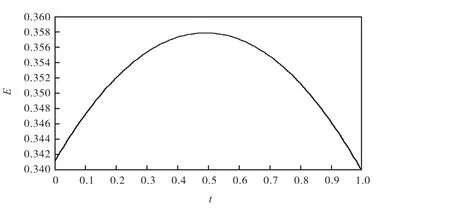
图11 μ＝0.1 时的UPI期望

（二）非线性、噪声与风险概率分布函数

接下来探讨非线性效应和噪声，即模型中的μ和D 两个参数分别对系统性风险的概率分布函数的影响。

1. 非线性因子μ的变化对概率分布的影响

前已述及，非线性参数μ代表着银行网络自身对风险扩散的制约作用，制约的程度因不同支付系统的结构、机制设计等而不同。令ξ= 1.5，D = 0.1不变，由于文献(Yang，2001)中要求μ≪ 1，因此分别取μ= 0.001、μ= 0.01、μ= 0.1，代表非线性作用由弱到强，得到结果如图12、图13 和图14。

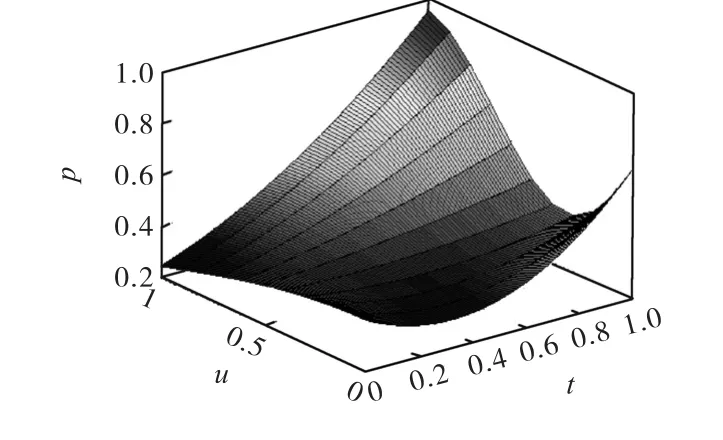
图12 μ＝0.001 时未结算金额比例的分布

图13 μ＝0.01 时未结算金额比例的分布

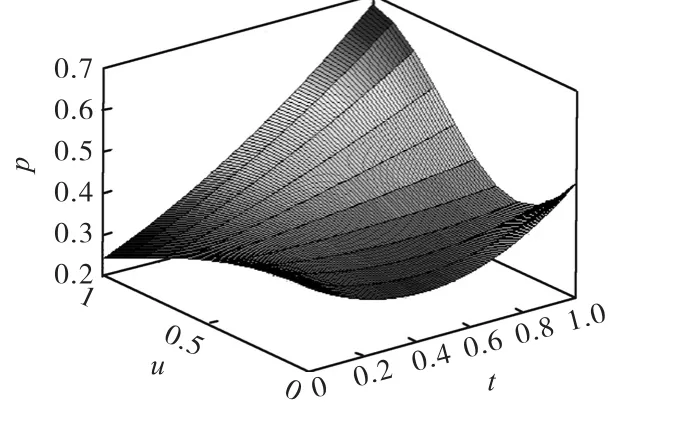
图14 μ＝0.1 时未结算金额比例的分布

从图13 可知，首先UPI 的概率分布的形状是会随时间发生变化的，分布曲线开始是头部(UPI 较小的区域)对应的概率大而尾部(UPI 较大的区域)对应的概率小，经过一段时间后会变成头部和尾部UPI 对应的概率都增大了(当然尾部UPI 对应的概率增幅更大)，而介于头部和尾部之间的UPI 对应的概率减小了。这说明在不改变参数的情况下，风险的概率分布会随时间发生变化。另外，分布函数的尾部变厚，可以称之为出现了厚尾(Fat Tail)现象，表明出现极端风险事件的概率增大了。

接下来，在μ的三组不同的取值下，对比图12、图13 和图14 三幅图，演化同样的时间后，三幅图中分布函数曲线的头部和尾部对应的概率都增大了，但是增幅是不一样的。非线性参数μ越大，相应的增幅越小，较大的μ就可以起到减小厚尾的“厚度”的作用，对于增强对极端风险事件的预防能力、抑制尾部风险很有益处。这就印证了前文述及的一个事实，那就是银行网络的非线性效应对风险会有抑制作用，非线性强度越高，抑制、吸收作用就越大。

前文已述，在现实的银行网络中，非线性效应是由多方面因素的合力形成的。比如，如果银行的流动性管理水平普遍较高，或者对行业的监管政策得当，即使出现了一定规模的支付指令结算不了的情况，也可能因为较好的管理策略，系统性风险逐渐被网络自身吸收。再如，在结算机制的设计方面，如果采用了合理的、先进的流动性节约管理方法(拆分算法、绕行算法等)，也可以加强支付系统对于风险的自我防御、自我吸收能力。因此，有不少增强银行网络非线性效应的措施，凸显了央行在支付系统建设顶层设计方面的重大责任和重要作用。

2. 噪声强度的变化对概率分布的影响

前已述及，噪声强度表示支付系统外部经济环境、政策环境等的稳定程度，噪声强度越大代表外部环境越不稳定，在模型中主要由参数D 体现出来。如前，在 1.5ξ= ，μ= 0.01的情况下，分别取 D= 0.01，D = 0.1，D = 0.5，得到结果如图15、图16和图17。

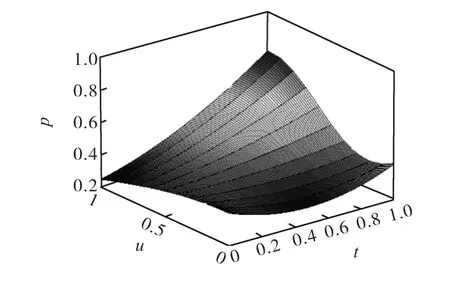
图15 D＝0.01 时未结算金额比例的分布

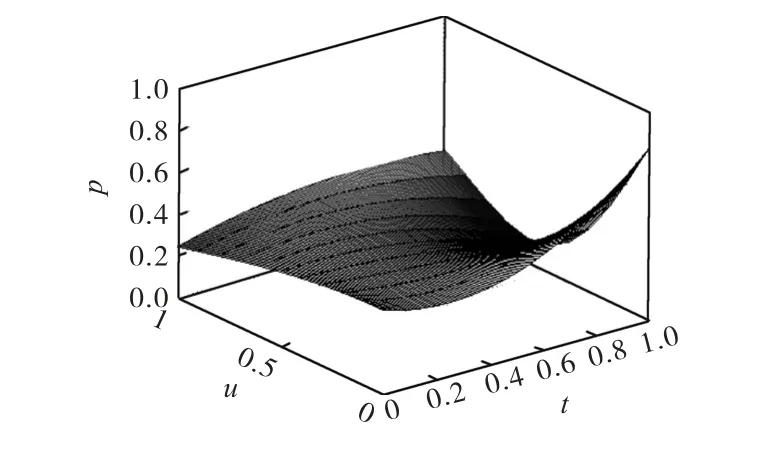
图17 D＝0.5 时未结算金额比例的分布

图16 D＝0.1 时未结算金额比例的分布

从上图结果可知，当噪声处于较低水平时，如D＝0.1，噪声强度的变化对风险水平的影响不太大；但是当噪声强度超过一定水平，如D＝0.5，可以明显地改变UPI 概率分布的形状。具体来讲，初始时刻UPI 的概率分布呈现出小的UPI 对应的概率大而大的UPI 对应的概率小这样一种较为理想的图景。噪声的加入，尤其是强度逐渐增大时，原先同样取值的UPI 对应的概率有明显改变：同样小的UPI 对应的概率增大了，而同样大的UPI 对应的概率减小了。也就是说，噪声尤其是强度比较大的噪声，使得UPI 对应的概率值更加平均，具有平均效应。

以上理论实验对应的现实情况可以理解为，银行网络中一旦出现一定规模的支付指令未结算情况，在外界的随机事件的影响不太大的时候，网络自身能够抵御、吸收这些干扰，因此对网络中系统性风险的发展、变化的影响不大。但是，当受到对系统影响较大的随机事件(比如规模较大的金融危机)的干扰时，会使得网络中系统性风险的变化、发展情况复杂化，因为多种结果出现的概率都差不多，事实上风险是增大了，这对于监管措施、救助策略的实施是不小的挑战。

六、政策建议

现代经济中，由于金融机构相互紧密关联，系统性风险在参与支付系统的银行之间传染，会对一国的金融安全产生严重威胁。这就需要建立起金融业的宏观审慎监管制度，从全局去评估和管理风险。要做好宏观审慎监管，准确地掌握银行体系中的系统性风险及其概率分布函数的演化规律，特别是能够比较全面展现各个相关因素准确 函数关系、数理模型形式的规律，就成为最核心的工作之一，也是其他相关工作的基础之一。

在以上研究工作的基础上，有如下政策启示。

首先，加强对支付系统内流动性风险和系统重要性银行的动态监测、管理。前文的研究说明系统性风险及其概率分布具有时变性和动态性，这就决定了需要对风险进行密切监测。对其中银行的系统重要性则需要开展动态评估。在RTGS 支付系统中，系统性风险主要来自流动性风险。因此，对系统内商业银行的流动性进行实时监测，就等于能够及时掌握风险的变化状况。当然，也许系统中反映的银行的流动性信息不够全面，但仍然能显现出主要的情况。在掌握了商业银行流动性情况的基础上，就可以开展对其履行支付结算指令行为的管理。比如，实施高额罚息贷款就是央行向头寸不足的商业银行提供的强制性的、惩罚性的高息贷款，防止商业银行出现大的流动性风险。对于系统重要性银行的评估，2018 年11 月27 日“一行两会”正式发布《关于完善系统重要性金融机构监管的指导意见》，为这项工作提供了良好的政策保障和开端，但还需要大量进一步的工作来落实。

其次，进一步优化支付系统工作机制。前文在讨论银行间网络的非线性效应对风险的吸收、抑制作用时就讨论过，一个好的支付系统本身就有着一定抵御风险的能力，这就需要不断地优化系统。与发达国家相比，中国支付系统建设起步较晚，历史较短，需要借鉴经验并不断完善。

尽管目前国际上主要国家都采用了RTGS 支付系统——原则上是实时结算，但是参与支付系统的银行通常会因追求自身利益最大化而选择延迟一定时间，等待外部转入的流动性完成支付，相应的未能及时结算的指令就会进入队列等待，这其中就存在流动性风险。如果加入拆分(Splitting)算法，本来在队列中等待的部分指令就可以尽快完成结算，降低风险。

最后，进一步优化日间信贷制度。合理的日间信贷既是救助体系的一部分，也是支付系统建设的组成部分，因为这些信贷活动具体也需要在支付系统中实现。自动质押融资和日间透支，都是央行对支付系统的参与银行的流动性的一种调节手段，同时也可以通过对日间信贷的合理定价来管理系统中参与银行的延迟支付行为，减少延迟结算的数量，降低风险。