页岩油藏表观液体渗透率的分形表征方法
杨元亮
(中国石化新疆新春石油开发有限责任公司,山东东营 257000)
目前,页岩油藏已成为油气开发的一个热点领域,页岩油藏的勘探、开发及油气渗流理论迅速发展[1-4]。渗透率反映流体在多孔介质中的渗流规律和基本特征,被广泛应用于油藏开发动态分析、油藏数值模拟技术和产量评估,是油田开发中一个非常重要的参数和研究热点。页岩油藏具有源储一体、微纳米级孔隙发育和储集物性差的特征,属于超低渗透致密储层。针对低渗透油藏和致密油藏的渗流机理及实验研究相对较多,建立了基于边界层理论的非线性渗流理论,从理论和实验方面分析了边界层效应对渗流规律的影响[5-6]。但是有关页岩油藏的有效渗流能力的影响因素及表征方法的研究仍处于初级阶段[7-10]。
负滑移长度定义为在纳米孔壁处不流动流体的厚度[11]。研究结果表明[12-15]:页岩油藏孔隙细小,半径为1~200 nm 的微纳米孔隙发育,多数孔隙半径小于5 nm[16],液-固界面间的分子作用力较强。流体在页岩孔隙壁面存在速度滑移现象,负滑移长度与孔隙润湿性和孔隙类型相关[17-19]。由于纳米尺度和滑移流动的复杂性,有必要建立考虑页岩油藏滑移效应的渗透率表征方法。当从宏观尺度到纳米尺度时,液体流动动力学发生变化:相对于传统的连续介质流体流动方程,在纳米尺度范围内负滑移长度随系统特征尺度的减小和摩擦力的减小而增大,使得连续无滑移流动假设不再成立,达西渗流规律不适用于页岩油藏中液体流量的测定[20-22]。WANG 等应用分子动力学方法研究流体在无机和有机纳米孔的运移机制,建立了考虑负滑移长度和表观黏度的液烃运移机制[23];苏玉亮等结合页岩孔隙润湿特性,考虑流体吸附、速度滑移及流体物性变化作用机制,引入页岩孔隙迂曲度、孔隙度和有机孔含量等结构参数,在单毛细管模型的基础上建立页岩油藏微纳米多孔介质表观液体渗透率模型,研究了不同运移机制对页岩油藏表观液体渗透率的影响[24]。然而这些模型不能描述孔隙结构特征[25]对表观液体渗透率的影响。研究页岩油藏的有效渗流能力,建立页岩油藏表观液体渗透率的表征方法是评价页岩油藏有效渗流能力的一种重要方法,对形成页岩油藏数值模拟技术、建立产量预测模型和研究页岩油藏开发产量变化特征具有重要的现实意义。
1982年美国数学家MANDELBROT 创建了分形几何理论[26],该理论被广泛用于描述具有自相似性的复杂几何空间,天然多孔介质的微孔隙结构已被证明具有分形特征[27-28]。许多学者应用分形理论研究页岩油藏的孔隙结构特征[29]、页岩气藏的表观液体渗透率[30]和建立油水相对渗透率理论模型[31-33]。页岩油藏岩相类型复杂,孔隙类型多样,孔隙尺寸相差较大,润湿性各不相同,滑移特征不同,有效预测页岩油藏的渗透率仍然具有挑战性。为此,笔者基于多孔介质分形理论,对Hagen-Poiseuille 流动方程[34]进行滑移修正,定量描述微纳米管内考虑滑移现象的流动特征,并在此基础上建立考虑负滑移特征的页岩油藏表观液体渗透率模型,定量分析迂曲度、孔隙介质的分形维数和负滑移长度等因素对表观液体渗透率的影响。
1 考虑负滑移长度的表观液体渗透率模型
1.1 考虑负滑移长度的微纳米管流量模型
流体在微纳米管中的流动表现为牛顿流体的流动特征。牛顿流体的应力本构方程为[34]:

对半径为R的微纳米管内流动半径r处流体的应变,应用(1)式可描述为:
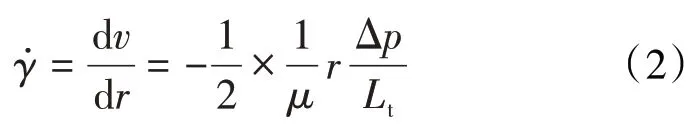
假设流体的负滑移长度为δ,相当于有效渗流半径减小δ,对(2)式从r到R-δ进行积分,得:
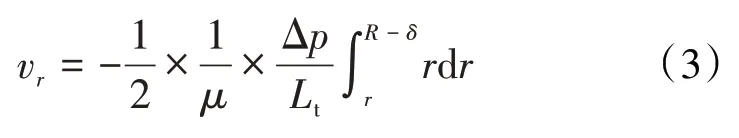
则得到流体沿微纳米管半径方向的速度分布为:
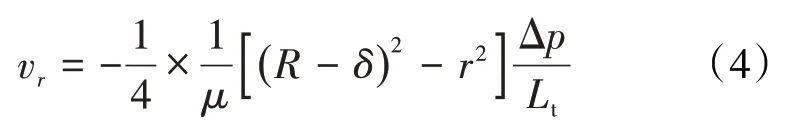
对(4)式沿微纳米管半径方向进行积分,得到流体通过单个微纳米管的流量为:
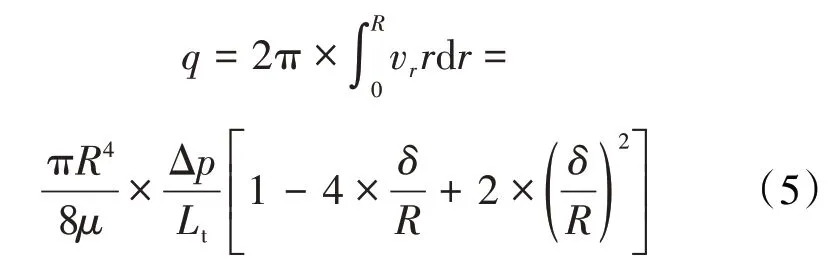
根据(5)式,得到液体在微纳米管中流动的平均速度为:
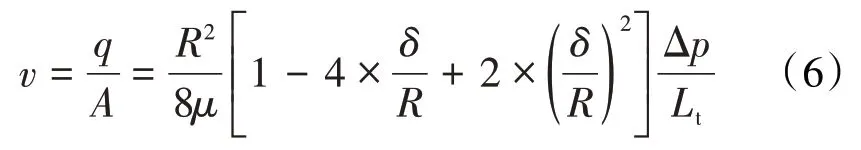
(5)式为考虑负滑移长度的微纳米管流量模型,(6)式为考虑负滑移长度的微纳米管流速模型。当负滑移长度为0时,(5)式即为描述流体在微纳米管中流动的Hagen-Poiseuille 方程。因此,(5)式被定义为考虑负滑移长度的修正Hagen-Poiseuille 方程,可用来量化研究微纳米管中负滑移长度对渗流速度的影响。
1.2 表观液体渗透率模型
令多孔介质的迂曲度为弯曲微纳米管的真实长度与视长度之比,即:

将(7)式代入(5)式,得到考虑迂曲度的单个微纳米管流量模型为:
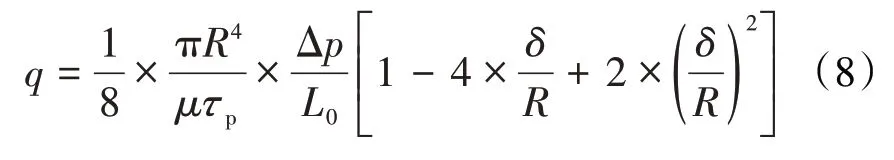
根据多孔介质的分形理论,将分形多孔介质的总流量视为通过半径为(rmin,rmax)微纳米管的流量之和,即:
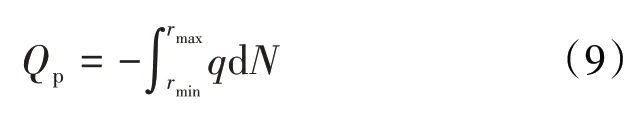
其中,dN为平均孔隙半径在r和r+dr范围内的总孔隙数[35],即:
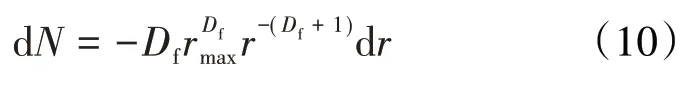
将(8)式和(10)式代入(9)式,得通过渗流横截面积A的总流量为:
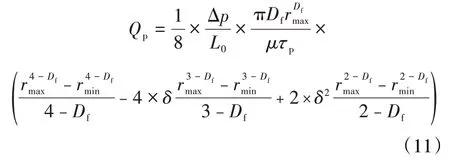
因此,根据多孔介质的分形理论,考虑负滑移长度的流量方程为:

根据达西渗流方程,通过渗流横截面积为A,长度为L0的真实岩心的流量为:
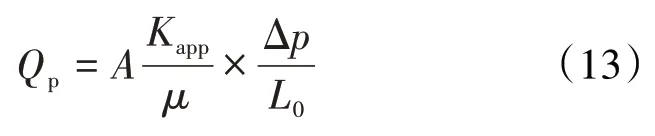
假设该真实岩心的迂曲度与微纳米管模型的迂曲度相等,当真实岩心和分形多孔介质的渗流阻力相等时,则(12)式和(13)式描述的流量相等,即:
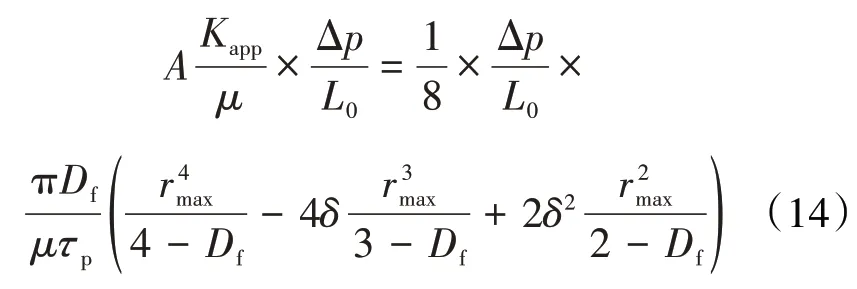
由(14)式得到表观液体渗透率模型为:
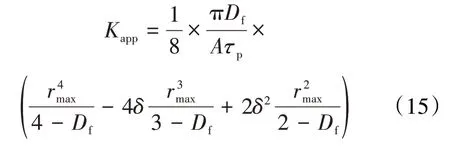
根据多孔介质的分形理论,岩心的渗流横截面积可表示为[36]:
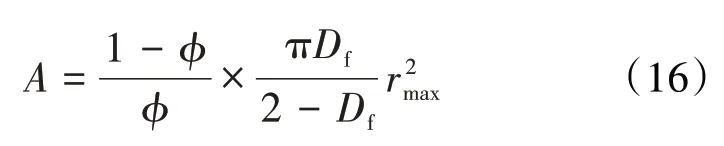
将(16)式代入(15)式中,得到考虑负滑移长度的页岩油藏的表观液体渗透率为:
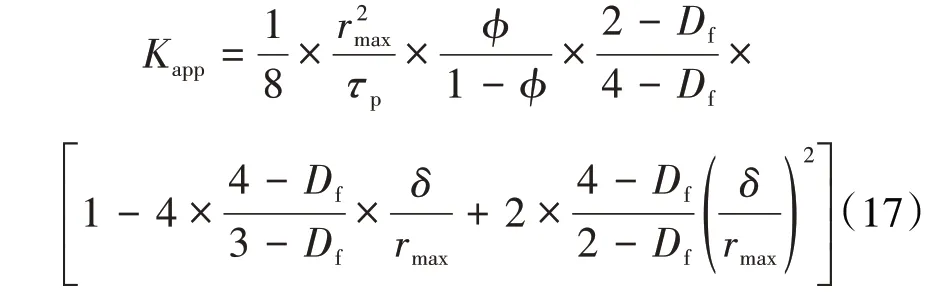
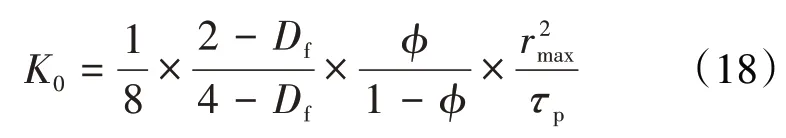
其中,多孔介质迂曲度的计算式为[37]:
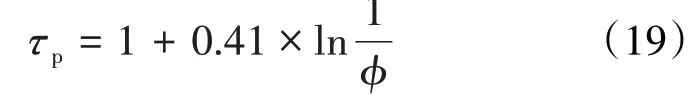
根据(17)和(18)式,得表观液体渗透率与达西渗透率之比为:
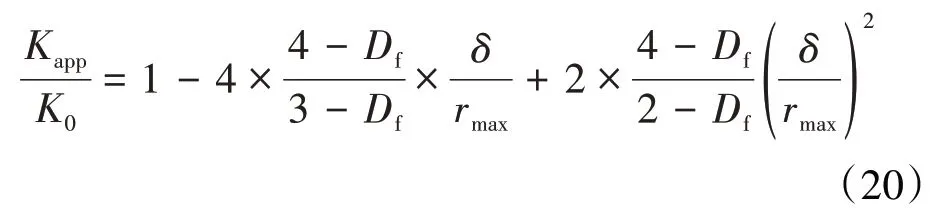
(17)式即为基于多孔介质分形理论建立的页岩油藏表观液体渗透率模型。从该式中可以看出,页岩油藏表观液体渗透率受页岩油藏的孔隙分形维数、孔隙度、迂曲度和最大孔隙半径的影响,更重要的是(17)式体现了负滑移长度对页岩油藏表观液体渗透率的影响。
2 参数敏感性分析
为研究各种参数对页岩中液体流动的影响进行敏感性分析,各参数值见表1。

表1 岩心及流体的基本参数Table1 Basic parameters of core and liquid
2.1 微纳米管半径对平均流体渗流速度的影响
在微纳米管半径为20~400 nm,负滑移长度为10 nm 的条件下,应用(6)式计算单位长度微纳米管内平均流体流动速度。结果(图1)表明,在微纳米管两端驱动压差和流体性质相同的条件下,当微纳米管半径与负滑移长度接近时,微纳米管内流体的平均渗流速度几乎为0;在相同负滑移长度的条件下,不同半径微纳米管内平均流体渗流速度差异较大,平均流体渗流速度随着微纳米管半径的增加而增加。

图1 不同微纳米管半径下平均流体渗流速度Fig.1 Average percolation velocity at different radii of micro/nanotubes
2.2 负滑移长度对平均流体渗流速度的影响
页岩油藏孔隙半径小,负滑移长度对流体渗流速度和表观液体渗透率的影响不可忽略,由于负滑移长度的存在,流体的有效渗流半径减小。应用(6)式计算不同负滑移长度(10,20 和30 nm)对平均流体渗流速度的影响,由结果(图2)可知,负滑移长度越大,微纳米管内流体的平均渗流速度越小。
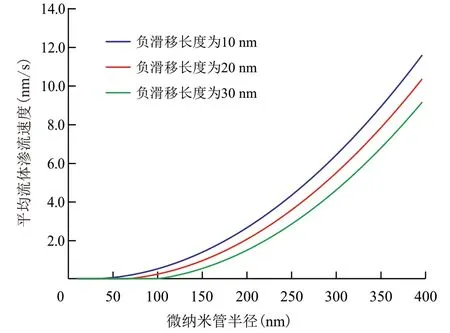
图2 负滑移长度对平均流体渗流速度的影响Fig.2 Influence of negative slip length on average percolation velocity
2.3 驱替压差对平均流体渗流速度的影响
由驱替压差对平均流体渗流速度的影响(图3)可见,在负滑移长度为10 nm 的条件下,平均流体渗流速度随驱替压差的增大而增大;当微纳米管半径较小时,负滑移长度相对于微纳米管半径不可忽略,驱替压差对平均流体渗流速度影响较小。

图3 驱替压差对平均流体渗流速度的影响Fig.3 Influence of displacement pressure difference on average percolation velocity
2.4 负滑移长度对流体渗流速度分布的影响
所选用的微纳米管半径分别为40,100 和400 nm,负滑移长度分别为10,20,30 nm。微纳米管内流体渗流速度的分布(图4)表明:在同一个微纳米管内,沿微纳米管半径方向流体的渗流速度呈现对称分布,在靠近微纳米管壁的位置处流体渗流速度为0,在微纳米管中心流体渗流速度最大;且负滑移长度越大,流体的有效渗流半径越小,流体渗流速度分布越窄;负滑移长度越大,微纳米管中心的流体渗流速度越小。对比不同半径微纳米管内平均流体渗流速度,微纳米管半径越大负滑移长度对平均流体渗流速度分布的影响越小,且微纳米管中心位置处的平均流体渗流速度随微纳米管半径的增大而增大。
2.5 多孔介质最大孔隙半径对表观液体渗透率的影响
在不同的多孔介质最大孔隙半径下,负滑移长度对表观液体渗透率与达西渗透率之比的影响(图5)表明:在某一最大孔隙半径下,表观液体渗透率与达西渗透率之比随负滑移长度的增加而减小;在相同负滑移长度条件下,最大孔隙半径越大,负滑移长度对表观液体渗透率与达西渗透率之比的影响越小,即随着平均孔隙半径的增大,表观液体渗透率和达西渗透率之间的差异逐渐缩小。根据(20)式可知,当负滑移长度与多孔介质最大孔隙半径之比可以忽略不计时,负滑移长度对表观液体渗透率与达西渗透率之比的影响也可以忽略。反之,当负滑移长度与多孔介质的最大孔隙半径之比不可以忽略时,负滑移长度在一定程度上将影响表观液体渗透率与达西渗透率之比。
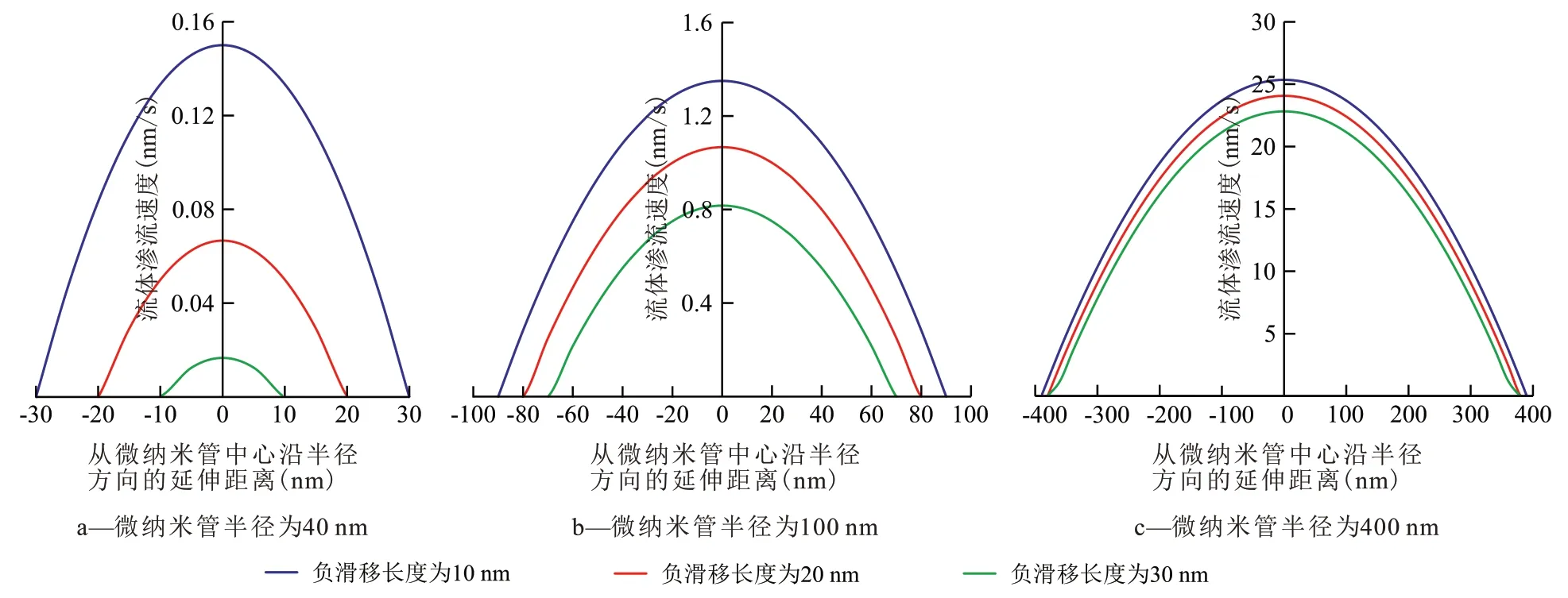
图4 微纳米管内流体渗流速度的分布Fig.4 Distribution of average percolation velocity in micro/nanotubes
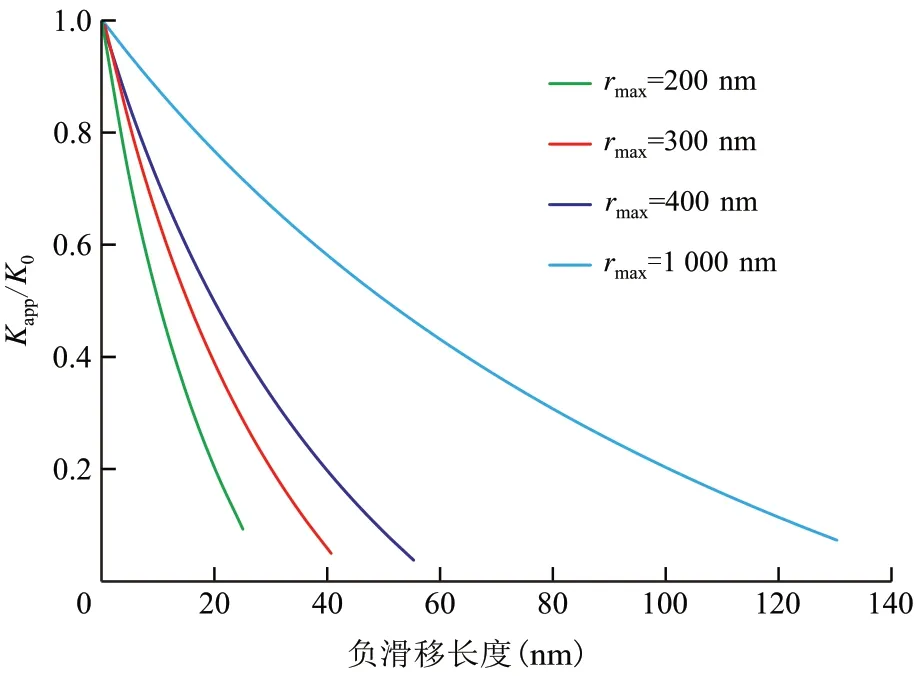
图5 不同多孔介质最大孔隙半径下负滑移长度对表观液体渗透率与达西渗透率之比的影响Fig.5 Influence of negative slip length on ratio of apparent liquid permeability to Darcy permeability at different maximum pore radii of porous media
当迂曲度为1.5,孔隙度为0.05,分形维数为1.5时,对比研究了最大孔隙半径分别为200,300 和400 nm 时负滑移长度对表观液体渗透率的影响。由结果(图6)可见,在不同的最大孔隙半径条件下负滑移长度对表观液体渗透率的影响体现出相同的趋势,随着负滑移长度的增加,表观液体渗透率减小。对比不同孔隙半径的负滑移长度对表观液体渗透率的影响可知,相同负滑移长度时,平均孔隙半径越大,负滑移长度对表观液体渗透率的影响越小。
2.6 迂曲度对表观液体渗透率的影响
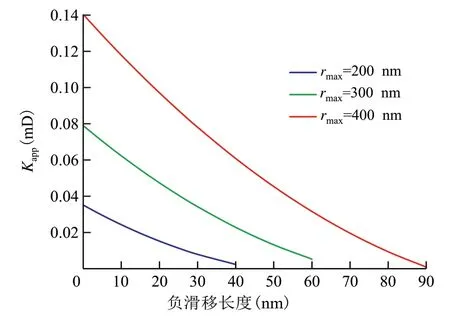
图6 不同多孔介质最大孔隙半径下负滑移长度对表观液体渗透率的影响Fig.6 Influence of negative slip length on apparent liquid permeability at different maximum pore radii of porous media
迂曲度是影响多孔介质渗透率的重要参数,表征多孔介质中不同尺寸孔隙的弯曲程度。当最大孔隙半径为300 nm,负滑移长度为10 nm,孔隙度为0.05,分形维数为1.5 时,由迂曲度对表观液体渗透率的影响(图7)可见,随着迂曲度的增加表观液体渗透率降低。孔隙空间流动的弯曲程度增加,孔隙结构越复杂,导致液体流动阻力增加,表观液体渗透率降低。

图7 迂曲度对表观液体渗透率的影响Fig.7 Influence of tortuosity on apparent liquid permeability
2.7 孔隙分形维数对表观液体渗透率的影响
孔隙分形维数是反映多孔介质中不同尺寸孔隙的分布和非均质性对渗透率影响的重要参数,孔隙分形维数越大,孔隙尺寸分布越均匀,非均质性越弱。当最大孔隙半径为300 nm,负滑移长度为10 nm,迂曲度为1.5时,由孔隙分形维数对页岩油藏表观液体渗透率的影响(图8)可知,表观液体渗透率随孔隙分形维数的增加而增大。对于给定的多孔介质,当孔隙介质的最大孔隙半径与最小孔隙半径给定时,根据多孔介质的分形理论[17],随着孔隙分形维数的增大,单位面积内的孔隙数量增多,液体渗流通道增多,渗流阻力减小,表观液体渗透率增大。
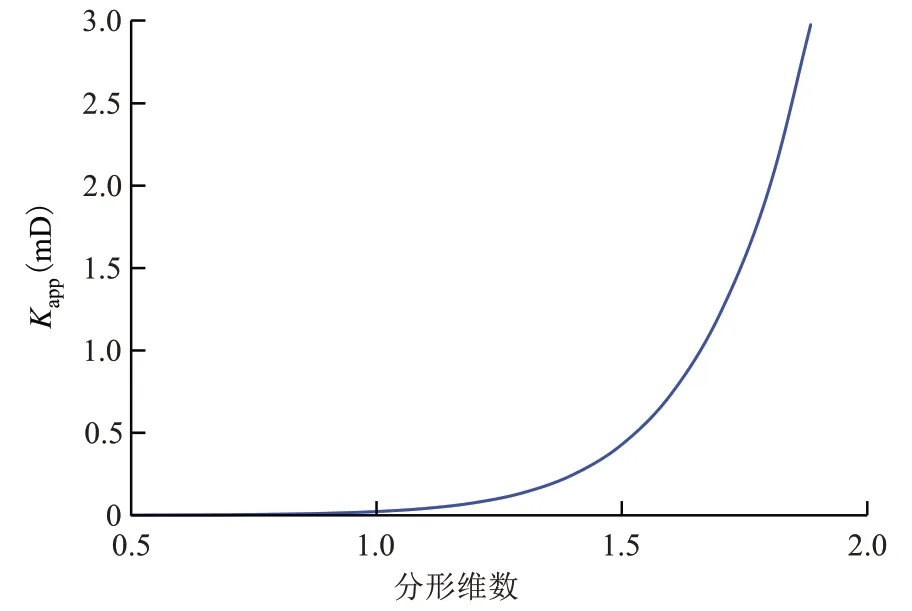
图8 孔隙分形维数对表观液体渗透率的影响Fig.8 Influence of fractal dimensions on apparent liquid permeability
3 模型应用
为预测页岩油藏的表观液体渗透率,选用胜利油区某页岩油藏的岩心开展高压压汞实验,并用所建表观液体渗透率模型(17)式与实验测试结果进行对比。岩心样品取自该区块的沙三段,深度为3 296~3 314 m,纹层状泥质灰岩相。实验测试孔隙度为3.22%,空气渗透率为0.325 mD。在实验设备及条件下,测得最小孔隙半径为0.003 μm,最大孔隙半径为0.75 μm。由(19)式计算得到岩心迂曲度为2.4,应用(18)式计算该页岩储层的达西渗透率为0.231 mD,仅为气测渗透率的71.2%。该区块地层原油黏度为1.5 mPa·s,根据文献[38]提供的方法计算得地层条件下原油的负滑移长度为10 nm,应用(17)式计算得考虑负滑移长度的页岩储层表观液体渗透率为0.211 mD,由滑移效应引起的渗透率损失为8.6%。
4 结论
针对页岩油藏微纳米孔隙中的滑移现象,建立考虑负滑移长度的修正Hagen-Poiseuille 方程和平均速度方程。在多孔介质分形理论的基础上,建立考虑负滑移长度的页岩油藏的表观液体渗透率模型。页岩油藏表观液体渗透率不仅受孔隙结构、孔隙度、迂曲度和孔隙半径的影响,也与液体负滑移长度相关。
页岩油藏孔隙半径小,负滑移长度对表观液体渗透率的影响不可忽略。负滑移长度越大,流体在微纳米管中的平均渗流速度越小;表观液体渗透率与达西渗透率之比随负滑移长度的增加而减小;孔隙半径越小,负滑移长度对表观液体渗透率的影响越大。因此,寻找负滑移长度的描述方法和建立负滑移长度的测量方法对确定页岩油藏表观液体渗透率和评价页岩油藏的可动性至关重要。
符号解释
A——分形多孔介质岩心的渗流横截面积,μm2;
Df——孔隙分形维数,在二维平面上0 <Df<2,三维空间上0 <Df<3;
Kapp——表观液体渗透率,D;
K0——达西渗透率,D;
L0——多孔介质的视长度,μm;
Lt——弯曲微纳米管的真实长度,μm;
N——微纳米孔隙半径分布在(rmin,rmax)范围内的微纳米总数;
Δp——驱替压力,Pa;
q——流体通过单个微纳米管的流量,μm3/s;
Qp——分形多孔介质的总流量,μm3/s;
r——微纳米管内流体流动半径,μm;
rmin——多孔介质的最小孔隙半径,μm;
rmax——多孔介质的最大孔隙半径,μm;
R——微纳米管半径,μm;
v——液体在微纳米管中流动的平均速度,μm/s;
vr——微纳米管内流动半径r处流体流动速度,μm/s;
˙——流体的应变,s-1;
δ——负滑移长度,μm;
μ——流体黏度,Pa·s;
τ——流体所受的切应力,Pa;
τp——多孔介质的迂曲度;
φ——多孔介质的孔隙度。

