水相分流量全过程有理式模型的建立及应用

吕 晶，刘显太，孙业恒，陈德坡，黄迎松

（1.中国石化胜利石油管理局有限公司博士后科研工作站，山东东营 257001；2.中国石化胜利油田分公司，山东东营 257001；3.中国石化胜利油田分公司勘探开发研究院，山东东营 257015）

水相分流量曲线是研究油藏开发动态的重要基础资料之一，利用水相分流量曲线能够分析油藏含水率上升规律、水驱油藏含水饱和度分布、地层平均含水饱和度及采出程度、驱油效率等重要开发指标，对分析油藏开发动态意义重大［1-3］。目前水相分流量曲线的获取方法是利用室内相对渗透率测试数据，通过水相分流量定义式计算得到［4-5］。由于室内实验驱替倍数有限，不能直接获得残余油饱和度，水相分流量方程的末端值是估算所得。理论上水相分流量的数值为0～1，但现阶段针对水相分流量方程的近似拟合模型，如经典逻辑斯蒂方程，其方程形式决定了水相分流量计算结果在初始时刻无法等于0，同时曲线末端不能等于1，只能无限逼近1，无法计算残余油饱和度，水相分流量曲线的末端值仍无法确定。

针对水相分流量拟合以及曲线末端含水饱和度取值的问题，以室内一维小岩心驱替实验为研究对象，根据水相分流量曲线的实际特征，结合水相分流量的实际物理意义及水相分流量在理论上的初始条件和边界条件，通过对比多种S型函数，确定并建立满足水相分流量的边界条件的全过程数学模型。该模型通过2 个调整指数，保障曲线S 型特征与实测水相分流量分布特征一致。同时，围绕水相分流量末端含水饱和度预测的问题，通过设置极限含水饱和度参数，实现利用实测资料拟合直接获得残余油饱和度。该方法利用相对渗透率测试报告即可实现残余油饱和度的预测，具有较为广泛的适用性。基于该模型可获得相对渗透率比值全过程曲线，能够明确驱替从初始时刻到极限时刻的油水运动规律变化特征，为开展水驱油藏开发动态研究，特别是高含水老油田注水开发动态特征研究和长期注水导致的油藏局部高耗水等问题的研究提供理论基础和指导。

1 水相分流量曲线

1.1 形态特征及物理意义

根据油藏工程理论，水相分流量的物理意义为任意位置的水相流量与油水两相流量之和的比值，反映油水两相流动中水相的流动能力［6］。水相分流量通常用fw表示，数值范围介于0 到1，函数表达式为：

（1）式表明，水相分流量与油水黏度比和油水相相对渗透率比值有关，对于特定油藏，油水黏度比可近似认为是定值，因此，水相分流量的大小和变化过程实质上反映了油水相相对渗透率比值随驱替过程的变化。由于油水相相对渗透率比值是含水饱和度的函数，水相分流量也是含水饱和度的函数（图1）。

图1 水相分流量理论曲线Fig.1 Theoretical curve of water fractional flow

大量室内实验及矿场开发实践表明，水相分流量曲线呈S 型，具有单调递增性质［7-8］。曲线形态反映了油水两相流量在不同驱替阶段的变化过程，初始阶段水相分流量较低，表明低含水期水相流速低，地层中流体以油相流动为主；进入中高含水期后，曲线大幅上升，此时水相流速逐渐上升，油相流速下降迅速；到了高含水阶段，曲线趋近平缓且逐渐接近于1，表明此时两相流体以水相流动为主，油相流动能力极低，驱替效果越来越差［9-11］。当fw=1 时，地层流体完全为水相单相流，油相不再发生流动，此时曲线对应的含水饱和度为残余油饱和度［12-13］。

1.2 边界条件

残余油是指被注入水或驱油剂波及仍驱替不出来的原油，这部分原油体积占地层孔隙体积的百分数即为残余油饱和度。对于室内一维小岩心驱替实验而言，注入水波及系数为1，因此，小岩心驱替的残余油饱和度是在注入量足够大甚至达到无穷大时出现。由于室内实验注入量有限，利用实验获取分流量末端含水饱和度是难以实现的。

从数学角度上，注入量趋近于无限大是存在的，水相分流量理论上可等于1，此时对应的含水饱和度为水驱油含水饱和度的极限值。同时，在注入水即将注入的时刻，岩心内尚未但即将发生流动，此时水相分流量为0，含水饱和度为原始含水饱和度，由此确定了水相分流量曲线的边界条件。

初始条件为：

极限条件为：

由于Sorw不确定，直接拟合fw与Sw关系具有多解性，为提高数学模型的精度，定义参数可采储量采出程度的物理意义为目前累积采出油量与可动油区间内地质储量的比值。其表达式为：

由于Sw∈[Swi,Sorw]，由（2）式和（3）式可知ηo∈[0,1 ]。将fw与Sw曲线转化成fw与ηo曲线，等同于对水相分流量曲线进行横向拉伸，纵轴不变，仍可以保持曲线形态及特征（图2）。

图2 fw与ηo关系曲线Fig.2 Relationship curve between fw and ηo

2 水相分流量曲线模型的建立

2.1 模型基础结构的确定

通过对水相分流量曲线边界条件的分析，将fw∈[0,1 ]，Sw∈[Swi,Sorw]的拟合问题转化成fw∈[0,1 ]，ηo∈[0,1 ]的问题，由于ηo取值范围明确，对数学模型的选择也更加严格。考虑待求曲线的S型特征，结合曲线定义域和值域均为[0,1 ]的特点，对目前较为常见的S 型曲线进行分析，目前较为常用的S型曲线模型［14-17］如表1所示。

目前大多数S型曲线的函数模型由于存在指数e，导致函数初始值不能取0，且极限值不能取1，与水相分流量曲线的初始条件和理论极限不符。这些函数大多可以用于拟合水相分流量曲线的中间区间，无法用于拟合包含初始值和极限值的全过程分流量曲线。多项式理论上只要阶数足够高，就可以表征任意复杂函数曲线，但考虑多项式的复杂程度，多项式次幂越高，求解越难，不利于实际应用。有理式具有端值可取、曲线可调的特征，能够满足水相分流量曲线的初始条件和极限条件。同时，针对不同类型的水相分流量曲线，有理式能够通过调整拟合指数，满足中间过程的拟合需要，因此，水相分流量的拟合模型采用有理式形式。

2.2 数学模型的建立

参考表1 中S 型曲线有理式的基本形式，令自变量x为可采储量采出程度，y为水相分流量。由于驱替极限条件fw=1，令Vmax=kn+1，建立水相分流量曲线的初始模型：

表1 常用S型曲线的数学模型及取值范围统计结果Table1 Statistics of common S-curve mathematical model and value range

根据（5）式的函数形式，函数的初始值为ηo=0，fw=0，而极限值满足条件ηo=1，fw=1，符合水相分流量曲线的边界条件。数学结构上，（5）式包含kn和ηon2个指数项，其中kn主要影响曲线初始阶段的形态，kn越小，曲线上升段向左偏移且上升速度越快（图3）。根据油藏工程理论，水油黏度比越低（即油水黏度比越高），水相分流量曲线的凸性越突出，表现为油相黏度大，水驱油见水后含水率上升快，水相分流量曲线上升迅速［18-20］。水油黏度比对分流量曲线的影响规律与数学模型中kn具有一致性。设油水黏度比为μR，令，将（5）式改写为：

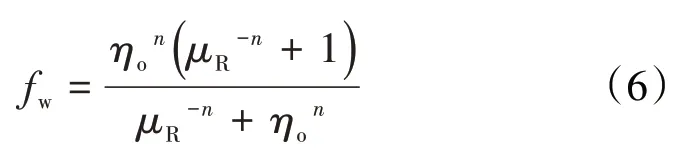
实际油藏开发中，即使油水黏度比相同，油水运动规律也会因储层物性及驱替条件的不同而存在较大差异，水相分流量曲线形态也存在不同。为保障模型的通用性和拟合精度，对模型指数项进行区分，将μR-n改写为μR-m，进一步提高模型在各种条件下的适用性。最终构建水相分流量基本函数式为：

由（7）式可知，改写后的数学模型仍满足水驱油过程的边界条件，主要表现为开始驱替时，ηo=0，fw=0；达到极限驱替条件时，岩石孔隙内无油相流动，采出端只出水，此时ηo=1，fw=1。对于特定油藏流体，油水黏度比可认为是常数；而拟合系数m和n，其主要作用是调整曲线的S 形态，使模型在处理不同类型水相分流量曲线均可达到较好的拟合效果。

将（4）式代入（7）式中，得：

（8）式反映了水相分流量与含水饱和度的关系，式中未知量包括m，n和Sorw，可通过拟合相对渗透率测试中水相分流量测试结果，从而得到理论极限驱替下的残余油饱和度。

根据（1）式，油水相相对渗透率比值的表达式为：

将（8）式代入（9）式，即可得到油水相对渗透率比值的全过程曲线。

3 应用实例

图3 相同n不同k的水相分流量有理式模型计算结果Fig.3 Calculation results of rational formula model under same n and different k values

胜利油田中高渗透油藏某砂岩样品孔隙度为0.34，渗透率为4.67 D，束缚水饱和度为0.18。在50 ℃条件下采用恒压驱替，注入水黏度为0.576 3 mPa·s，模拟油黏度为19.75 mPa·s。实验结束时注入量为1 000 PV，含水饱和度为0.728，剩余油饱和度为0.272。油水相相对渗透率及水相分流量测试结果如表2所示。

表2 胜利油田中高渗透油藏某砂岩样品高注入量相对渗透率测试结果Table2 Test results of relative permeability with high injection volume of sandstone sample from high permeability reservoir of Shengli Oilfield

利用（8）式对表2中的实验数据进行拟合，计算相对误差平均为0.4%，拟合精度极高，计算结果具有正确性和可靠性。模型的拟合系数分别为：m=2.29，n=4.61，Sorw=0.904，进而得到理论极限驱替的残余油饱和度为0.096，极限采收率为88.26%。

通过（8）式计算相对渗透率比值，对比实验测试结果（图4）可知，相对渗透率比值的拟合曲线与实测值具有较高的吻合度，表明建立的数学模型能够达到较好的拟合效果。由于模型考虑了极限条件，得到的相对渗透率比值曲线具有初始快速下降、中间近似直线段、末端下弯的特征，这一特征与现有油水运动规律的认识一致，表明模型具有可靠性。同时，相对渗透率比值曲线采用连续函数计算得到，使计算结果在数学和渗流2 方面的连续性均得到保障。

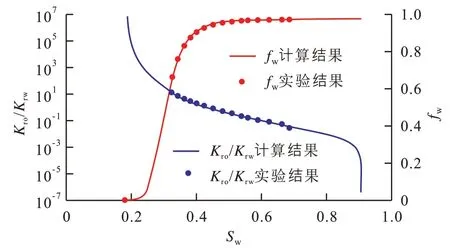
图4 水相分流量及相对渗透率比值拟合结果Fig.4 Fitting results between water fractional flow and relative permeability ratio

4 结论

基于油藏工程理论，利用数学方法建立了有理式形式的水相分流量全过程模型。相比以往的指数e 形式的模型，该模型考虑了水相分流量曲线的端点值，为水驱油残余油饱和度的确定以及采收率理论极限的预测提供了新的思路和方法。模型所需参数为相对渗透率测试报告，资料易获取，应用范围广泛，具有较高的普及性与实用性。但目前对该模型的认识尚浅，根据油藏工程理论，储层物性条件、流体性质条件及注采条件等因素发生变化，水相分流量曲线的形态也会随之改变。模型中调整曲线形态的参数为m和n，这2 个参数与实际物性、流体、注采等参数的关系及参数具体物理意义，还需要进一步开展研究。

符号解释

a,b,c,d,k,r,m,n——拟合系数；

fw——水相分流量，无量纲；

Kro——油相相对渗透率，无量纲；

Krw——水相相对渗透率，无量纲；

qo——油相流速，mL/min；

qw——水相流速，mL/min；

Sorw——残余油饱和度下对应的含水饱和度，无量纲；

Sw——含水饱和度，无量纲；

Swi——原始含水饱和度，无量纲；

Vmax——应变量的最大值，无量纲；

ηo——可采储量采出程度，无量纲；

μo——油相黏度，mPa·s；

μR——油水黏度比，无量纲；

μw——水相黏度，mPa·s。