多孔介质内水包油型乳状液非等温流动表征及敏感因素

卢 川，王亚青，王 帅，杨 烁，刘慧卿

（1.中海油研究总院有限责任公司，北京 100028；2.中国石油大学（北京）石油工程学院，北京 102249）

稠油热化学技术应用过程中，由于表面活性剂的注入，多孔介质内往往就地生成大量水包油型乳状液，从而改善高黏度原油流动性［1-3］。水包油型乳状液在多孔介质内的流动过程中，其温度将发生明显变化，而温度对水包油型乳状液中分散相黏度、分散相与连续相间界面张力等多个参数将造成显著影响［4-6］。因此，研究多孔介质内稠油水包油型乳状液的非等温流动对于描述乳状液运移规律至关重要。

目前，对于多孔介质中水包油型乳状液的渗流规律及渗流特征的描述主要基于由ALVARADO 等提出的本体黏度模型［7］、由MCAULIFFE 提出的乳滴阻滞模型［8］和由SOO 等提出的过滤模型［9］。中国部分学者在这些模型的基础上，通过考虑更多影响因素来实现对原有模型的修正［10-12］。但通过调研发现，目前水包油型乳状液滴在多孔介质中的运移和相关渗流表征模型，缺乏对温度作用的表征和描述，更缺乏对水包油型乳状液在多孔介质非等温流动过程中相关敏感性因素影响规律的分析和论证。

在对多孔介质进行简化的基础上，笔者以水包油型乳状液滴通过孔喉为研究对象，通过表征温度对分散相黏度和界面张力等参数的影响，描述多孔介质中稠油水包油型乳状液非等温流动过程，并研究相关敏感因素。

1 非等温流动模型建立

1.1 多孔介质简化模型

对于稠油油藏，储层岩石多为疏松砂岩，由颗粒支撑。将储层岩石颗粒假想为等径圆球，并将储层多孔介质的流动空间视为一系列在水平方向上分布的变径毛细管束。岩石颗粒的排列方式为：3个颗粒正相切排列形成的空间为喉道，6 个颗粒组成的内部空间为孔隙，上述喉道和孔隙构成岩石多孔介质的一个孔隙单元［13］。利用回归方法得到不同位置孔隙半径的表达式为：

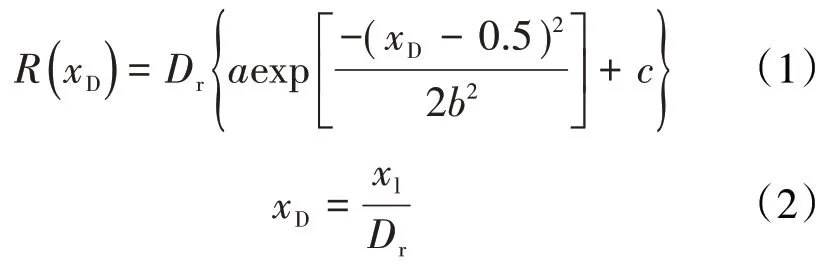
该模型的孔隙单元孔隙度为38%，小于等径颗粒理想排列孔隙度最大值47.6%，同时大于排列最紧密时的孔隙度25.9%，即满足实际情况。因此，在多孔介质中，孔隙介质颗粒按照如图1 所示的空间排布，则该多孔介质毛细管束和孔隙单元个数的表达式分别为：

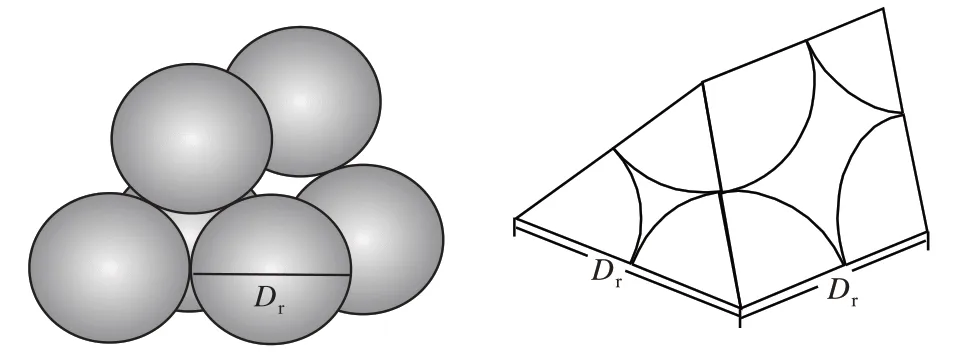
图1 多孔介质岩石等径颗粒排列Fig.1 Arrangement diagram of equal diameter particles in porous media rock

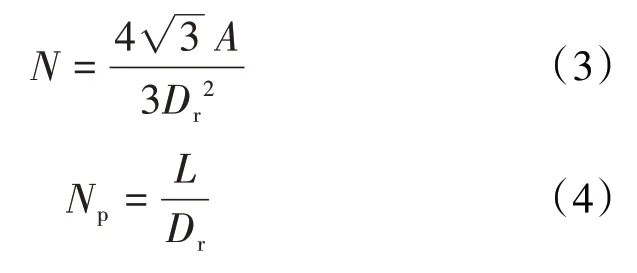
1.2 非等温流动温度分布

1.2.1 多孔介质沿程乳化实验

安装实验装置（图2），进行稠油热化学复合体系多孔介质沿程乳化实验，以模拟水包油型乳状液在多孔介质中的非等温流动。利用填砂管模型，充填介质是直径为100～120 μm 的玻璃微珠。采用稠油、蒸汽、表面活性剂溶液同时注入的方式，就地形成水包油型乳状液。复合体系总注入速度为3 mL/min，注入油水体积比为1∶1，蒸汽注入温度为300 ℃，表面活性剂质量分数为0.1%。对于注入水部分，按照蒸汽注入速度与表面活性剂溶液注入速度比为1∶1 进行分配。自入口端至出口端共设置5个压力采集点（测点之间距离为15 cm）和4 个温度采集点，并连接至数据采集系统进行数据自动收集。

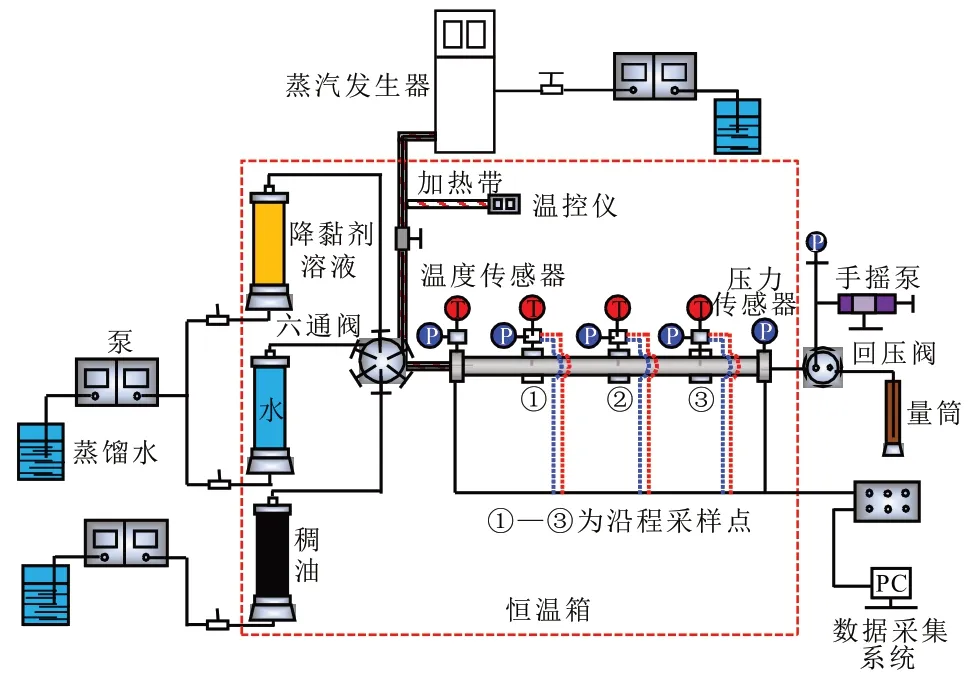
图2 稠油热化学复合体系多孔介质沿程乳化实验装置Fig.2 Experimental device for the in-situ emulsification process of porous medium of heavy oil thermochemical composite system

由沿程各测点温度和压力变化（图3）可以看出，在稠油热化学复合体系注入速度一定的条件下，随时间增加，各测点温度、压力逐渐升高。当多孔介质中乳状液的生成、截断、聚并和破碎达到平衡状态，乳状液粒径分布达到稳定状态的条件下，各测点温度逐渐趋于稳定，测点间温度差异基本保持不变。各测点压力稳定虽略有滞后，但最终也趋于稳定，测点间压力差异亦基本保持不变。改变实验参数（油水体积比为1∶4，蒸汽注入温度为200 ℃），同样出现乳状液流动达稳定状态时，各测点温度、压力差异保持不变的现象。

图3 多孔介质沿程各测点温度和压力变化曲线Fig.3 Variation curves of temperature and pressure at each measuring point along way in porous media

1.2.2 计算模型建立

由热流体注入过程中的热量传递方式（图4）可见，沿注入方向，如图4b 所示的x轴方向上，注入热量以渗流携热和导热2 种主要方式传递；y轴方向上，热量以对流方式进行换热。当乳状液流动达到稳定状态时，各测点温度趋于稳定，且不随注入时间的变化发生明显波动。因此，可以将以上热量传递方式简化为：注入热量一部分沿x轴方向通过孔隙介质内的连续相和乳状液滴进行传导，一部分沿y轴方向以对流换热向周围无限大介质散热。由于沿流动方向的温度变化更为明显，可近似认为多孔介质内的温度分布是沿x轴方向的一维稳态温度场。同时，为了反映y轴方向对流换热的散热量，根据能量守恒，将沿y轴方向的散热量作为多孔介质内沿x轴方向导热过程同时存在的负内热源［14］。因此，达到稳定状态时，乳状液在多孔介质中的非等温流动传热过程可以转化为含有负内热源的一维稳态导热过程。

在距离入口端x处取长度为dx的微元，dx内的对流换热量为：

由于多孔介质孔喉半径较小（图4a），在计算多孔介质温度分布时可将变径孔隙空间假想为等径圆柱体（图4b），则（5）式中的Lp为：

多孔介质连续空间微元段内热源强度为：

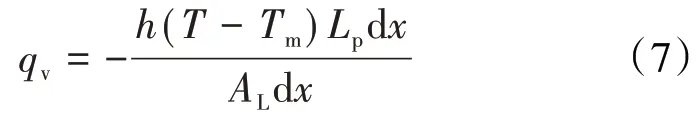
其中：

有内热源的稳态导热的能量方程可表示为：

则由（7）—（9）式可得：

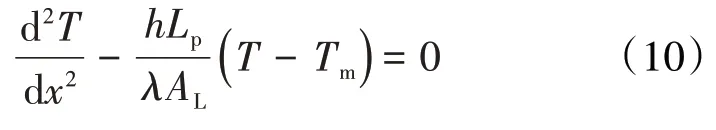
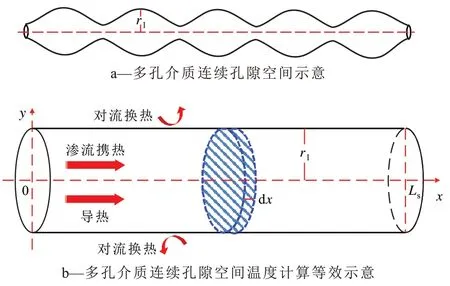
图4 多孔介质内导热过程温度分布计算示意Fig.4 Diagram of calculation of temperature distribution during heat conduction in porous media

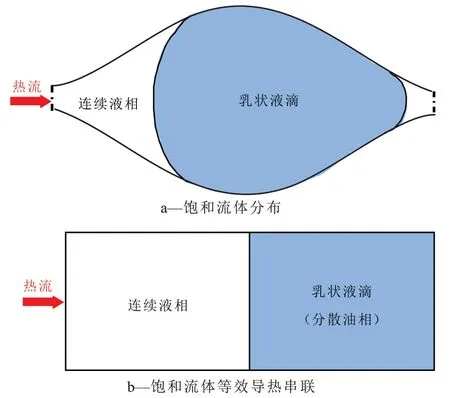
图5 多孔介质孔隙单元内饱和流体导热系数计算示意Fig.5 Diagram of calculation of thermal conductivity coefficient of saturated liquid in pore unit of porous media

对于单个液滴运移达到平衡状态的乳状液而言，假定其连续相和乳状液滴在多孔介质孔隙单元中的分布如图5a 所示。在乳状液滴存在区域内分散油相为主要饱和介质，忽略该区域内界面膜和部分连续液相对导热系数的影响。借此饱和流体导热系数计算模型可简化为连续液相和分散油相的串联模型（图5b）。根据导热系数串联模型计算方法［15-16］，可得：

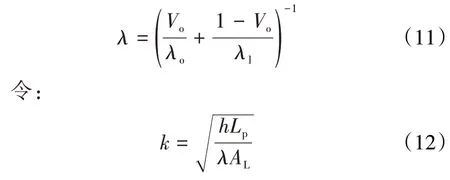
则（10）式可化简为：

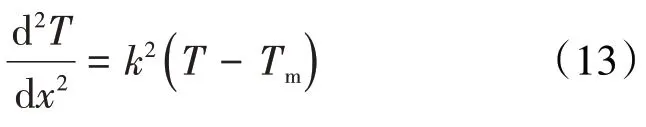
多孔介质连续孔隙空间的入口端和出口端边界条件可分别表示为：

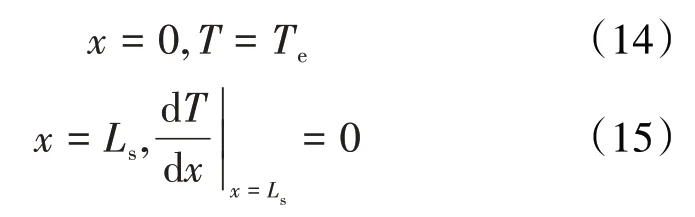
若利用以周围介质温度为基准的过余温度来表示沿程温度，则（13）式可转换为：

联立（13）—（17）式，可得沿流动方向距离入口端x处的温度为：

1.3 非等温流动压力分布

当就地乳化达平衡状态时，多孔介质内沿程压力分布也趋于稳定。由于连续液相和乳状液滴同时存在，因此需要对连续液相区和乳状液滴存在区的压力分布分别进行计算。孔隙单元内连续液相与乳状液滴流动形态如图6所示。

图6 孔隙单元内连续液相与乳状液滴流动形态示意Fig.6 Schematic diagram of continuous liquid and emulsion droplet flow patterns in pore unit

1.3.1 连续液相区压力计算

在连续液相区，连续相流体流动时受到壁面作用的剪切应力。对于水包油型乳状液，连续相流体的黏度受温度影响较小，为牛顿流体，因此根据动量守恒定律，对于连续液相区的连续相流体可得：

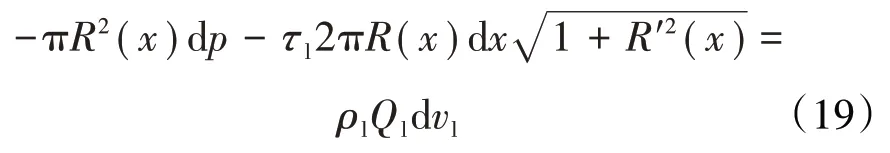
利用表征实际流体运动微分方程的纳维-斯托克斯方程，得到毛细管中连续液相微元运移速度与作用压力的关系式为：

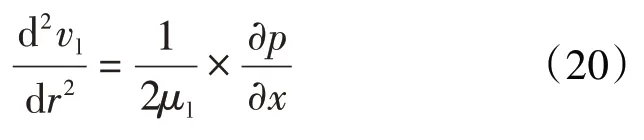
多孔介质孔喉空间中心流线及孔喉壁面的边界条件分别为：

由（20）—（22）式可得：

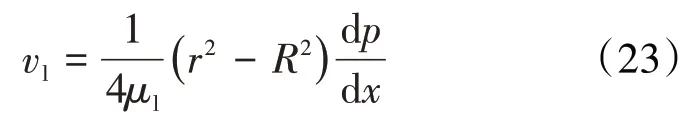
多孔介质孔隙单元内连续液相流量为：

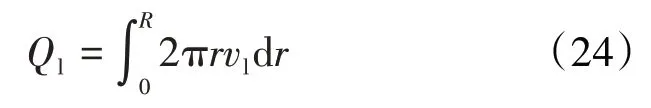
则由（23）和（24）式可得：

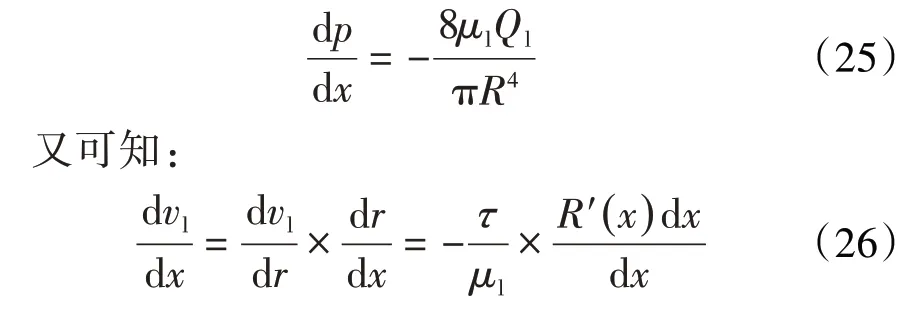
在r=R处则：

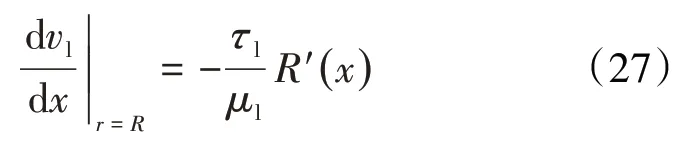
将（25）式和（27）式代入（19）式，即可得到连续液相区多孔介质壁面对连续相流体的剪切应力为：

1.3.2 乳状液滴存在区压力计算

在乳状液滴通过毛细管孔道过程中，毛细管壁面和内核油滴表面均将对液膜移动施加阻力。由于水包油型乳状液内部包裹的是稠油油滴，其黏度受温度影响较为明显，而黏度将影响液滴变形和壁面滑移，同时对液滴变形起抑制作用［17-18］。在不考虑乳状液滴破碎的条件下，内相油滴黏度越大，乳状液滴变形越难。因此，需要将黏度对乳状液滴流动的影响考虑在内。

根据动量定理可知：

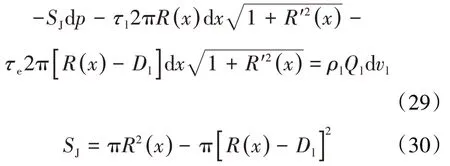
由于R＞＞Dl，则：

目前实验研究结果表明，液体层间会出现滑移现象，不同尺度流动系统条件下的滑移系数不同［19-21］。流动系统特征尺度为250～800 μm 时，滑移长度系数为2～8 μm。此外，温度越高，液体黏度越小，界面上的流体更易流动，即容易发生界面滑移。为表征乳状液滴黏温特性对滑移的影响，引入滑移系数来描述连续相液膜在油相液滴表面的相对运动。滑移系数定义为：

其中：

乳状液滴存在区液膜移动过程中多孔介质孔喉壁面处及孔喉-液膜厚度处的边界条件分别为：

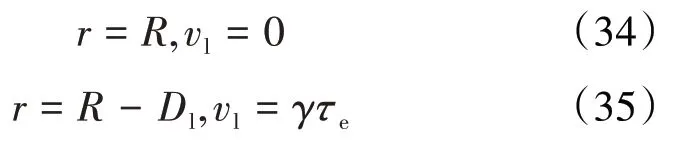
根据（34）和（35）式，对（19）式积分得：

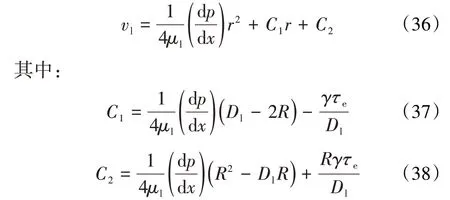
整理得：

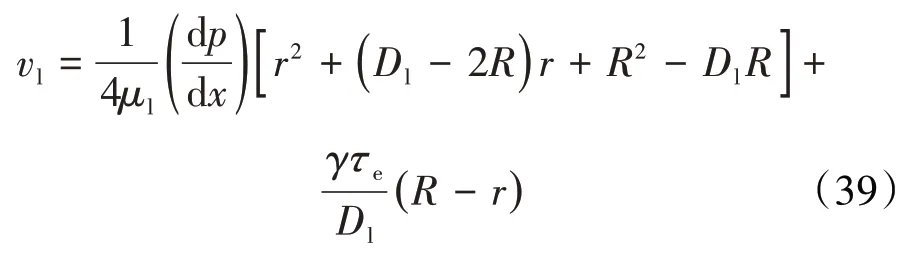
乳状液滴存在区连续相流量为：

由（39）和（40）式可得：

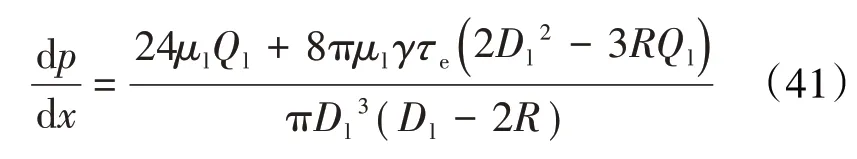
对（41）式省略高阶项进行化简，得：

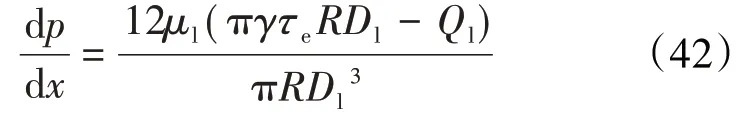
由于在乳状液滴存在区连续液相满足牛顿层流理论，因此，将（28）式和（42）式代入（30）式中，可得：

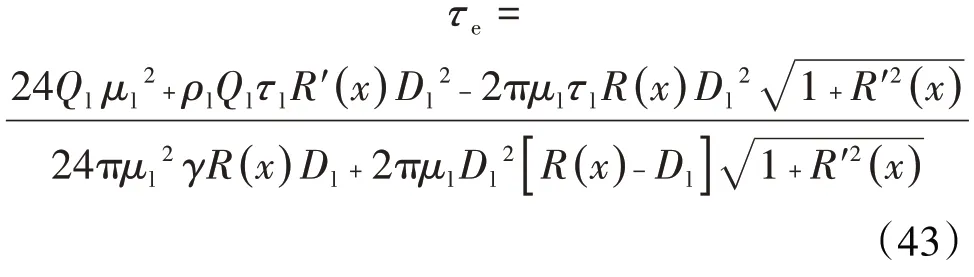
1.3.3 多孔介质孔隙单元压差计算

多孔介质内孔隙单元受力状况如图7所示。

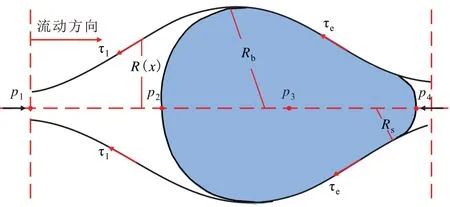
图7 孔隙单元内连续液相与乳状液滴受力状况Fig.7 Force analysis of continuous liquid and emulsion droplets in pore unit

根据连续液相区和乳状液滴存在区的压力分布可知：

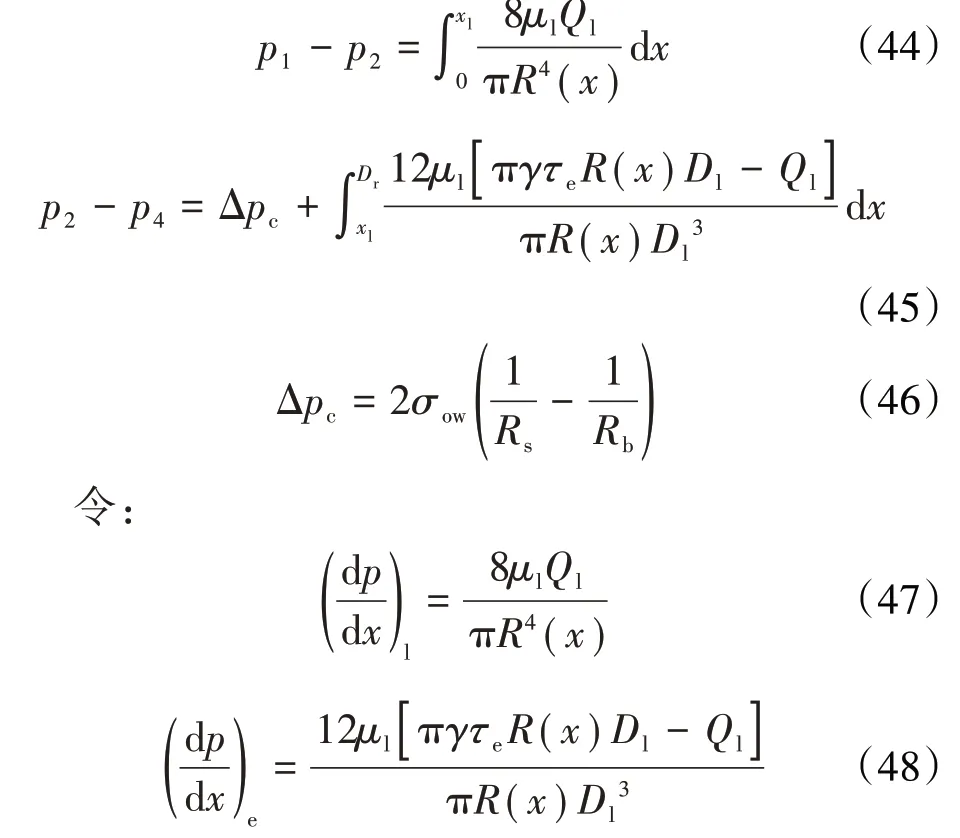
则多孔介质孔隙单元两端压力差为：

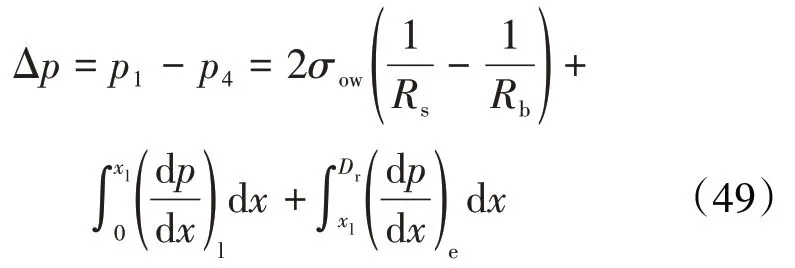
由于界面张力与温度基本呈线性关系［22-23］，因此其关系式可表示为

1.3.4 连续多孔介质内压力计算

当多孔介质内乳状液滴的运移达稳定平衡状态，乳状液滴在多孔介质中的粒径大小趋于稳定和均一，每个孔隙单元内的连续液相分布和乳状液滴分布也趋于一致。以图8 中排列方式为例，若已知多孔介质入口端压力，则多孔介质内第i个完整孔隙单元末端（即xi处）压力可表示为：

图8 多孔介质内连续液相与乳状液滴相对位置示意Fig.8 Relative position of continuous liquid phase and emulsion droplet in porous media

若xi之后任意一点xj（满足xj∈（xi，xi+1））位于连续液相区，则：

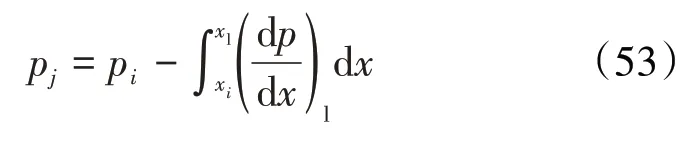
若满足xj∈（xi，xi+1）且位于乳状液滴存在区，则：

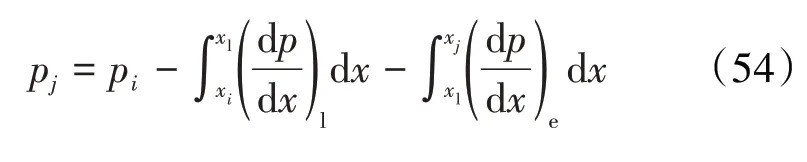
2 计算模型的实验验证

实验所用稠油的黏度随温度变化拟合曲线如图9a 所示。按照不同温度下黏度变化趋势，得到（31）式中的拟合参数m和n，当小于100 ℃时其值分别为286 535 和-0.072，当大于100 ℃时其值分别为1 908 和-0.024。由稠油与表面活性剂溶液界面张力随温度变化拟合曲线（图9b）得到（50）式中的拟合参数e和f分别为-0.000 6和0.19。

在表面活性剂质量分数为0.1%、油水比为1∶4以及蒸汽注入温度为200 ℃的条件下，利用温度和压力实验测量结果，根据多孔介质沿程温度和压力计算公式，将实验结果与计算结果进行对比（图10）。整体来看，不同注入条件下计算结果与实验结果均呈现出较好的一致性，表明在多孔介质简化模型的基础上，以单个乳状液滴通过喉道为研究对象，引入温度对内核油相黏度和界面张力的影响，进而描述稠油乳状液在多孔介质中的非等温流动过程是合理的。

图9 黏度/界面张力随温度变化曲线Fig.9 Variation curves of viscosity/interfacial tension with temperature

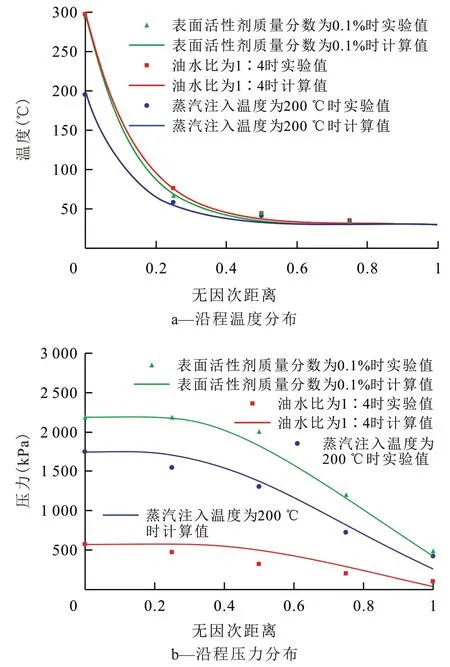
图10 不同注入条件下沿程温度/压力分布实验结果与计算结果对比曲线Fig.10 Comparison curves of experimental results and calculated results of temperature and pressure distributions along way at different injection conditions

3 非等温流动敏感因素

3.1 蒸汽注入温度

通过改变蒸汽注入温度（140，180，220，260，300 ℃）研究其对乳状液运移过程中沿程温度和压力变化的影响。由计算结果（图11）可知，随注入温度的降低，入口端压力逐渐增大，沿程压力下降平缓段与快速下降线性段的转换位置向入口端移动。在入口端附近，不同高温条件对稠油的加热程度相似，乳状液滴内核油相黏度相近。随运移距离的增加，在相同热损失条件下，低注入温度的沿程热传播距离减小，内核油相黏度增大，对连续液相的剪切力增强，整个乳状液滴通过孔喉的阻力增大，致使沿程压力梯度增大。当运移距离继续增加后，由于不同蒸汽注入温度的沿程温度分布已趋于一致，且均处于较低水平，乳状液滴性质相似，因此在此区域内压力梯度基本相同。

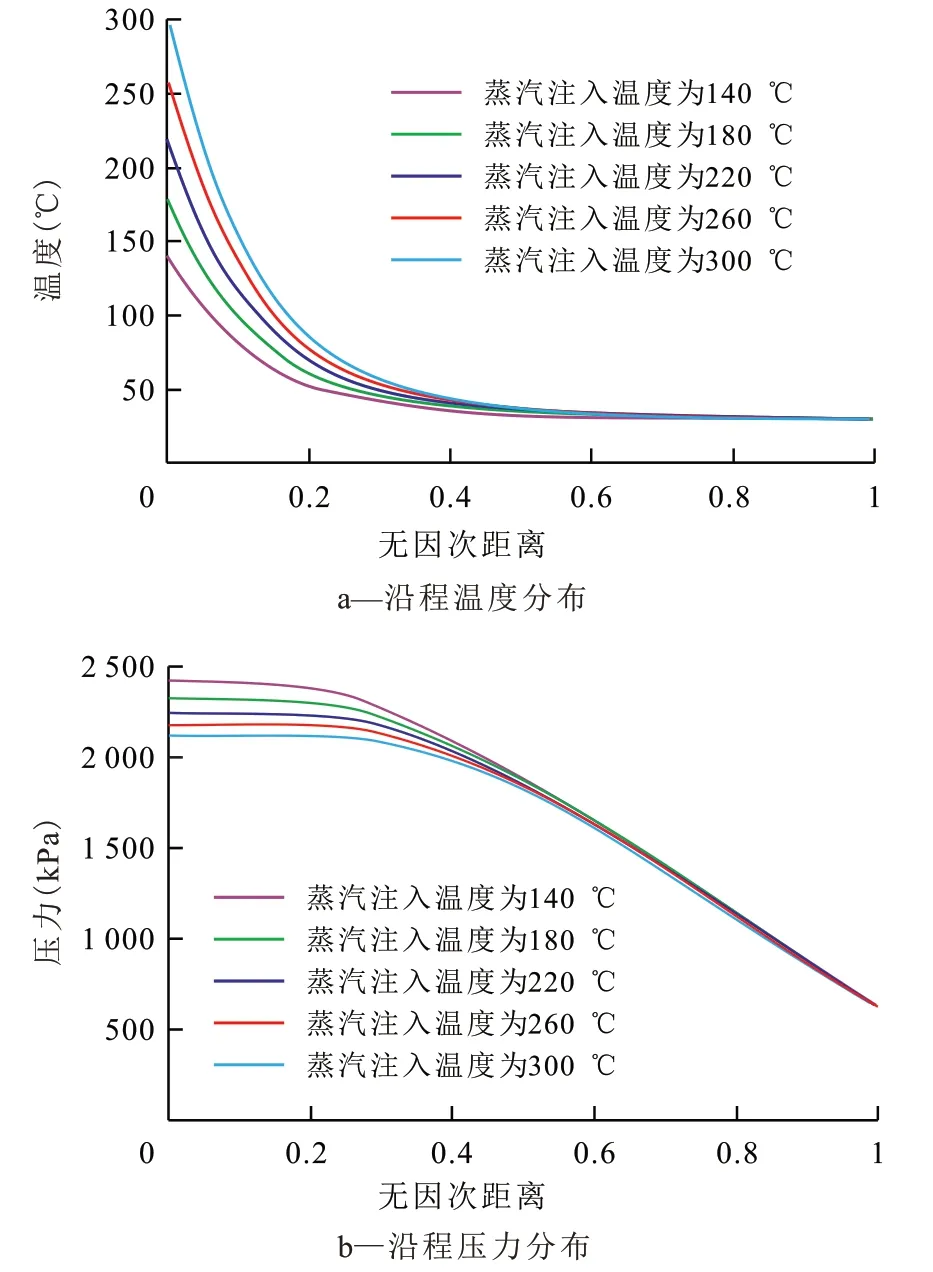
图11 不同注入温度条件下沿程温度和压力分布计算结果Fig.11 Calculation results of temperature and pressure distributions along way at different injection temperature conditions

3.2 分散相黏度

选取25 ℃下3 种黏度（168 150，50 910，10 688 mPa·s）的稠油进行模拟计算，得到稠油黏度随温度变化曲线（图12）。根据石油烃类混合物的导热系数计算公式及部分文献中的实验结果［24-26］，目前对于稠油黏度与其导热系数的对应关系虽没有统一定论，但测试数据大致体现出随胶质和沥青质含量增加，原油黏度增大，同一温度下原油导热系数减小的趋势，且导热系数随温度升高而逐渐降低，但变化幅度及范围很小。因此，将分散相稠油的导热系数视为定值。通过改变分散相稠油黏度来研究其对乳状液运移过程中沿程温度和压力变化的影响。

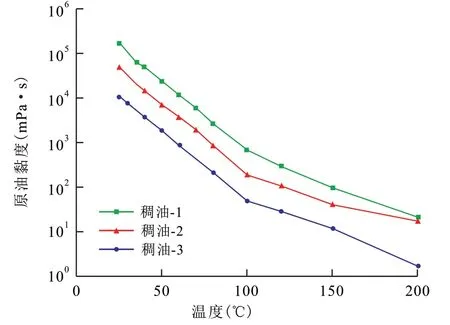
图12 不同稠油黏温关系曲线Fig.12 Variation of viscosity with temperature for different heavy oil samples

在计算过程中，稠油-1、稠油-2、稠油-3的导热系数分别取0.1，0.15 和0.2 W/（m·K）。由沿程温度和压力计算结果（图13）可知，尽管不同黏度稠油的导热系数不同，但由于差异程度较低，其对温度的变化及沿程压力分布影响较小。分散相黏度主要影响低温区乳状液滴通过多孔介质孔喉的压力梯度。分散相黏度越大，乳状液滴通过孔喉所需的压力梯度越大，最终导致注入端压力越高。

3.3 分散相体积分数

不同油水比条件下，若稠油全部以O/W 型乳状液形式存在，则油水比对稠油乳状液非等温流动的影响实质是分散油相体积分数的影响。由多孔介质内饱和流体导热系数串联计算模型可知，分散相与连续相不同的配比关系将影响饱和流体的总导热系数。设定不同分散相体积分数条件下所形成的乳状液滴粒径相同，通过改变分散相体积分数（10%，20%，30%，50%，70%）来研究其对乳状液运移过程中沿程温度和压力变化的影响。由计算结果（图14）可见，随分散相体积分数的增加，沿程温度下降加快，入口端压力逐渐升高。在无因次距离大于0.5 的区域，沿程温度和压力分布差异较小。由于油相导热系数低于水相导热系数，随着分散油相体积分数的增加，饱和流体总导热系数逐渐降低，沿程导热能力下降，热损失增大，同时造成分散油相黏度增大，通过多孔介质孔喉处阻力增加。叠加的效果即造成入口端压力随分散相体积分数的增加呈上升趋势。

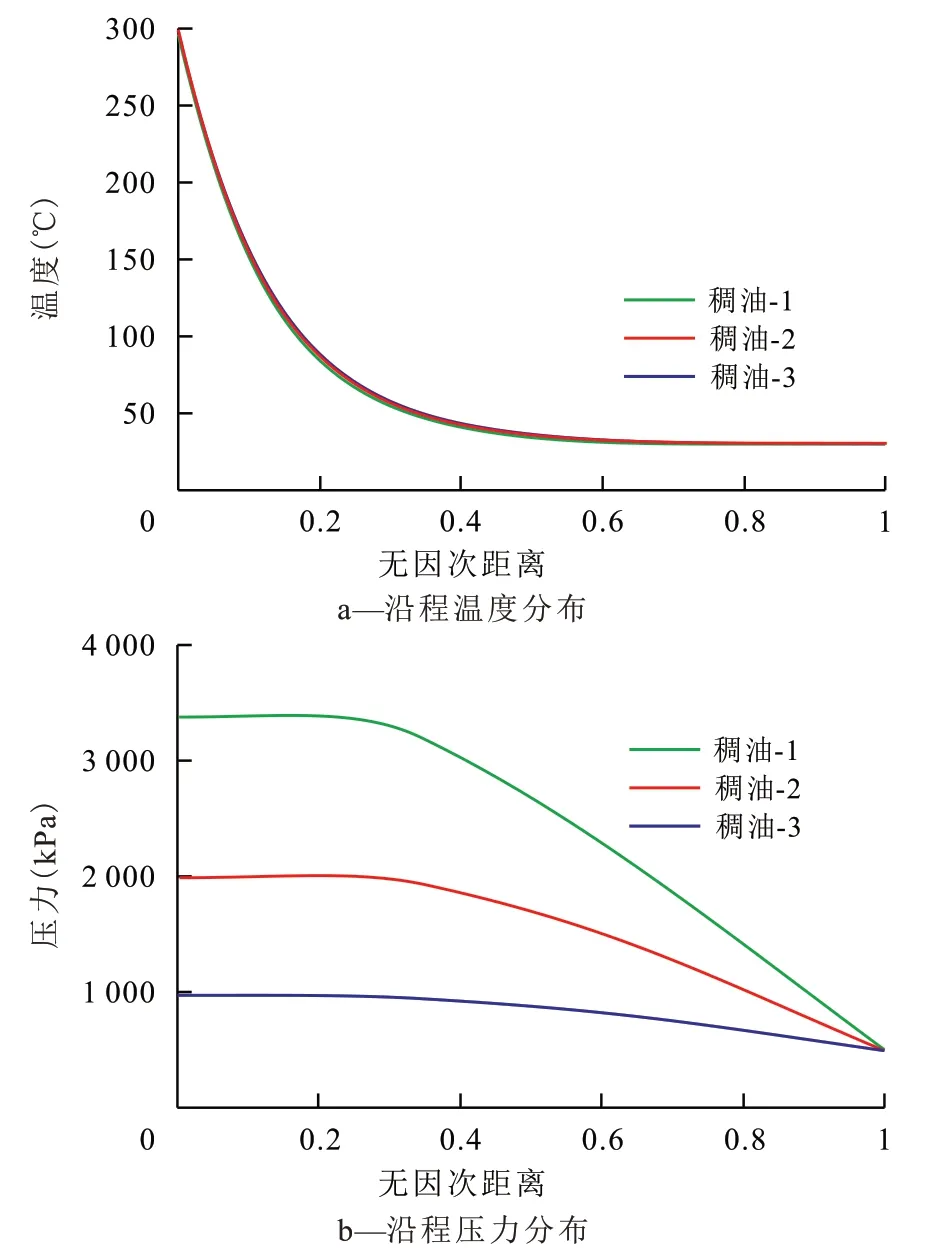
图13 不同分散相黏度沿程温度和压力分布计算结果Fig.13 Calculation results of temperature and pressure distributions along way for dispersionphases with different viscosities

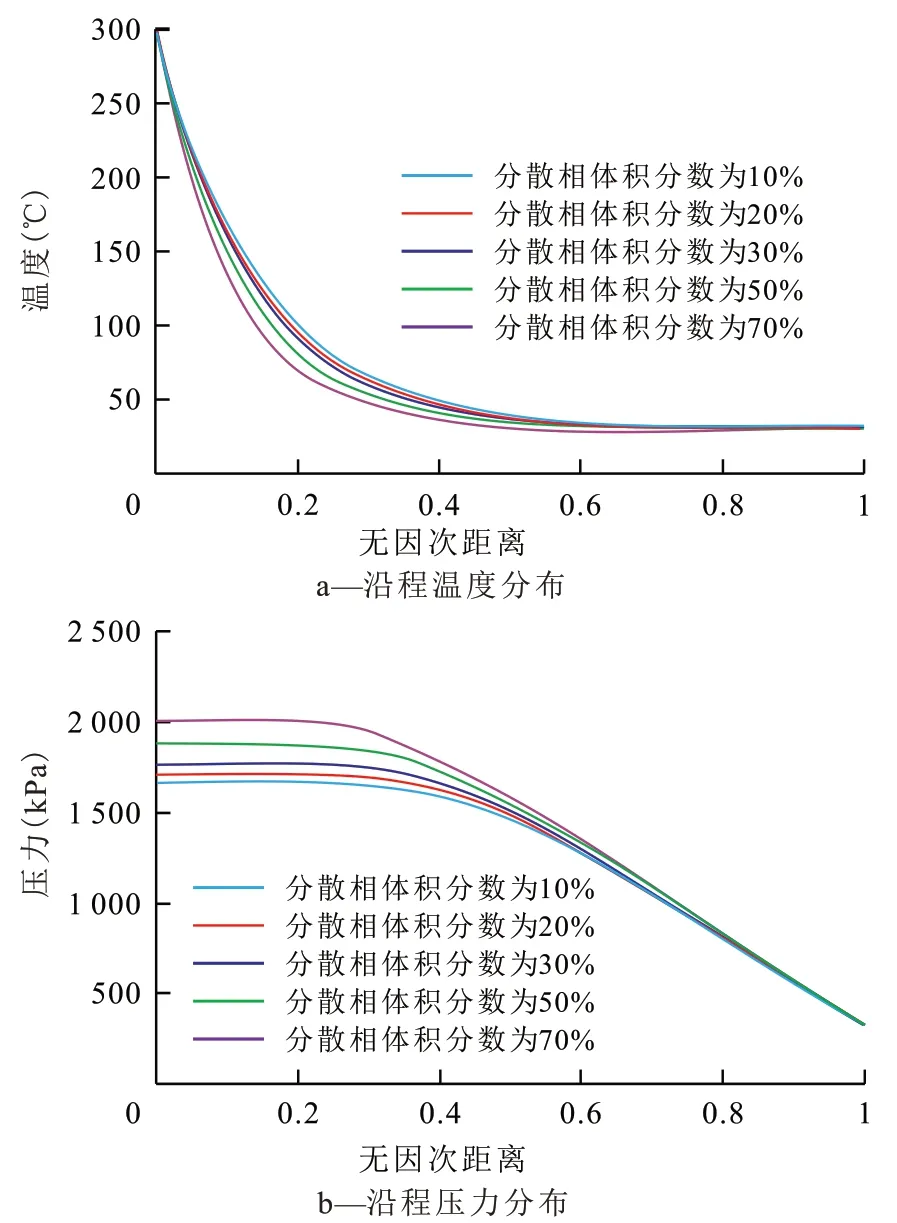
图14 不同分散相体积分数条件下沿程温度和压力分布计算结果Fig.14 Calculation results of temperature and pressure distributions along way for dispersion phases with different volume contents

4 结论

实验条件下，就地形成的水包油型乳状液在多孔介质运移过程中，其粒径分布达到稳定状态时，水包油型乳状液在多孔介质中的非等温流动传热过程可以认作是含有负内热源的一维稳态导热过程。

在将多孔介质简化为变径毛细管束模型的基础上，利用导热系数串联模型计算饱和流体的总传热系数，同时考虑温度变化对分散相黏度及界面张力的影响，通过动量定理推导出连续液相区、乳状液滴存在区、多孔介质孔隙单元以及连续多孔介质的沿程温度和压力计算模型。实验证明，该计算模型是合理的。

随注入温度的降低，注入端压力逐渐增大，沿程压力下降平缓段与快速下降线性段的转换位置向入口端移动；分散相黏度越大，乳状液滴通过孔喉所需的压力梯度越大，入口端压力越高；随分散相体积分数的增加，沿程温度下降加快，入口端压力逐渐升高。

符号解释

a，b，c——回归系数，其值分别为0.23，0.19，0.11；

A——横截面面积，μm2；

AL——等径圆柱体横截面面积，μm2；

Dl——液膜厚度，μm；

Dr——岩石颗粒直径，μm；

e，f——常数，由实验结果回归确定；

h——多孔介质与周围介质之间的表面传热系数，W/（m2·K）；

L——多孔介质毛细管束长度，μm；

Lp——多孔介质的周边长度，m；

Ls——等效多孔介质沿程总长度，m。

m，n——回归系数；

N——多孔介质毛细管束，无因次；

Np——孔隙单元数，个；

p——毛细管力，Pa；

p1——孔隙单元入口端压力，kPa；

p2——流动方向上连续液相与乳状液滴接触处压力，kPa；

p3——乳状液滴内部压力，kPa；

p4——孔隙单元出口端压力，kPa；

pi——多孔介质内第i个完整孔隙单元末端（即xi处）压力，kPa；

pj——多孔介质内2个完整连续的孔隙单元中任一点压力，kPa；

pin——多孔介质入口端压力，kPa；

pout——多孔介质出口端压力，kPa；

Δp——孔隙单元两端压力差，MPa；

Δpc——乳状液滴通过孔隙喉道产生的毛细管力，N；

qv——热源强度，W/m3；

Ql——连续液相流量，m3/s；

r——多孔介质孔喉半径，μm；

r1——等效多孔介质半径，m；

R——孔隙单元内不同位置孔隙半径，μm；

Rb——孔隙单元内乳状液滴较大弯曲液面的曲率半径，μm；

Rs——乳状液滴较小弯曲液面的曲率半径，μm；

SJ——乳状液滴存在区连续相液膜的横截面积，μm2；

T——微元内的温度，℃；

Te——入口端温度，℃；

Ti——第i个孔隙单元内温度，℃；

Tm——周围介质温度，℃；

vl——连续液相在毛细管中的运移速度，m/s；

Vo——油相的体积分数；

W——微元dx内的对流换热量，W；

x——距入口端某处，m；

xl——孔隙单元一定位置处距起点的距离，μm；

xD——无因次距离，其值为孔隙单元一定位置处距起点的距离与岩石颗粒直径之比；

xi——第i个完整孔隙单元距入口端距离，m；

xj——第i个和第i+1 个孔隙单元之间任意一点距入口端距离，m；

y——等效多孔介质孔隙半径，m；

γ——滑移系数；

ε——滑移长度系数，μm；

θ——周围介质温度为基准的过余温度，℃；

λ——孔隙单元内饱和流体的导热系数，W/（m·K）；

λo，λl——油相和连续液相的导热系数，W/（m·K）；

μl——连续液相黏度，Pa·s；

μoi——第i个孔隙单元内乳状液滴内核油相的黏度，mPa·s；

ρl——连续液相密度，kg/m3；

σiow——多孔介质内第i个完整孔隙单元内油水界面张力，N/m；

σow——油水界面张力，N/m；

τl——连续液相区壁面对连续液相的剪切力，Pa；

τe——油滴表面对连续相液膜施加的流动阻力，N/m。