简支小箱梁桥横向应力分布模型试验研究
周思源
中铁十八局集团第五工程有限公司 上海 200444
道路桥梁的建设对于经济的增长有很大的促进作用,但人们对道路桥梁从多方面提出了更高的要求,比如行车时的舒适度、桥梁的耐久性和安全性等。
从受力性能、外观和经济上看,简支小箱梁桥有很大的优点,因此,在近年来的桥梁建设中,小箱梁桥的使用越来越广泛[1-5]。针对小箱梁桥的受力特点,我国学者展开了多方面、大规模的研究。
余泉[6]改变传统的简支T梁桥体系的刚接板梁法荷载横向分布理论及平面分析方法,研究和探讨小箱梁桥的受力行为以及设计计算方法;刘晓鸣等[7]以某一装配式小箱梁桥为例,利用不同的计算方法分别对其进行荷载横向分布的计算,同时根据梁格理论建立空间有限元模型进行验算;钟小军[8]以某装配式小箱梁桥为例,发现刚接板梁法及空间有限元法计算的结果和实测结果较为接近;钱寅泉等[9]采用空间有限元法对小箱梁的荷载横向分布系数进行了研究;陈翠丽[10]借助桥梁专业分析软件Midas Civil,对结构进行空间梁格分析,得到了横向分布系数;钟亚丽等[11]根据带翼小箱梁桥的特点,对提出的理论与刚接板法和铰接板法计算以及实桥的试验结果做对比,认为对于未设置横隔板的小箱梁,采用铰接板法计算横向分布系数较为合理;杨美良等[12]运用Ansys软件研究不同斜交角度下小箱梁跨中荷载横向分布影响线以及荷载横向分布系数的变化规律,并以实际桥梁进行验证。
上述研究多采用理论分析或者有限元建模的方法研究小箱梁桥的受力特点和横向分布规律,制作模型模拟实际工程的研究较少[13-15]。
因此,本文基于上述研究基础,采用有机玻璃制作小箱梁桥模型,研究在不同工况下梁的横向应力分布,为实际工程提供理论指导。
1 试验方案设计
1.1 模型制作
本次试验以某实际小箱梁桥为工程背景,按照1∶20制作无内横梁的简支小箱梁模型。模型材料为有机玻璃,其弹性模量为2 800 MPa,泊松比为0.35。选取有机玻璃作为模型材料是由于其具有高强度、低成本特性,且本次试验主要测量跨中挠度和应变,这2个参数同时也是实桥模拟主要参数,经过换算后能够满足相似原则。模型全长1.5 m,宽度0.62 m,模型的横截面尺寸如图1所示。试验设备及加载方式如图2所示。

图1 小箱梁模型横截面示意

图2 试验设备与加载方式
1.2 工况设计及加载
试验采用标准质量的砝码对模型施加荷载,加载时先放1个砝码,待稳定后再接着放下一个,加载控制值为60 kg。
设计8种不同的加载工况,沿横向加载点为1号梁和2号梁的中心处,沿纵向则为桥长的1/8、1/4、3/8和1/2处。其中梁横向坐标的原点为图中1号梁最左端点处,向右为坐标正向,不同的加载工况见表1。
在4个截面的位置布置应变和挠度测点,以测定模型在不同加载工况下的应变和挠度。采用提前安装好的应变仪和百分表读取模型的应变和挠度。加载之前粘贴应变片,设置好挠度测定装置,并将仪表归零。加载完成后,待模型的变形完全稳定时测记读数,然后分步撤去砝码,进行下一个工况的加载,并重复以上操作。
2 试验结果分析
根据应变仪和百分表获得的数据,分别进行小箱梁在不同加载工况下的横向分布规律研究。其中挠度由百分表获得,并在此基础上假设梁受力大小和梁的挠度成正比,从而得到梁荷载横向分布的规律。
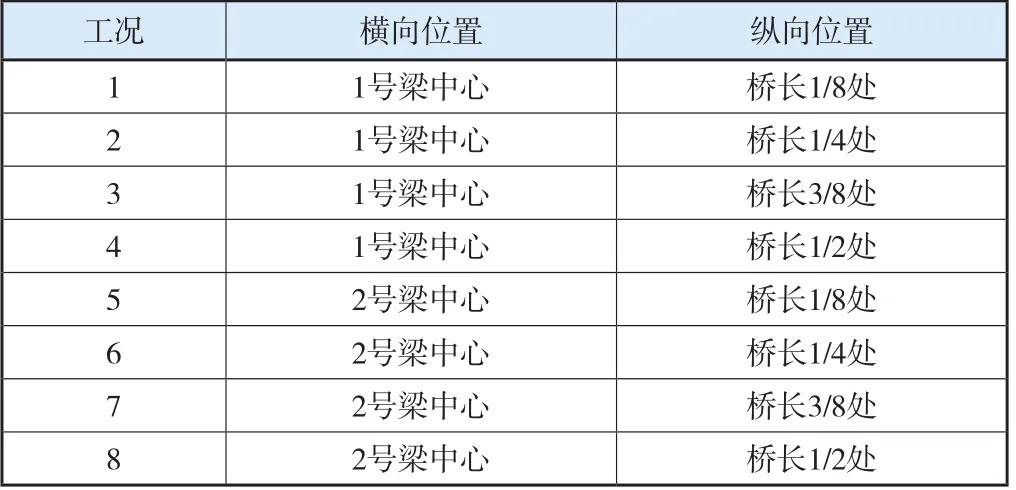
表1 不同的加载工况位置
2.1 小箱梁的挠度分析
小箱梁在砝码施加的集中荷载下产生一定的挠度,在不同的位置处加载并通过预先布置的测定仪器获得不同位置处小箱梁的挠度大小。图3展现了在不同工况下,小箱梁中间截面部分挠度大小随横向位置的变化规律。

图3 不同工况下小箱梁挠度分布规律
由图3可以看出,在工况1—4下,随着横向位置的增大梁的挠度减小,即越远离荷载作用的位置,小箱梁的挠度越小。但不同的工况下,挠度减小的幅度不一致,其中工况4的变化幅度最大,工况1的变化幅度最小。对比4条曲线可以发现,从工况1到工况4,小箱梁的挠度逐渐增大,工况4的挠度整体上变化最大。在工况5—8下,小箱梁的挠度沿横向分布相对均匀,在横向20 cm处曲线均下凹。工况5—8相比于工况1—4,梁的受力情况更合理,产生的挠度相对较小。
2.2 小箱梁的挠度影响线分析
为了便于分析和比较,将不同测点处梁的挠度代数和化为1。以横向位置为横坐标,单片梁挠度值与各片梁挠度值之和的比值为纵坐标做出不同工况下跨中截面处的影响线竖标值,如图4所示,由影响线可推算荷载横向分布规律。由图4可以看出,挠度的分布差别很小,越靠近荷载作用的地方,梁的挠度越大。
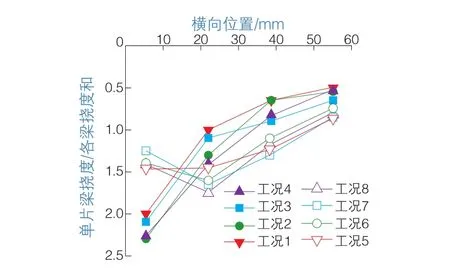
图4 不同工况下小箱梁影响线
2.3 小箱梁内力分析
通过粘贴的应变片可以获得不同工况条件下,小箱梁在4根梁处产生的应变,并假设小箱梁处于弹性阶段,将应变乘上弹性模量获得小箱梁在对应位置的应力大小,再乘上对应截面的截面模量即可获得其弯矩。绘制工况4和工况8条件下,荷载在不同截面处产生的弯矩随梁号的变化规律图(图5)。
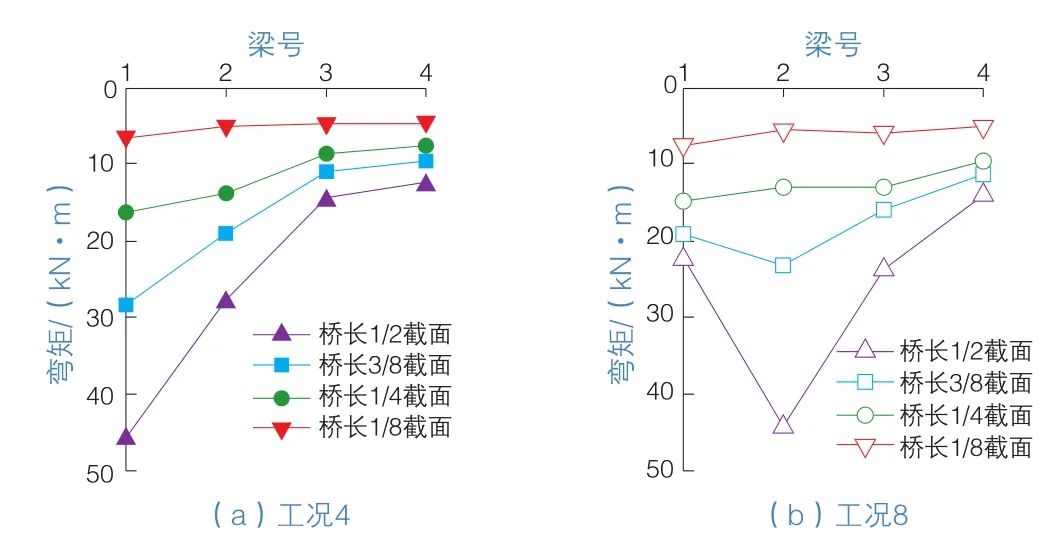
图5 工况4与工况8不同截面位置处弯矩横向分布
由图5可以看出,在工况4和工况8条件下,桥长1/8截面处梁的弯矩横向分布均匀,几乎呈一条直线,且其大小相近,说明离荷载作用位置越远的地方,梁的弯矩分布越均匀,且其值也越小。荷载作用于1号梁中间截面时,弯矩随着梁号的增大而减小,弯矩的变化规律近似呈线性变化,其中1号梁的弯矩最大;而当荷载作用于2号梁中间位置时,2号梁中间截面处的弯矩最大。可以看出,小箱梁承受的弯矩由不同的梁承担,但弯矩的分布不够均匀和合理,可考虑在小箱梁的中间增设内横梁,使弯矩传递到相邻的横梁上,从而使小箱梁的受力更加合理、更加均匀。
3 结语
通过模型试验测得的数据分析发现:
1)远离荷载作用的位置,小箱梁的挠度减小,不同工况下,挠度减小的幅度不一致。
2)荷载作用附近的挠度和弯矩分布不均匀,距作用点越远,梁的受力情况越合理。
3)可通过在小箱梁桥的中间增加内横梁以改善其受力情况,提高其承载能力。

