场发射电推力器的参数选择与调控方法
刘子健,沈岩,*,耿金越,刘旭辉,秦宇
1. 北京控制工程研究所,北京 100190 2. 先进空间推进技术实验室,北京 100190 3. 北京市高效能及绿色宇航推进工程技术研究中心,北京 100190
近年来,微纳卫星由于其微小尺寸、低成本、短研发周期等特点,在一系列空间应用中得到快速发展,立方星是其中的一个典型应用。单组元的立方星尺寸为10 cm ×10 cm ×10 cm,质量在1 kg以内[1]。随着立方星的不断发展,针对立方星的微推进系统研究也相应展开。场发射电推力器由于其微小化、高比冲、低功耗、精确推力可调等特点,非常适合用作微小卫星,特别是立方星的高精度姿态控制,因此近年来得到广泛的关注和研究。与此同时,场发射电推力器在空间引力波探测等先进空间科学任务中也可以得到应用。由于应用前景良好,场发射电推力器逐渐成为近年来微推进领域的研究热点。
目前国内外针对场发射电推力器展开了广泛的研究,通过对已报道出的推力器产品的性能进行调研分析,可看出根据发射的带电粒子的荷质比不同,场发射电推力器具有不同的发射模式,可分为液滴模式、射流模式和离子模式。推力器的推力性能主要受其发射模式的影响。其中由液态金属铟/镓/铯等作为推进剂的场发射电推力器被称为FEEP,其发射粒子为金属离子,处于纯离子发射模式;由高电导率的电解质溶液(如甲酰胺的盐溶液)作为推进剂的场发射电推力器被成为胶体推力器,发射粒子由带电液滴组成,可工作在液滴模式或射流模式;由离子液体作为推进剂的场发射电推力器被称为离子液体电推力器,发射粒子中可存在带电液滴或带电离子,可工作在3种不同模式下。
典型的胶体推力器如美国Busek公司的CMNT产品,该推力器工作过程中产生体积较大的带电液滴[2],推力器的比冲只维持在较低范围。典型FEEP推力器如奥地利Enpulsion公司的使用液态金属铟作为推进剂的IFM Nano Thruster。该推力器工作过程中产生的为带电金属离子,在最大推力工况下,推力器比冲可达2 000~2 500 s;当推力相对较低时,可达到高于4 000 s的比冲值[3]。美国Accion公司研制了一种应用于立方星的微小化/模块化离子液体电推力器iEPS,采用离子液体EMI-BF4作为推进剂,其发射粒子由带电液滴和带电离子组成,比冲在1 000 s上下[4]。其中离子液体由于其高电导率、低饱和蒸汽压、可产生不同种类的发射粒子等优势,近年来得到广泛的研究,目前北京理工大学、上海交通大学、西北工业大学、北京机械设备研究所等中国高校和单位均针对离子液体电推力器展开了相关试验研究,并研制了相应的推力器样机[5-8]。
不同发射模式下的场发射电推力器的工作参数相差甚远,例如离子液体电推力器的工作电压可低于2 kV[9],而FEEP推力器的工作电压可能达到上万伏[4]。在此基础上,不同类型推力器的推力参数也大为不同,其发射电流/推力/比冲等可在较大范围内变化。针对不同的空间任务推力需求,需要场发射电推力器实现不同的推力效果。因此需要明确场发射电推力器的发射机理,明确不同模式的产生条件,并对不同模式下场发射电推力器的推力参数调控方法进行分析。
本文首先阐述了不同模式下场发射电推力器发射过程的基础物理机制,以此为基础讨论了多种形式的推力器参数选型与应用方向。从对发射过程的物理机制的讨论发现,由于离子液体电推力器在工作参数的调控下,可以工作在多种发射模式下,从而可以实现工作参数的大范围调节。对此设想,我们进行了初步的试验验证,通过试验研究了一种离子液体电推力器的发射过程,对发射过程的液面形貌和发射电流进行了采集,并对推力性能进行了计算分析。试验结果表明,通过改变外加电压可以改变推力器的发射模式,进而实现对推力参数的调控。本文的结论可为未来的推力器结构及性能设计提供参考。
1 场发射电推力器的基础物理过程
1.1 场发射原理
场发射电推进技术是静电推进技术的一种,其基本原理为在外加电场的作用下,从导电液体表面静电抽取出带电粒子,带电粒子在电场中加速飞出从而产生推力。典型的场发射电推力器由发射极、抽取极、电源和推进剂供给系统等组成,如图1所示。随着外加参数的不同,推力器会产生不同荷质比的带电液滴或带电离子。
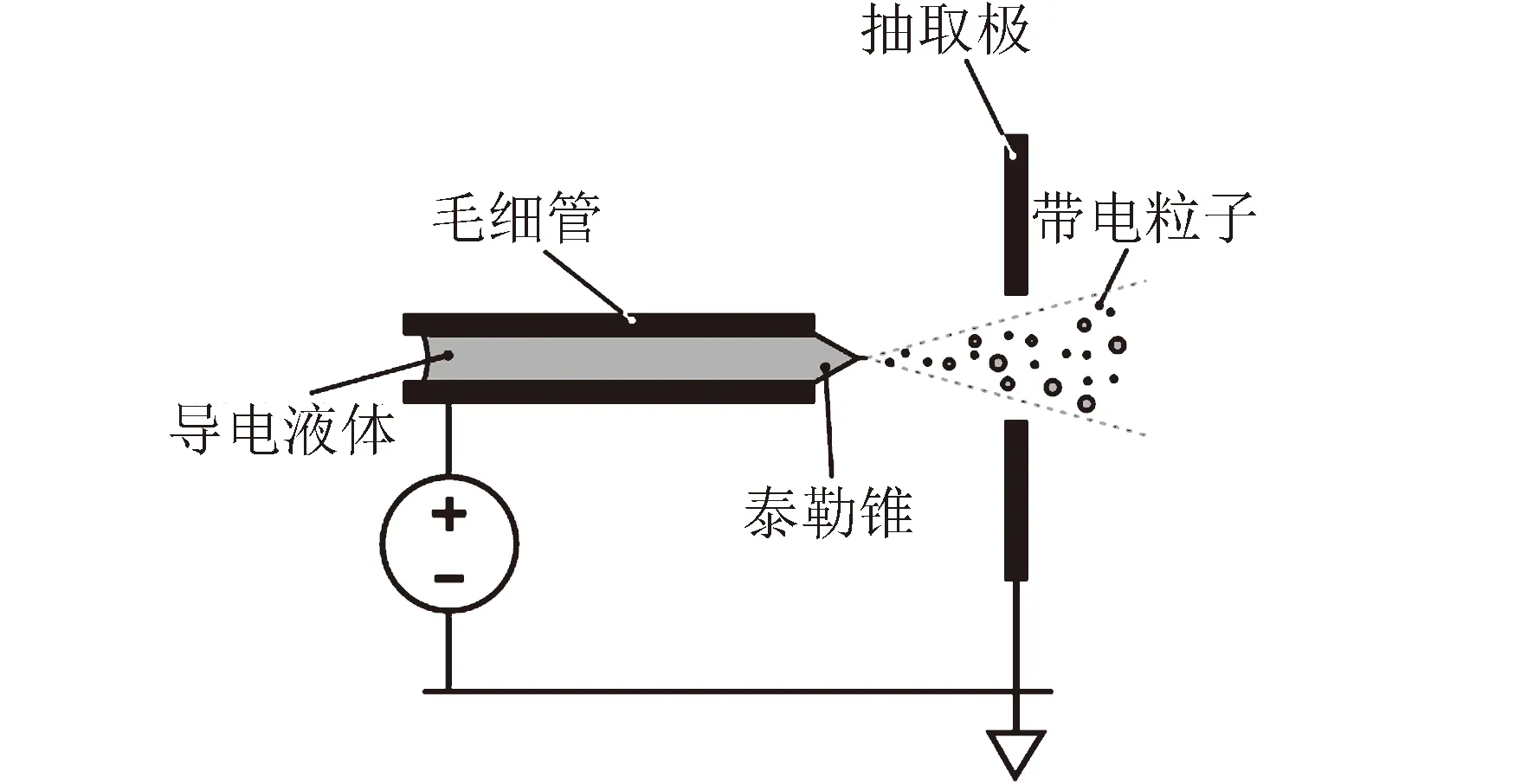
图1 场发射电推力器原理示意Fig.1 Operation principle of field emission electric thrusters
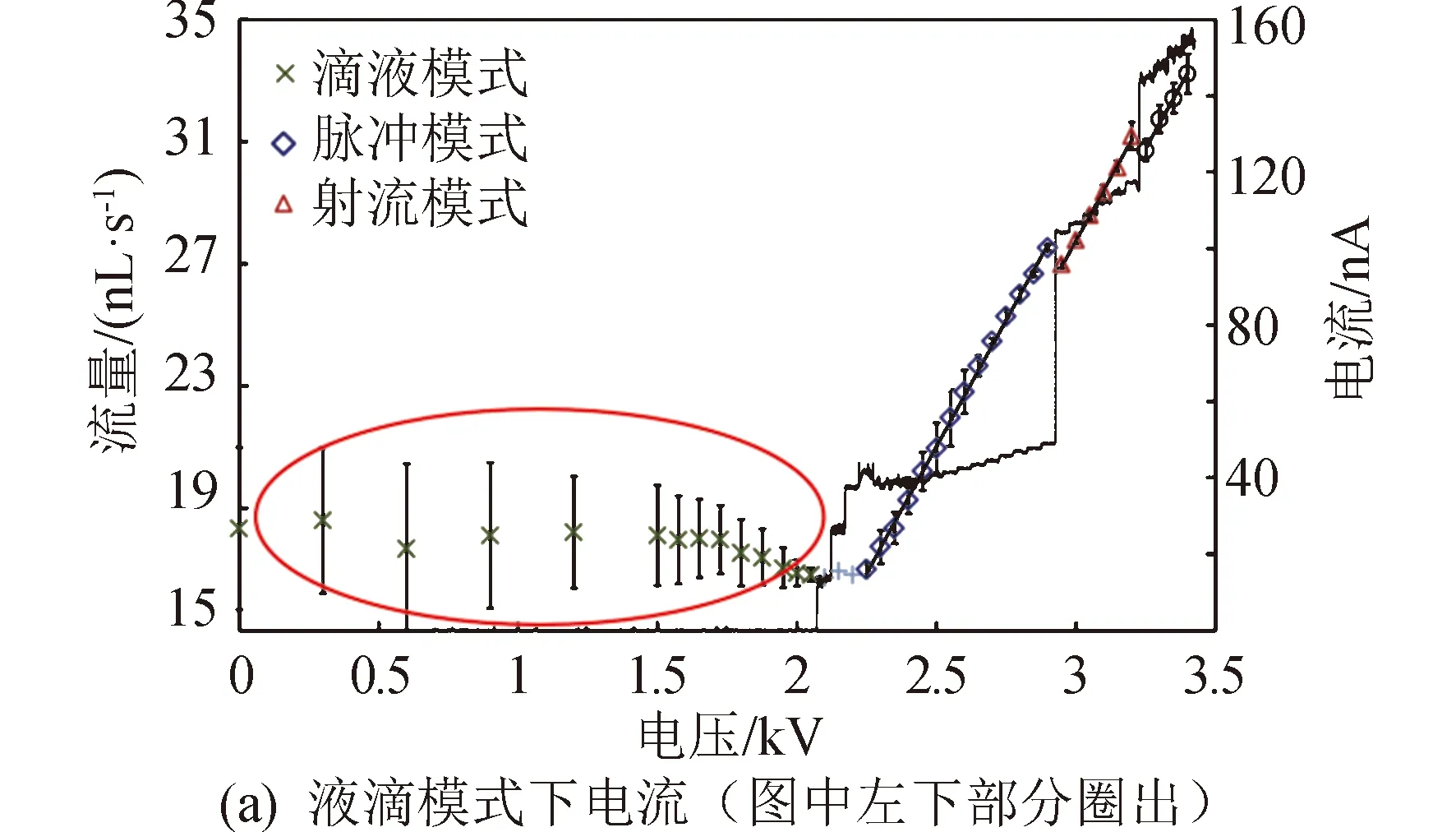
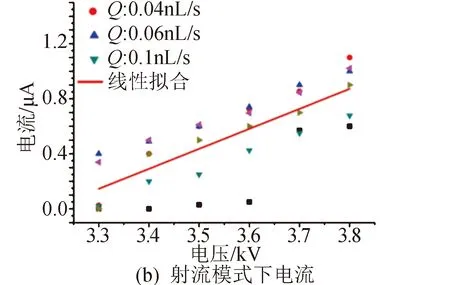

图2 不同发射模式电流曲线[10]Fig.2 Current curves in different emission modes [10]
图2所示为文献[10]研究的推力器发射模式随电压的变化关系。在场发射电推力器的发射过程中,存在液滴模式、射流模式和离子模式几种不同的发射模式。以往的文章中对不同发射模式下的场发射推力器发射过程进行了广泛的研究。可以看出在较低电压条件下,即图2(a)中左下角圈出的部分首先会出现液滴发射模式,在此模式下的发射电流值相对较低,且产生的带电液滴尺寸与发射极孔径在同一量级。液滴模式下的发射状态如图3(a)所示[11]。随电压的增大,发射模式会逐步变为射流模式,射流模式下形成的电流较液滴模式有明显提升,且此模式下的电流与电压有较好的线性相关性,如图2(a)(b)所示。在射流模式下的液面会形成泰勒锥结构,并在锥尖处形成细的射流,射流末端由于射流破碎形成带电的液滴群,此时形成的带电粒子尺寸显著降低,如图3(b)所示。随着电压的继续增大,当液面处电场强度足够大时,会出现离子发射模式,在离子模式下能得到电流随电压的指数相关性,如图2(c)所示[12]。


图3 不同发射模式图像[11]Fig.3 Emission images of the thrusters[11]
在实际的推力器工作过程中,通过在发射极与抽取极之间加载高电压,可以使得发射极出口处的液面具有一定的电场强度,当电压足够高,使得液面处电场强度值足够大时,即会将液面拉伸成泰勒锥,进而形成发射。Lozano给出了在场发射电推力器的电场构型下,开始产生发射所需的起始电压计算公式如下[13]:
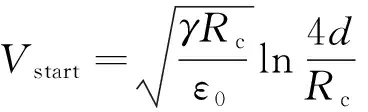
(1)
式中:γ为表面张力系数;Rc为毛细管内径;ε0为真空介电常数;d为针-板间距。由式(1)可以看出,起始电压的数值的影响参数包括推进剂物性以及推力器的几何构型。
1.2 发射的不同机制
(1)液滴模式
在场发射电推力器的工作过程中,在外加电压值较低的情况下,会出现液滴发射模式,在此模式下发射的带电粒子为大尺寸的带电液滴,液滴尺寸与发射极孔径相当。由于体积较大,其粒子的荷质比较相应较低,文献中指出一种液滴模式的典型工况下,带电粒子荷质比为10-8C/g量级[14],与之相对的,典型的射流模式下粒子荷质比在1 C/g以上,而离子模式下的带电粒子荷质比可达到100 C/g量级[15]。由于液滴发射模式下过于微小的带电粒子荷质比,此模式难以在空间推进中得到使用。
(2)射流模式
当作用在液体表面的电场强度足够大时,液面在表面张力和电场力的共同作用下会形成稳定的锥形结构,即泰勒锥[16],如图4所示。
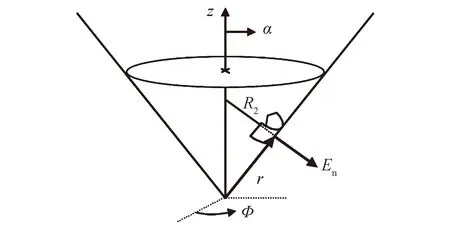
图4 内角为α的泰勒锥的几何模型Fig.4 Geometry of a Taylor cone with inner angle α
泰勒的模型是建立在表面张力和电场力平衡之上,即:
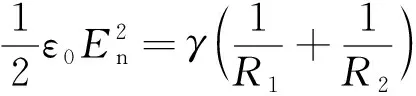
(2)
式中:En为电场强度;R1和R2为液体表面特定点的曲率半径。对于设定内半角的锥结构,R1是无穷大,R2=rtanα,r为锥表面一点距锥尖的距离。由式(2)可得到法向电场力的表达式:
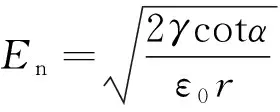
(3)
式中:α为泰勒锥半角。从式(3)可看出,在逐渐靠近锥尖的过程中,液体表面的电场强度会不断增大。当电场强度足够大时,电场力将克服表面张力的作用,将锥尖变形成一个细的射流,射流在电场作用下以高速远离锥结构。在射流的末端,由于流动的不稳定性等原因,射流将破碎成带电的液滴或离子,这被称为场发射电推力器的射流模式。
射流模式的产生是液体流动与外电场作用的耦合过程。文献[17]中指出,在射流形成处液体的流动弛豫时间与电荷弛豫时间相当,这可用公式可表示为:
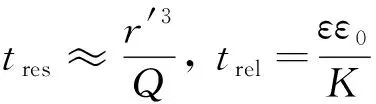
(4)
式中:tres为流动弛豫时间;trel为电荷弛豫时间;Q为流量;r′为锥尖处曲率半径;K为电导率。整理式(4),可得出一个特征长度为:
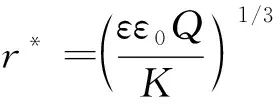
(5)
式中:r*为电荷弛豫长度。通过电荷弛豫长度可进而得到射流半径的计算公式为:
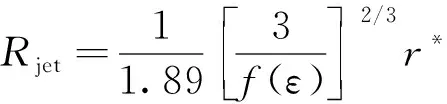
(6)
式中:Rjet为锥射流特征尺度;f(ε)为液体参数,由静电常数决定。通过式(6)可以计算得到射流的特征尺寸参数。将射流半径代入式(3)中,还可以计算出形成射流所需的电场强度值。此外,通过大量试验得到了射流模式下的电流和式(7)很好的关联性。此电流计算式能够准确预测液滴射流模式下的场发射电流值[17]:
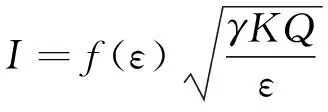
(7)
(3) 离子模式
从式(3)可看出,法向电场随靠近锥尖而逐步增大。最终,若电场足够大,会直接从液体表面抽取出离子,这个过程被称为场蒸发。场蒸发的发射条件和量化参数最早由Iribarne等提出[18]。场蒸发电流密度计算公式如下:
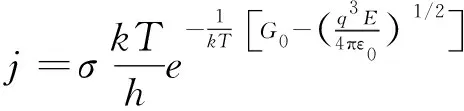
(8)
式中:j为离子电流密度;σ为液体表面电荷密度;k为玻尔兹曼常数;T为系统温度;h为普朗克常数;G0为蒸发自由能;E为外电场。由式(8)可知在场发射电推力器中,场蒸发的产生由外加电场强度控制,当电场强度足够克服液体蒸发自由能时,即可产生离子的场蒸发现象。由式(8)可得到产生大量离子发射所需满足的电场强度条件为:
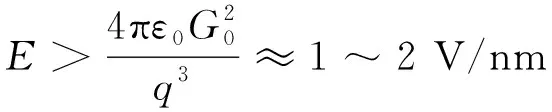
(9)
2 发射模式及推力参数的调控方法
2.1 发射模式的调控
在第1.2小节中阐述了场发射电推力器工作过程中可能出现的几种不同发射模式以及各自的物理机制。由于外加电场的作用,发射极出口处的液面在电场力作用下拉伸突起,最终形成泰勒锥。随着靠近锥尖,液面处的电场强度值会不断增大,若电场强度满足式(9)所示的条件,就会由场蒸发从液面上抽取出带电离子,形成离子发射;在推进剂物性和供给流量确定的条件下,射流的特征尺寸可通过式(6)进行计算,进而可以由式(3)计算得到产生射流所需满足的电场强度条件。即通过对发射极液面尖端处电场强度的计算,可以对推力器所处的发射模式进行判断。
图5(a)、图6(a)、图7(a)为分别使用液态铟/甲酰胺/离子液体EMI-BF4作为推进剂计算得到的不同流量条件下射流产生所需场强和离子蒸发所需场强的量化关系。由于在确定的推进剂下,场蒸发产生所需满足的电场强度值为定值,不随流量而变化,如图中红线所示;而射流产生所需场强如图中绿线所示。而图5(b)、图6(b)、图7(b)为不同流量下离子发射产生的电流值和射流产生的电流值的量化关系。图中绿线所示为射流产生的电流;红线所示为离子发射产生的电流。计算中采用的流量范围为0.01~10 nL/s,采用的推进剂物性参数如表1所示。
对图5分析可看出,在液态铟作为推进剂的情况下,不同流量时的场蒸发所需场强均远低于射流所需场强,因此更易产生离子发射,反映在电流组成上即为离子电流占据主导,即推力器工作在离子模式;类似地,从图6可看出在以甲酰胺作为推进剂的情况下,不同流量时的射流所需场强均远低于场蒸发所需场强,因此更易产生射流发射,反映在电流组成上即为射流电流占据主导,即推力器工作在射流模式。
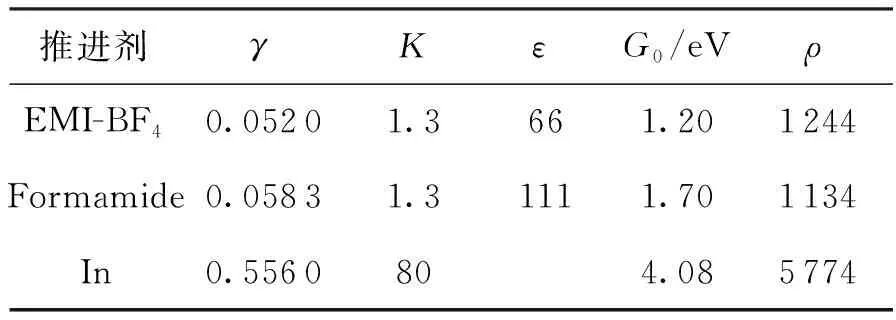
表1 推进剂物性参数
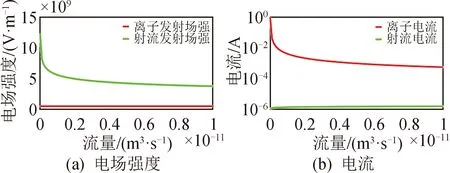
图5 液态铟不同模式下场强/电流对比Fig.5 Electric field and current in different mode of liquid In
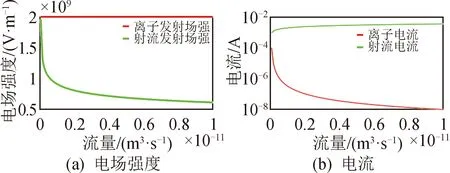
图6 甲酰胺不同模式下场强/电流对比Fig.6 Electric field and current in different mode of formamide
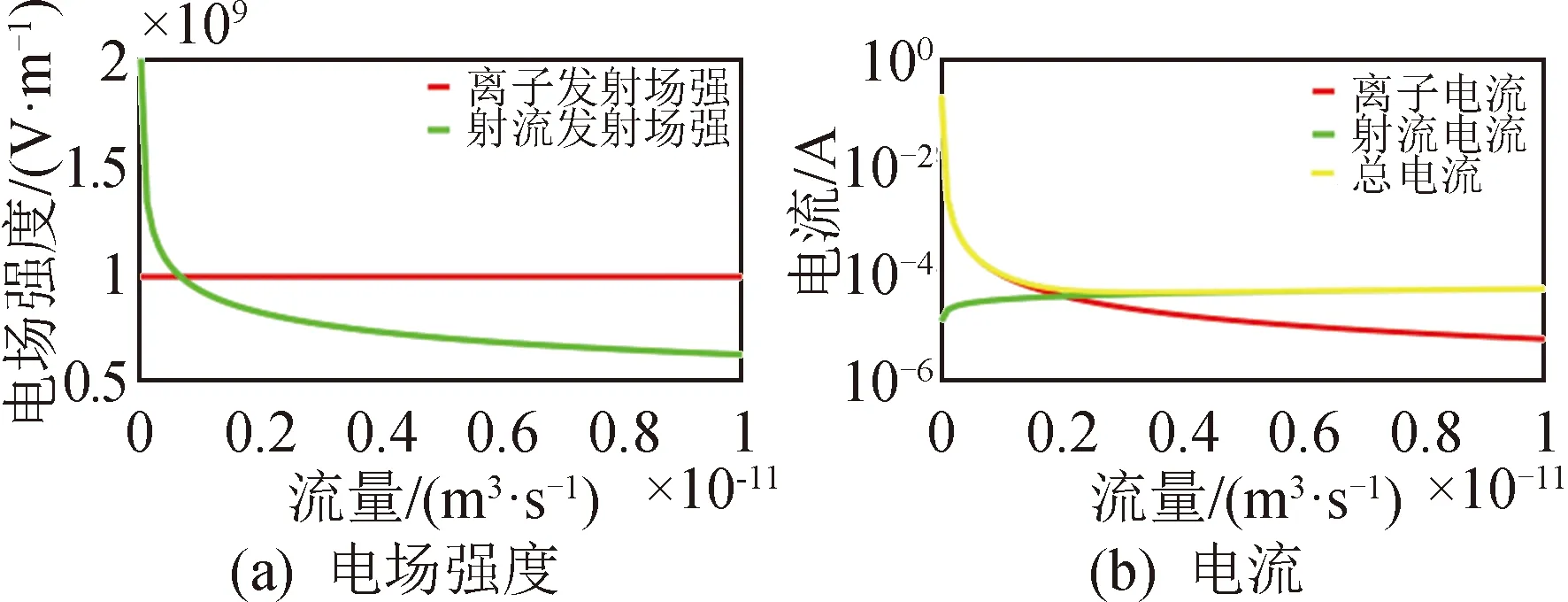
图7 EMI-BF4不同模式下场强/电流对比Fig.7 Electric field and current in different mode of EMI-BF4
而图7的结果说明,采用离子液体EMI-BF4作为推进剂时,推力器可以工作在不同的模式下。由图7(a)可看出,以离子液体EMI-BF4作为推进剂时,在低流量条件下场蒸发场强低于射流场强,因此更易产生离子发射;而在较高流量条件下场蒸发场强高于射流场强,因此更易产生射流发射。由第2.2小节的结果可推导出离子电流密度随流量的减小而增大;而射流电流随流量减小而减小的结论,如图7(b)所示。当流量非常小时,电流由离子电流占主导,推力器工作在离子模式,而随着流量的增大,离子电流逐渐减小,同时射流电流逐渐增大,在图7(b)中流量为0.2 nL/s附近,可以看到射流电流与离子电流相当的情况,可认为此时处于混合发射模式;而随着流量进一步增大,离子电流快速降低,逐渐进入射流模式。
通过以上分析计算可看出,通过改变场发射电推力器中所使用的推进剂种类,可以对发射模式进行调控,其中离子液体EMI-BF4可以工作在多种发射模式下,具有更大的调控范围。
2.2 推力参数的选择与调控
在场发射电推力器中,推力和比冲的计算可以由能量守恒方程得到。场发射产生的带电粒子会在电场中加速飞出,从而产生推力。最终,输入推力器的电能几乎全部转化为带电粒子的动能,则带电粒子在电场中最终达到的速度为:
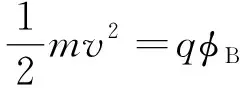
(10)
式中:m为带电粒子质量;v为带电粒子速度;q为粒子带电量;φB为束流电压。整理式(10)可以得到粒子在电场中加速后最终获得的速度为:
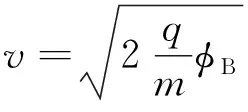
(11)
进而可以得到场发射电推力器的推力和比冲的计算公式为:

(12)
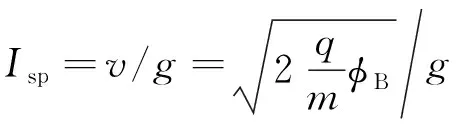
(13)
从式(12)(13)可以看出,场发射电推力器的推力性能受到抽取出带电粒子的荷质比q/m的影响,此外还受到外加电压/供给流量等参数的控制。由第2.1小节的内容可知,在实际的推力器工作过程中,根据所使用推进剂的种类的不同,会使得推力器工作在不同的发射模式。当采用胶体作为推进剂时,推力器工作在射流模式,产生的为荷质比低的带电液滴,因此推力器产生的比冲较低,但可达到更高的推力;而采用液态金属作为推进剂时,推力器工作在离子模式,产生的为荷质比高的带电金属离子,可达到更高的比冲,而推力则会相对下降;对于离子液体电推力器而言,由于在工作参数的调控下,推力器可以处于多种发射模式,推力器既可产生荷质比高的带电离子,也可以产生荷质比高的带电液滴,因此可以实现推力参数的大范围调节。
3 试验研究及结果分析
由于发射模式的不同,场发射电推力器的推力性能可以产生显著的差异。特别是对于离子液体电推力器而言,在适当的推力器结构下,仅仅调节工作电压或流量,就可以使得推力器工作在不同的发射模式,进而可以大范围的调节推力器性能。因此我们设计了相应的原理实验,对离子液体电推力器的推力性能调节方法进行验证。为此设计了一种主动流量供给型的场发射电推力器,采用离子液体EMI-BF4作为推进剂,通过改变外加电压/流量/极板间距,进行了大气下发射试验,对不同情况下的发射电流进行采集,并通过计算得出相应的推力和比冲。
3.1 试验系统
试验系统由离子液体电推力器、高压及交变电源、电流采集系统、推进剂供给系统、显微摄像系统组成,如图8所示。工作电源为一台直流高压电源,电源具有正负两路输出,可实现0~±10 000 V的电压调控。高压电源输出的高压由一台电源交替开关控制,电源交替开关将直流高压电源的正偏压和负偏压信号以1 Hz的频率交替输出。采用抽取极接高压,发射极接地的电路连接方式,发射电流通过电流放大器进行采集,采集到的电流信号可经示波器输出显示电流波形并计算平均电流值。离子液体EMI-BF4通过注射泵进行供给。为了对试验中的场发射现象有更直观的认识,采用一台CCD相机及相应的远心镜头对发射极尖端的液面形貌进行实时观测。离子液体电推力器采用单个的石英材质毛细管作为发射极,发射极内径0.3 mm,外径0.5 mm。抽取极为一个直径40 mm的不锈钢圆板,中间开有1 mm的孔。发射极-抽取极之间的距离可以通过与抽取极相连的位移滑台进行调整,调整精度为1 mm。
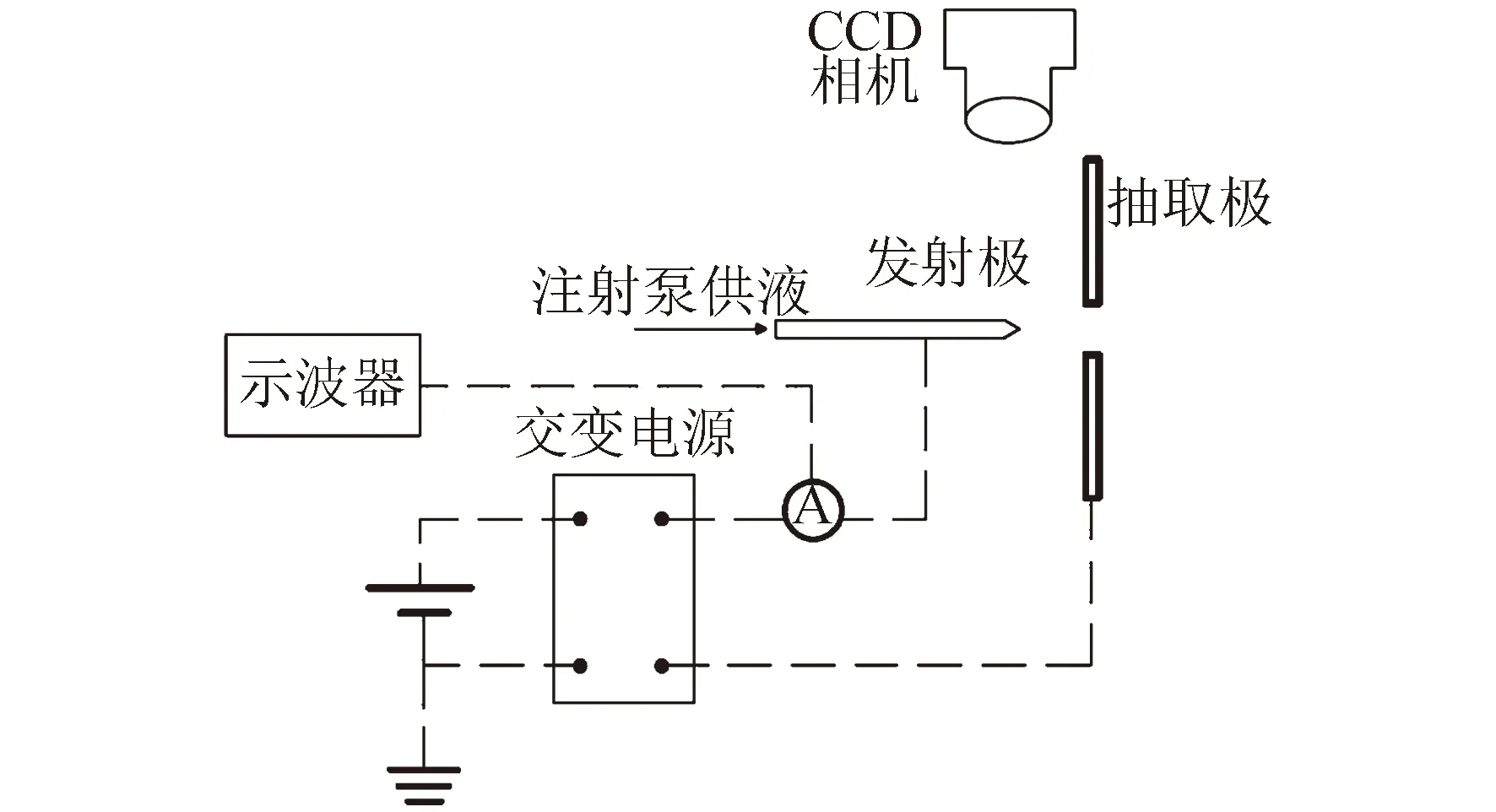
图8 离子液体电推力器实验系统原理Fig.8 Schematic of ionic liquid thruster experimental setup
3.2 结果与讨论
3.2.1 大气下场发射试验
(1)发射模式随电压的变化
在大气环境下,通过改变外加电压值,对不同电压时发射过程的电流信号进行采集,得到了如图9所示的不同电压下发射电流波形曲线。通过图9(a)(b)(c)的结果可看出,在较低电压(3 160~3 580 V)时,推力器处于液滴发射模式,采集到的电流波形呈现周期性发射现象,并且发射频率随电压的增大而增大。图9(a)中的发射频率约为100 Hz,而到图9(c)时发射频率则增大为约400 Hz。频率随电压的正相关性与文献[12]中的现象一致。随着电压的继续增大,发射模式由液滴模式转变为射流模式,电流波形也由之前的周期性发射变为图9(d)所示的稳态波形。
(2)外加电压对发射电流的影响
通过对不同电压下采集到的电流曲线进行分析计算,得到发射电流随外加电压的变化规律如图10所示。试验中发射极与抽取极间距为4 mm,供给流量为6 μL/h。分别采用抽取极接正高压和负高压的加电方式进行相应试验,推力器分别产生负电荷和正电荷,得到如图10所示的两种模式下推力器的电压-电流曲线。从图10可以看出,不同的发射模式下,开始采集到电流时的起始电压值都在3 000 V上下,高于此起始电压时,发射电流随电压的增大而增大。此外,相同电压值下,当液面处分别聚集正极性和负极性的带电粒子时,液面的状态不同,这导致了发射电流值的不同,发射负粒子情况下的电流值大于正粒子情况下的电流值。在试验中改变发射极-抽取极间距,研究了不同间距下的电压-电流关系,供给流量为3 μL/h,结果如图11所示。从图11中可以看出,在不同间距下,推力器发射电流值均随电压增大而增大。而在相同电压值下,发射电流随间距的增大而减小。
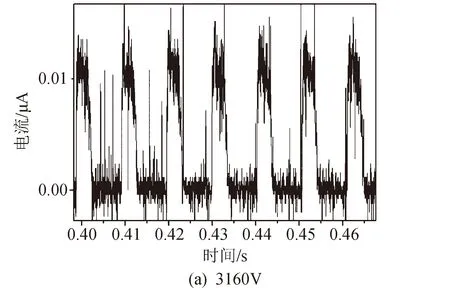
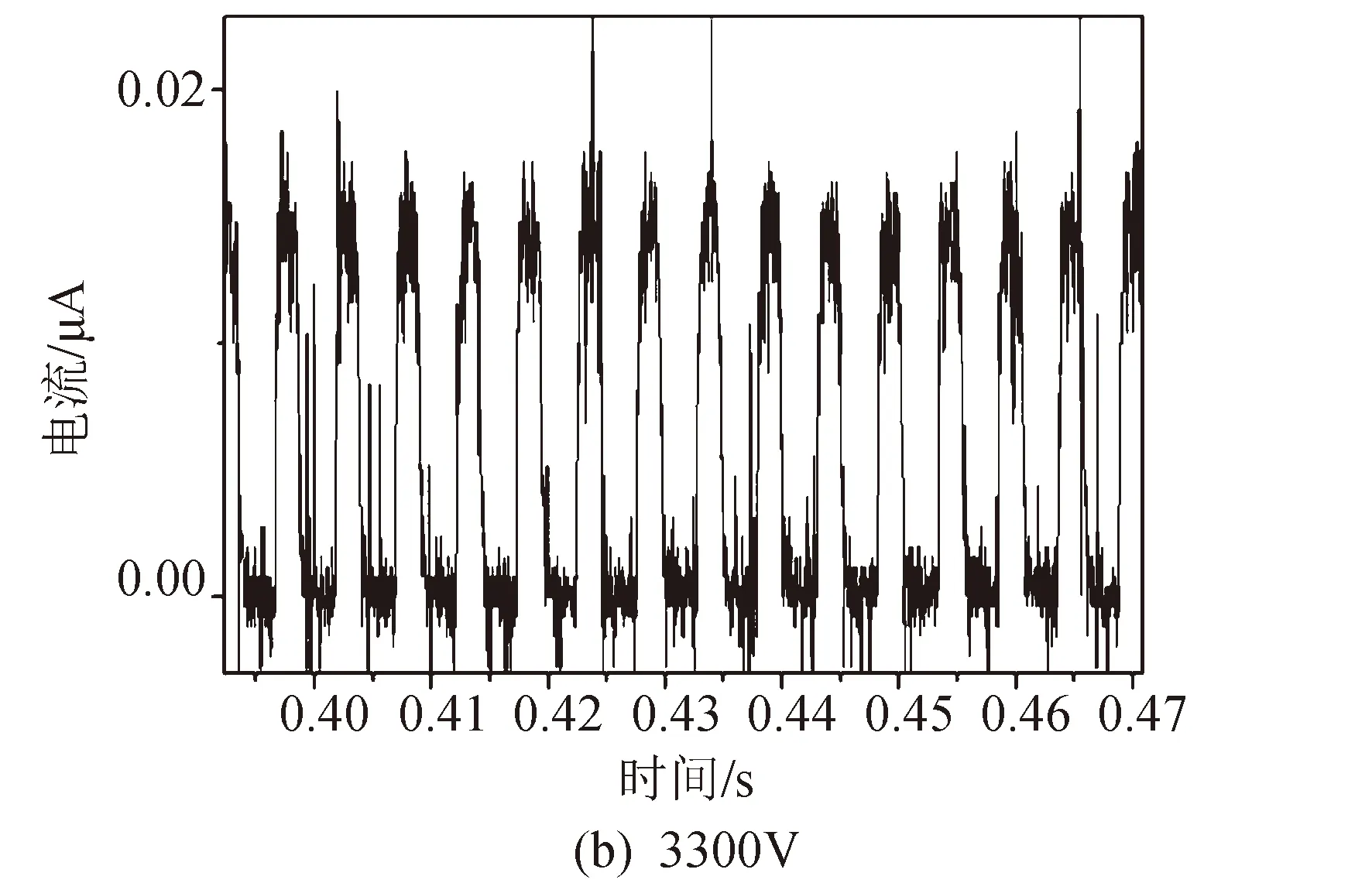
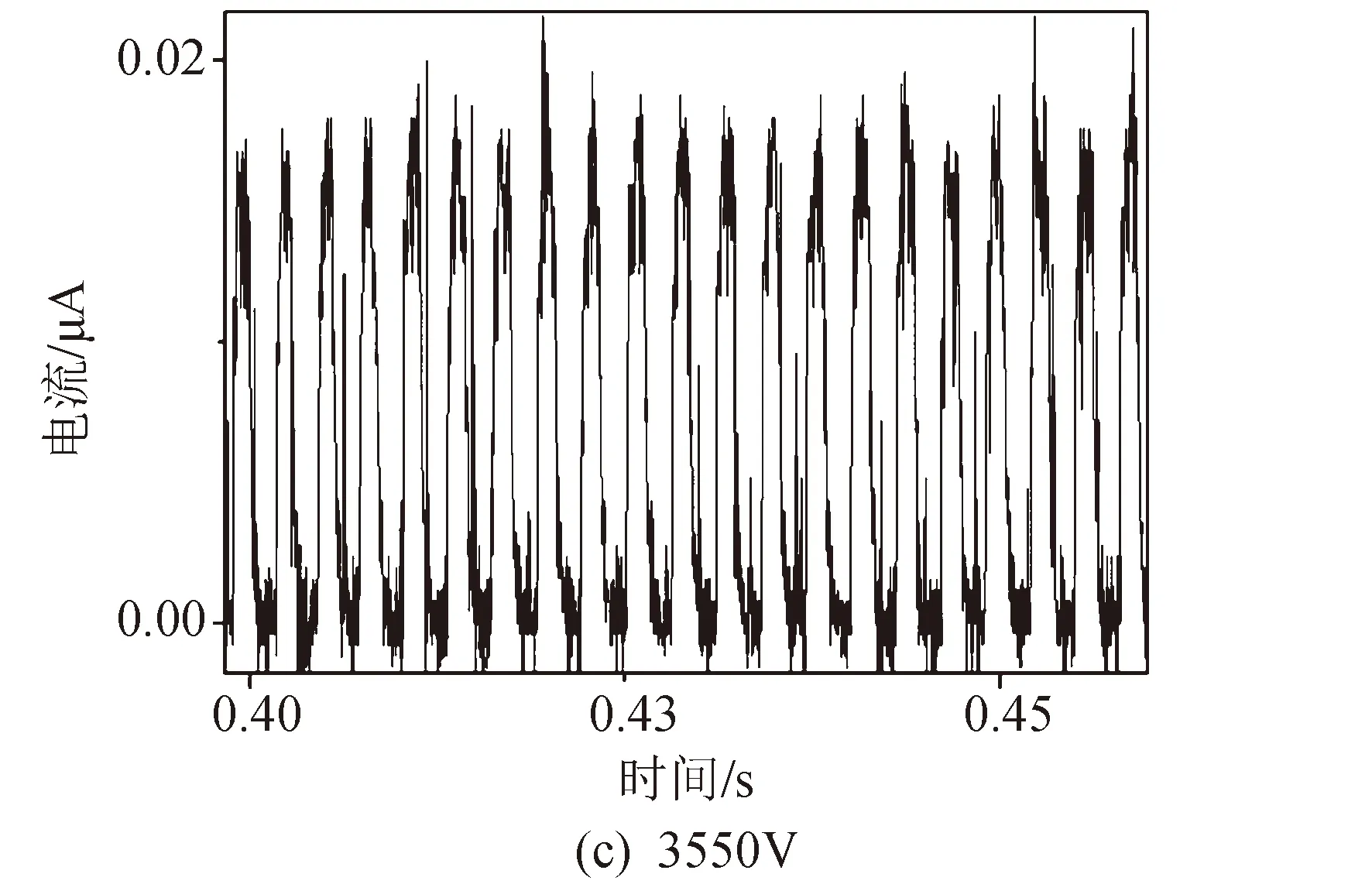
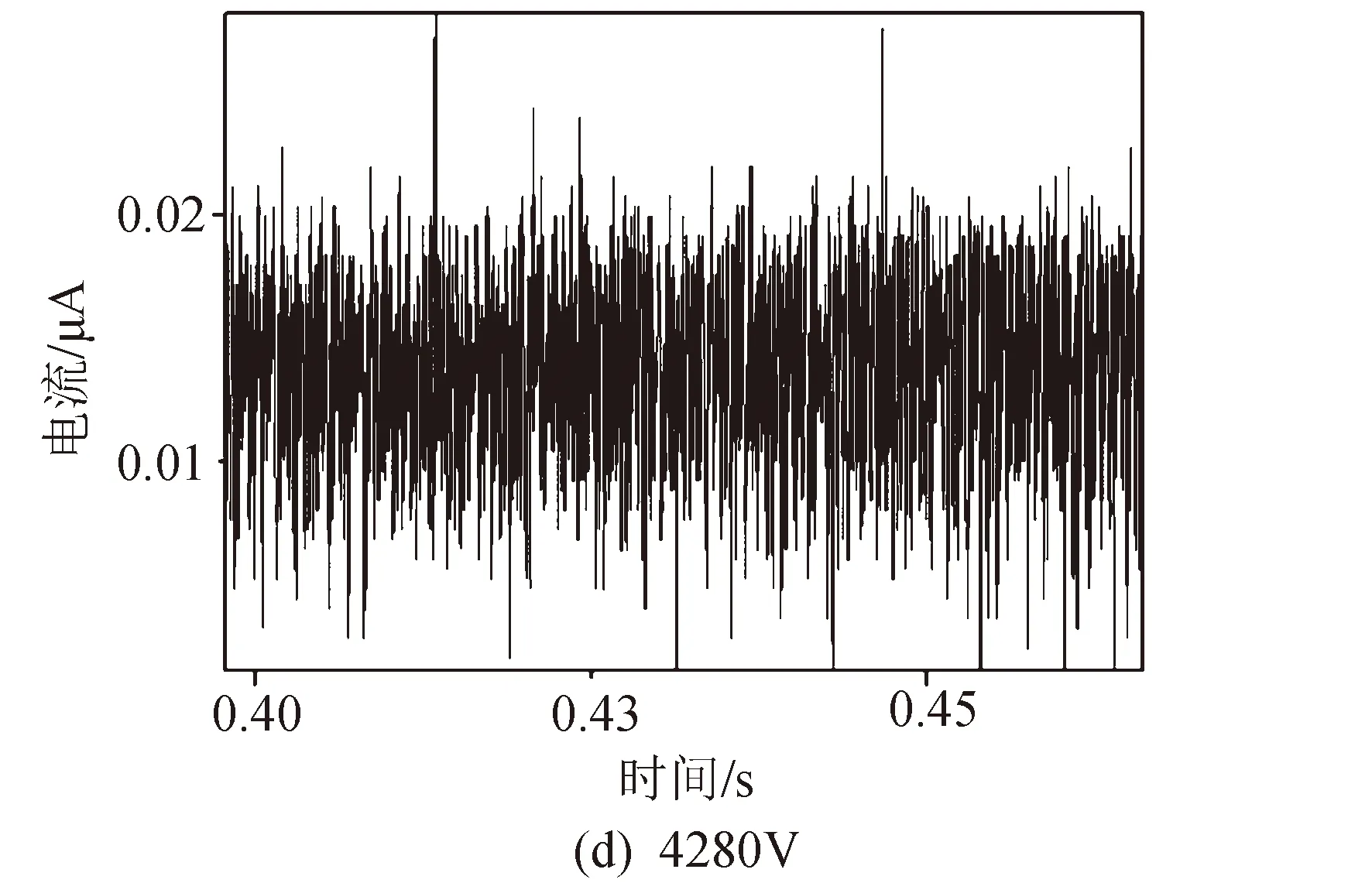
图9 不同电压下的发射电流曲线Fig.9 Current curves in different applied voltages
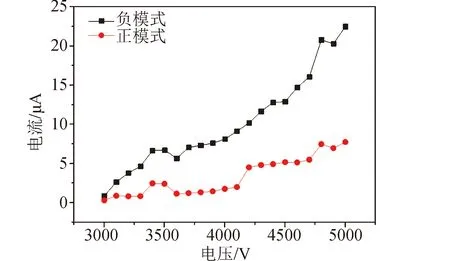
图10 发射电流随外加电压的变化过程Fig.10 I-V curves of the emission process
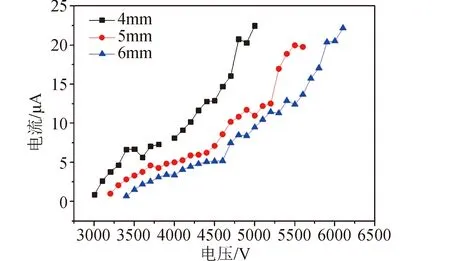
图11 不同针板间距下的电流-电压曲线Fig.11 I-V curves in differentemitter-extractor distances
(3)大气下发射电流的组成
通过分析图10的大气发射电流发现,此发射电流中除场发射电流之外,还包括大气电晕放电的电流。这是由于在大气环境下存在大气电晕放电现象,而在此推力器尺寸下,大气电晕放电产生所需达到的电场强度值低于离子液体EMI-BF4产生场发射现象的电场强度值,因此在测量到的电流值中,大气电晕放电电流占据了一定比例[19]。通过以上分析可知当前大气下得到的电流组成为场发射电流和大气电晕放电所产生的电流。除了影响电流组成,大气电晕放电的形成会改变液面处电场构型,进而改变液面形状,图12为在发射过程中实时采集的大气下发射极液面形貌。从液面形貌可看出液体在电场力作用下拉伸成锥状,并形成发射,但液面形貌与锥射流仍有区别。为了去除大气电晕放电现象对发射过程的影响,将推力器放入真空舱内进行了相应的真空发射试验。

图12 发射极出口处液面的泰勒锥形貌Fig.12 Taylor cone structure at the end of the emitter
3.2.2 真空下场发射试验
在大气试验之后,将离子液体电推力器放入真空舱内进行了真空下试验,用于与大气试验进行对比。真空试验中采用的发射极为电喷针,其外径为360 μm,内径50 μm,针尖处内径逐渐收缩至30 μm。以此作为推力器结构,在流量为6 μL/h下采集得到的真空下场发射电流数据如图13所示。图13还给出了相同参数下的大气发射电流结果。由图13的结果可以看出,相同工况下的真空发射电流数值远高于大气电流数值,且通过真空电流曲线可看出与离子发射电流公式所描述的电流随电压的指数变化关系有较好的吻合,因而认为在真空条件下达到了离子发射模式。而相同工况下的大气电流较小,则是由于大气放电的产生使得液体表面场强下降,使得液面处的电场强度值在大气下无法达到场蒸发所需的数值。而真空下由于没有大气放电现象,因而随着电压的不断增大液面处可以达到很高的电场强度,由场蒸发现象产生了大量离子发射,进而产生了如图13所示的高电流值。
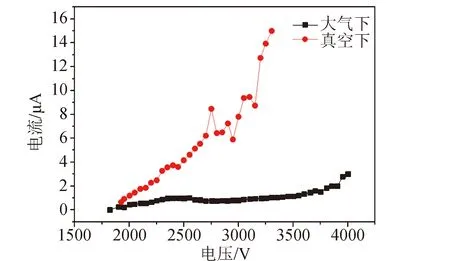
图13 真空下与大气下发射电流对比Fig.13 Currents in vacuum and atmosphere environment
3.2.3 推力参数
以第3.2.2小节中的真空下试验结果,通过式(12)(13)可以分别计算得出不同电压下推力器产生的推力及比冲值。结果如图14所示,可看出,随着电压的增大,推力器的推力和比冲都不断增大,实现了通过改变电压对推力参数进行调控的目的。其中推力范围为1.6~10 μN,比冲范围为154~978 s。
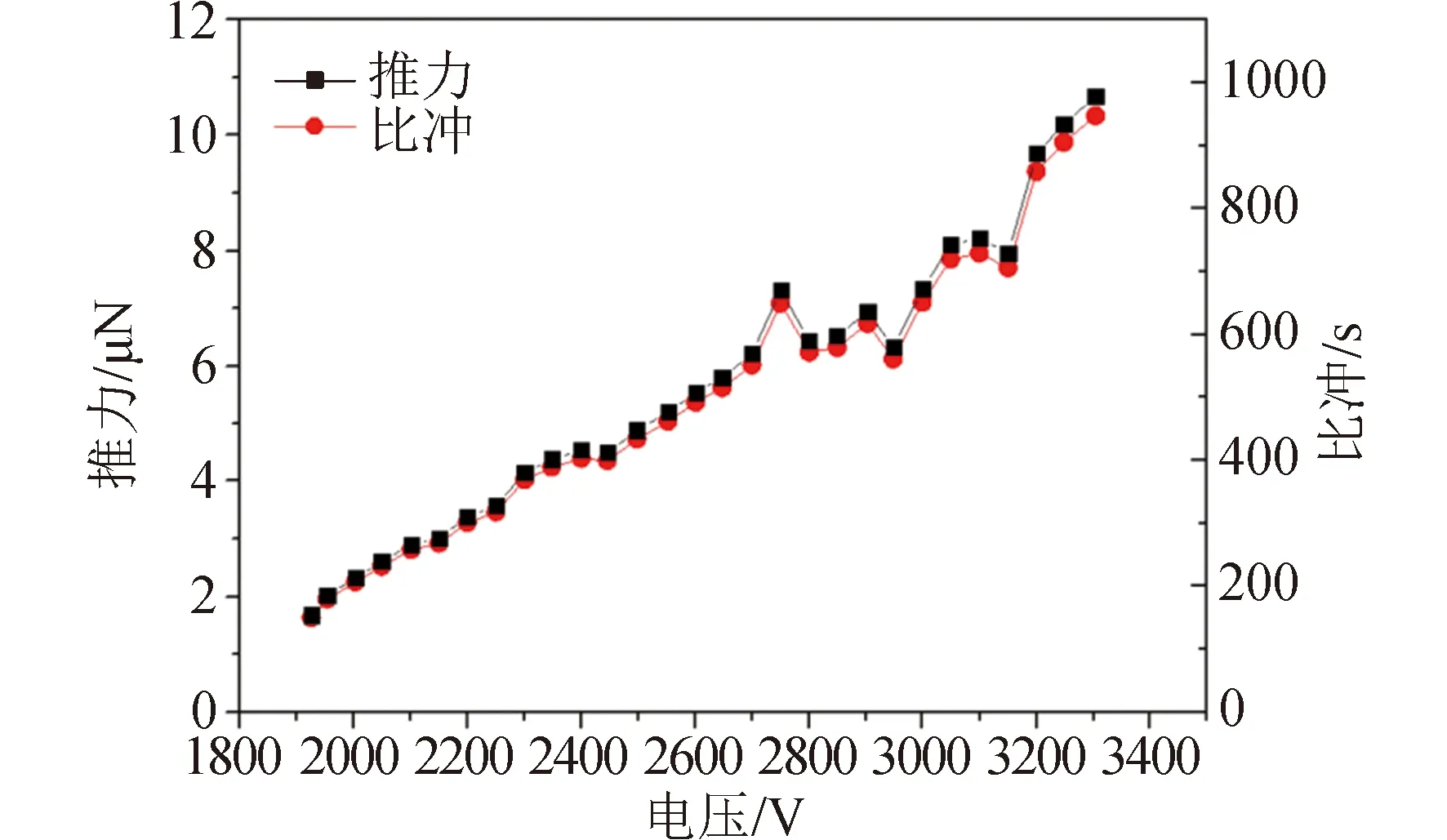
图14 真空实验下计算得到的推力和比冲Fig.14 Calculated thrust and specific impluse based on the experimental results in vacuum
4 结束语
本文以场发射电推力器推力性能的调控作为出发点,对场发射电推力器发射过程中的基础物理机制进行了分析,对推力性能的影响因素和其调控方法进行了说明,在此基础上进行了相应的实验研究,得到的结论如下:
1)场发射电推力器的发射过程是电场力与液体表面张力共同作用的结果,存在液滴模式、射流模式和离子模式等不同发射模式。且决定每种发射模式的物理基础不尽相同,导致在不同的推进剂种类、推力器参数中,场发射电推力器存在不同的发射状态。
2)本文针对场发射电推力器的推力参数的选择与调控方法,从理论分析和试验研究两方面入手,对决定推力性能的推力器发射模式及其物理基础做出了解释。场发射电推力器的推力性能主要由推力器所处的发射模式决定,由于不同发射模式下产生的带电粒子荷质比不同,会导致推力器的推力参数范围产生明显不同。场发射电推力器的发射过程受到推进剂种类/供给流量/外加电压/推力器结构等多种因素的影响,可以产生不同的推力效果。
3)本文中设计了一种主动供给型离子液体电推力器进行试验,实现了推力器在大气和真空条件下的不同发射模式。通过对真空下发射电流等数据的采集和计算,得到相应的推力/比冲值,结果表明,本试验实现了通过改变外加电压的方法对推力参数进行调控,推力器达到的推力范围为1.6 ~10 μN;比冲范围为154~978 s,此结果可为后续的场发射电推力器设计提供参考。

