脉冲等离子体推力器电磁加速机理数值研究
杨三祥,刘超,王尚民,冯杰,陈娟娟,吴辰宸,贾艳辉,郭宁,耿海
兰州空间技术物理研究所 真空技术与物理重点实验室,兰州 730000
随着微电子技术和微加工技术的发展和成熟,具有质量轻、体积小、发射和运行成本低、研制周期短等特点的微小卫星研究和应用日渐升温。卫星要实现小型化和轻量化,其分系统就必须具备小型化和轻量化的特点。由于受限于整星的重量和功耗,应用于微小卫星的电推力器只能选择低功耗、小质量的微推力器。脉冲等离子体推力器(pulsed plasma thruster,PPT)是一种将含能固体工质烧蚀、电离所产生的等离子体在洛伦兹力作用下加速喷出而产生推力的电磁型微推力器,它具有比冲高、功耗低、体积小、结构简单等优点,可满足微小卫星的空间动力应用需求,尤其适合执行对控制精度要求高的任务。
为了提高PPT的效率,国内外开展了大量关于PPT的理论和试验研究。1996年Spanjers等[1]用高速相机、干涉仪等设备研究了PPT放电之后放电通道中的中性气体和大颗粒的形成,结果表明形成大颗粒的主要原因是工质表面喷射的熔融特氟龙或积碳所致。1998年Spanjers等[2-4]利用扫描电镜和高速照相机等设备测定了PPT喷射的直径在1~100 μm大颗粒的质量和速度,结果表明PPT喷射的大颗粒约占每次烧蚀质量的40%,而对推力的贡献却不到1%。Koizumi等[5]应用发射光谱、高速摄影、磁场探针等诊断手段研究了平行极板PPT中工质的电离加速,结果表明二次放电发生在与工质表面有一定距离的中性气体团的外侧,其对工质的加速作用很小。Nawaz等[6]利用磁场探针测量了PPT放电通道中不同位置处的磁场,结果发现在工质表面附近测量的磁场与弹丸模型计算所得的磁场复合较好。Pottinger等[7]采用弹丸模型开展了数值研究,认为电极间的电感梯度是决定推力器性能的关键因素,电感梯度越大,离子获得的动能越大。Schönherr等[8]对具有扩张角的尖嘴极板推力器进行了试验与仿真研究,计算得到的推力器效率与Pottinger等[7]的结论基本一致。国内目前主要有国防科学技术大学、中国科学技术大学、兰州空间技术物理研究所等科研院所开展PPT样机的研制和机理研究,并取得了许多有意义的结果[9-12]。
脉冲等离子体推力器的研究虽然在试验和理论上都取得了许多结果,但是还存在以下几方面的问题:1)电流片模型得到的结果只在工质表面附近,与试验结果符合,在其他位置二者结果相差较远[6];2)Schönherr等关于推力的结果是通过电流波形推导得到的,其结论的合理性还有待进一步确认[8];3)对脉冲等离子体推力器在工作过程中积碳形成的机理研究还不够完善,需要进一步研究。因此,为了加深对脉冲等离子体推力器工作机理的理解和提高脉冲等离子体推力器的性能,对脉冲等离子体推力器的理论和试验研究还需深入。
本文利用一维集成电路模型,系统地分析了推力器初始放电电压和电极间距对推力器推力、比冲、等离子体密度和电子温度分布的影响。本文的研究旨在加深对PPT电磁加速机理的理解,为后续PPT性能的优化和产品的小型化提供理论支撑。
1 方法
1.1 PPT电磁加速模型
PPT推力器中等离子体的加速过程可以分为两个阶段:电热加速阶段和电磁加速阶段。电热加速发生在推进剂表面,即放电发生区域。等离子体一旦形成,电容、电极、等离子体之间将形成放电回路。由于等离子体电阻的存在,放电产生大量热量烧蚀推进剂表面,使得推进剂表面的压力急剧升高,产生的粒子被气动力加速。此时,电弧烧蚀工质表面电离产生的等离子体密度低,电流小,离子所受的洛伦兹力相对较小,电磁加速作用微弱,加速由热能主导。随着等离子体向喷口处运动,一方面,由于腔体的体积变大,压力减小,电热加速作用逐渐减弱;另一方面,由于放电电流的增加,电磁加速作用逐渐增强。当带电粒子离推进剂表面一定距离时,电磁加速贡献大于电热加速的贡献,电磁加速开始起主导作用。本文基于Shaw等开发的集成电路模型[13-14],研究了PPT电磁加速的作用,即忽略了电热阶段的加速过程。该研究内容中不包含放电电弧与固体推进剂表面之间的烧蚀和电离相互作用。
根据法拉第电磁感应定律,由电容、电极、等离子体组成的放电回路中产生的感应电动势[14]为:
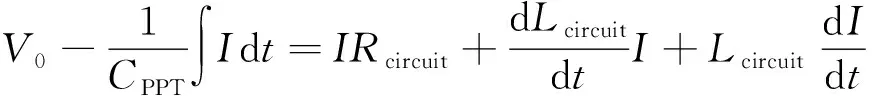
(1)
式中:Rcircuit,Lcircuit,CPPT分别为放电回路中的电阻、电感和电容;V0为初始电压;I为放电电流。电路中的电感和电阻分别来自于电容器、电极以及等离子体。
Lcircuit=Lcapacitor+Lelectores+Lplasma
Rcircuit=Rcapacitor+Relectores+Rplasma
等离子体中产生的电感可以表示为流过等离子体的磁通φB与电流I的比值。流过任意闭合表面的磁通为0,即:
为了计算趋肤效应导致电极上电流密度分布不均匀产生的电感,假设电极由无数个子电极组成,则各子电极之间的电感[15]为:
式中:lsub为电极的长度;wsub为子电极的宽度;δsub为子电极的厚度。各子电极的电阻Rsub[15]为:
式中:σsub为电导率。各子电极之间的互感Mij,mn[15]为:
式中:下标i,j,m,n分别为第1个和第2个子电极的行和列位置;d为两个子电极中心之间的距离。由欧姆定律得V=I(R+iωL),ω为频率,i为虚数单位。放电过程产生的等离子体用磁流体方程组描述为:
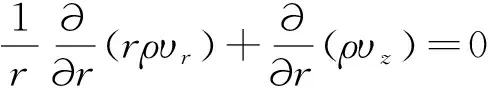
(2)
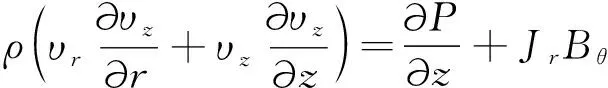
(3)
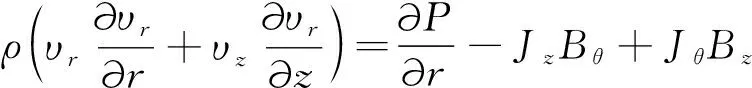
(4)
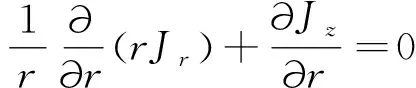
(5)
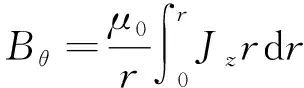
(6)
式中:ρ为等离子体的密度;υ为等离子体的速度;P为等离子体压强;Bθ为流过电极的电流产生的磁感应强度;Bz为外部磁感应强度,计算中设为0;Jr,Jz,Jθ分别为径向、角向和轴向电流,为了简单,假设电流只有Jz分量。由于电子的温度远高于离子的温度,Te≫Ti,因此忽略等离子体中离子对压强的贡献,则等离子体的压强可表示为P≈kbNeTe,式中:Ne为电子的数密度,kb为玻尔兹曼常数,电子的温度由电子的热平衡方程进行描述[16]:
式中:S=πr2为截面积;Qei为电子和离子发生弹性碰撞和非弹性碰撞所损失的能量;q为电子的热通量;κe为热传导系数。由于电流与离子速度有关,因此可以建立等离子体速度与电子速度之间的关系:
式中:αi为归一化的离子电流。采用一维的准中性平衡模型,电离满足如下关系[17]:
式中:kn为电离系数[17]:
式中:σ0=10-20m2;E0=13.6 eV;En为工质从n-1电离态到n电离态所需要的能量。
式中:λn=υ/(knNe);Cn为某一电离态在分布函数中所占份额;r为等离子体与阴极之间的距离。
平均电离态为:
电子密度作为电流的函数写为:
假设满足准中性条件,则由碰撞损失的能量为[17]:
推力器中喷射出的离子所受的洛伦兹力为[14]:
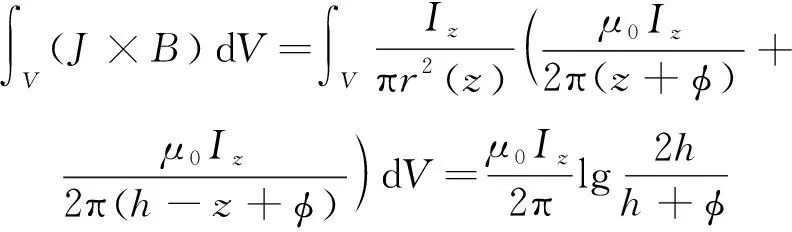
(7)
式中:φ为电极厚度的一半;h为电极间距;μ0为真空中的磁导率。等离子体在洛伦兹力作用下的运动满足牛顿运动方程:
式中:m为等离子体的质量。等离子体质量的变化率则可以表示为离子损失率Γi与放电电流I的函数,即:
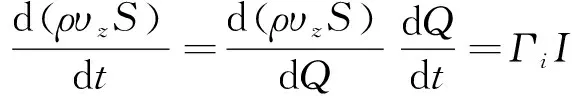
(8)
式中:Q为电容器所带电量。综合上式可以研究初始放电电压、电极间距等参数对脉冲等离子体性能的影响。
1.2 求解方法及边界条件
该模型的求解分为两部分,第一部分由描述等离子体的磁流体方程组式(2)~(6)组成,第二部分由包含电路参数、几何参数等信息的式(1)(7)(8)组成。由于等离子体的密度ρ和等离子质量的变化ΓiI有关,因此磁流体方程组和电路方程耦合在一起。在求解过程中磁流体方程组采用四阶龙格-库塔方法求解。当解收敛时,将收敛的解作为第二部分的初始条件,利用Matlab求解延迟微分方程的dde23库函数进行求解,当计算时间大于设定的时间上限时,计算终止。在计算中,假设初始时刻电路中的电流I(0)=10 A,等离子体的速度为υ(0)=1×10-3m/s,等离子体初始质量为M(0)=1×10-3μg,电子初始温度为1 eV。结合上述初始条件和计算方法就可以获得脉冲等离子体工作过程中各物理量随时间的变化。
2 数值计算结果
2.1 初始电压对PPT的影响
假设PPT推力器电极由纯铜构成,电极厚δ=0.003 m,电极宽w=0.01 m,电极间距h=0.03 m,电容C=4.0 μF,电感L=300 nH,电阻R=35 mΩ,放电频率f=13.6 kHz。图1为不同初始放电电压下推力器放电电流和电压的波形。随着初始放电电压的增加,放电电流幅值具有明显的增加。电流峰值的增加意味着放电能量的增加。对于PPT,其推力等于喷射出粒子所受洛伦兹力和气动压力之和。由于气动压力(热压力)相对较小,PPT的推力约等于离子所受洛伦兹力的大小。在磁场不变的情况下,放电电流的增加意味着粒子所受洛伦兹力的增加,洛伦兹力的增加将导致离子速度的增加,如图2所示。
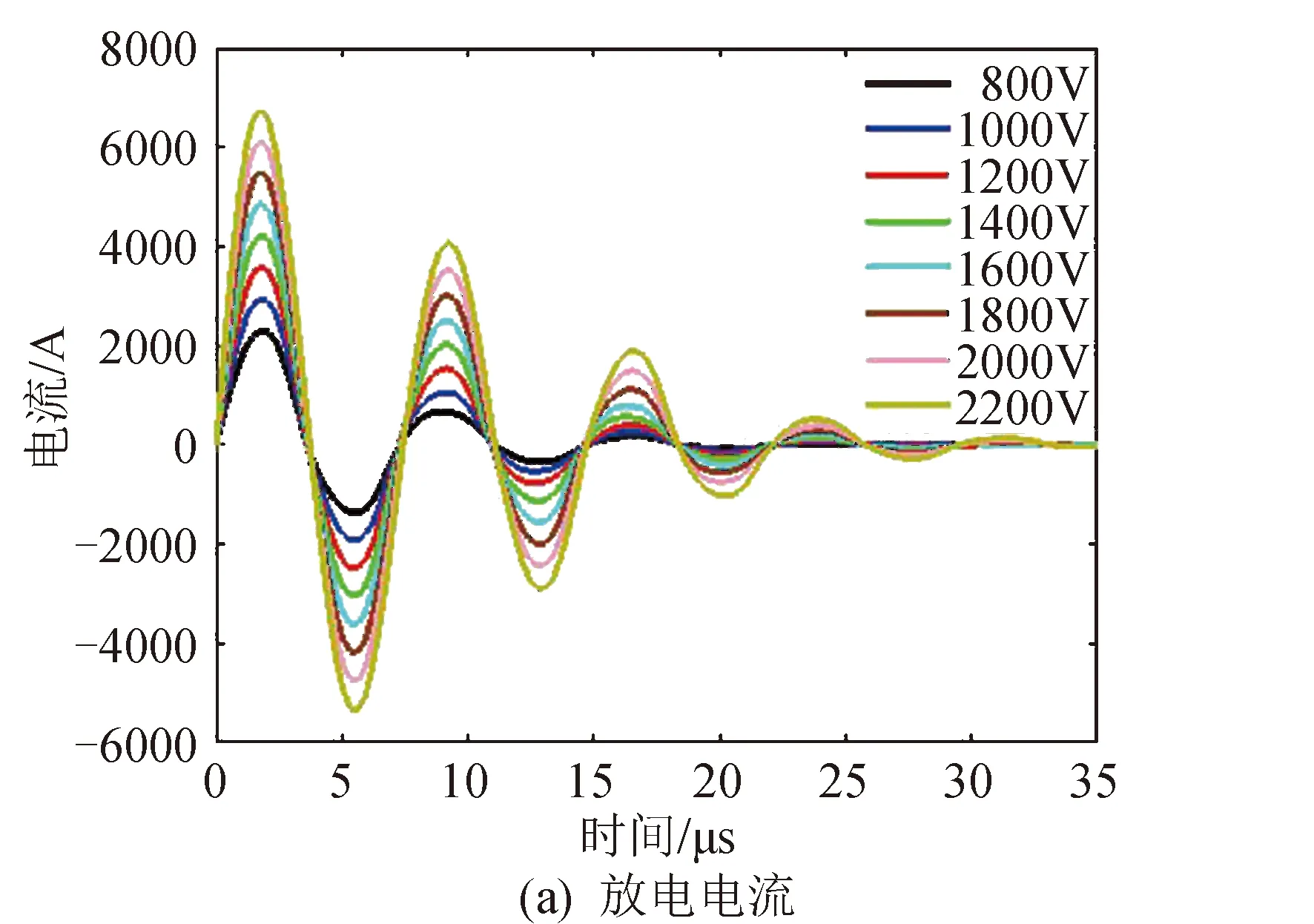

图1 不同初始放电电压下放电电流和电压波形Fig.1 Waveforms of discharge current and voltage with different initial discharge voltages
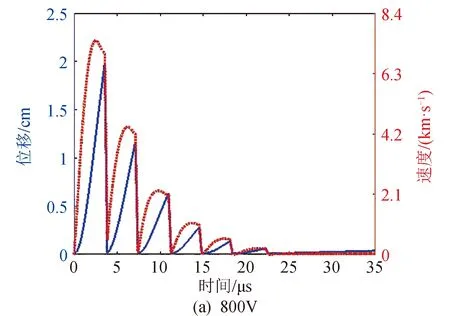
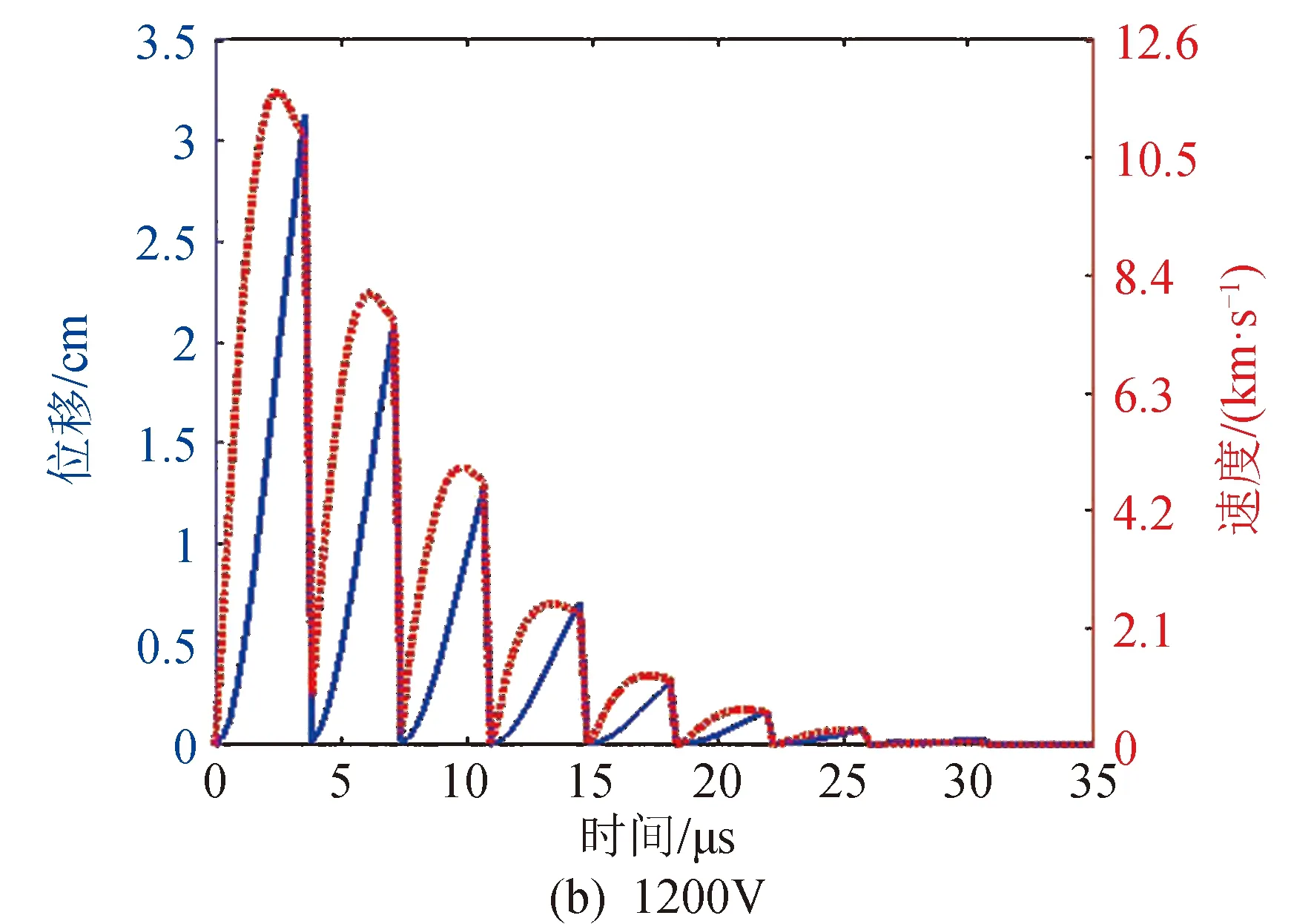
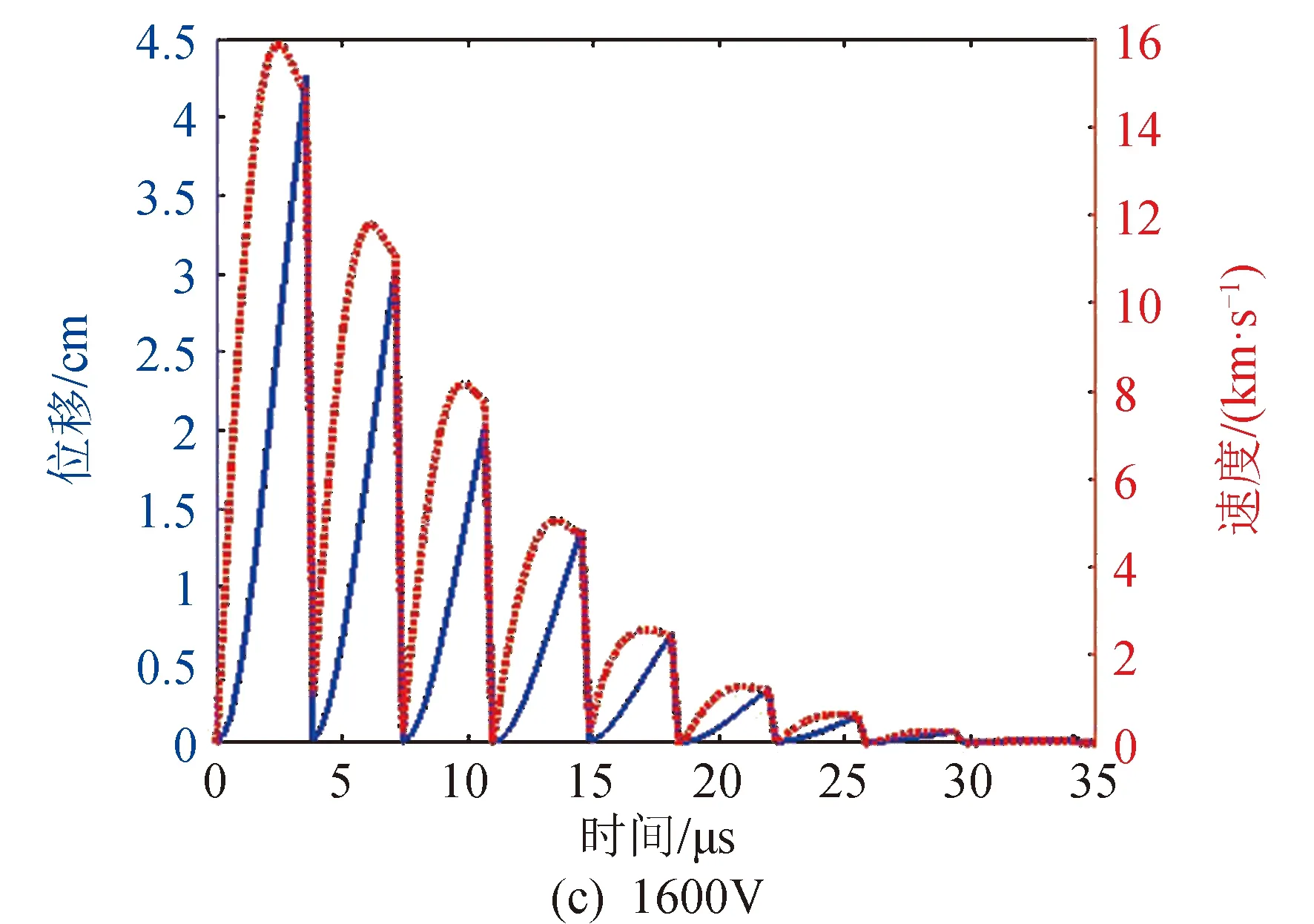
图2比较了初始放电电压分别为800,1 200,1 600,2 000 V四种工况下,等离子体速度和位移随时间的变化。随着初始放电电压的增加,在单个脉冲放电周期内,等离子体的速度和位移都相应的增加。由推力器比冲和元冲量的定义可知,增加粒子的运动速度将导致推力器比冲的增加,如图3所示。
随着初始放电电压的增加,不论是比冲的最大值还是比冲的平均值都随初始放电电压的增加而增加。比冲的增加是由于离子速度的增加。
图4(a)给出了等离子体质量与初始放电电压之间的关系。随着初始放电电压的增加,电离产生的等离子体的质量也随之增加。这是因为放电电压的增加导致电容器在单个脉冲内释放的能量增加,从而在推进剂表面烧蚀、电离产生更多的离子。推力器的元冲量由喷出粒子的质量和速度二者共同决定,增加初始放电电压也将导致推力器元冲量的增加,如图4(b)所示。
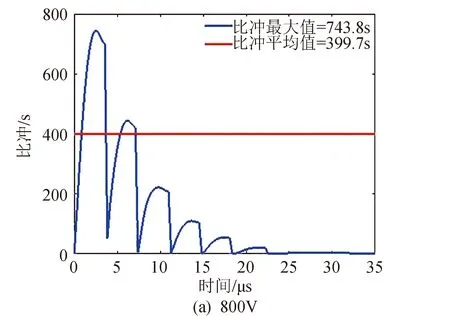

图3 不同初始电压下的比冲Fig.3 The specific impulse with different initial discharge voltages

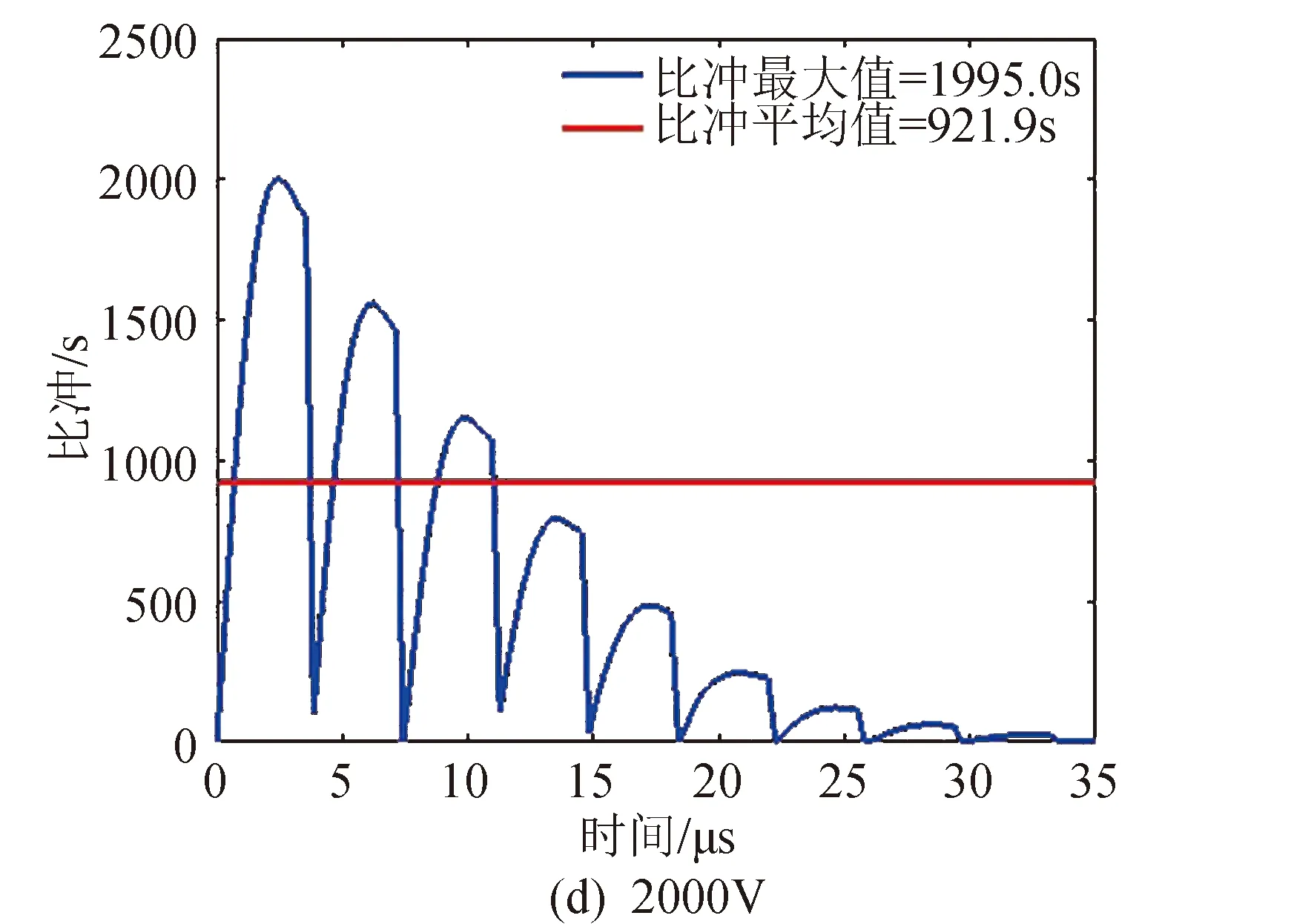
续图3 Fig.3 Continued
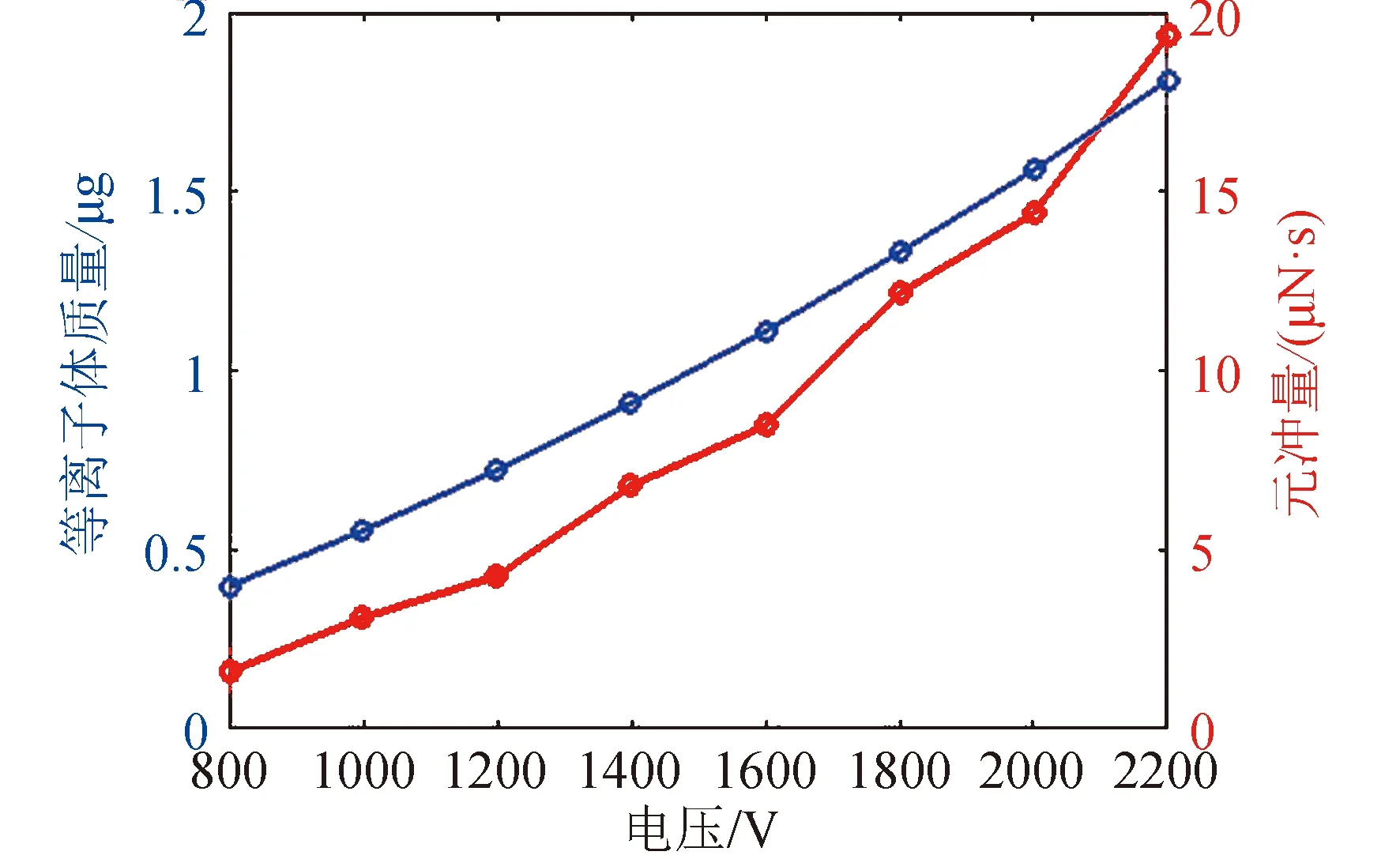
图4 等离子体质量和元冲量随放电电压的变化Fig.4 Plasma mass and impulse bit varing with the initial discharge voltage
图5为放电电压为800 V和1 600 V时的电子密度和温度的分布。观察发现,电子密度分布比较集中。电子密度相对集中的可能原因有:1)放电过程中等离子体主要产生在该区域,导致这一位置电子密度的局部增加;2)二次电子效应。由于电子温度的局部增加,导致等离子体中的离子被进一步电离,离子在被进一步电离的过程中将产生额外的电子,最终导致局部的电子温度和密度增加。
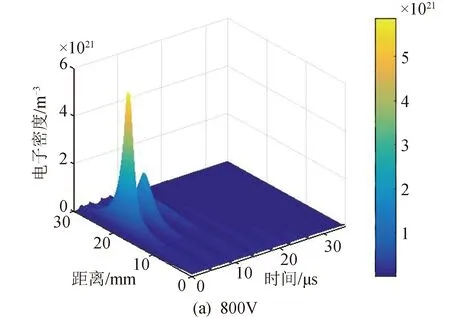
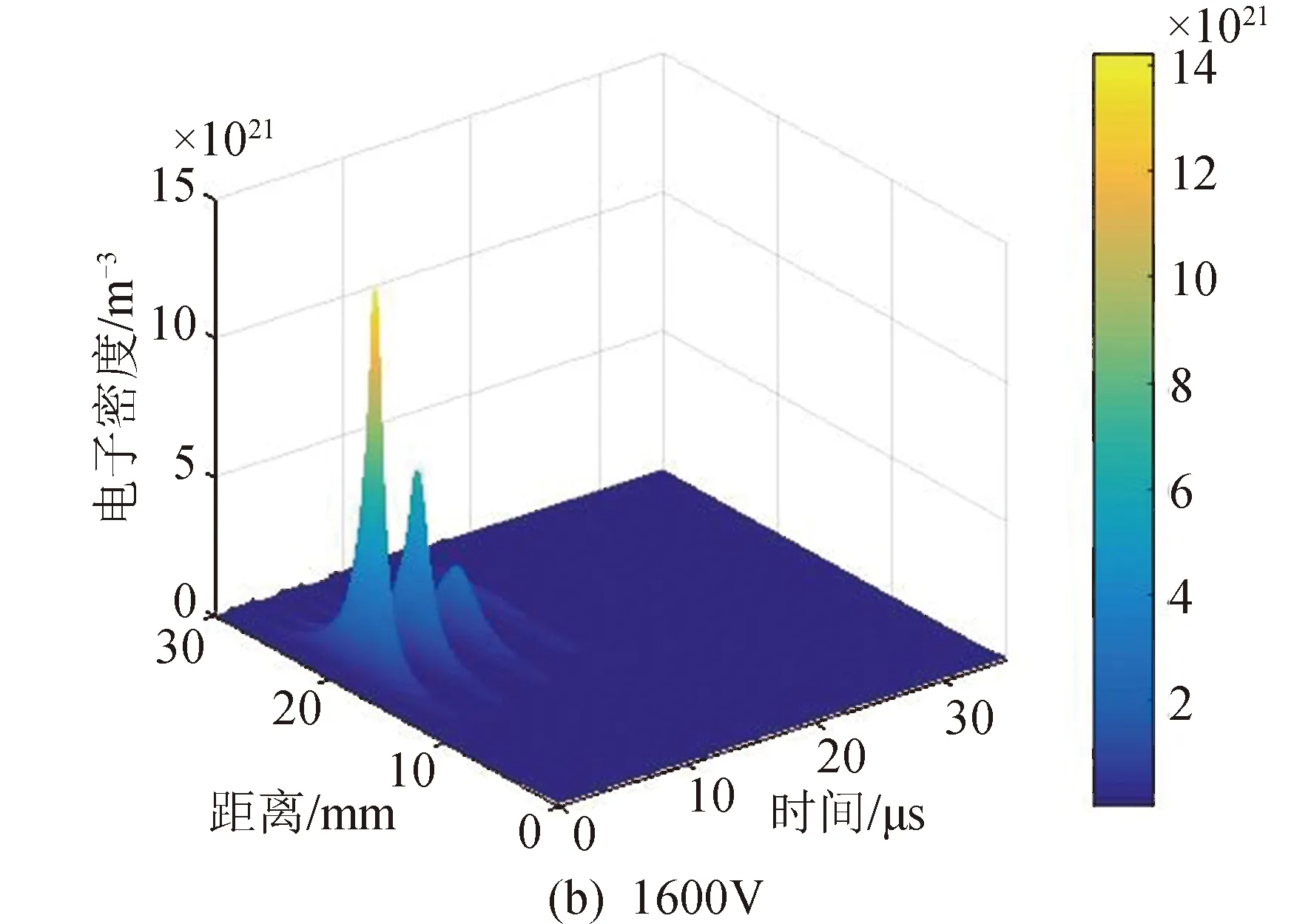

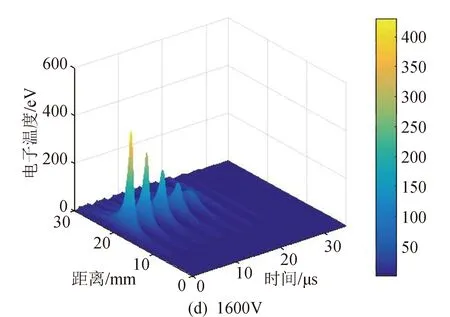
图5 不同初始电压下的电子密度和温度Fig.5 Electron density and temperature with different discharge voltages
图6比较了不同放电电压下离子所受洛伦兹力的大小。随着放电时间的增加,离子所受洛伦兹力逐渐减小,直至为0。这是由于放电电流的幅值随着放电时间的增加逐渐减小。此外,离子所受的洛伦兹力随初始放电电压的增加而增加,导致这一结果的原因是电流幅值随着初始放电电压的增加而增加,如图1(a)所示。
2.2 极板间距对PPT的影响
对于给定电容器类型及极板构型的PPT,电极间距的改变不仅会改变放电通道内电磁场的分布及大小,造成等离子体所受洛伦兹力的改变,而且还改变放电回路参数,造成回路电感及放电通道内等离子体电阻的改变,使系统放电特性发生变化。
电极间距的增大意味着推进剂曝光面积的增加,相应地被烧蚀的推进剂质量也增加。当推进剂烧蚀区域体积保持不变时,等离子体密度的增加将导致放电空间内压力升高,进而导致电热加速效能的提升。图7是在不同电极间距下,放电电流和放电电压波形。计算中,初始放电电压为1 400 V,其他参数与前面所述一致。由图7可知,在其他参数相同的情况下,电极间距在一定范围内的增加将导致等离子体放电电流幅值的增加。
此外,电极间距的变化会影响极间电感和等离子体电阻的大小。图8比较了电极间距分别为0.02,0.03,0.04,0.05 m时等离子体的电感变化,结果表明随着电极间距的增加,等离子体电感相应增加。Guman等[18]给出了平行电极型PPT的电极间距对极间电感的影响:
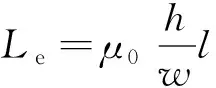
(9)
式中:Le为极间电感;h为极间距离;w为极板宽度;l为极板长度。从式(9)可以看出随着极板间距的增加,极板间等离子体的电感将增加,这与图8结果一致。需要说明的是式(9)仅适用于h≫w的情况。带电粒子由于电磁加速产生的推力[18]为:
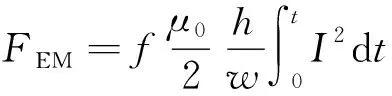
(10)

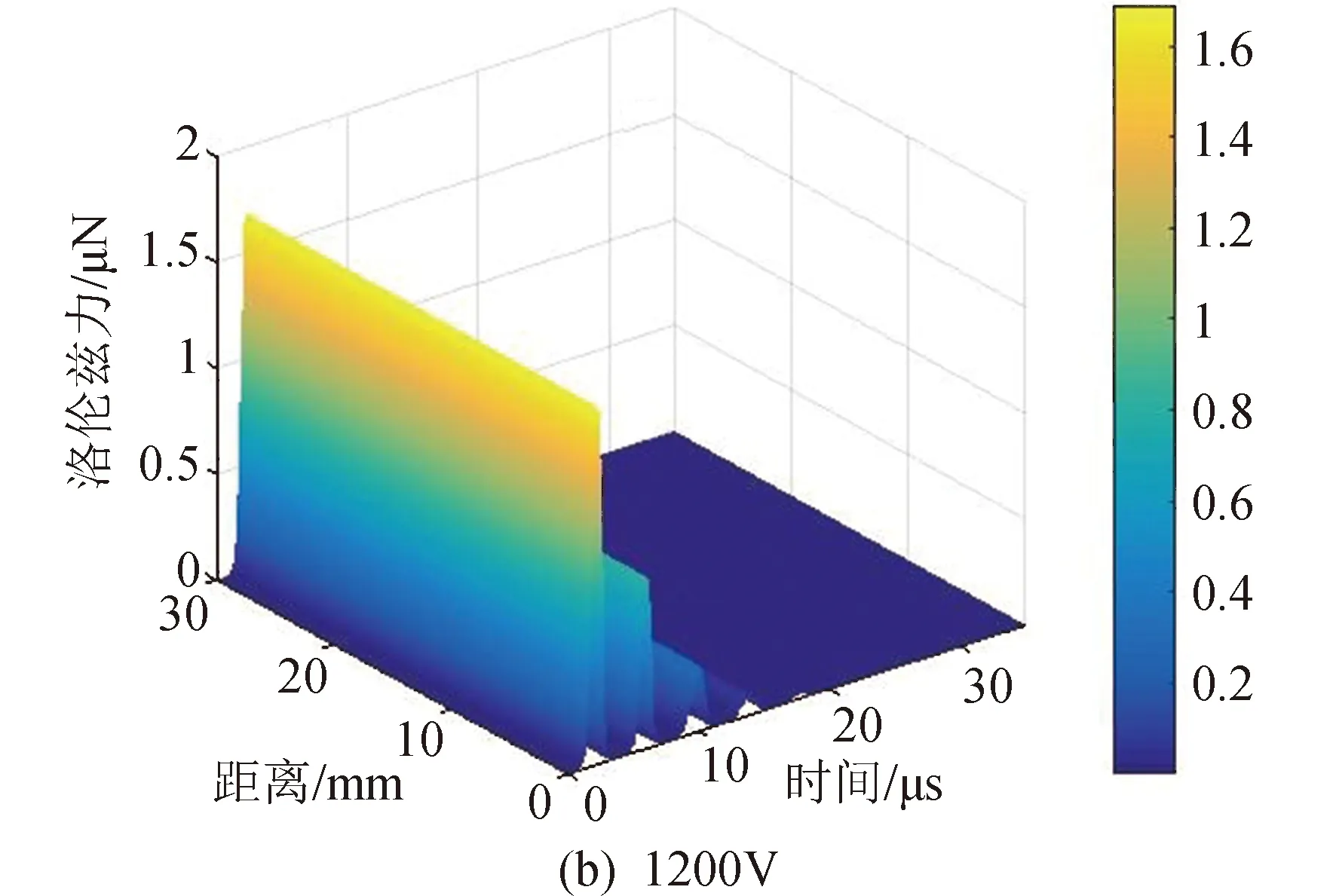
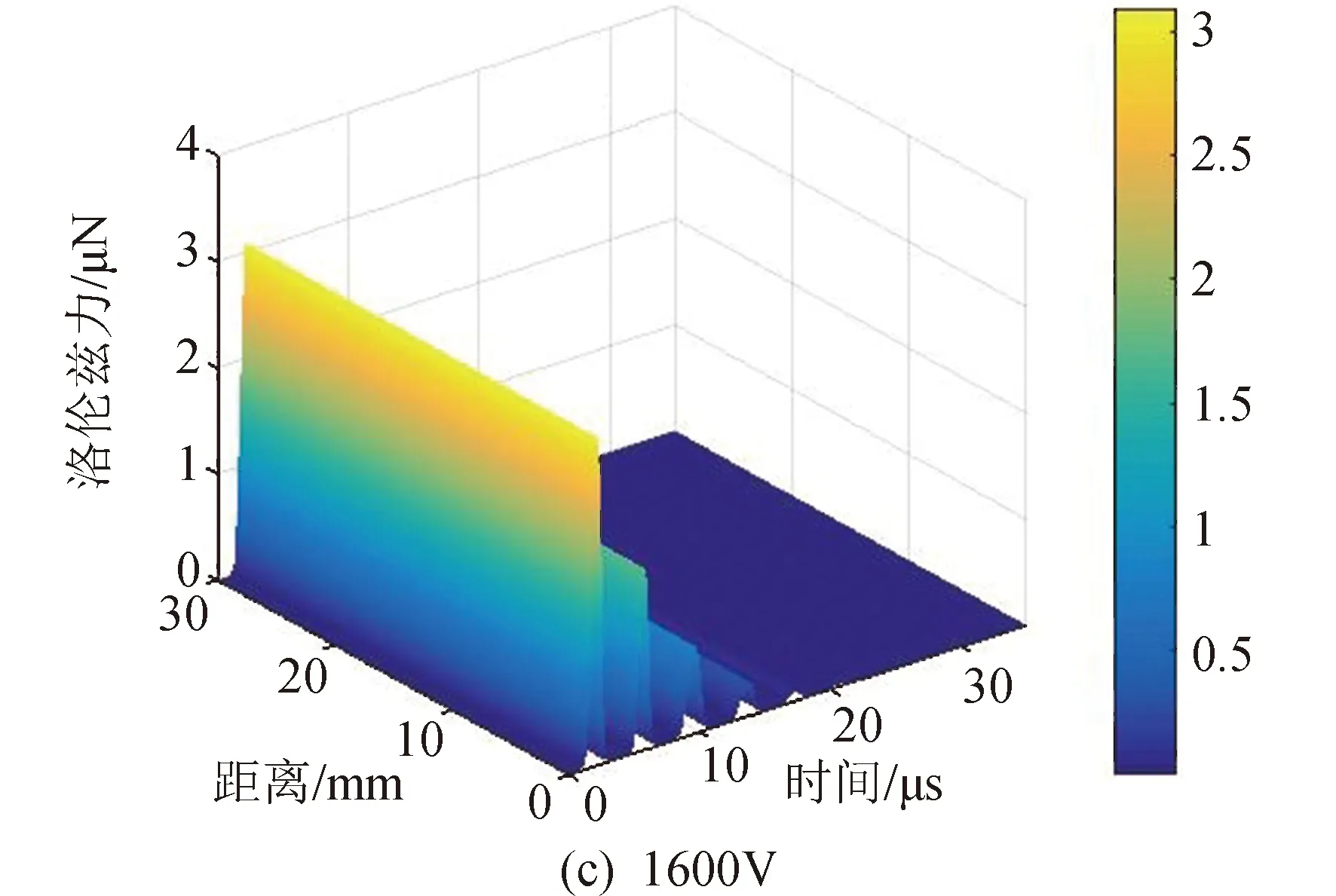
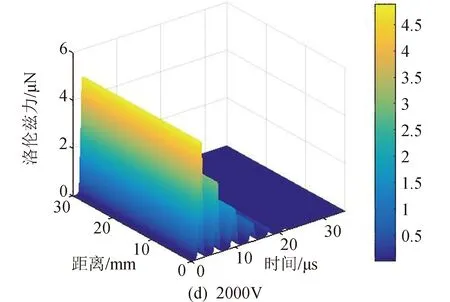
图6 不同初始电压下的洛伦兹力Fig.6 Lorentz forces with different initial discharge voltages
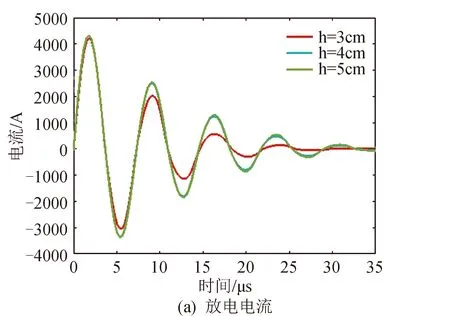
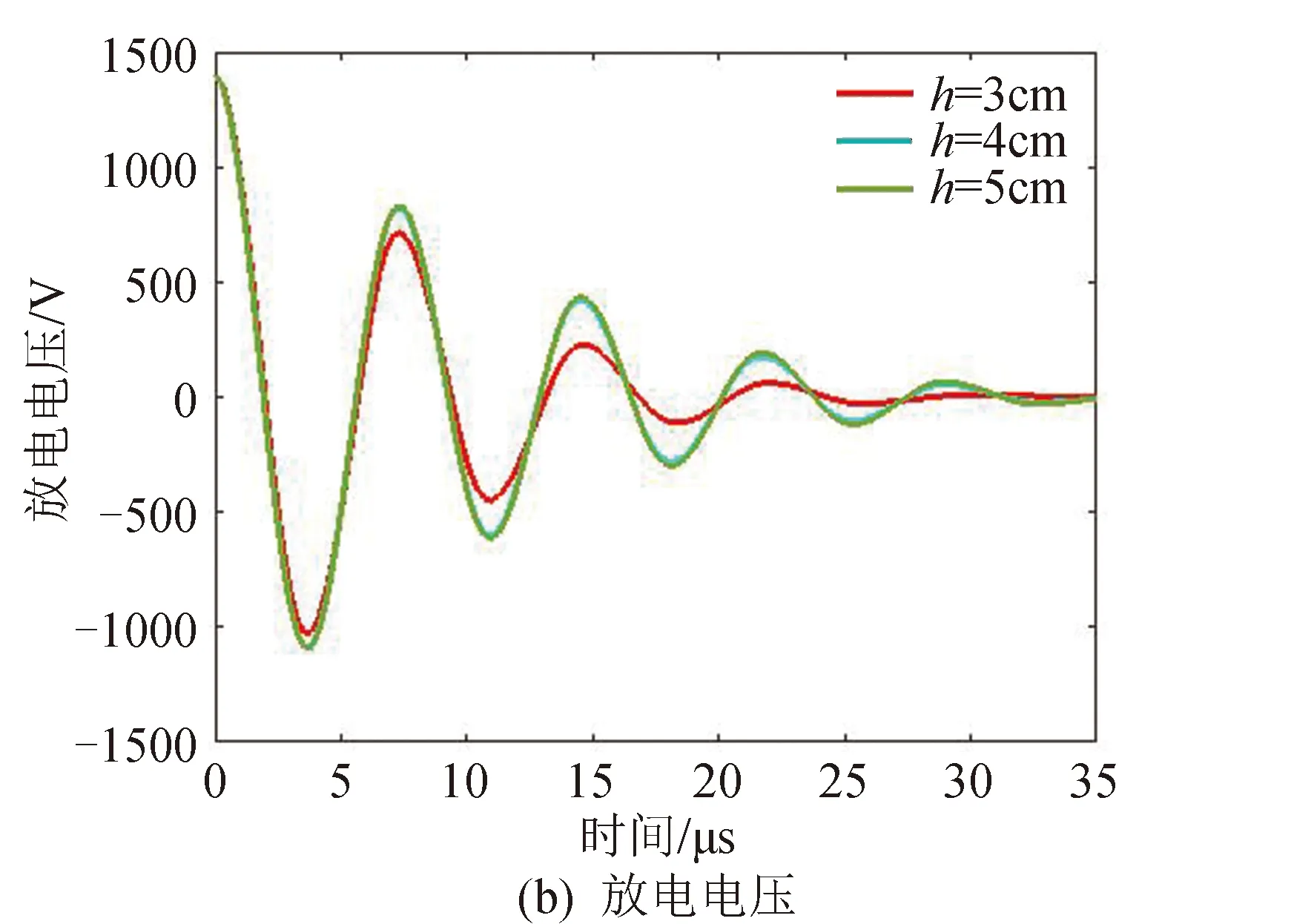
图7 电极间距对放电电流和电压的影响Fig.7 Electrode distance effects on the discharge current and discharge voltage
从式(9)和式(10)可知,当极板距离增加时,极板间的电感和电磁加速产生的推力都将线性增加。此外,从式(10)可知推力与h和w的比值有关。在PPT推力器中,比冲定义为:

(11)
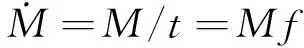
式中:γ为与推进剂有关的恒量,对于聚氟乙烯γ=1.3。比冲还可以表示为:
Ibit为元冲量,定义为:
Ibit=Mυex
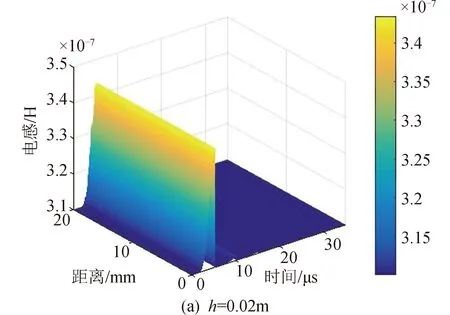

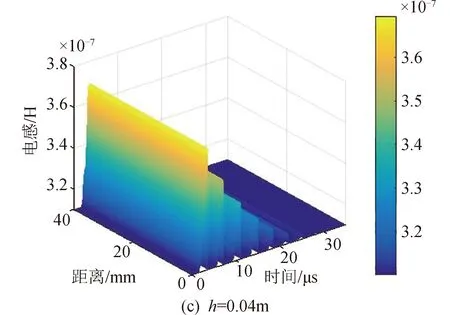
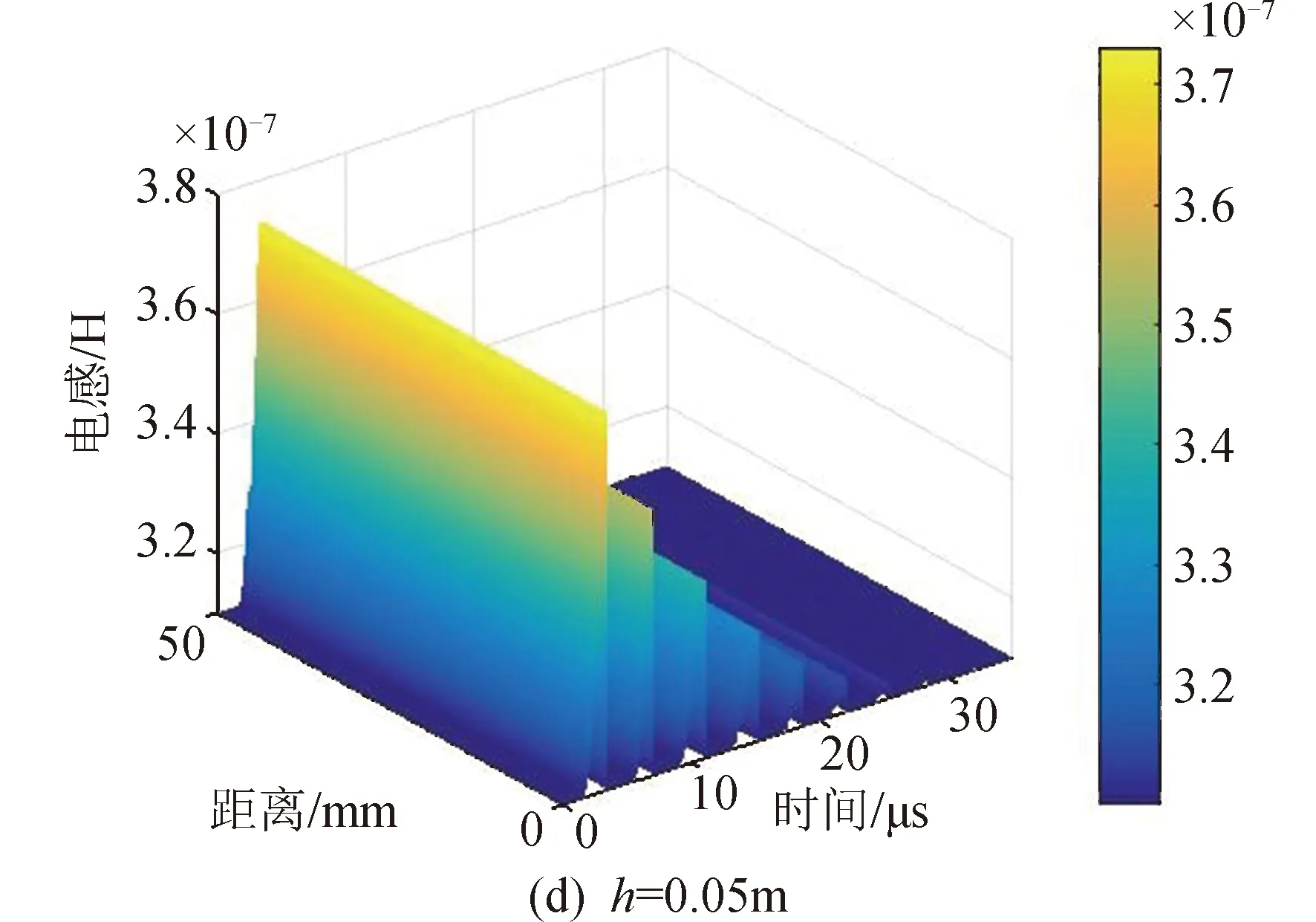
图8 电极间距对回路电感的影响Fig.8 Electrode distance effects on the circuit inductance
式中:υex为推进剂粒子的有效喷射速度,喷射粒子的动能可以表示为:
对于PPT,推力器效率定义为粒子获得的动能与电容储能的比值。因此效率表示如下:
式中:E为电容器储能。因此,由式(10)和式(11)可知,在推力器电极宽度一定的情况下,增加极板间距会使推力器的比冲相应的增加,如图9所示。
由式(10)可知,为了得到较好的电磁加速效果,应选择较大的电极高/宽比,但在实际情况中,电极的间距经常受推力器尺寸、质量和星上空间的限制。采用提高推进剂曝光面积的方法可以提高推功比,并能提高比冲和推力。但由于这种方法消耗大量的推进剂,会降低推进剂的质量利用率,从而降低效率。
与式(10)反映的结果一致,随着极板间距离的增加,由电磁加速产生的推力也随着极板间距的增加而增加,如图10所示。图10比较了电极间距为0.02,0.03,0.04,0.05 m时洛伦兹力的大小。推力器的推力随极板间距h增加是因为h增大,推进剂的暴露面积也随之增大,从而可以产生更多的等离子体,因此推力F提高。但是,随着电极间距h的增大,极板间的阻抗也随之增大,电流振荡的次数减小,击穿困难,放电电弧也越来越难产生,进而造成放电失败。因此,电极间距h存在一个优化值。当电极间距h超过优化值后,推力F将随之降低。此外,电极间距h的选择还应考虑星上空间的限制。
3 结束语
本文采用一维集成电路模型系统地研究了PPT推力器放电电压和电极间距对PPT性能影响。研究结果表明:1)增加推力器放电电压有助于提高推力器的性能,如推力、比冲等。这是由于高的放电电压意味电容器具有大的储能,放电电流的幅值随着放电电压的增加而增加。放电电流的增加使离子所受的洛伦兹力增加,离子喷射速度的增加,从而导致推力和比冲的增加。2)在一定范围内增加电极的高/宽(h/w)比会使推力器的推力和比冲都增加,这是因为改变电极间距会影响等离子体的电阻和电感以及推进剂的暴露面积,从而影响放电周期、放电电流的波形,进而影响推力器的性能。为了研究推力器工作过程中的积碳、工质烧蚀形成的大颗粒等对推力器性能的影响,在后续工作中,需要开展放电电弧与工质表面相互作用的研究。
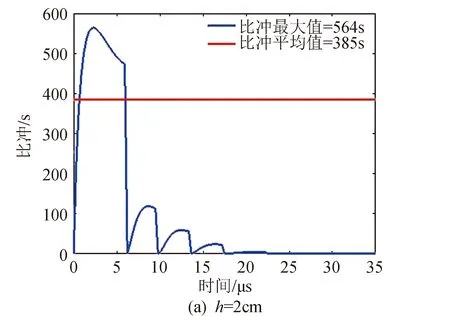
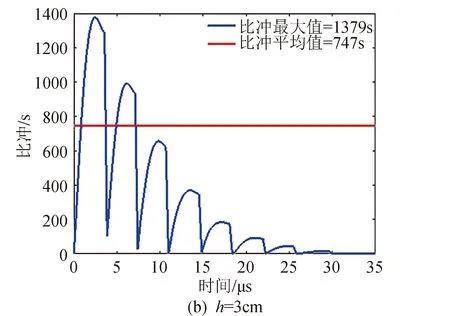
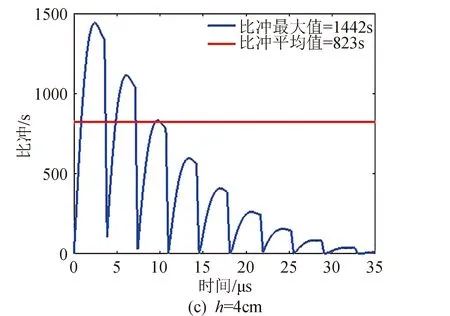
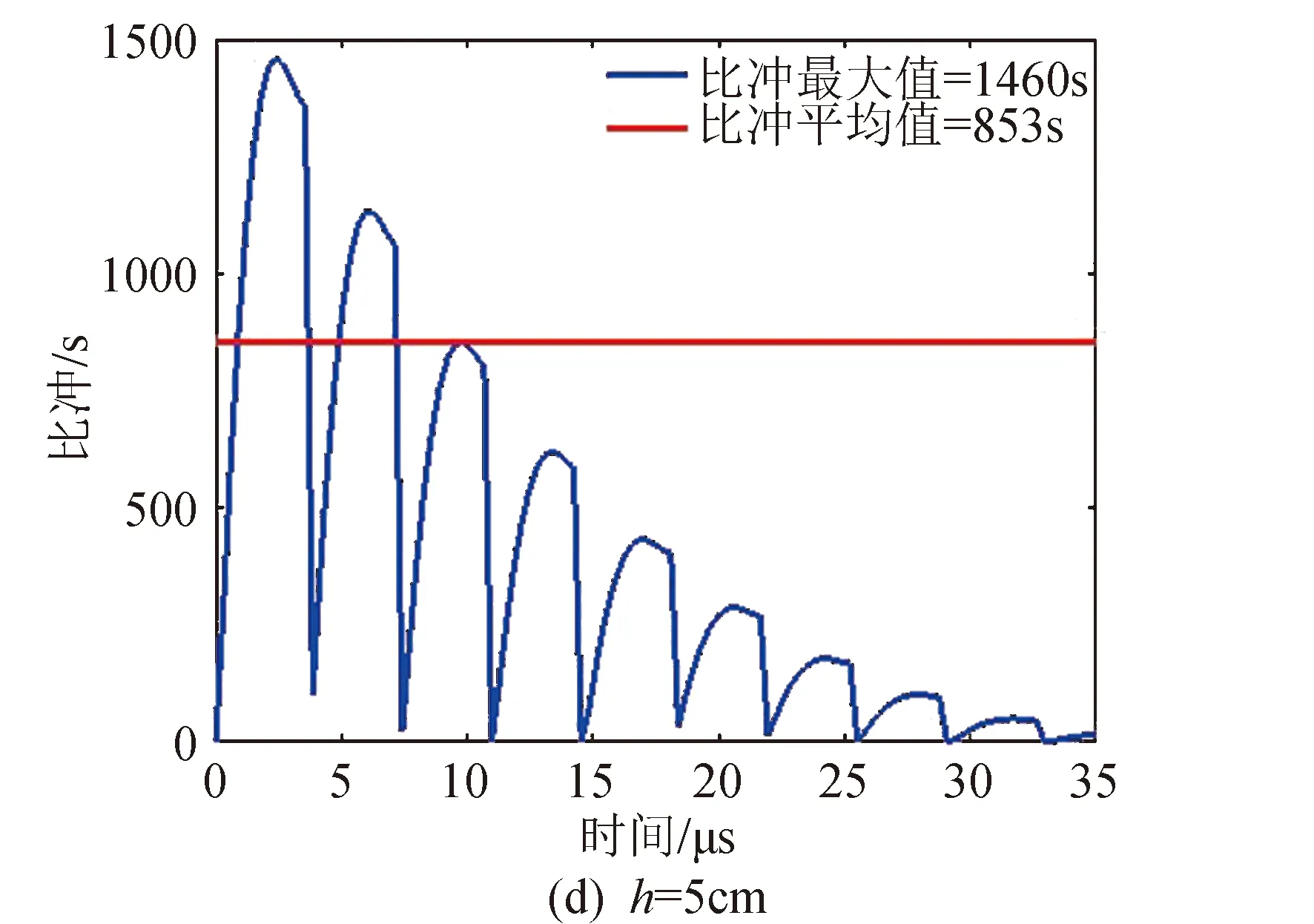
图9 不同极板间距下的比冲Fig.9 The specific impulse with different electrode distances