新冠疫情期间应急物资配送路径优化研究

曲贝贝 王效俐

摘要：疫情期间保证应急物资的配送是严防严控的重要环节，考虑到新冠疫情传染性强且具一定致死率，新冠应急物资在配送方面应注重时效性。在满足载重量和需求量以及盡可能满足时间窗要求的基础上建立基于变异蚁群算法的物流配送路径优化模型，并通过实例验证算法可行性。从求解过程和结果来看本研究提出的模型和算法找到的路径是较优的。

Abstract： Ensuring the distribution of emergency materials during the epidemic is an important part to control the epidemic. Timeliness should be paid attention to in the distribution of emergency supplies considering to highly contagious and lethal of the COVID-19 epidemic. To meet the time window requirements as much as possible， a logistics distribution route optimization model based on the mutation ant colony algorithm is established， and the feasibility of the algorithm is verified through examples. From the results， the path found by the model and algorithm proposed in this study is better.

关键词：疫情应急物资;蚁群算法;路径优化;变异因子

Key words： epidemic emergency supplies;ant colony algorithm;path optimization;mutation factor

中图分类号：R197.32                                    文献标识码：A                                  文章编号：1006-4311（2020）31-0099-04

0  引言

2019年12月以来，湖北省武汉市发现多起不明原因肺炎，现已证实为一种新型冠状病毒感染引起的急性呼吸道传染病。新冠病毒的传染力较强，根据世卫组织的数据，新冠病毒的基本再生数（R0）在1.4-2.5之间（有资料统计为1.4-5.5）。这意味着，平均每个新冠病毒确诊病例会感染1.4-2.5（或5.5）个人[1]。同时，新冠病毒具一定致死率，截至9月29日全球确诊病例数高达3346万，死亡病例数高达100万，致死率约在3%远高于普通流感[2]。新冠疫情暴发后，全国应急物资运输保障中出现了运输通道受阻、应急物资分拨不畅等问题，导致生活物资和必要的医疗物资出现供需失衡的问题。疫情的特殊性使得生活医疗物资的配送具有一定的时效性，可认为品质和时间呈负相关，因此改进物流配送，寻求最优的物流配送路径，提高配送效率和准时性是保证新冠期间物资配送的重要研究方面。9月26日的第二届海峡两岸国际医疗与特需服务发展大会上，张文宏表示以现在疫情蔓延态势来讲，新冠病毒已经变成“常驻病毒”，全球疫情发展至今，随时有可能出现一个“小火花”，即局部性的疫情小爆发。这意味着我们应当随时对局部性疫情爆发做好准备，一旦出现疫情增长势头，迅速采取防控措施，同时保证相关医疗生活物资及时供应，以消除疫情扩散可能[3]。本文的研究将针对新冠期间应急物品配送车辆从物资配送中心到各个医院的路径进行优化研究。研究的目的在于改进物流配送从中心仓库到各医院的环节，在满足医疗需求的条件下，寻求最优配送路径。

1  蚁群算法简介

蚁群算法是由意大利学者Dorigo、Maniezzo等人于20世纪90年代首先提出来的。他们发现蚁群可以通过释放“信息素（pheromone）”找到最短到达食物源的路径，这即是蚁群算法。如果在给定点，一只蚂蚁要在不同的路径中选择，那么，那些被先行蚂蚁大量选择的路径（也就是信息素越浓的路径）被选中的概率就越大，信息素越浓意味着路径越短，也就意味着找到了一个更好的解。

蚁群算法在解决问题上主要有以下的优点：①蚁群算法与其他启发式算法相比，在求解性能上，具有很强的鲁棒性。②对算法模型稍加修改，便可以应用于其他问题，具有搜索较好解的能力。③蚁群算法是一种基于种群的进化算法，具有本质并行性，易于并行实现[4]。

变异是遗传算法中一个重要的过程，变异运算用来模拟生物在自然的遗传环境中由于各种偶然因素引起的基因突变，我们在这里中引入变异操作，使得蚂蚁在初始基因组合以外的空间进行搜索，避免进化过程在早期就陷入局部解而进入终止过程，使之在尽可能大的空间中获得质量较高的优化解[5，6]。

2  模型建立

2.1 数据收集  本文的研究收集了10个配送点的位置坐标，需求量，配送的时间窗，可接受时间窗和卸货所需要的时间数据。如表1和表2所示。

由于配送点对于疫情应急物资具有时间窗要求，并且时间窗分为要求时间窗和可接受时间窗。为了满足时间窗要求，本文在研究中对配送时间引入惩罚值。如果配送车辆在要求时间范围内到达，则惩罚值为0，如果配送车辆超出要求时间但是在可接受时间范围内到达，则惩罚值和时间之间呈线性相关[7]，如图1所示。

2.2 数学模型

2.2.1 模型假设  在构建配送的数学模型之前，对配送点的需求量，车辆的运行路线，车速，载重量等相关条件进行如下假设：①單一配送中心，配送中心的总货量大于所有医院的需求量;②车辆从配送中心出发，完成任务后返回配送中心;③已知医院量、需求量、地理位置及时间窗;④每个医院每日仅被配送1次，所有医院都能得到配送;⑤车辆匀速行驶，速度为60km/h;⑥车辆只负责送货，即单向物品流向;⑦所有医院所需商品都由配送中心供给，医院之间不存在相互调剂的情况;⑧各医院的需求量确定，并在一定时期内相对稳定;⑨冷藏车所载货物的质量不超过其载重量[8]。

2.2.2 参数设置

qi：医院i的需求量;D：表示冷藏车辆的载重量;dij：表示任意2个医院i、j之间的距离;Rkr：表示第r条路径上第k个医院的编号;ti：表示到达医院i的时刻，i∈N;ti1：表示医院i可接受时间窗的前一个时刻，i∈N;ti2：表示医院i可接受时间窗的后一个时刻，i∈N;Vi：医院i的时间窗处罚值，i∈N;Li：表示医院i的卸货时间，i∈N。

2.2.3 约束条件  考虑到新冠疫情的传染风险，在应急物资配送过程中每个配送点只配送一次，不存在多次配送最后总的配送量达到需求量的情况。车辆行驶的路径的起点和终点均为配送中心。最后使得配送路程的总距离和时间窗惩罚值最小[9]。

用C 表示配送总距离，目标函数下：

约束条件如下：yi=1，i∈N表示每个医院只被服务1次;xij=0，i=j∈N表示不能重复服务同一医院;表示到达连续服务的2个医院时刻的递推关系;保证冷藏车到达医院的时刻满足医院可接受的时间窗;表示每条路径的出发点和终点均为配送中心;

表示每个医院的时间窗惩罚值。

2.3 研究模型  针对该配送问题采用混合蚁群算法，结合蚁群算法和遗传算法，在蚁群算法的基础上，增加遗传算法中的变异算子，同时增加参数自适应，以避免陷入局部最优。

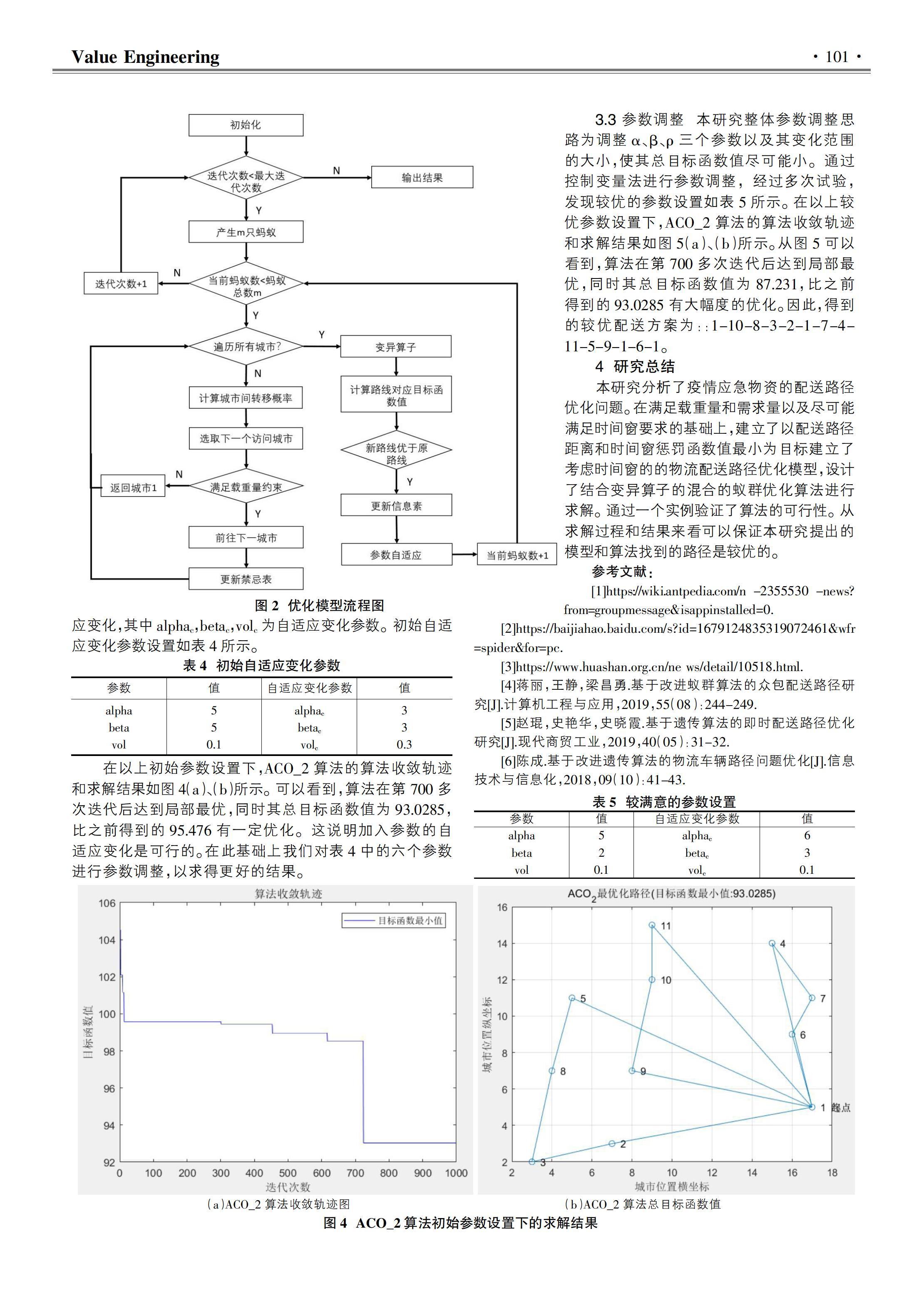
具体模型如图2所示。首先进行初始化，在每一次迭代中，产生m只蚂蚁，对于每只蚂蚁，判断其是否遍历所有城市，如果没有，计算城市间转移概率，选取下一个访问城市，判断是否满足载重量约束，若不满足，则返回城市1，重新计算概率选取城市，若是满足约束，则前往下一个城市，并更新禁忌表，如果遍历了所有城市，对结果进行变异操作，计算变异后的路线对应的目标函数值，如果新路线优于原路线，则采用新路线，若不优于，则放弃变异结果，再更新信息素，进行参数自适应。当所有蚂蚁完成后，增加迭代次数，循环操作，直至迭代次数达到最大迭代次数，然后输出结果。模型如图2所示。

3  数据分析

3.1 初始参数条件算法求解结果  为验证算法的有效性，本研究将算法使用matlab实现，模型中的初始相关参数见表3。参数优化的目标是使时间窗惩罚成本和配送路径之和的总目标函数值最小。在初始参数设置下，得到的实现结果如图3所示。从图3（a）可以看到，使用传统蚁群算法（ACO_1算法）解决本研究问题时容易过早地陷入局部最优，导致目标函数值偏大，未能得到满意解。因此，我们在蚁群算法基础上加入了遗传算法中的变异因子（ACO_2算法），从图3（b）和（d）可以看到，加入遗传因子后，算法收敛轨迹和总目标函数值均得到一定改善。因此本研究在ACO_2算法基础上进行改进和参数调整。

3.2 参数自适应变化  在ACO_2算法基础上，加入参数的自适应变化，具体如下所示：

在每一次迭代计算后，α、β、ρ这三个参数都会发生自适应变化，其中alphac，betac，volc为自适应变化参数。初始自适应变化参数设置如表4所示。

在以上初始参数设置下，ACO_2算法的算法收敛轨迹和求解结果如图4（a）、（b）所示。可以看到，算法在第700多次迭代后达到局部最优，同时其总目标函数值为93.0285，比之前得到的95.476有一定优化。这说明加入参数的自适应变化是可行的。在此基础上我们对表4中的六个参数进行参数调整，以求得更好的结果。

3.3 参数调整  本研究整体参数调整思路为调整α、β、ρ三个参数以及其变化范围的大小，使其总目标函数值尽可能小。通过控制变量法进行参数调整，经过多次试验，发现较优的参数设置如表5所示。在以上较优参数设置下，ACO_2算法的算法收敛轨迹和求解结果如图5（a）、（b）所示。从图5可以看到，算法在第700多次迭代后达到局部最优，同时其总目标函数值为87.231，比之前得到的93.0285有大幅度的优化。因此，得到的较优配送方案为：：1-10-8-3-2-1-7-4-11-5-9-1-6-1。

4  研究总结

本研究分析了疫情应急物资的配送路径优化问题。在满足载重量和需求量以及尽可能满足时间窗要求的基础上，建立了以配送路径距离和时间窗惩罚函数值最小为目标建立了考虑时间窗的的物流配送路径优化模型，设计了结合变异算子的混合的蚁群优化算法进行求解。通过一个实例验证了算法的可行性。从求解过程和结果来看可以保证本研究提出的模型和算法找到的路径是较优的。

参考文献：

[1]https：//wiki.antpedia.com/n-2355530-news？from=groupmessage&isappinstalled=0.

[2]https：//baijiahao.baidu.com/s？id=1679124835319072461&wfr

=spider&for=pc.

[3]https：//www.huashan.org.cn/ne ws/detail/10518.html.

[4]蒋丽，王静，梁昌勇.基于改进蚁群算法的众包配送路径研究[J].计算机工程与应用，2019，55（08）：244-249.

[5]赵琨，史艳华，史晓霞.基于遗传算法的即时配送路径优化研究[J].现代商贸工业，2019，40（05）：31-32.

[6]陈成.基于改进遗传算法的物流车辆路径问题优化[J].信息技术与信息化，2018，09（10）：41-43.

[7]张云川，邹婷.生鲜食品冷链物流配送路径优化[J].江苏农业科学，2019，47（03）：315-319.

[8]魏凯.改进遗传算法在软时间窗车辆路径问题中的应用[D].安徽工业大学，2013.

[9]李汝佳.基于蚁群算法的旅游路线规划问题研究[J].电脑知识与技术，2019，15（8）：137-140.