横观各向同性土体挡土墙被动土压力研究

陈 涛，杨雪强，刘 攀，郑丽婷，周若洋

（广东工业大学 土木与交通工程学院，广东 广州510006）

当前朗肯土压力和库仑土压力两大经典理论仍被广泛采用来计算土压力[1]，但这两种经典计算方法得到的土压力分布曲线与实际不符。Tsagareli[2]和Fang[3]等通过大量试验证明挡土墙墙背后的土压力呈曲线分布。

随着计算机技术的发展，很多学者借助有限元软件来研究土压力。陈页开等[4]对土体采用弹塑性模型，讨论了不同位移模式下的土压力，得出墙后土压力非线性分布作用在挡墙上是一个渐变屈服的过程，且只有当墙后土体形成贯通塑性区才达到极限状态。李秀梅[5]运用离散元对挡土墙土压力进行模拟得出土压力分布与位移模式有关。

以上研究虽然是对两种经典理论进行了修正和拓展，但仍然是假定填土为各向同性材料下进行探讨，然而在自然固结的土体中，通常大主应力是竖向的，微观上看颗粒长轴的排列趋于水平方向为主。这时，黏土具有横观各向同性性质，竖向轴就是其对称轴。也就是说，天然固结土体在水平面上的物理力学性质是各向同性的，而在任意平面上的性质将随该平面与水平面的夹角而变化[6]。

本文将从微观组构张量角度出发，考虑平动位移模式[7-8]引起墙后土体大主应力方向与沉积面法线方向偏转而导致土体强度参数c、φ的变化以及研究多种因素等对被动土压力的影响。

1 横观各向同性土体强度参数表达式

1.1 组构张量理论

本文将参考杨雪强等[9-10]定义的各向异性状态参数A，在Mohr-Coulomb强度准则的基础上，建立考虑抗剪强度参数c和φ各向异性的表达式，可以将土的抗剪强度指标c和φ看作为各向异性状态参数A的函数：

其中，Ac和Aφ分别为粘聚力和内摩擦角的各向异性参数，可由式(1)分别确定；c0、φ0、dj和bj分别为待定的材料参数。

1.2 最小二乘法

为求得参数a0,a1,a2,a3, ,ak的值，分别对a0,a1,a2,a3, ,ak求偏导，得到k+1个等式，要求满足

2 挡土墙土压力有限元计算模型

2.1 几何模型

视重力挡土墙的土压力计算为平面应变问题，使用ABAQUS有限元软件分析。采用混凝土材料挡土墙，墙高H为5.0 m，顶部宽度1 m，底面宽度3 m，挡墙背面竖直、光滑。回填土的水平长度为4H。考虑到它对挡土墙的土压力影响很小，地基是坚硬的基础，地基的厚度与墙高相同，长度为28 m。挡土墙、土体和地基均采用四节点平面应变单元CPE4。墙顶和自由表面上的节点是自由的，左右土体边界面节点位移在水平方向上受约束；底部边界面节点位移被水平和垂直约束[12]，如图1所示。

图1 挡土墙模型的应力示意图Fig.1 Stress diagram of retaining wall model

2.2 力学参数

重力式混凝土挡土墙可视作弹性材料考虑。重度25 kN/m3，挡土墙材料的弹性模量为2.5×105MPa，泊松比μ为0.16；基础取弹性，弹性模量为3×103MPa；土体选用黏性土，选用Mohr-Coulomb模型，采用非关联流动法则计算，剪胀角 ψ=0°，取土体重度γ=18 kN/m3。挡土墙与基础之间的摩擦单元设置为0.22，土壤和基础通过耦合约束接触，挡土墙的背面设置为平滑或粗糙接触。

2.3 土体参数确定

土体参数取Kurukulasuriya等[13]得到最大主应力方向与沉积面法向成不同倾角的土试样，由实验得到抗剪强度参数如表1，模型如图1所示。

表1 抗剪强度参数Table 1 Shear strength parameters

图2 c预测值与实验值的关联Fig.2 Correlation between predicted and experimental values for c

图3 φ预测值与实验值的关联Fig.3 Correlation between predicted and experimental values for φ

3 横观各向同性土体挡土墙土压力的有限元分析

3.1 各向同性

取α=0°(即沉积面水平)、抗剪强度参数c=10.1 kPa、φ=25.3°作为本文的土体强度各向同性参数。通过ABAQUS有限元计算可知墙背光滑时水平位移为0.2 m(位移比4%)，即土体达到被动极限破坏时总被动土压力为1817.949 kN/m，墙背粗糙(δ=2φ/3)时水平位移为0.25 m(位移比5%)，总被动土压力为2 468.389 kN/m。

3.2 位移一次施加

将挡墙的水平位移0.2 m(墙体位移比为4%)一次性全部施加，选用α=0°(即沉积面水平)的抗剪强度，参数c=10.1 kPa、φ=25.3°, 利用 ABAQUS计算位移一次施加后土体塑性分布如图4所示。

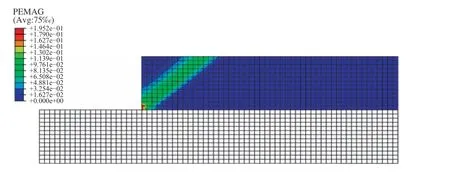
图4 位移比为4%的塑性应变Fig.4 Plastic strain with a displacement ratio 4%

下面仅给出图5位移一次施加是如何利用excel划分不同区块的(多次位移原理是一样)，首先根据模型尺寸大小可以将土体划分成50×13个网格单元，然后对ABAQUS施加0.2 m的水平位移，软件可算出650个网格单元对应的σx、σy及τxy，将结果导出生成excel，将每个网格单元3个应力转化成一个大主应力方向偏转沉积面法向的角，将这个偏转角度相近的划为一个区块，excel可直接算出该区块的平均角度，可被分成3块区域，使用这个平均角度加上之前拟合的式(5)可算出任意角度相对应的强度参数。

图5 分块图像Fig.5 Block image

图5为分块后的挡墙模型,表2为各区块修正后的强度参数。

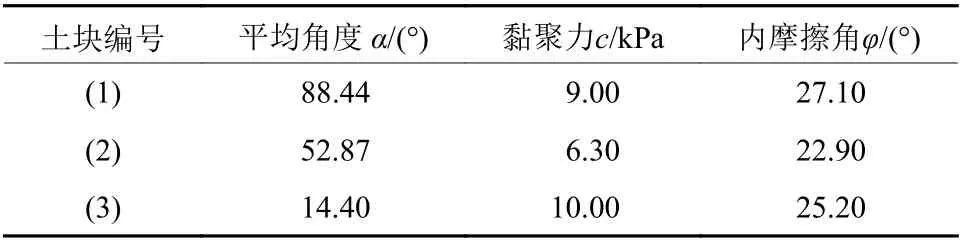
表2 分块强度参数Table 2 Block strength parameters

3.3 位移多次施加

将挡墙的水平位移分三步施加于模型中，取得分块后的模型，代入相应新的强度参数ci、φi后进入下一步位移施加。ABAQUS做多次的试算后，得出第一步位移施加值为0.02 m(墙体位移比为4‰)，土体开始产生较小的塑性应变，如图6所示，分块后图像如图7所示。

图6 位移比为4‰的塑性应变Fig.6 Plastic strain with a displacement ratio 4‰

将表3强度参数代入图7，施加第二步位移值为0.07 m(位移比为1.4%)，结果如图8所示。二次施加位移后，土体内部的应力大小和方向已经发生了变化，利用在excel中算出的每个土体网格单元的大主应力方向角，对模型进行分块处理如图9所示，方向角α如表4所示。

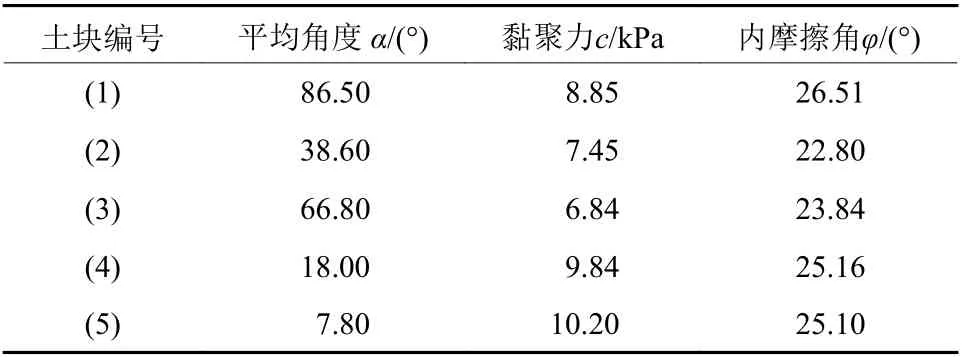
表3 分块强度参数Table 3 Block strength parameters

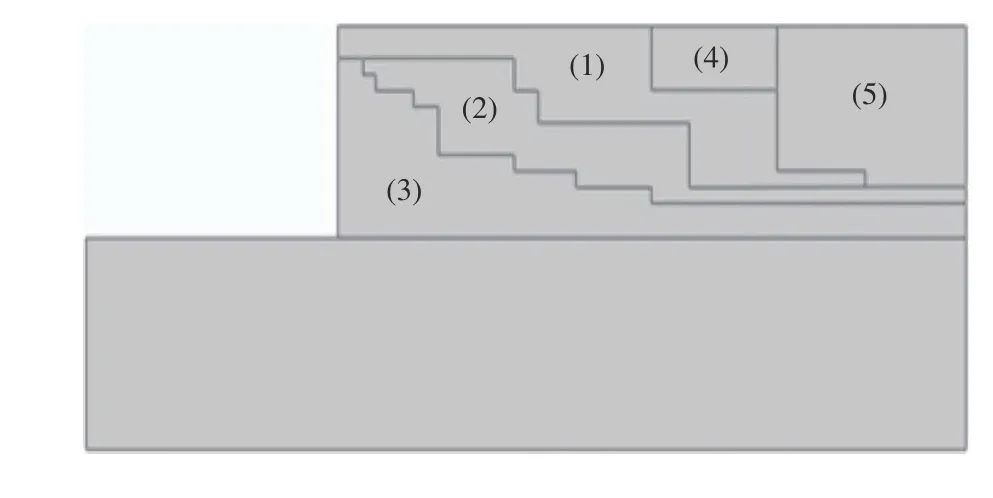
图7 分块图像Fig.7 Block image

图8 位移比为1.4%的塑性应变Fig.8 Plastic strain with a displacement ratio 1.4%

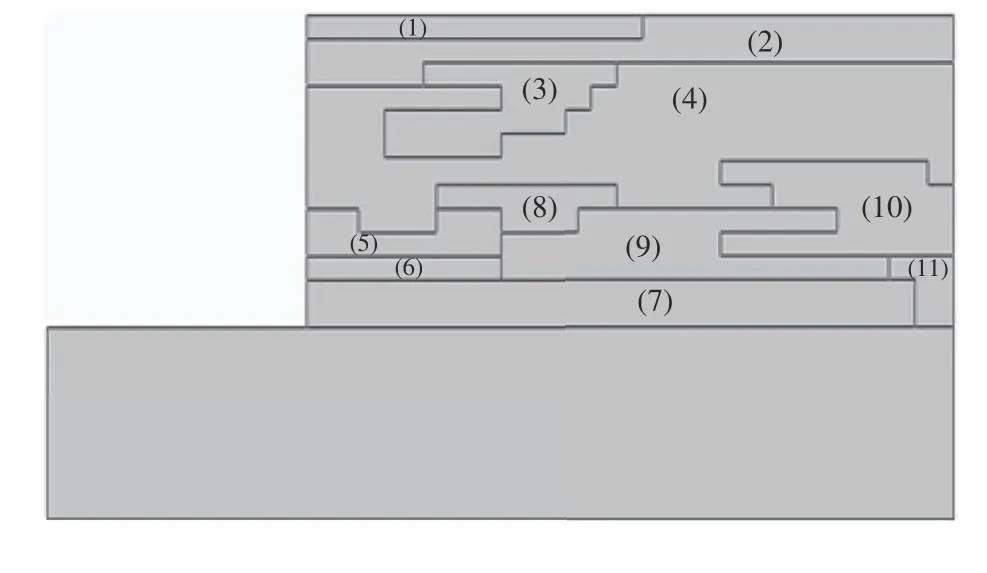
图9 分块图像Fig.9 Block image

表4 分块强度参数Table 4 Block strength parameters

将表4的强度参数代入图9中，施加第三步位移值为0.13 m(位移比为2.6%)，分块后计算的方向角α如表5所示, 分块结果如图10所示。

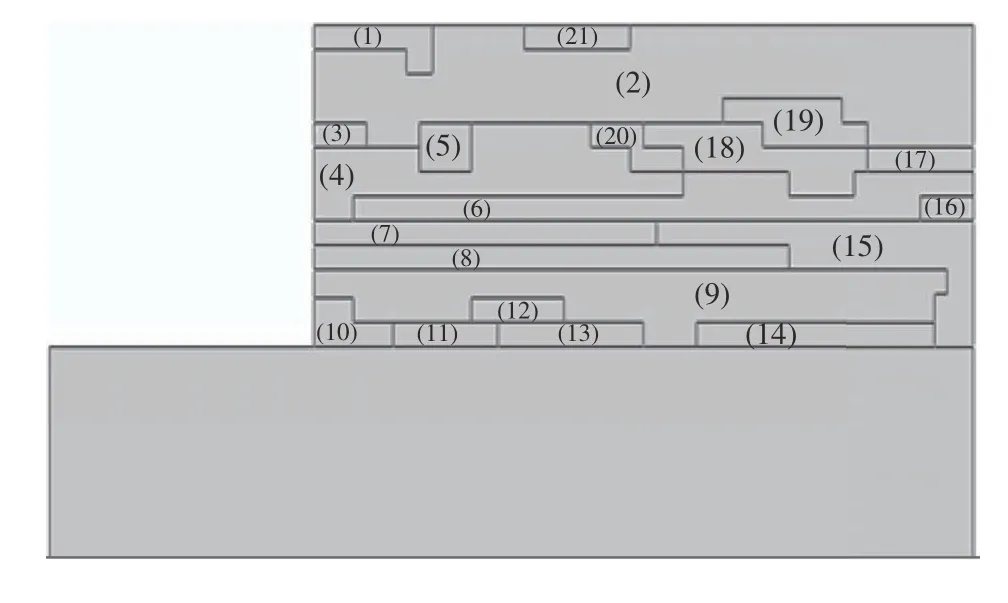
图10 分块图像Fig.10 Block image

3.4 计算结果小结

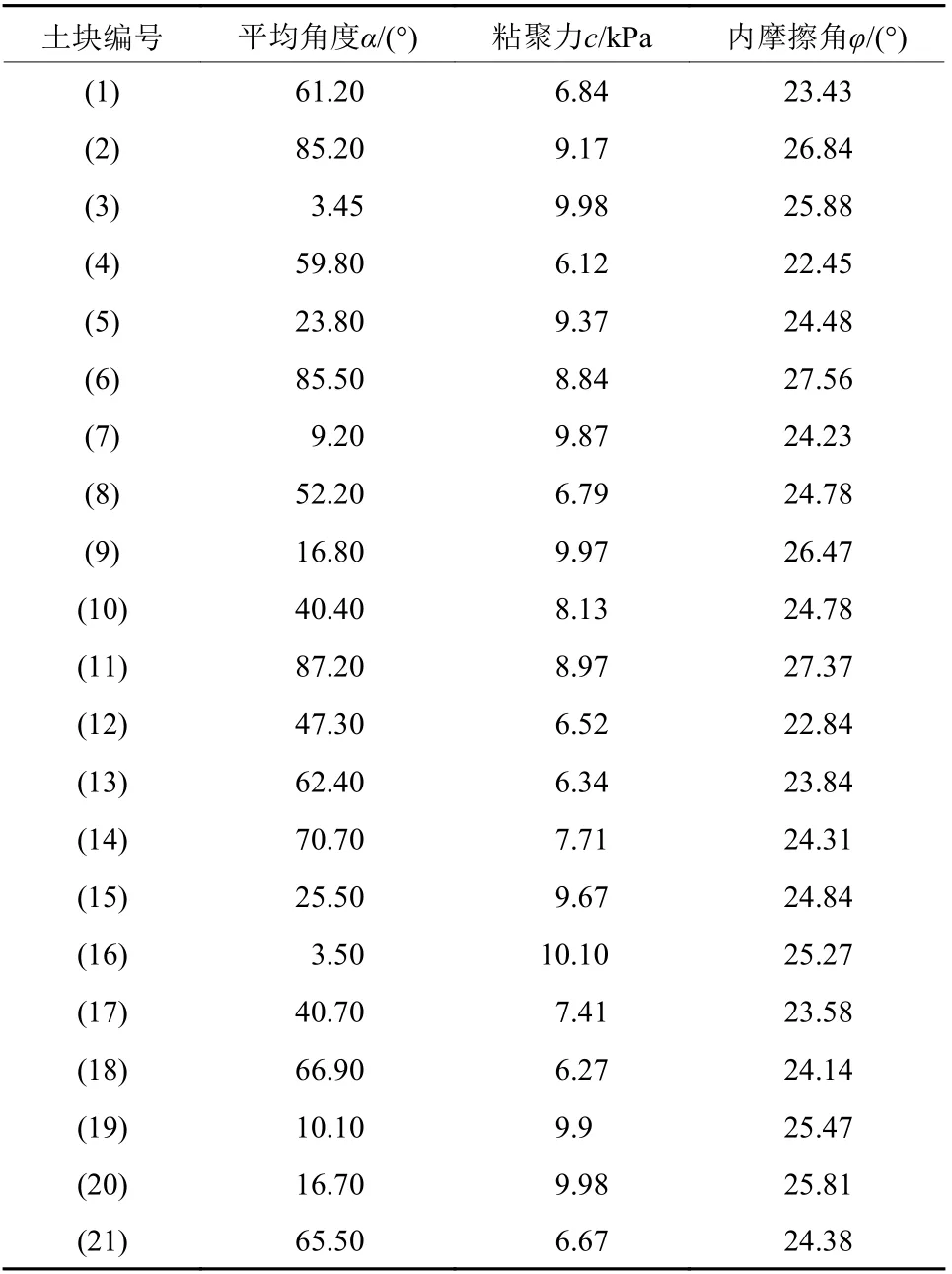
表5 分块强度参数Table 5 Block strength parameters

表6 横观各向同性与各向异性土压力比较Table 6 Comparison of anisotropic and isotropic earth pressures

将结果和朗肯土压力及库伦土压力作比较，可得出朗肯的理论解远远小于数值解，而库伦的理论解与多次位移后的各向异性解较为接近，这与徐日庆等[15]在刚性挡土墙模型试验得到T等位移压缩模式下被动土压力的结论一致。将3种情形汇总如图11所示，强度各向同性与一次位移的土压力变化情况类似，沿墙背先是接近直线分布，在快靠近墙踵部位压力值减小，与赵光辉等研究的土压力曲线类似[16]，原因是底部土体摩擦引起墙底部土压力值减小，而多次位移的被动土压力在墙背后2～3.2 m范围出现减小的原因是多次位移施加后在这一范围的强度主要受分块4来控制，而这块塑性区偏转的平均角度为59.8°，为强度最弱的区域，因此应力曲线并不会跟各向同性一样成直线增加而是出现局部减小的现象。

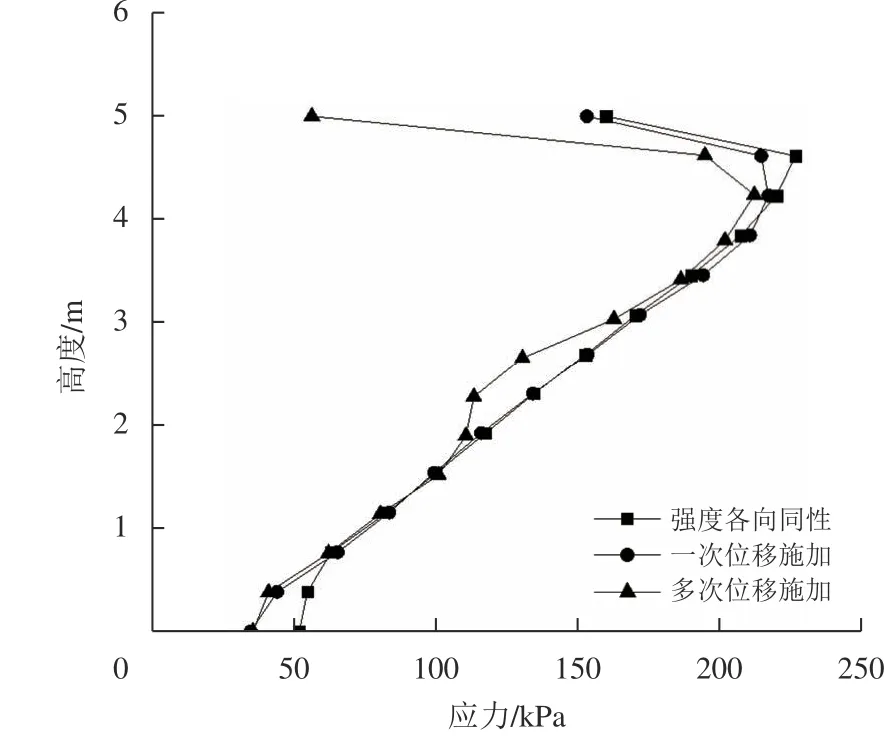
图11 土压力强度比较Fig.11 Comparison of soil pressure strengths

4 多种因素对各向异性显著性影响

4.1 α=30°对各向异性的影响

选用α=30°(即沉积面与水平面方向成30°),墙土间的接触面摩擦角δ=2φ/3，利用 ABAQUS可计算得到模型位移一次施加(墙体位移比为4%)后的结果如图12和表7所示。考虑与墙背光滑下的分块后的结果相类似，本文墙背粗糙位移一次施加的分块信息不再列出。

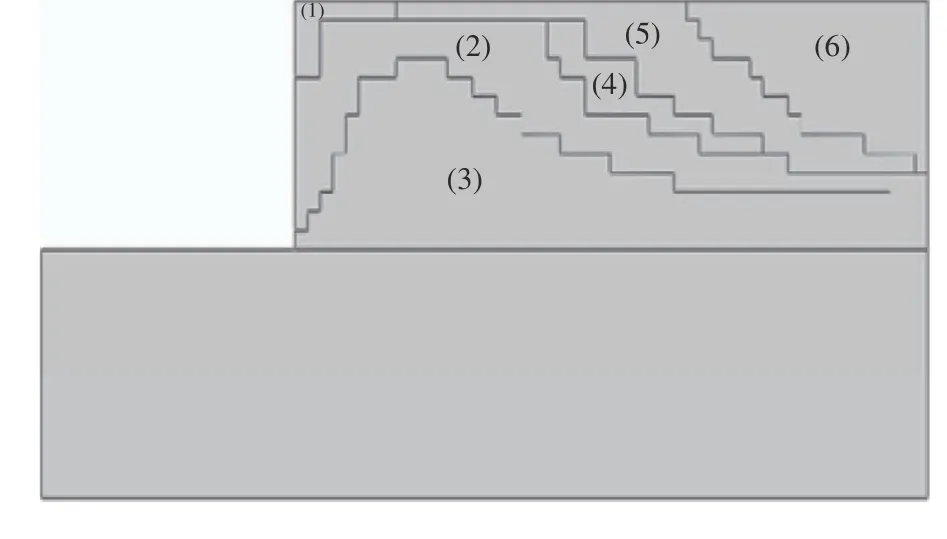
图12 分块图像Fig.12 Block image

4.2 多种因素对各向异性的影响比较

研究土体沉积面倾斜以及墙背粗糙对土体被动土压力的影响，结果如表8及图13所示。

表7 分块强度参数Table 7 Block strength parameters

表8 横观各向同性与各向异性土压力比较Table 8 Comparison of anisotropic and isotropic earth pressures

图13 土压力强度比较Fig.13 Comparison of soil pressure strengths

由图13和表8可知土体沉积面倾斜以及墙背粗糙皆对土体的被动土压力产生较大影响。

5 M-C，D-P4 ，M-N，L-D的计算结果

表9 各屈服准则之间的关联Table 9 Association between yield criteria

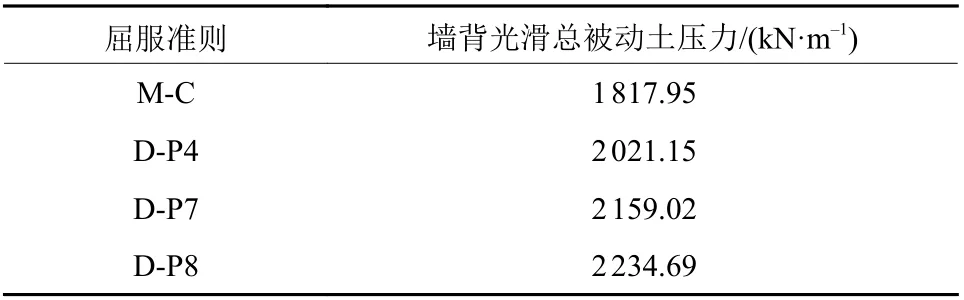
表10 各屈服准则被动土压力比较Table 10 Comparison of yield criterion and passive earth pressures

4种屈服准则下土体被动土压力强度大小，结果如图14所示。

从表10和图14的计算结果看，D-P4与D-P7的计算结果介于中间，且两者的值相近。从安全和经济角度，可取D-P4或D-P7的结果作为被动土压力的参考值。

6 结论

图14 各屈服准则下被动土压力Fig.14 Passive earth pressures under each yield criterion

为了探究土体内部真实应力场分布，在做被动土压力墙体平动研究时，对同一模型分一次位移施加和多次位移施加进行计算，结论如下：

(1)横观各向同性土体，多次位移比一次位移施加得到的总被动土压力要小，且随着施加位移次数增多越接近库伦土压力的理论解，一次位移施加产生的破裂面为平面，多次位移施加后产生的破裂面为曲面。但两者计算出的被动土压力差值较小。

(2)α=30°时对被动土压力的影响要比α=0°时的更为显著，这是因为α=30°时的塑性贯穿区域所在位置的大主应力偏转平均角度在42°～57°之间，而这一区间对应的强度参数最小，因此在这种情形下算得被动土压力会减小很多。

(3)4种强度准则下土压力的对比：D-P4(等面积圆)和Matsuoka-Nakai的结果介于Mohr-Coulomb与Lade-Duncan之间，D-P4的结果接近D-P7的，计算结果跟理论分析相符合，说明用ABAQUS计算被动土压力的合理性。

(4)考虑土体的横观各向同性对被动土压力的影响，另一方面考虑4种不同的强度准则对计算被动土压力的影响，便于对被动土压力的大小和范围有合理的了解，有利于挡墙的合理设计。