基于桩-土剪切特性的托底抗拔桩承载力分析
聂永江,邵光辉
(南京林业大学土木工程学院,南京 210037)
地下工程的抗浮问题事关工程的安全,若处理不当将会引发严重的后果。设置抗拔桩是基础抗浮设计的主要措施。托底抗拔桩是通过无黏结钢绞线将上拔力作用点转移至桩底,桩身混凝土受压工作的新型抗拔桩[1]。与普通抗拔桩相比,托底抗拔桩具有良好的桩身抗裂性能及承载能力。
赵晓光[2]现场实测发现托底抗拔桩从桩底由下至上的荷载传递方式,使得桩身下部侧阻力得到充分发挥,抗拔承载力在一定程度上得到提高。邵光辉等[1]通过模型试验讨论了托底抗拔桩与普通抗拔桩在荷载传递特性上的差异,提出了托底抗拔桩极限承载力的计算方法。现有的研究成果初步揭示了托底抗拔桩的变形和荷载传递机理,但是对于桩-土相互作用及其对桩抗拔承载力的影响尚缺乏系统深入的理论研究。陈杨等[3]对砂土地基中抗拔桩的研究发现,松砂与密砂中的抗拔桩的承载特性有显著差异,砂的相对密实度不仅影响抗拔桩的承载力,而且会影响桩侧摩阻力的分布形式。基于托底抗拔桩的受力特点,建立既反映桩周土体剪切特性又体现桩身轴力传递规律的承载力理论计算模型,对于丰富其设计理论,进一步推进工程应用具有重要意义。
考虑桩-土相互作用,载荷传递法是分析桩的荷载-位移特性的有效方法[4-5]。高文静等[6]提出了同时考虑桩侧、桩端弹性阶段、塑性阶段以及滑移阶段在内的统一三折线荷载传递模型,用于计算承压桩沉降变形。李兰勇[7]基于三折线侧阻软化模型推导出了普通抗拔桩的荷载-位移关系。吴跃东等[8]基于桩-土软化模型推导出了单桩荷载传递规律的解析解,并通过单桩静载荷试验发现,桩侧摩阻力的软化行为会引起桩承载能力的降低。由于托底抗拔桩与普通抗拔桩在桩-土界面剪切位移分布方面差异巨大,因此难以直接应用普通抗拔桩的理论获得托底抗拔桩的极限承载力。
本研究分别采用双折线、三折线荷载传递函数模拟桩侧松砂、密砂的剪切特性,探讨托底抗拔桩的极限承载力变化规律,分析其与普通抗拔桩之间的差异,提出单桩荷载-位移的算法及解答,为托底抗拔桩的设计提供理论参考。
1 荷载传递函数
天然土层是漫长而复杂的地质作用的产物[9],不同类型的土体有各自的工程特性。在砂土地基中,混凝土桩与桩周土体接触面的应力-应变特性与砂土的密实程度紧密相关。对于松砂地基,桩-土接触面的剪应力-剪切位移曲线呈现应变硬化的特征[10],即当剪切位移较小时,剪切力随剪切位移快速增加;当剪切位移达到一定值时,剪切力趋于稳定,并不再随剪切位移增加而显著变化。对于密砂地基,桩-土接触面的剪应力-剪切位移曲线呈现应变软化的特征,有明显的峰值,峰值后应力随变形增大而降低,最后达到残余强度[11]。
当桩周为松砂时,桩-土接触面剪切荷载传递函数如图1a所示,用双折线模型表示为:
(1)
式中:τ为桩-土剪应力;s为桩-土剪切位移;λ为桩侧土的抗剪刚度系数;τu为桩侧土的抗剪强度;su为弹性和滑移的界限位移。
当桩周为密砂时,桩-土接触面剪切荷载传递函数如图1b所示,用剪切软化三折线模型[12]表示为:
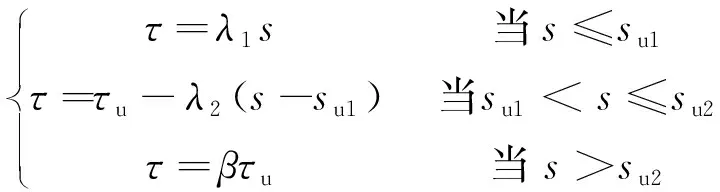
(2)
式中:λ1为桩侧土弹性阶段的抗剪刚度系数;τu为桩侧土的抗剪强度;su1为弹性和软化的界限位移;su2为软化和滑移的界限位移;λ2为桩侧土软化阶段的抗剪刚度系数;β为软化系数。

图1 荷载传递函数曲线Fig. 1 Curves of load transfer functions
桩侧砂土的抗剪强度随深度线性增加:
τu=fz
(3)
式中:f为抗剪强度增长系数,可取K0γ′tanφ,K0为静止侧压力系数,γ′为砂土有效重度,φ为砂土内摩擦角;z为计算点埋深。
2 托底抗拔桩受力性状分析
托底抗拔桩的结构示意图见图2。桩底锚具将无黏结钢绞线锚固于桩底,通过无黏结钢绞线将基础底板处的上拔力传递至桩底。在上拔荷载作用下,桩身混凝土受压工作。
为简化计算,分析时不考虑桩身自重应力沿深度变化的影响。深度z处的桩侧摩阻力τ和桩身位移s之间满足荷载传递微分方程[12]:
(4)
式中:A和Ep分别为桩身横截面积和弹性模量;U为桩身横截面周长。
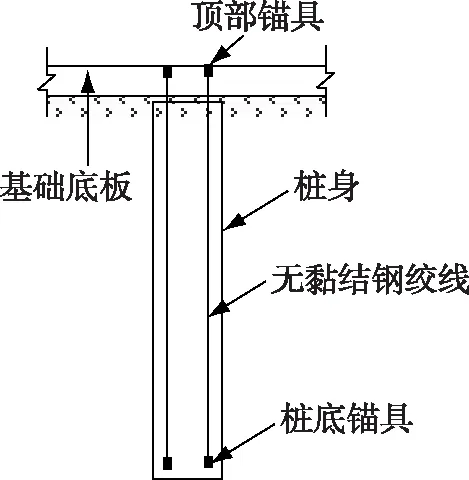
图2 托底抗拔桩的结构示意图Fig. 2 Structural schematic diagram of bottom uplift pile
2.1 松砂中托底抗拔桩的受力分析
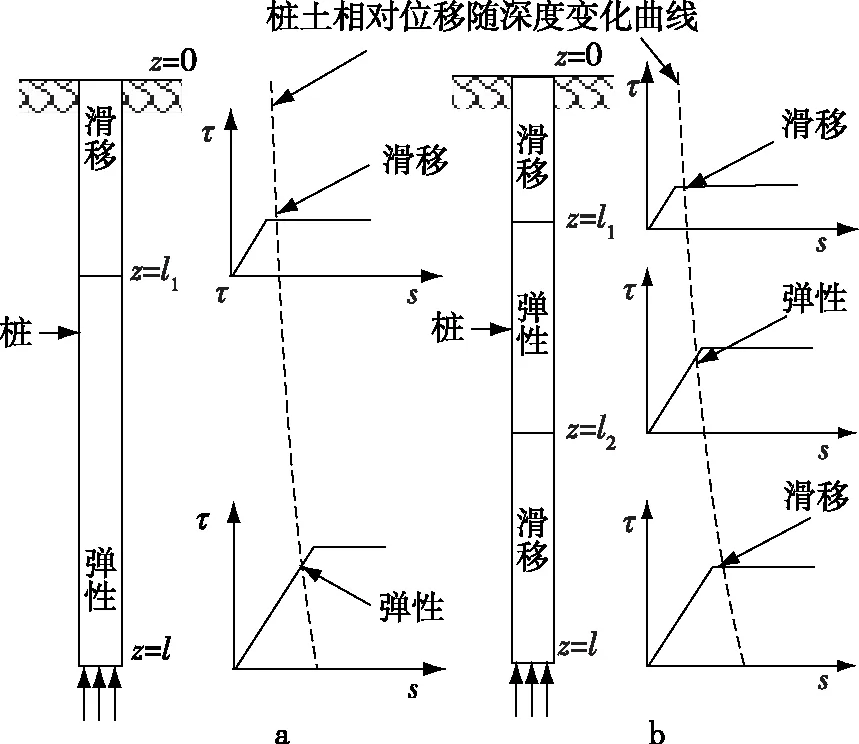
图3 松砂中桩-土界面剪切状态分布Fig. 3 Distribution of shearing state of pile-soil interface in the loose sand ground
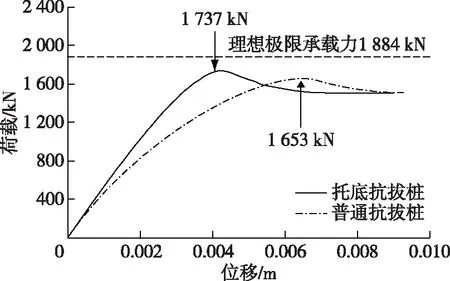
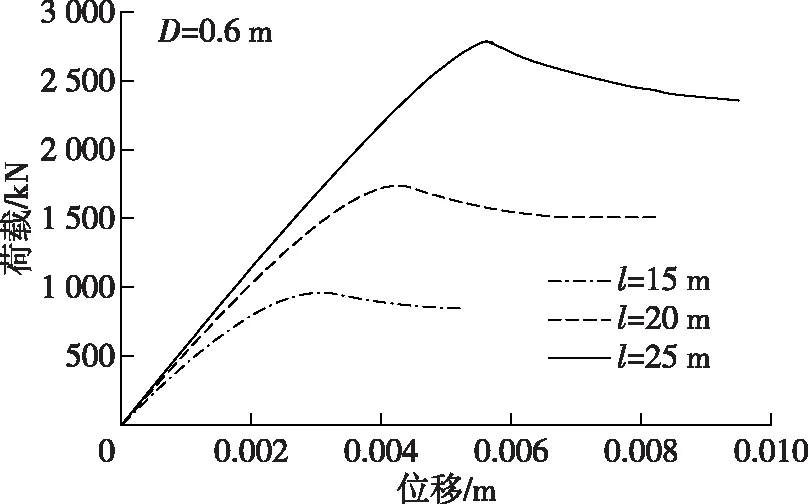
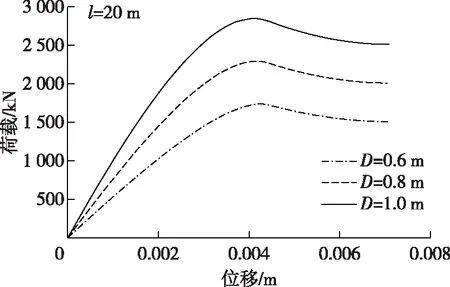
已有研究表明[13],托底抗拔桩的桩-土位移沿深度非线性变化。而桩周砂土受自重应力作用,抗剪强度随深度线性变化。因此,桩-土剪切应力并不会同步达到抗剪强度峰值。当上拔荷载较小时,桩-土剪切位移s (5) 考虑泊松效应影响[1],托底抗拔桩的承载力为: (6) 式中:η为桩的相对柔度参数[1],η=νptanδ(l/D)(Gavg/EP),l、D、νp和Ep分别为桩长、桩径、桩的泊松比和弹性模量;Gavg为桩侧土的平均剪切模量。 由于密砂的应变软化特性,不同深度处桩-土剪切界面峰值强度对应的剪切位移与桩-土的实际位移不同步。托底抗拔桩受荷载较小时,桩下部的桩-土位移s 图4 密砂中桩-土界面剪切状态分布Fig. 4 Distribution of shearing state of pile-soil interface in the dense sand ground 0~l1段桩-土体系处于滑移阶段,桩身侧摩阻力均达到残余强度,故该段的桩侧摩阻力为: τ=βfz (7) 在z=l1处即滑移段与软化段分界处位移和轴力分别为: (8a) (8b) l1~l2段桩-土体系处于软化阶段,该段的桩侧摩阻力: (9) 将式(9)代入式(4)可得到软化段的位移和轴力: (10a) 式中: (11) 将式(8a)、(8b)作为边界条件代入式(10a)、(10b)中解得C1、C2。 在z=l2处即软化段与弹性段的分界处位移为: (12) 求解方程(12)可得到l2的两个解,取小值作为l2。由此可得在深度z=l2截面处的位移以及轴力: (13a) Ql2= (13b) l2~l段桩-土体系处于线弹性阶段,侧摩阻力与位移成正比,即: τ=λ1s (14) 结合式(4)得到弹性段的位移及轴力: s=C3eγ1z+C4e-γ1z (15a) Q=AEPγ1[C3eγ1z-C4e-γ1z] (15b) (16) 将式(13a)、(13b)作为边界条件代入式(15a)、(15b)中解得C3、C4。由此可以得到桩底的位移和上拔荷载: sl=C3eγ1l+C4e-γ1l (17a) Ql=AEPγ1[C3eγ1l-C4e-γ1l] (17b) 随着桩底位移的增加,桩侧摩阻力的变化经历以下两个过程: 1)桩-土体系弹性段的长度逐渐缩小,桩下部桩-土体系处于软化状态,随着位移的进一步增大,桩下部将出现滑移段并逐渐向上扩展,最终发展为整桩的桩-土体系处于滑移状态。在这一过程中,桩底荷载在第一阶段就已达到峰值,利用式(17a)、(17b)绘出Q-s曲线得到桩的极限抗拔承载力。 2)桩底荷载增加过程中,当桩底的桩-土位移s>su1时,靠近桩底的部分桩-土体系将出现软化区,此时桩侧摩阻力自上而下处于滑移-软化-弹性-软化的状态,如图4b所示,桩底位移的继续增大将导致软化区长度的增加,直至弹性段完全消失,弹性段的桩侧摩阻力充分发挥,桩底荷载达到峰值。仿照方程(12)的求解方法得到桩下部弹性段与软化段分界面的深度l3,继而可以求得该界面上的位移和轴力,再将该截面的位移和轴力作为边界条件,求得常数C5、C6,得到下部软化区位移和荷载的解析解: (18a) Ql= (18b) 绘出Q-s曲线得到桩的极限抗拔承载力。 随着桩底位移的继续增加,桩的中间软化段也逐渐减小直至消失,此时整桩的桩-土体系处于滑移状态。随着位移的增加,承载力不再增加。 剪切软化三折线模型涉及的参数主要有桩侧土弹性阶段和软化阶段的剪切刚度系数λ1和λ2、软化系数β以及抗剪强度增长系数f。 参数λ1可根据Randolph的剪切位移法[13],得出λ1的近似理论解: (19) 可得: (20) 式中:G为桩周土的初始剪切模量,不考虑其随计算深度的变化情况;r为桩身半径;ζ=ln (rm/r),rm=2.5l(1-vs),vs为土的泊松比。 为简化计算,令λ2=1/3λ1,软化系数β是桩侧阻的残余强度与峰值强度之比,根据现有成果,一般对打入桩β取0.5~0.8[14],对钻孔灌注桩β取0.9[15]。 根据文献[13]的工程案例,密砂地基中一单桩,桩身及土质参数如下:桩长l=20 m,桩径D=0.6 m,桩身弹性模量Ep=32 GPa,λ1=22 560 kPa/m,λ2=7 520 kPa/m,f=5 kPa/m,β=0.8。 计算得到的Q-s曲线如图5所示。托底抗拔桩达到极限承载力时所需要的位移远低于普通抗拔桩,主要是由于托底抗拔桩的下部极限侧摩阻力比传统抗拔桩提前发挥,这也反映在Q-s曲线的斜率上,托底抗拔桩的桩-土体系的刚度大于普通抗拔桩,这与赵晓光等[16]的试桩试验结果一致;相同的土层条件下,托底抗拔桩的极限承载力比普通抗拔桩极限承载力高。本算例中托底抗拔桩比普通抗拔桩极限承载力高6%,而且软化系数β越小,承载力差异越大。抗拔桩的理想极限承载力计算值见图5,即不同深度出桩-土剪切应力同时达到峰值强度对应的承载力,这也是目前传统桩基理论的计算方法。对比可见,同时考虑密砂的剪切软化特性与抗拔桩的桩体变形特性,由于桩侧极限摩阻力发挥不同步,无论是托底抗拔桩,还是普通抗拔桩,极限承载力都明显低于理想极限承载力理论计算值。因此在抗拔桩设计时应充分考虑到桩周土层的软化特性,以确保承载力取值安全可靠。 图5 托底抗拔桩与普通抗拔桩的Q-s曲线Fig. 5 Q-s curves of bottom uplift piles and traditional uplift piles 桩长和桩径对托底抗拔桩Q-s曲线的影响见图6和图7。可以发现,随着桩长的增加,托底抗拔桩的极限承载力和极限位移都明显增加,这主要是因为托底抗拔桩的上拔荷载作用点位于桩底,桩下部的上拔位移大于桩上部,更能有效地发挥桩下部的摩阻力。增加桩长虽能提高单桩极限承载力,但是上拔位移也会显著增大。通过增大桩径的方式提高单桩极限承载力,不会改变极限位移。在上拔变形受控的情况下,增加桩径是提高托底抗拔桩极限承载力的有效方法。 图6 不同桩长托底抗拔桩的Q-s曲线Fig. 6 Q-s curves of bottom uplift piles with different lengths 图7 不同桩径托底抗拔桩的Q-s曲线Fig. 7 Q-s curves of bottom uplift piles with different diameters 软化系数β反映了砂土剪切软化后由峰值强度到残余强度的衰减程度,β值越大,强度衰减越小,软化越不明显。在算例中以软化系数β为变量,其他参数不变,分析极限承载力的变化情况。从图8可以看出,随着β值的增大,托底抗拔桩的极限承载力在不断提高,而软化越突出的土对应越低的β值,极限承载力越低。 图8 极限承载力与软化系数的关系Fig. 8 Relationship of ultimate bearing capacity and softening coefficient of bottom uplift pile 综上所述,虽然托底抗拔桩的极限承载力高于普通抗拔桩,但是由于托底抗拔桩的上拔荷载作用点位于桩底,桩-土相对位移下部大、上部小,当桩周土体为具有剪切软化特性的密砂时,不同深度处的桩侧峰值摩阻力不能同步达到,导致极限承载力比传统理论计算值低。因此,在托底抗拔桩设计时应充分考虑桩周土层的剪切特性,尤其对于软化系数低的密实砂土更应关注。本研究基于单桩分析获得了托底抗拔桩的承载力变化规律,对于相邻或群桩等存在桩间相互影响的情况,尚需根据具体的工况条件作进一步研究。 基于不同密实程度砂土的荷载传递函数,在分析桩-土体系剪切状态发展过程的基础上,推导了托底抗拔桩荷载-位移的解析解,通过工程算例讨论了托底抗拔桩的极限承载力及其影响因素。得到以下结论: 1)松砂地基中托底抗拔桩在达到极限破坏时,桩-土剪切应力能够全部达到极限强度,极限承载力可以按照桩-土体系的峰值抗剪强度计算。 2)密砂地基中托底抗拔桩极限承载力计算应考虑桩周土层的剪切软化特性,托底抗拔桩在达到极限破坏时,不同深度处桩-土剪切应力不能同步达到极限强度,极限承载力低于传统理论计算值。 3)密砂地基中托底抗拔桩的极限承载力明显高于普通抗拔桩,且达到极限承载力时托底抗拔桩发生的位移变形远小于普通抗拔桩。 4)软化系数是影响托底抗拔桩极限承载力的重要因素,软化系数越低,托底抗拔桩的极限承载力越低,与传统理论计算值相差越大。2.2 密砂中托底抗拔桩的受力分析
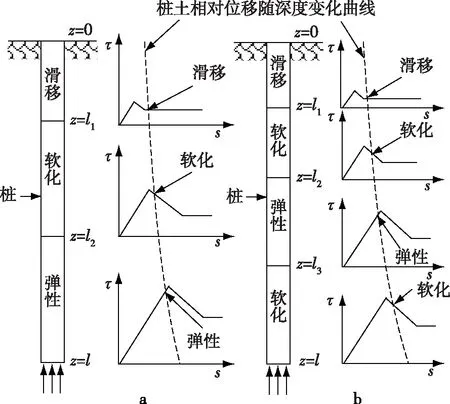
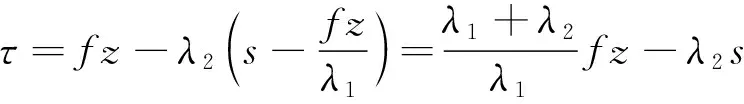
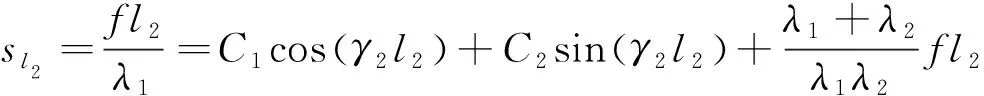
3 参数确定
4 工程算例及参数敏感性分析

5 结 论

