平动点周期轨道间小推力转移的Gauss伪谱法

周敬，胡军，*

1. 北京控制工程研究所，北京 100190 2. 空间智能控制技术重点实验室，北京 100094

近年来，随着航天基础理论的不断深入研究和工程实践技术的快速发展，深空探测越来越受到世界各航天大国与组织的重视。根据中国航天事业发展的指南，未来航天的三个重点方向之一就是深空探测[1]。相比以经典摄动二体运动问题为基础的近地空间航天活动，深空探测所涉及的运动模型更多的是三体问题。动力学本质上的区别使得三体问题相对二体问题更加复杂。在三体问题的研究中，平动点(尤其是共线平动点)及其附近的周期/拟周期轨道所具有的独特位置优势和丰富的动力学特性[2]，使其在深空探测任务设计中占据着重要的地位，已经成为宇宙观测、天文研究的理想场所和星际高速公路(interplanetary superhighway，IPS)的门户站。

通常情况下，在平动点轨道进入工程应用之前，首先需要解决的便是与其有关的轨道转移问题。按照推进方式的不同，平动点轨道之间的转移可以分为脉冲转移和小推力转移两种方式，且小推力转移已逐渐成为深空探测领域的研究热点。

在小推力轨道转移方面，小推力推进系统具有比冲高、推力小、工作时间长、推进剂消耗量少等特点，非常契合深空探测的任务特点，在深空探测研究中具有广阔的应用前景。然而，小推力的引入不可避免地使原本就复杂的三体问题的复杂性进一步增加，导致相关的轨道设计与优化面临新的问题与挑战。目前，小推力轨道优化方法主要分为直接法、间接法和混合法[3-4]。直接法虽然收敛性较好，但求解精度较低，计算量大，对于小推力轨道优化这类非线性、多局部极值问题，解的最优性一般难以保证。间接法虽然可以保证解的最优性，但协态变量无明确物理意义，难以给出合理的初始猜测值。混合法兼顾间接法和直接法的优点，精度更高、收敛域更宽、数值稳定性更好，但同时复杂性也更大。

在小推力研究方面，文献[5]借助平动点轨道的相空间结构揭示了小推力转移的机理，对小推力方式的地月低能转移问题进行了研究。文献[6]采用遗传/逐次二次规划混合优化算法，研究了近地小推力转移轨道的制导问题。文献[7]基于轨道逆推思想，采用人工免疫算法对地月转移轨道设计中的小推力捕获轨道进行求解。文献[8]提出了基于N次逆多项式逼近的半解析Lambert算法，并基于该算法发展了一种转移轨道初始设计方法，实现了行星际小推力轨道设计。文献[9]结合小推力技术和金星借力技术，研究了火星转移轨道设计问题。文献[10]结合小推力技术和bang-bang控制技术，研究了高精度的皮纳卫星编队构型保持问题。

Gauss伪谱法是近年来新兴的一种高效的最优控制问题求解方法，本质上属于直接法，其具有三个显著优点：1)动力学约束只与当前节点状态有关，寻优参数规模小；2)KKT(Karush-Kuhn-Tucher)条件与极大值原理中的一阶最优性条件等价，求解精度高；3)具有伪谱法共有的指数收敛特性，收敛性好。目前有关Gauss法的研究主要有：杨博等利用Gauss伪谱法研究了地球同步轨道卫星轨道转移问题[11]；曹喜滨等基于Gauss伪谱法将最优控制问题离散化为NLP问题，并采用基于逆多项式的形状法给出了NLP初值的计算方法[12]；尚海滨等基于Gauss伪谱法的配点特性，推导出了性能指标和约束方程的解析雅可比矩阵，进而解决了星际小推力转移轨道优化问题[13]。

由于Gauss伪谱法得到的NLP模型包含较多的等式约束，且小推力轨道的非线性较强，控制变量初值设置的不合理往往会导致NLP的求解迭代时间长、容易陷入局部极小甚至不收敛等问题，因此对Gauss伪谱法的控制变量初值确定方法进行研究具有重要意义。目前，对初值确定方法研究最多的是形状法，主要有：文献[14-16]采用逆多项式函数作为小推力转移轨道的形状函数，对小推力轨道转移问题进行研究；Ellutini等利用正弦指数函数作为形状函数，来近似小推力转移轨道[17]；Novak等提出了一种基于伪春分轨道根数的三维形状方法[18]，解决了地球-火星转移轨道设计；Gondelach等提出了速度速率图的概念，将小推力轨道转移的速度矢量表示为时间或者极角的形状函数，然后对此函数进行优化，实现了地球-火星、小行星、彗星和水星之间的转移[19]；文献[20-22]利用Fourier级数作为小推力转移轨道的形状函数，对小推力轨道转移问题进行了研究。

上述研究均获得了不错的研究成果，但基本都是针对传统常见的轨道转移问题。对于平动点周期轨道间的小推力转移这一新兴问题，国内外研究很少涉及，且三体问题相对二体问题的复杂性可能使得上述研究方法无法适用于平动点轨道之间的小推力转移问题。鉴于小推力技术在深空探测中具有的广泛应用前景，本文在充分研究三体问题特性的基础上，构造了一种新的形状函数，并在此基础上基于Gauss伪谱法对共线平动点周期轨道间的小推力转移进行了研究，以期为未来中国深空探测事业以及平动点轨道工程应用奠定一定的理论基础。

1 轨道转移优化模型

1.1 动力学模型

在三体问题中，圆型限制性三体问题(circular restricted three-body problem, CRTBP)是最简单的三体运动模型，常用来研究最基本的运动规律，同时考虑到地月L1点作为地球通向宇宙空间的门户站以及在此部署空间站的可能性，具有重要的工程应用价值。因此本文以地月系统CRTBP下的L1点附近的周期轨道作为本文的研究对象。

为方便描述航天器运动和简化计算，在CRTBP中通常需要对相关物理量进行无量纲化处理，并以时间作为独立变量。相应的质量[M]、长度[L]和时间[T]的归一化单位取为：

(1)

式中:m1和m2为两主天体质量；L12为两主天体之间的距离；G为万有引力常数，其他相关变量的归一化过程均可依据式(1)推导获得。

为了更直观、更清晰地描述航天器在CRTBP中的运动，通常选择在会合坐标系(也称为质心旋转坐标系)下进行研究。如图1所示，会合坐标系O-XYZ的原点位于两主天体的公共质心，x轴由较大主天体指向较小主天体，z轴与主天体系统角动量方向平行，y轴满足右手坐标系定则。

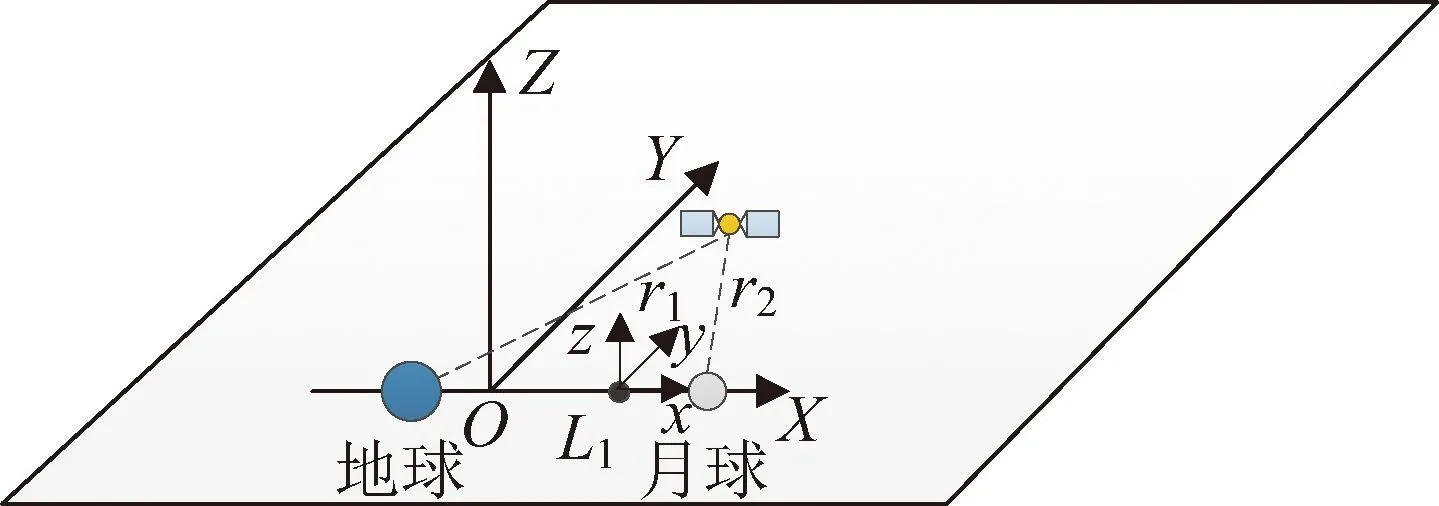
图1 地月系统CRTBP下的会合坐标系O-XYZ和 L1会合坐标系L1-xyzFig.1 Synodic coordinate system O-XYZand L1-centered synodic coordinate system L1-xyz for CRTBP of Earth-Moon system

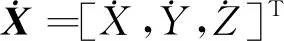
式中：F=[Fx,Fy,Fz]T为归一化后的推力加速度矢量及三轴分量；Ω为伪势能函数。

式中：X1为会合坐标系下L1点距离主天体公共质心的距离；γ1为L1点与最近主天体之间的距离。

因此，L1会合坐标系下航天器运动的动力学方程为：

(2)

(3)

此外，考虑到Halo轨道是共线平动点附近一类特殊的三维周期轨道，且常作为深空探测航天器的工作轨道，具有重要的学术研究和工程应用价值，Richardson基于Lindstedt-Poincaré方法推导了Halo轨道的三阶近似解析解，如下式所示，相关参数的含义及计算过程可以参考文献[23]。本文以Halo 轨道间的转移为例对小推力轨道转移进行研究。

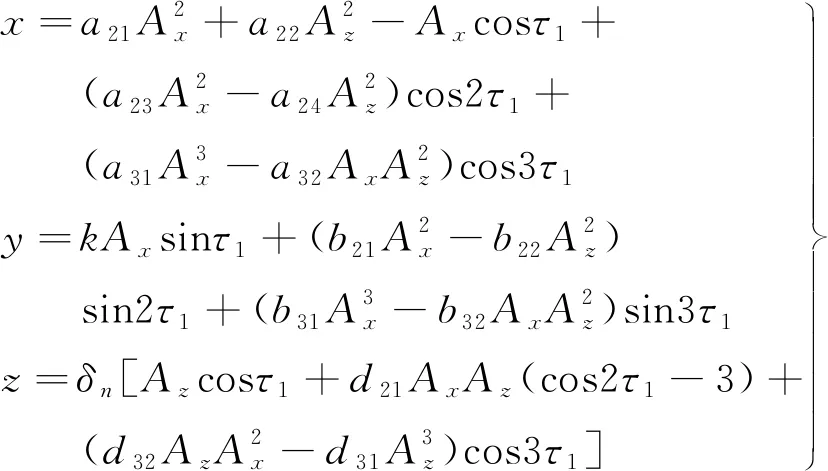
(4)

1.2 优化性能指标和约束

1)参考实际工程应用要求，优化性能指标按照燃料最优原则，即性能指标函数J取为:

式中：t0为轨道转移初始时刻，通常设置为零；tf为轨道转移结束时刻，通常根据任务需求给出取值范围；mfuel为轨道转移过程中的燃料消耗量；m0为航天器总质量；Tall=‖u‖2为飞行器总的推力加速度大小；g0为海平面重力加速度；Isp为发动机比冲。

2)考虑到发动机的最大推力限制，需要对推力加速度大小进行限制，归一化后的约束如下:

‖u‖2≤2DU

式中：DU为无量纲单位(dimensionless unit, DU)。

2 基于Gauss伪谱法的最优轨道 转移

2.1 轨道转移近似解析解

对于Gauss伪谱法下的小推力轨道转移优化设计，控制变量的初值选取对轨道优化设计的迭代过程具有非常重要的影响。为获得较快的收敛速度，合理的初始猜测值十分必要。本文在充分结合平动点附近轨道运动特性的基础上，构造了一种新的、专门适用于平动点周期轨道间转移的形状函数，下面进行详细介绍。

假设在L1会合坐标系下，小推力轨道转移的起点状态为x0，终点状态为xf，即

根据文献[23]，共线平动点附近运动的近似解析解为：

根据上式，要形成周期轨道，必然使得指数运动项A1eλ1t和A2e-λ1t为零，仅保留周期运动项，即A1=0,A2=0,Ax≠0,Az≠0，由此便得到了共线平动点附近周期轨道的一阶近似解析解，如式(5)所示，这也是本文提出的新的形状函数的原始形式。

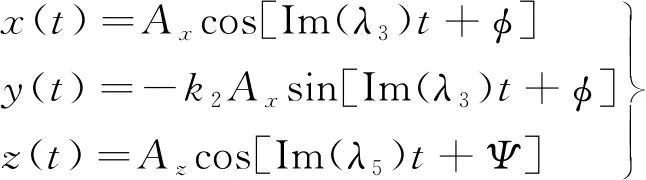
(5)

进一步，考虑到通常情况下小推力转移轨道的形状为螺旋状，如图2所示，对于这种轨道转移规律，Xie等和Ellutini等分别提出了经典的正弦指数函数[16]和逆多项式函数来近似小推力转移轨道[17]。对于CRTBP，参考共线平动点附近周期轨道的动力学特性，即式(5)，同时考虑小推力转移轨道的螺旋特性，在周期轨道近似解析解(5)的基础上，对振幅和相位进行时变处理，类似于轨道研究中常用的常数变易法，以此来构造一类新的形状函数来拟合小推力转移轨道。借鉴逆多项式形状函数思想，本文假设小推力转移轨道近似解析解的振幅和相位均按多项式变化，当然也可以假设其他形式的变化规律，如指数变化等，只要使得小推力转移轨道近似解析解满足螺旋特性即可。

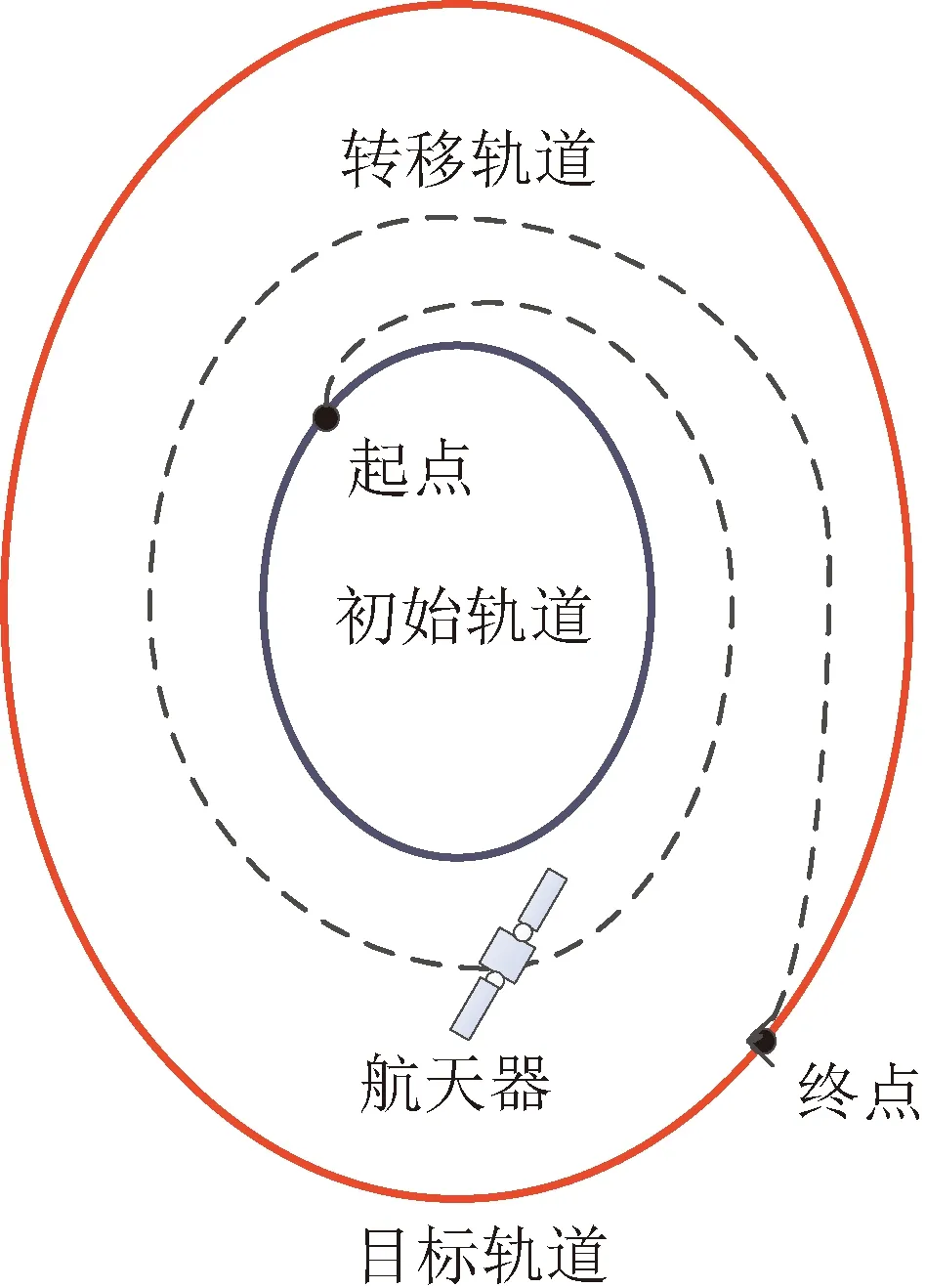
图2 小推力转移轨道示意Fig. 2 Sketch map of low-thrust orbit transfer

然后考虑轨道转移中的过程约束，如推力加速度大小约束等，便可获得其他约束方程，也可以通过试凑法配合事后验证的方法对多项式系数进行确定，最后获得满足约束条件的小推力转移轨道的近似解析解。

(6)

速度矢量表达式为：

(7)

加速度矢量表达式为：

(8)

(9)

将初始轨道和目标轨道的x轴振幅Ax1,Ax2和z轴振幅Az1,Az2，以及转移起点和终点在xy平面运动的相位φ1,φ2和z平面运动的相位Ψ1,Ψ2代入式(9)，便可以获得小推力转移轨道的近似解析解。这便是本文提出的一种新的、能够深度结合平动点周期轨道运动特性的形状函数法。

此外，由于式(5)作为平动点附近周期轨道的通用一阶近似解析解，不仅可以表示Halo轨道，还可以表示Lissajous轨道以及Lyapunov轨道等。因此，本文提出的形状法不仅适用于Halo轨道之间的转移，也适用于Lissajous轨道和Lyapunov轨道以及上述三种轨道相互间的转移。

2.2 Gauss伪谱法的离散化方法

Gauss伪谱法的主要思想是采用Lagrange插值和Gauss求积公式将最优控制问题在一系列Legendre-Gauss(LG)点进行离散化处理。参照文献[12]，由于LG点的取值区间为(-1,1)，因此需要对最优控制问题的时间区间进行线性变换，新的时间变量记为τ，变换方法如下：

进行上述变换后，本文所研究的最优控制问题将转化为如下形式，性能指标函数J为：

满足约束条件：

(1)约束方程离散化

Gauss伪谱法对于状态变量和控制变量的逼近通过全局Lagrange插值实现。假设离散化的LG点的个数为K，则采用初始状态变量x(τ0)和K个离散节点处的状态x(τi)=X(τi)，可得到K+1阶Lagrange插值多项式，利用该多项式对系统的状态变量进行近似：

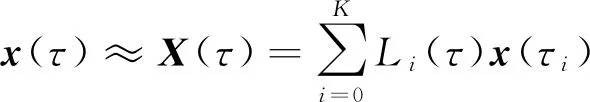
(10)

式中：X(τ)为Lagrange插值多项式；Li(τ)为Lagrange插值基函数，其计算公式如下：

式中：g(τ)为以各插值节点为根的多项式，即

显然式(9)中满足x(τi)=X(τi)，对式(10)进行求导，得到状态变量在LG点的导数为：

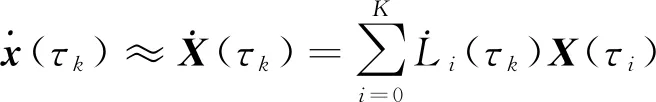
(11)

(12)

将式(12)代入式(11)，则微分形式的状态方程转化为以各个离散点表示的代数约束方程:

(13)

通过上式共得到K个等式约束，其中X(τk),U(τk)分别为离散点处的状态变量和控制变量，作为后续非线性规划的优化参数。

(2)末端约束离散化

在以上过程中，并未考虑末端状态约束，因此需要额外附加约束。采用Gauss求积公式对动力学方程进行积分：

则末端状态可形成如下代数约束：

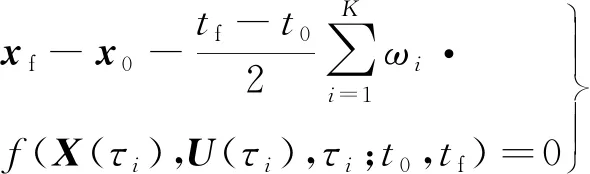
(14)

式中：ωi为Gauss求积系数，计算方式如下：

式中：P(τ)为n阶Legendre多项式。

(3)路径约束离散化

根据原始问题中控制变量的约束范围，将控

制变量的路径约束离散化为：

(15)

式中：k=1,…,K。

(4)目标函数离散化

采用Gauss求积公式近似式(6)中的积分项，则目标函数J可以离散化为：

(16)

至此，便实现了小推力转移轨道优化问题的离散化，即将最优控制问题转化为了NLP问题。根据Gauss伪谱法的求解过程，取如下非线性规划的变量作为优化变量：

Z={X1,…,XK,U1,…,UK,t1,tf}

(17)

式中：Xk和Uk分别为离散LG点处的六维状态变量和三维控制变量。

通过以上离散化方法，构成了以式(16)为性能指标，以式(17)中的参数为优化变量，以式(13)～(15)为约束方程的NLP问题。采用Gauss伪谱法的Matlab优化工具箱GPOPS对此NLP问题进行求解，并以形状法获得的控制加速度近似解作为初值，便可以获得要求的小推力转移轨道。

3 仿真分析

本节以地月CRTBP中L1点附近的Halo轨道作为研究对象，利用本文所提方法对Halo轨道之间的小推力轨道转移进行仿真研究。初始Halo轨道的振幅记为Ax1,Az1，目标Halo轨道的振幅记为Ax2,Az2，转移起点和终点的状态矢量分别记为x0,xf，以上参数的具体数值在L1会合坐标系下的取值如表1所示。

表1 Halo轨道间小推力轨道转移相关参数

首先采用形状法获得小推力转移轨道的近似解析解，在转移起点和终点的状态矢量x0,xf以及转移时间tf的范围确定之后，便可以根据式(6)～(9)获得小推力转移轨道的近似解析解，即获得了任意时刻的位置矢量、速度矢量以及控制加速度矢量的近似解，然后按照2.1节所述过程进行解算和处理，将获得的控制加速度矢量作为Gauss伪谱法的控制变量的初始猜测值，利用GPOPS优化工具箱对离散得到的NLP问题进行求解，最终获得最优小推力转移轨道。为满足不同的任务背景需求，下面分别针对不同转移时间的情形进行了研究。

3.1 转移时间较短

GPOPS无初始猜测值和有初始猜测值时的仿真结果如表2所示。由表2可以看出，在转移时间较短的情况下，在不同控制变量初始猜测值情况下，Gauss伪谱法获得了相同的最优性能指标0.7744和转移时间1.3818，说明不同控制变量初始猜测值不会对Gauss伪谱法的最终结果产生影响。然而，当形状法为Gauss伪谱法提供控制加速度的初始猜测值时，迭代次数由3469降至1558，降幅为55.1%，仿真时间由166.3s降至34.8s，降幅为79%，说明本文提出的形状法可以为Gauss伪谱法提供较好的初始猜测值，可以显著加快Gauss伪谱法的迭代过程。

表2 转移时间较短时不同初始猜测值下的 GPOPS仿真结果

图 3 转移时间较短时的小推力转移轨道Fig.3 Low-thrust transfer trajectories with short transfer time

图 4 转移时间较短时的三轴控制加速度Fig.4 Three-axis controlled acceleration with short transfer time

形状法和Gauss伪谱法下小推力转移轨道的轨道如图3所示，对应的三轴控制加速度的时间序列如图4所示。根据图3，采用形状法获得的小推力转移轨道与Gauss伪谱法优化得到的最优转移轨道基本一致，说明了本文提出的形状法的正确性。根据图4，Gauss伪谱法优化得到的最优推力加速度矢量与基于形状法获得的近似推力加速度矢量大体一致，且均满足推力加速度大小约束，进一步说明形状法具备为Gauss伪谱法提供合理初始猜测值的能力。

此外，形状法获得的加速度曲线比较光滑，而Gauss伪谱法获得的加速度曲线则有几处突变，说明形状法相比Gauss伪谱法，所求解的转移轨道具有更好的稳定性。

3.2 转移时间较长

在一定任务背景下，当需要进行较慢的轨道转移时，此时轨道转移时间较长，转移轨道可以形成多圈(即圈数N≥1)，以单圈为例，此时可以设置转移时间tf的取值范围为[T,2T]。根据3.1节所述方法，获得Gauss伪谱法下的最优小推力转移轨道。

GPOPS无初始猜测值和有初始猜测值时的仿真结果如表3所示。由表3可以看出，在转移时间较长，且控制变量初始猜测值不同的情况下，Gauss伪谱法获得了相同的最优性能指标0.8859和转移时间4.1444，同样说明不同控制变量初始猜测值不会对Gauss伪谱法的最终结果产生影响。同样地，当形状法为Gauss伪谱法提供控制加速度的初始猜测值时，迭代次数由3657降至1251，降幅为65.8%，仿真时间由171.5s降至30.7s，降幅为82.1%，说明本文提出的形状法可以为Gauss伪谱法提供较好的初始猜测值，可以显著加快Gauss伪谱法的迭代过程，并且转移时间越长，加速效果越显著。

转移时间较长时，形状法和Gauss伪谱法下小推力转移轨道的轨迹如图5所示，对应的三轴控制加速度的时间序列如图6所示。根据图5可知，采用形状法获得的小推力转移轨道与Gauss伪谱法优化得到的最优转移轨道基本一致，说明了本文所提出的形状法的正确性。根据图6可知，Gauss伪谱法优化得到的最优推力加速度矢量与基于形状法获得的推力加速度矢量基本一致，且均满足推力加速度大小约束，同样进一步说明了形状法具备为Gauss伪谱法提供合理的初始猜测值的能力。

同样，形状法获得的加速度曲线相比Gauss伪谱法依然较为光滑，反映到转移轨迹上，形状法转移轨迹变化平稳、且一直处于目标轨迹的边界内，而Gauss伪谱法转移轨迹变化略大、且有超出目标轨迹的边界，进一步说明形状法相比Gauss伪谱法，所求解的转移轨道具有更好的稳定性。

表3 转移时间较长时不同初始猜测值下的 GPOPS仿真结果

图5 转移时间较长时的小推力转移轨道Fig.5 Low-thrust transfer trajectories with long transfer time

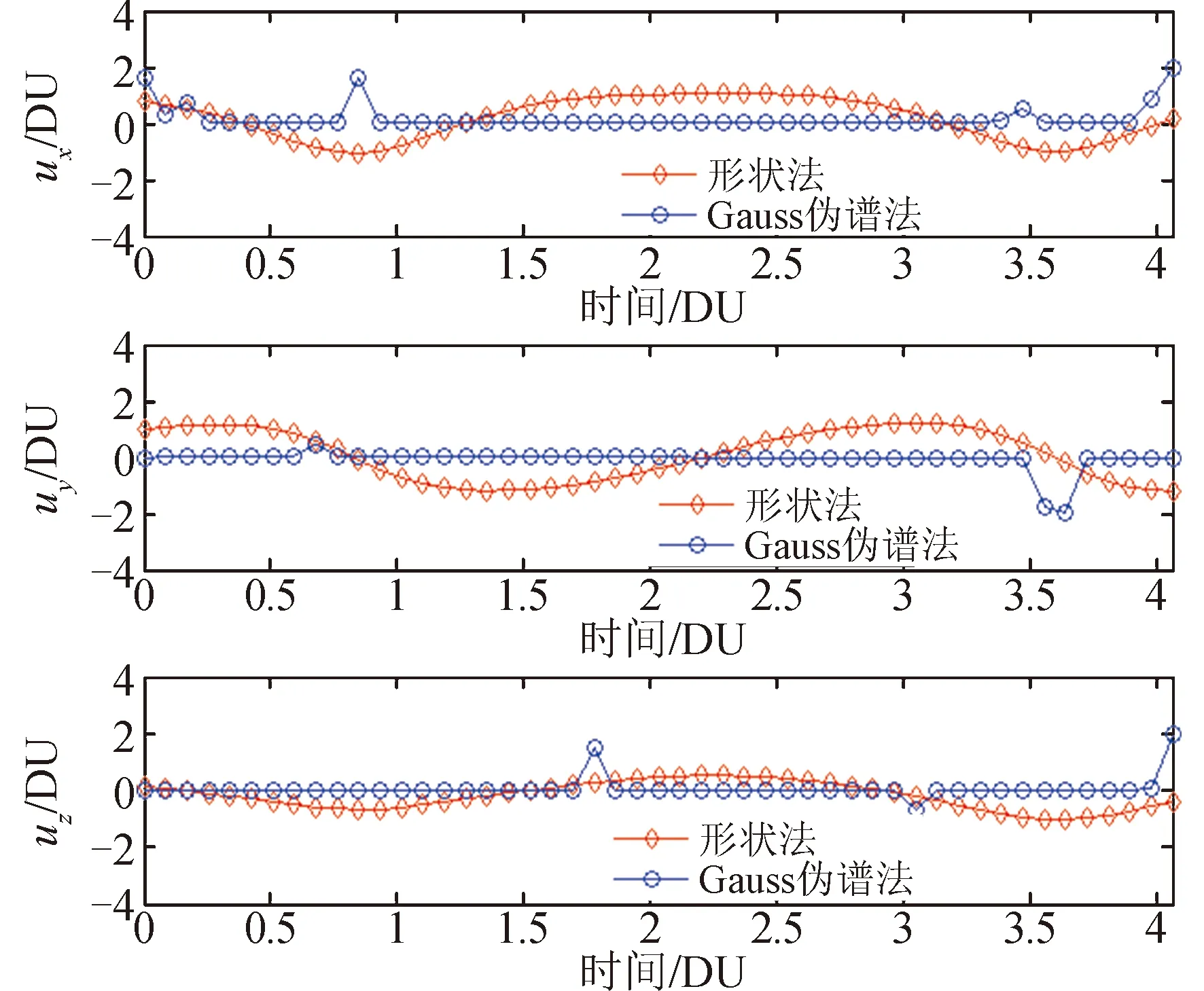
图6 转移时间较长时的三轴控制加速度Fig.6 Three-axis controlled acceleration with long transfer time

4 结束语

本文在深度研究平动点附近周期轨道特性的基础上构造了一种新的形状函数，并在此基础上提出了一种基于Gauss伪谱法的小推力轨道转移研究方法，解决了三体问题下共线平动点附近周期轨道间的小推力轨道转移问题。主要结论如下：

1)根据初始轨道和目标轨道的轨道类型，结合小推力转移轨道的螺旋特性和提出的振幅和相位按多项式变化的假设，获得的小推力转移轨道的近似解析解具备有效性和一定的普适性，可以为Gauss伪谱法提供较为有效的控制变量初始猜测值；

2)对小推力转移轨道的近似解析解进行解算和处理所获得的控制加速度估计值，作为Gauss伪谱法中控制变量的初始猜测值，可以显著提高Gauss伪谱法的迭代速度；

3)采用Gauss伪谱法将小推力轨道转移的最优控制问题离散化为NLP问题，并结合形状法提供的控制变量初始猜测值，可有效解决共线平动点附近周期轨道间的小推力轨道转移问题，同时也可为中国的深空探测事业和平动点轨道的工程应用奠定一定的理论基础。

本文提出的近似解析解的系数通过试凑法配合后期过程约束检验的方法确定，缺乏一定的理论指导，因此后续工作可以对过程约束指导下的近似解析解进行研究。