SYNCHRONIZATION OF COMPLEX NETWORKS VIA A SIMPLE AND ECONOMICAL FIXED-TIME CONTROLLER

LI Na,WU Xiao-Qun

(1.School of Mathematics and Statistics,Henan University,Kaifeng 475004,China)

(2.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)

1 Introduction and Main Results

Consider the following differential equation

where x∈Rndenotes the state variable of system(1.1),f:Rn→Rnis a nonlinear vector field and x0is the initial value of the system.

Definition 1.1[1]The origin of system(1.1)is said to be globally finite-time stable if for any of its solution x(t,x0),the following statements hold:

(i)Lyapunov stability:for anyε>0,there is aδ=δ(ε)>0 such thatkx(t,x0)k<εfor anykx0k≤δandt≥0.

(ii)Finite-time convergence:there exists a functionT:Rn{0}→(0,+∞),called the settling time function,such that limt→T(x0)x(t,x0)=0 and x(t,x0)≡0 for allt≥T(x0).

Definition 1.2[2]The origin of system(1.1)is said to be fixed-time stable if it is globally finite-time stable and the settling time functionT(x0)is bounded for any x0∈Rn,i.e.,there existsTmaxsuch thatT(x0)≤Tmaxfor all x0∈Rn.

Lemma 1.3[2]If there exists a continuous,positive definite and radically unbounded functionV(x(t)):Rn→R such that any solution x(t)of system(1.1)satisfies the inequality

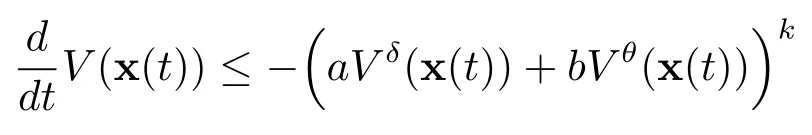
fora,b,δ,θ,k>0 andδk>1,θk<1,then the origin of system(1.1)is fixed-time stable,and the settling timeT(x0)is upper bounded and satisfies

Lemma 1.4If there exists a continuous,positive definite and radically unbounded functionV(x(t)):Rn→R such that any solution x(t)of system(1.1)satisfies the inequality

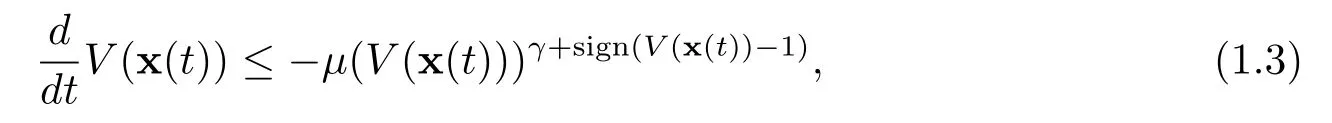
in whichµ>0,1≤γ<2,then the origin of system(1.1)is globally fixed-time stable.In addition,for any initial state x0of system(1.1),the settling time is described as

Remark 1There have been plentiful literature investigating fixed-time synchronization in recent years.Lemma 1.3 is the most common one to prove synchronization within a settling time[2]–[3].However,the special case ofk=1 in lemma 1.3 is commonly applied to simplify the controller to be designed.In this situation,the form of Lemma 1.4 is much simpler than that in Lemma 1.3.Furthermore,the estimated settling time is more accurate than those in existing literature.

Consider a nonlinearly coupled complex network consisting ofNnodes described by

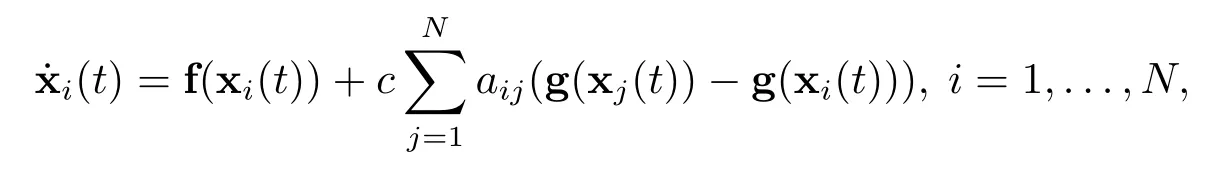
where xi(t)=(xi1(t),...,xin(t))>denotes the state vector of nodei,nonlinear function f(xi(t))=(f1(xi(t)),...,fn(xi(t)))>represents the dynamical behavior of thei-th node,c>0 is the coupling gain.g(xj(t))=(g1(xj1(t)),...,gn(xjn(t)))>∈Rnis the nonlinear coupling function.Besides,A=(aij)∈RN×Ndenotes the outer coupling matrix,in which,aij>0 if thei-th node can receive the information from nodej;otherwise,aij=0.In addition,aii=0.The Laplacian matrixL=(lij)∈RN×Nis defined asand the o ff-diagonal elementslij=−aij.Therefore,the controlled complex network can be written as

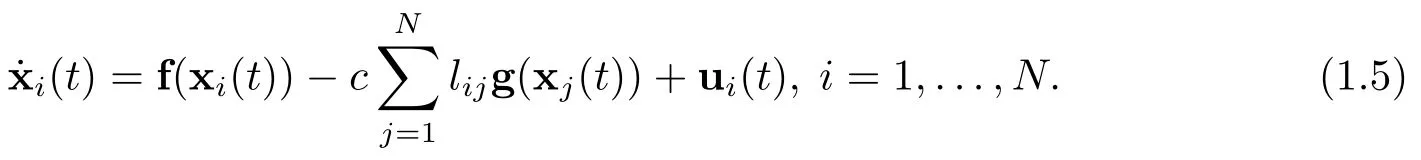
In this paper,complex network(1.5)is assumed to be symmetrical,the initial value is xi(0)=xi0,i=1,...,N,and complex network(1.5)is supposed to synchronize to the same state s(t)satisfying

in which s(t)=(s1(t),...,sn(t))>with initial value s(0)=s0.

Let ei(t)=xi(t)−s(t)be the error state,then one can get

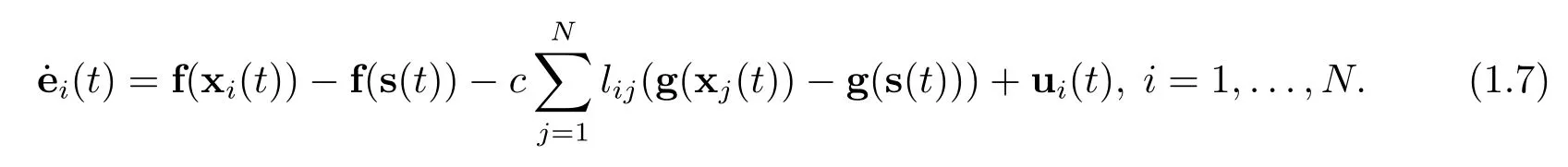
In order to proceed further analysis,the controller is designed as

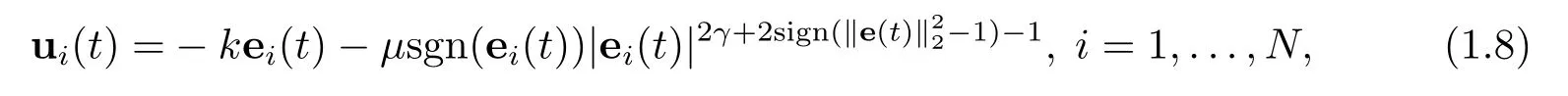
Remark 2In existing literature,the controller is usually designed as“ui(t)=−kei(t)−bsgn(ei(t))|ei(t)|α−csgn(ei(t))|ei(t)|β”,which consists of three terms:the first term is the linear feedback term,the index of the second term satisfies 0<α<1,and that of the last one satisfiesβ>1.Controller(1.8)proposed here only contains two terms,which is obviously more economical and practical.

(H1)The dynamical function f(·)of complex network(1.5)satisfies the usual Lipschitz condition.That is,for∀u,v∈Rn,there exists a positive constantρsuch that

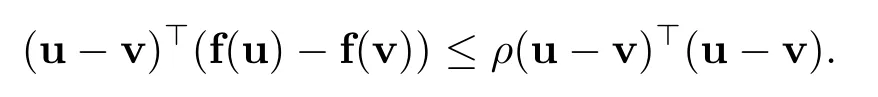
(H2) As for the nonlinear functiongk(·),k=1,...,n,we assume that there exist positive constants%k,such that for allx,y∈R,we have

Theorem 1.5Suppose that(H1)−(H2)holds.Then complex network(1.5)and target system(1.6)will reach fixed-time synchronization with controller(1.8),if there exist positive constantsksuch that

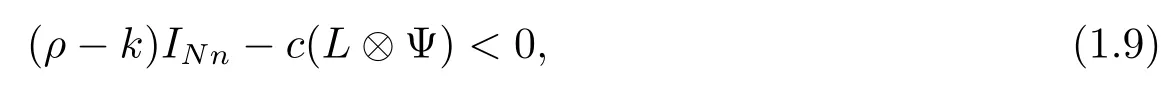
where Ψ =diag{%1,...,%n},ρand%k,k=1,...,npresented in(H1)and(H2),respectively.Furthermore,the settling time is estimated as

Remark 3From Theorem 1.5,condition(1.9)can be guaranteed ifk≥ρbased on the non-negative eigenvalues of matrixL.

2 Numerical Example

Example 1Theorem 1.5 is verified in this section.Consider a network consisting of 10 nodes,with the dynamics of each node being described by a three-dimensional complex network[4],where the inner coupling matrix Γ =I3,dynamical function f(xi(t))=−Cxi(t)+Mh(xi(t)),h(xi(t))=0.5(|xi1+1|−|xi1−1|,|xi2+1|−|xi2−1|,|xi3+1|−|xi3−1|)>,and

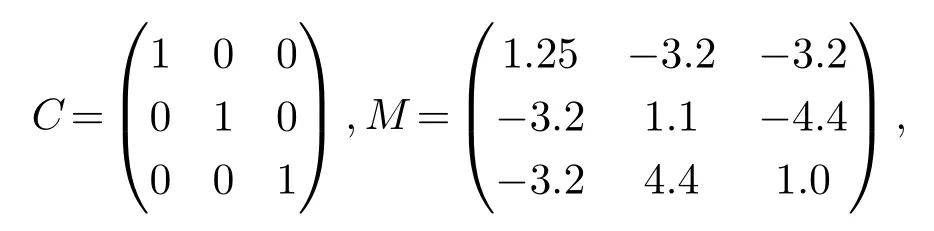
nonlinearly coupled function is defined as

Based on ei(t)=xi(t)−s(t),the controlled error system is

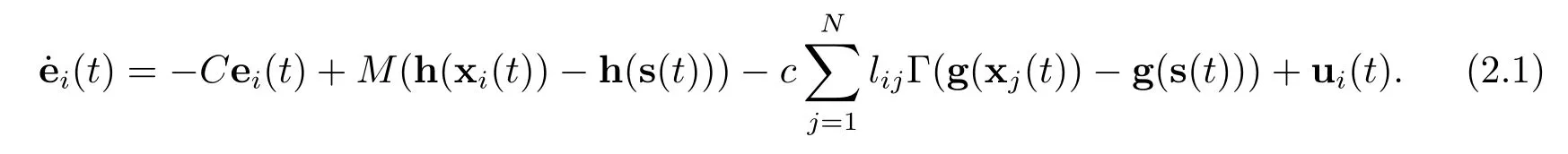
The evolution of 2-norm of the error states is shown in Panel(a)of Fig.1.Obviously,the error systems will not stabilize to the origin if no controllers are exerted.In the following,we consider the controlled network(1.5).

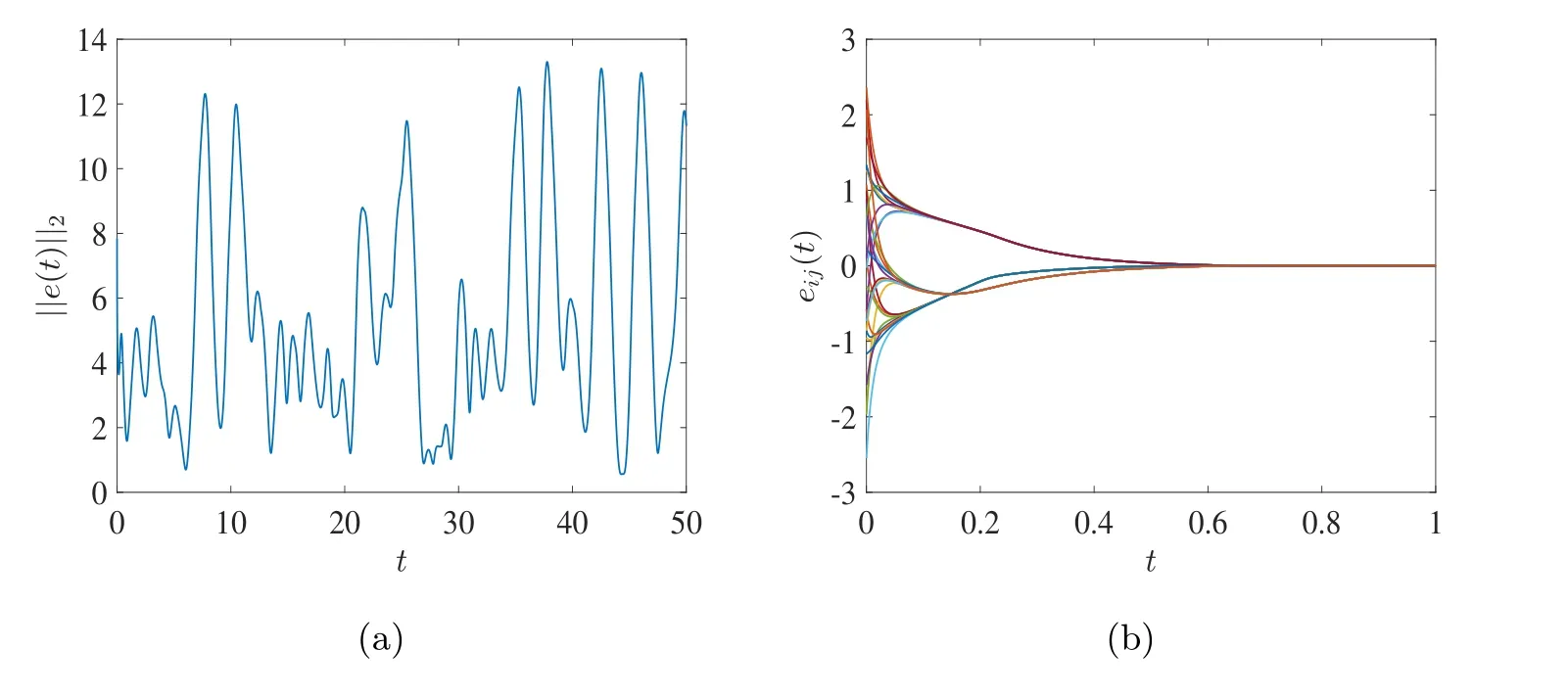
Figure 1 (a)Evolution of the 2-norm of the error states without controllers;(b)Evolution of error system(2.1).

According to the definitions of f(xi(t))and g(xi(t)),takingρ=7.7,Ψ =diag{1.8,2.5,1.7}to satisfy(H1)and(H2),respectively.Therefore,k=7.7 is chosen to make Eq.(1.9)hold.The evolutions of the state variables with controller(1.8)are shown in Panel(b)withγ=1.5 andµ=0.1.

Panel(b)in Fig.1 shows that stability of error network(2.1)can be realized withint=0.7.Actually,T≈548 according to the settling time estimated in Theorem 1,which is larger than the real synchronization time,but is smaller than the conventional estimations[2]–[3].