环上含参变量的Boltzmann测度的对数Sobolev不等式

程 新,毛 闰,张正良

(1.武汉大学数学与统计学院,武汉 430072)

(2.重庆市第八中学校,重庆 401120)

1 引言

Poincaré不等式,传输不等式和对数Sobolev不等式是研究测度集中性的有力工具[1,2].在这三类不等式中,对数Sobolev不等式强于Talagrand传输不等式,Talagrand传输不等式不等式又强于Poincaré不等式,具体例子可分别参看文献[3,4].在文献[5]中,Qian,Ma,Zhang证明了Boltzmann测度在维数n≥3固定时关于参数h>0满足一致的对数Sobolev不等式,但是并没有讨论n=2的情形.在Ma与Zhang的文献[6]中,作者针对n=2的情形给出了Boltzmann测度比较精确的谱系,而且有趣的是:当h→∞时,谱系以h的速率趋于无穷大,即庞加莱常数以1/h的速率趋于0.本文将给出在n=2时,对数Sobolev常数CLS(µh)关于h>0的一致非0上下界,这在一定程度上也能表明三个不等式之间的强弱关系.下面先介绍一下Boltzmann测度以及相关不等式.

Boltzmann测度设Sn−1是Rn(n≥2)上的单位球面,µ是Sn−1上的标准Lebesgue测度,i.e.µ=σn−1/sn−1,其中σn−1为单位球面Sn−1上的均匀测度,sn−1:=nπn/2/Γ(1+n/2)为单位球面面积(归一化因子).对任意的h>0和e1=(1,0,...,0)∈Sn−1,单位球面Sn−1上的概率测度µh有如下表达式:

其中,cn(h)为归一化因子.称该概率测度µh为外磁场下的Boltzmann测度.特别n=2时,S1即为环,我们简记为S,对应测度µ2,h简记为µh,此即为本文所考虑的含参变量h的环上的Boltzmann测度.

下面介绍几个相关不等式:设M是一个完备黎曼流形,其上的测地度量记为d,∇为M上的梯度.M1(M)为M上的概率测度空间.

Poincar不等式我们称测度µ∈M1(M)满足 Poincar不等式(记µ∈PI(C)),若对任意光滑函数f:M→R,都存在非负常数C使得

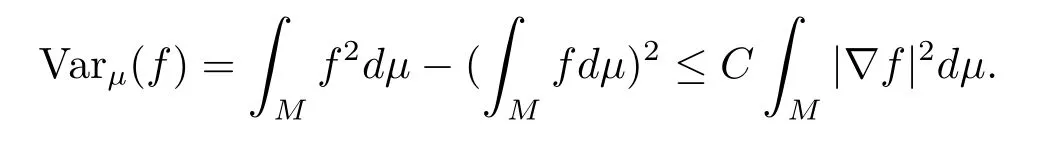
记CP(µ) 为最佳 Poincar常数.

Lp传输不等式称测度µ满足Lp传输不等式,若对任意的ν=f2µ∈M1(M),都存在非负常数C使得

其中Wp(ν,µ)是测度ν和µ的Lp-Wasserstein距离,其定义如下:

这里π是M×M上的概率测度,其边缘分布为µ,ν.记CWpH(µ)为满足该不等式的最佳常数.

对数Sobolev不等式称测度µ满足对数Sobolev不等式,若对任意光滑函数f:M→R,都存在非负常数C使得

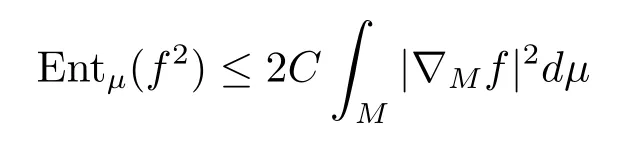
成立,其中Entµ(f2):=µ(f2logf2)−µ(f2)log(µ(f2))为函数f2关于µ的熵.记CLS(µ)为最佳对数Sobolev常数.

2 准备工作

本文沿用[7,8]中的降维方法:设νh为µh在映射x→d(e1,x)下的像测度,则νh为[0,π]上的概率测度,其概率密度为为归一化因子.

在处理环上测度的对数Sobolev不等式时可参考如下的降维定理.

定理2.1[8]设µ为环S上的均匀测度,M为S上的概率测度,其定义如下

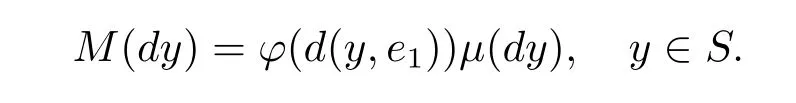
其中,ϕ是非负可测的.设M在映射y→d(y,e1)下的像测度为ν,则最佳对数Sobolev常数满足其中,λDD(ν) 是满足 [0,π]上 Dirichlet 边界条件的ν的第一特征值.

而对于本文中所考虑的Boltzmann测度对应的λDD(νh)也有如下估计.

引理2.2[6]对于任意h>0,对任意的光滑函数f:S→R,νh为Boltzmann测度µh在映射x→d(e1,x)下的像测度,则Dirichlet边界条件下的第一特征值λDD(νh)满足

在上面两个结论的基础上,本文的讨论将主要集中在[0,π]上的一维测度νh上.针对一维测度,Barthe和Roberto在[9]中给出了关于对数Sobolev不等式的刻画,现陈述如下.

定理2.3[9]设µB,νB是R 上的Borel测度,其中µB(R)=1且dνB(x)=n(x)dx,n(x)为一绝对光滑函数.设m是测度µB上的中位数,且对任意光滑函数f:R→R,满足

其中,CLS为最佳对数Sobolev常数.则有max(b−,b+)≤2CLS≤4max(B−,B+),其中

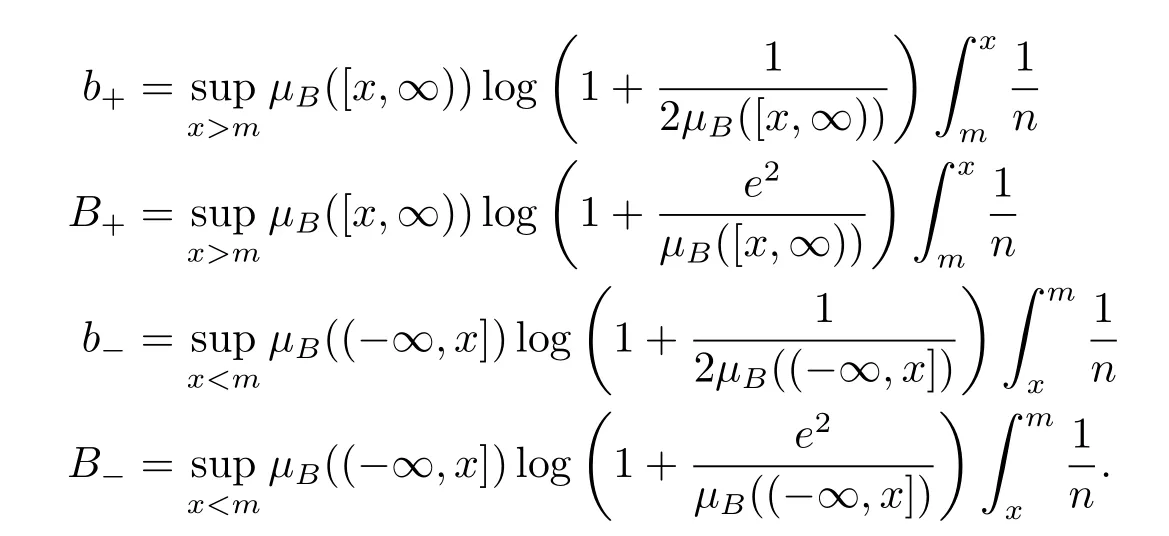
注意到,对于任意0≤y≤1/2,都有因此,B+≤4b+且B−≤4b−.不难发现,此时最佳对数Sobolev常数CLS满足max(b−,b+)≤2CLS≤16max(b−,b+).本文的目的仅在于给出常数阶,故此证明也只需去估计b−,b+.为此还需下面几个估计.

引理2.4设则

3 主要结论

定理3.1对于任意h>0,νh为Boltzmann测度µh在映射x→d(e1,x)下的像测度,则νh满足一致的对数Sobolev不等式,即对于任意光滑函数f:S→R,有其中对数Sobolev最佳常数CLS(νh)一致有界,且满足

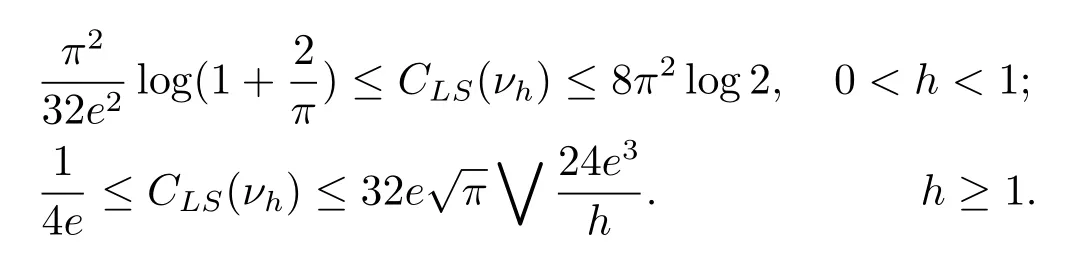
进而有,环S上的Boltzmann测度µh满足一致的对数Sobolev不等式,且最佳常数CLS(µh)满足

注从定理结论中我们可以看出,对于任意的h>0,CLS(µh)=O(1).而在[6]中,作者给出了该测度谱系的比较精确的刻画此即说明 Poincaré常数CP(µh)=1/λ1(µh)=O(1/h),再通过[10]中的结论,我们还可知道Talagrand传输不等式常数此也可佐证对数Sobolev不等式严格强于Talagrand传输不等式.

4 定理3.1的证明

根据降维定理2.1,我们仅需考虑一维测度νh,再由定理2.3,考虑如下的b+,b−

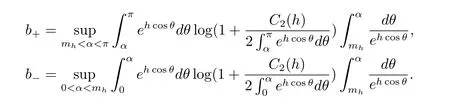
讨论将分两种情形展开.

情形10

其次,考虑b+的上界.因对任意在x>0上都是单调递增的,故有