一组等价蔡氏忆阻混沌电路的设计

徐 影，陈菊芳

(东北师范大学 物理学院，长春 130024)

忆阻器[1]使电路设计的基础元件由电阻、 电容和电感增加到4个. 忆阻器是一种有记忆功能的非线性电阻，其潜在的应用价值已引起人们广泛关注，其中利用忆阻器的非线性特征实现混沌电路是研究热点之一[2-5]. 忆阻器的磁通量φ与其累积电荷q间的关系可以用φ-q或q-φ平面上的一条曲线f(φ,q)=0确定[6-8]. 当f(φ,q)=0由磁通的单值函数表示时，称为磁控忆阻器，特性曲线的斜率W(φ)=dq(φ)/dφ称为忆导. 其电流与电压间的关系为i=W(φ)v. 蔡氏电路是典型的混沌电路，由于忆阻器具有非线性特性，因此用忆阻器替换蔡氏混沌电路中的蔡氏二极管，即可构成蔡氏忆阻混沌电路[9-10]，这些电路中均含有电感，但电感不易购买和制作，且不易集成. 忆阻器有多种模型，其中三次光滑型忆阻器是最常用的，其磁通量φ与电荷q间的关系为q(φ)=aφ+bφ3，由此可得忆导为W(φ)=a+3bφ2，其中a,b>0. 本文以该模型为例，通过改变元件参数，将不同结构的RC正弦波荡电路与等效的LC并联回路耦合，等效为LC并联谐振回路，设计了4种等价的蔡氏忆阻混沌电路，并对其进行电路仿真，得到与理论分析和数值计算一致的实验结果.

1 等价蔡氏忆阻混沌电路的设计

经典的蔡氏忆阻混沌电路如图1所示，其中虚线左侧为LC并联谐振回路，右侧的-G为负阻，W为磁控忆阻器. 端口a，b左侧的输入导纳为

Y=jωC+1/(r+jωL).

(1)

由电路理论可知，任何线性单端口电路，若端口输入导纳的表达式与Y相同，则与图1电路的LC回路等效，将其与虚线右侧的电路连接即可构成等价的蔡氏忆阻混沌电路.

1.1 等价蔡氏电路1

等价蔡氏忆组混沌电路1如图2所示，其中虚线左侧电路为经典的文氏桥电路，通常作为正弦波振荡电路，放大倍数为A=1+Ra/Rb, 当满足A≥1+R3/R2+C2/C3时，可产生正弦波振荡. 改变元件参数也可等效为LC并联回路. 由电路可求得端口a，b左侧的输入导纳Y1为

(2)

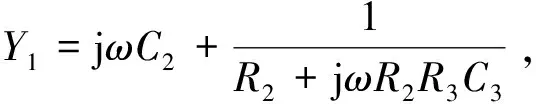
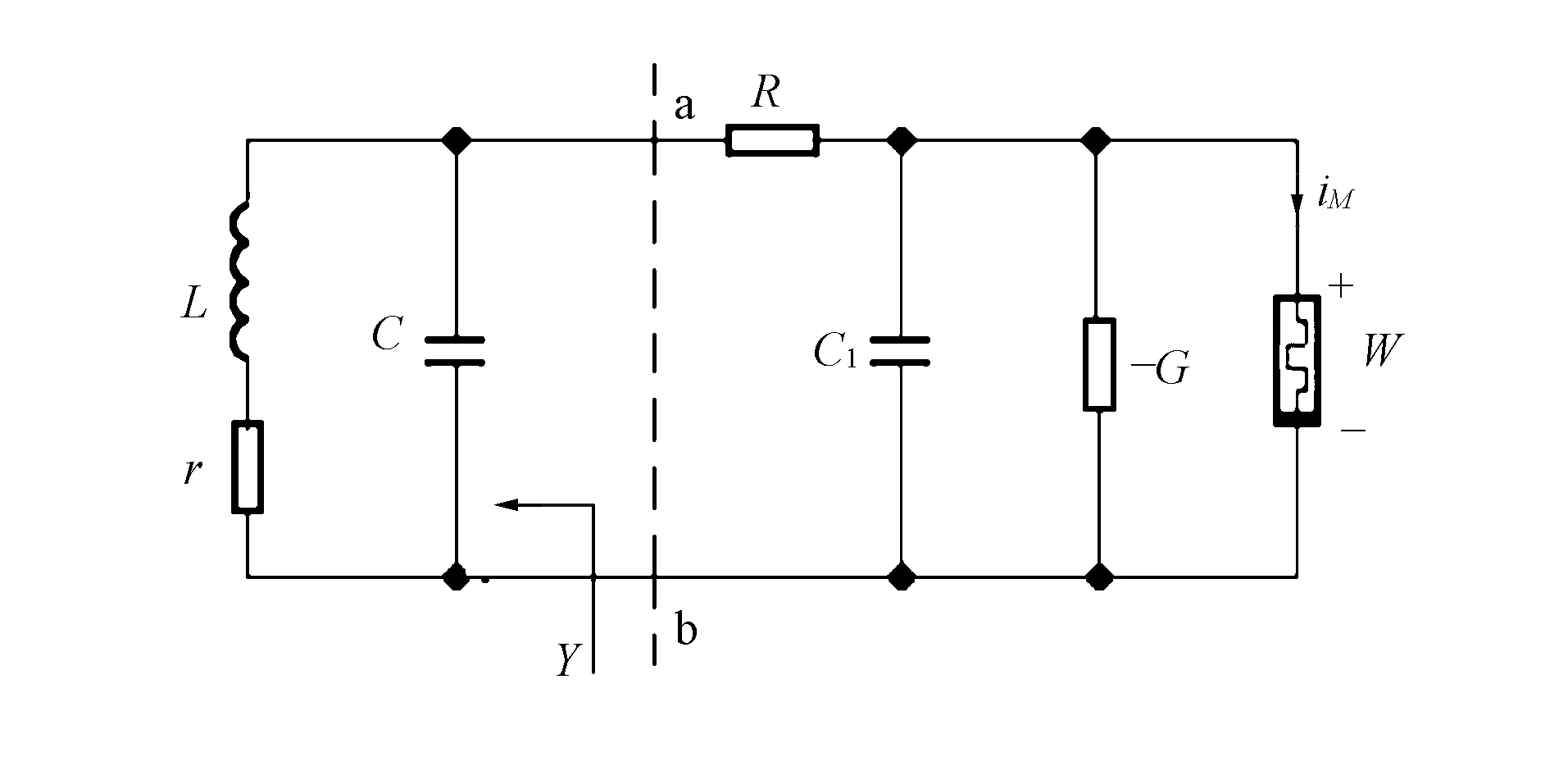
图1 经典的蔡氏忆阻混沌电路Fig.1 Classical Chua’s memristive chaotic circuit

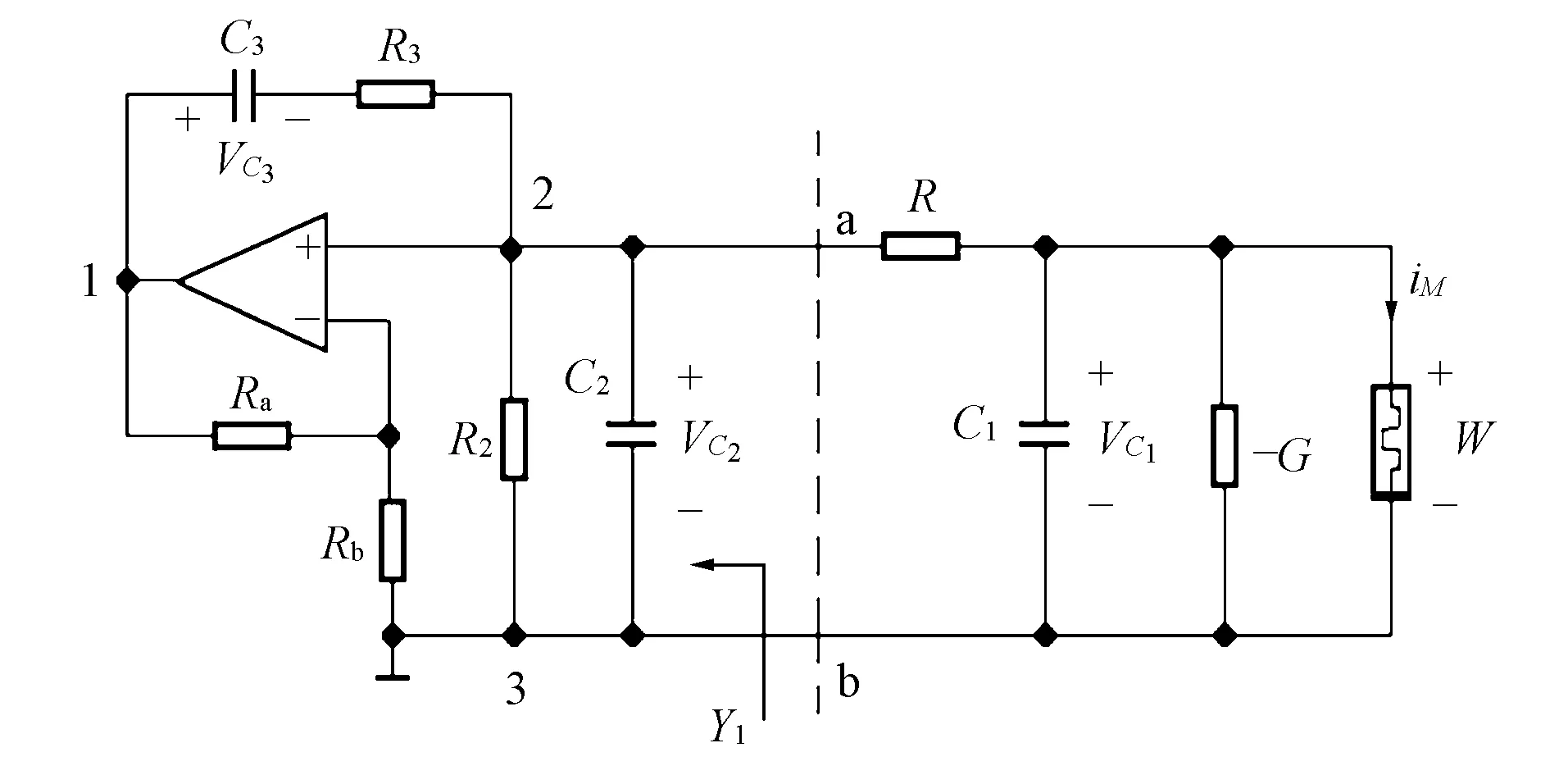
图2 等价蔡氏忆阻混沌电路1Fig.2 Equivalent Chua’s memristive chaotic circuit 1

根据Kirchhoff电压定律(KVL)和电流定律(KCL)，可得图2电路的状态方程为

(3)

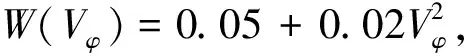
选取C1=1.25 nF，即对应α=16，电路的吸引子如图5所示. 由图5可见，吸引子为双涡卷状，忆阻器的伏安特性呈斜“8”型结构.

图3 y随α变化的分岔图Fig.3 Bifurcation diagram of y with α

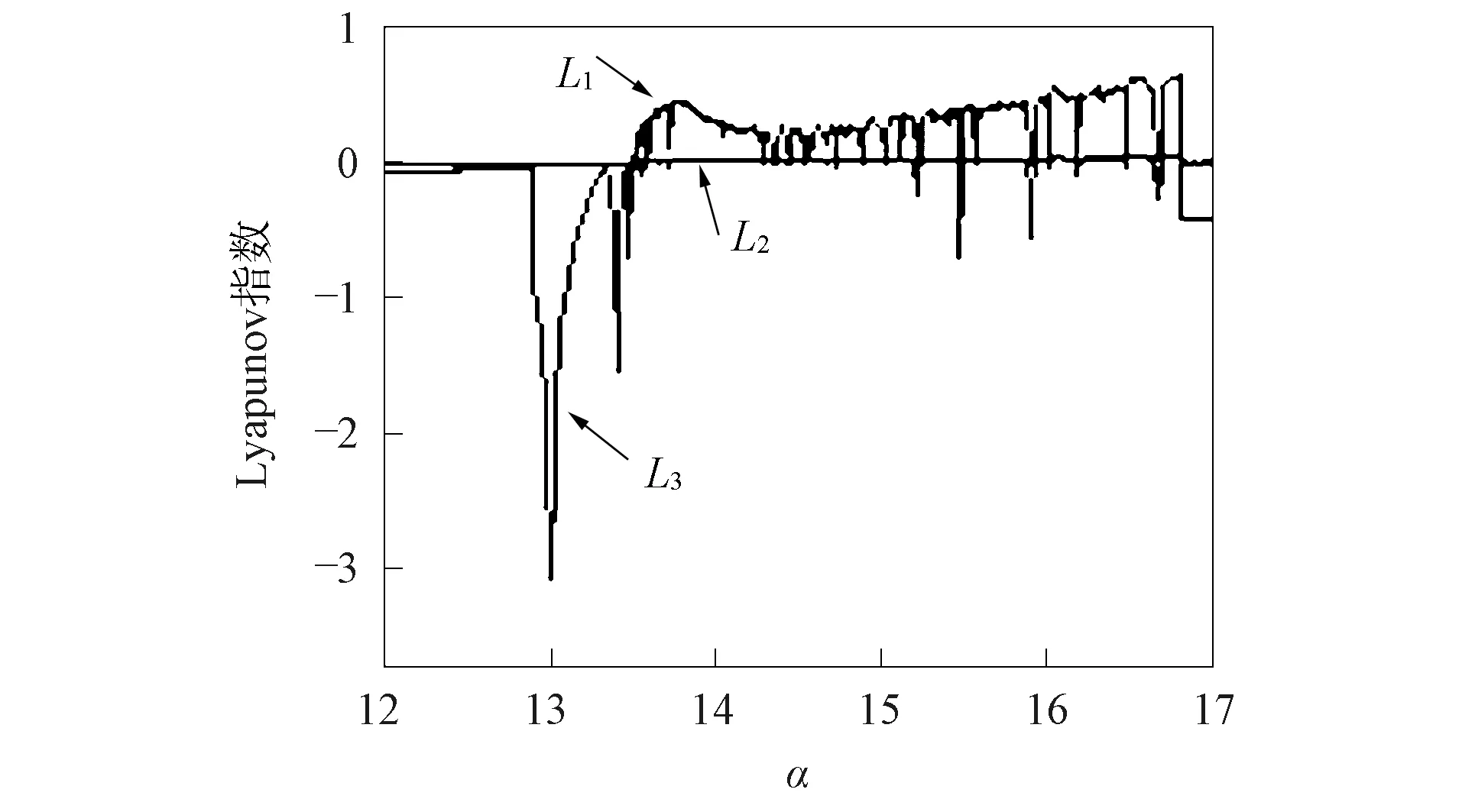
图4 Lyapunov指数谱Fig.4 Lyapunov exponential spectra

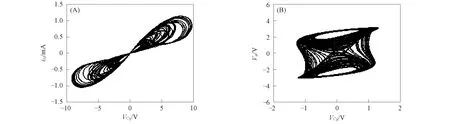
图5 混沌吸引子Fig.5 Chaotic attractors

1.2 等价蔡氏电路2

将图2电路中的串联支路R3C3与电阻Rb互换，其他元件不变，即可形成等价蔡氏忆组混沌电路2, 如图6所示，虚线左侧电路仍可产生正弦振荡，产生正弦波振荡的条件与图2相同. 改变元件参数也可等效为LC并联回路. 端口a，b的输入导纳Y2为

(4)

显然，Y2=Y1，等价条件与图2相同. 与图2相比，由于图6中的电容C3可单端接地，因此易于测量和提取电压VC3. 根据等效电路的理论可知，当图2与图6电路对应元件取值相同时，电压VC1，VC2和Vφ分别对应相同，但电容C3的电压不同，可通过电路的状态方程求得.

由图6可得电路的状态方程为

(5)

若令μ=R/R2，β=RC2/(R3C3)，γ=RC2/(R3C3), 在与图2电路对应元件取值相同的条件下，则可得μ=30，β=0.5，γ=0.5，其他系数均相同. 将方程(5)进行标量变换，令VC32=0.2VC3，得到的方程与式(3)相同.

1.3 等价蔡氏电路3

等价蔡氏忆阻混沌电路3如图7所示, 虚线左侧的选频电路为单周期T选频电路，电压放大倍数A=1+Ra/Rb，若A≥1+C2/C3+R3C2/(R2C3)，则电路为正弦波振荡电路. 改变元件参数也可等效为LC并联回路. 端口a,b的输入导纳Y3为

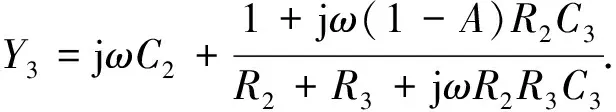
(6)

先令A=1, 再将式(6)与式(1)对应可知，令C=C2，L=R2R3C3，r=R2+R3，虚线左侧电路可等效为LC并联回路. 若仍设C=20 nF，L=48 mH，r=0.2 kΩ, 可选取R2=0.1 kΩ，R3=0.1 kΩ，C2=20 nF，C3=4.8 μF，Ra支路短路，Rb支路断路.

图6 等价蔡氏忆阻混沌电路2Fig.6 Equivalent Chua’s memristive chaotic circuit 2

图7 等价蔡氏忆阻混沌电路3Fig.7 Equivalent Chua’s memristive chaotic circuit 3

由图7可得电路的状态方程为

(7)

若令μ=R/R3，β=RC2/(R2C3)，γ=RC2/(R2C3)+RC2/(R3C3)，仍选择R=6 kΩ，则可得μ=60，β=0.25，γ=0.5. 当图7与图2电路对应元件取值相同时，令VC33=0.1VC3，标量变换后得到的方程与式(3)相同. 表明图7与图2电路中的电压VC1，VC2和Vφ分别相同，电压VC33是图2电路VC3的0.1倍.

1.4 等价蔡氏电路4

等价蔡氏忆阻混沌电路4如图8所示, 虚线左侧的选频电路仍为单周期T选频电路，与图7电路的单T选频电路为对偶电路. 若电压放大倍数A≥1+R3/R2+R3C2/(R2C3)，电路仍可产生正弦振荡. 改变元件参数也可等效为LC并联回路.

图8 等价蔡氏忆阻混沌电路4Fig.8 Equivalent Chua’s memristive chaotic circuit 4

端口a,b的输入导纳Y4为

(8)

令R2Ra=R3Rb，将式(8)与式(1)对应可知，虚线左侧的电路可等效为LC并联回路，其中C=C2，L=R2R3C3，r=R3. 若仍设C=20 nF，L=48 mH，r=0.2 kΩ，可选取R2=1 kΩ，R3=0.2 kΩ，C2=20 nF，C3=240 nF，Ra=0.2 kΩ，Rb=1 kΩ.

由图8可得电路的状态方程为

(9)

若令μ=R/R3，β=RC2/(R2C3)，γ=RC2/(R2C3)，仍选择R=6 kΩ，则可得μ=30，β=0.5，γ=0.5. 当图8与图6电路对应元件取值相同时，方程(9)与方程(5)相同，图8与图6电路对应的电压也相同.

2 电路仿真的实验结果

利用Multisim电路仿真软件对上述4个等价蔡氏忆阻电路进行仿真实验. 其中负阻电路如图9所示，采用运放AD844，将其连接成电流传送器的形式，根据电流传送器的电气特性，可得输入电导G=-1/RN. 该电路结构简单，易于调节. 实验选取RN=4 kΩ，对应G=-0.25 mS.

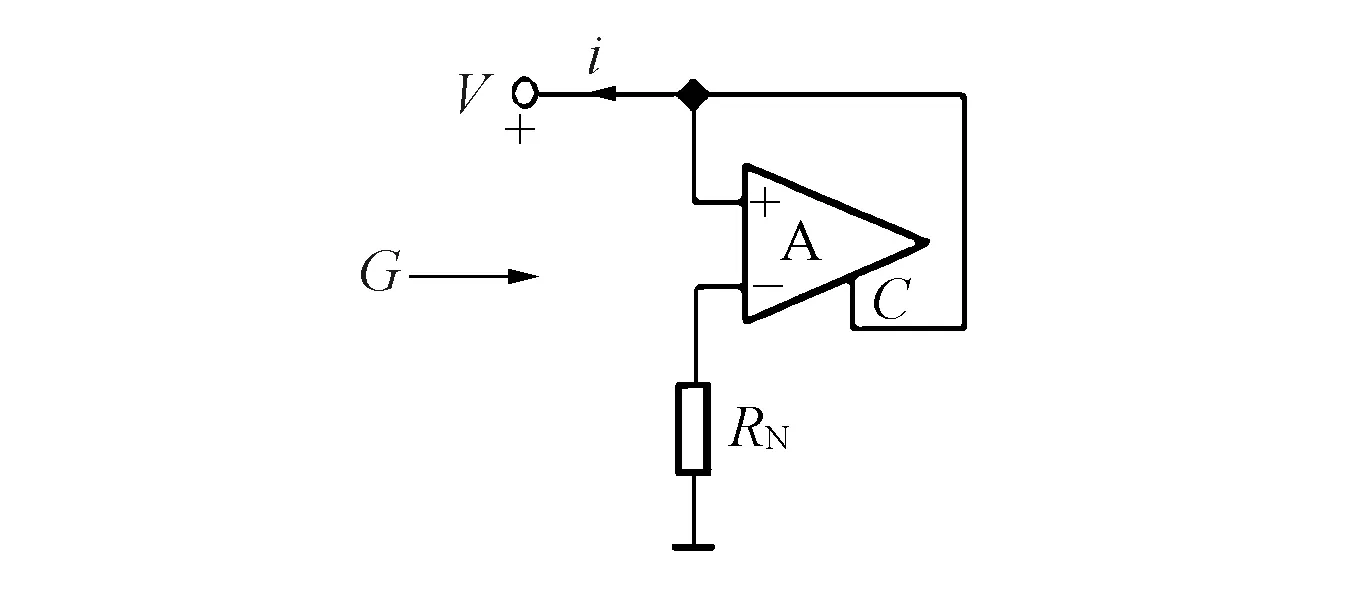
图9 负阻电路Fig.9 Negative resistance circuit

忆阻器的模拟等效电路如图10所示. 运放A3构成反向积分器，其输出电压

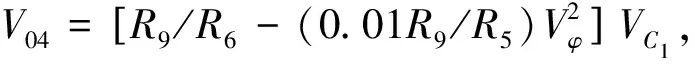
得到相应忆导值的表达式为

(10)

对应a=1/R10-R9/(R6R10), 3b=0.01R9/(R5R10) .

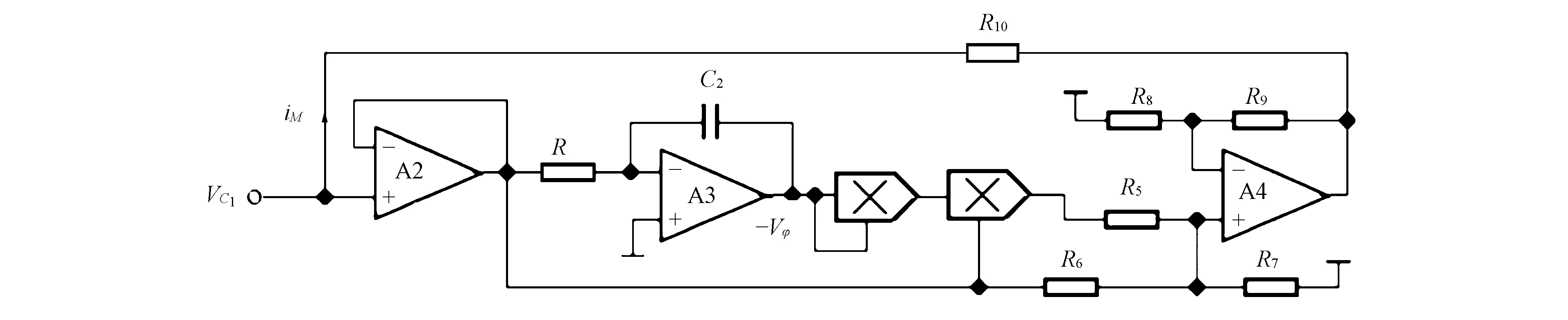
图10 忆阻器电路Fig.10 Memristor circuitt

为方便观测忆阻特性，选取R10=1 kΩ，若电阻R10两端获得1 V电压，则对应于1 mA的忆阻器电流iM. 通过示波器获得的R10两端电压均转化为电流iM表示. 选取R7=R9=10 kΩ，R5=5 kΩ，R6=10.53 kΩ，R8=3.4 kΩ，对应a=0.05 mS，3b=0.02 mS/V2.

电路仿真结果如图11所示, 其中： (A)为忆阻器的伏安特性曲线； (B)，(C)，(D)分别为图2、 图6、 图7电路中电容C3的电压与Vφ吸引子. 由图11(A)可见，4个等价蔡氏电路的忆阻特性曲线均相同； 由图11(B)～(D)可见，其Vφ均相同，但电容C3的电压不同，实验结果与数值计算结果基本一致，存在较小的误差是由于忆阻器中的积分误差所致.

图11 电路仿真结果Fig.11 Results of circuit simulation

综上，本文以磁控忆阻器为例，利用运放和不同的RC选频电路代替LC并联谐振回路，设计了4种等价的蔡氏忆阻混沌电路. 电路结构简单，调节方便，电路性能更稳定，并进行了电路仿真，所得实验结果与理论分析结果一致. 本文的设计方法适用于蔡氏忆阻混沌电路及非忆阻蔡氏混沌电路.