含x|x|的变形蔡氏电路系统的同步研究

张文琦

(山西农业大学 文理学院，山西 太谷 030801)

随着计算机科学技术的飞速发展，极大促进了非线性科学的蓬勃发展，使得人们发现了混沌并加强了对混沌的了解[1].混沌现象是非线性系统的一种重要运动形式已成为人们的共识.如何利用具有蝴蝶效应的混沌运动为人类服务是目前不断探索和深入研究的问题[2].在混沌同步领域提出了大量的控制方法如：线性反馈同步法[3]、FSHPS (full-state hybrid projective synchronization)[4]、延时反馈同步法[5]等.由蔡少棠教授设计的三阶非线性自治电路是一种产生混沌振荡的典型非线性电路，在此基础上产生的变形蔡氏电路系统具有更为复杂的非线性动力学行为[6].本文针对含x|x|的变型蔡氏电路系统的同步问题进行了研究，运用主动控制方法令两系统自同步，在此基础上运用自适应主动控制方法实现了参数不确定的两系统同步.

1 变形蔡氏电路

用函数x|x|替代蔡氏电路中分段函数可得变形蔡氏电路.方程如式(1):

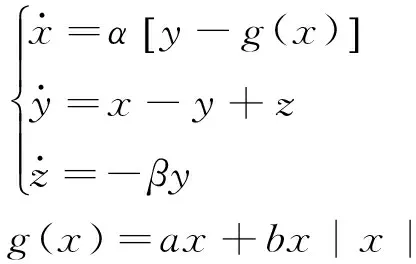
(1)

式中x,y,z为无维变量，α,β是大于零的参数，β=14.0,a=-1/6,b=1/16.当α较小时，系统有稳定的平衡点，随着α的值的增大,系统产生Hopf分岔，此时可以观测到小段的周期轨线.而当α的值进一步增大时，系统逐步形成了2个不对称的混沌吸引子，而且这2个混沌吸引子越靠越近，最终形成双涡旋混沌吸引子[7].

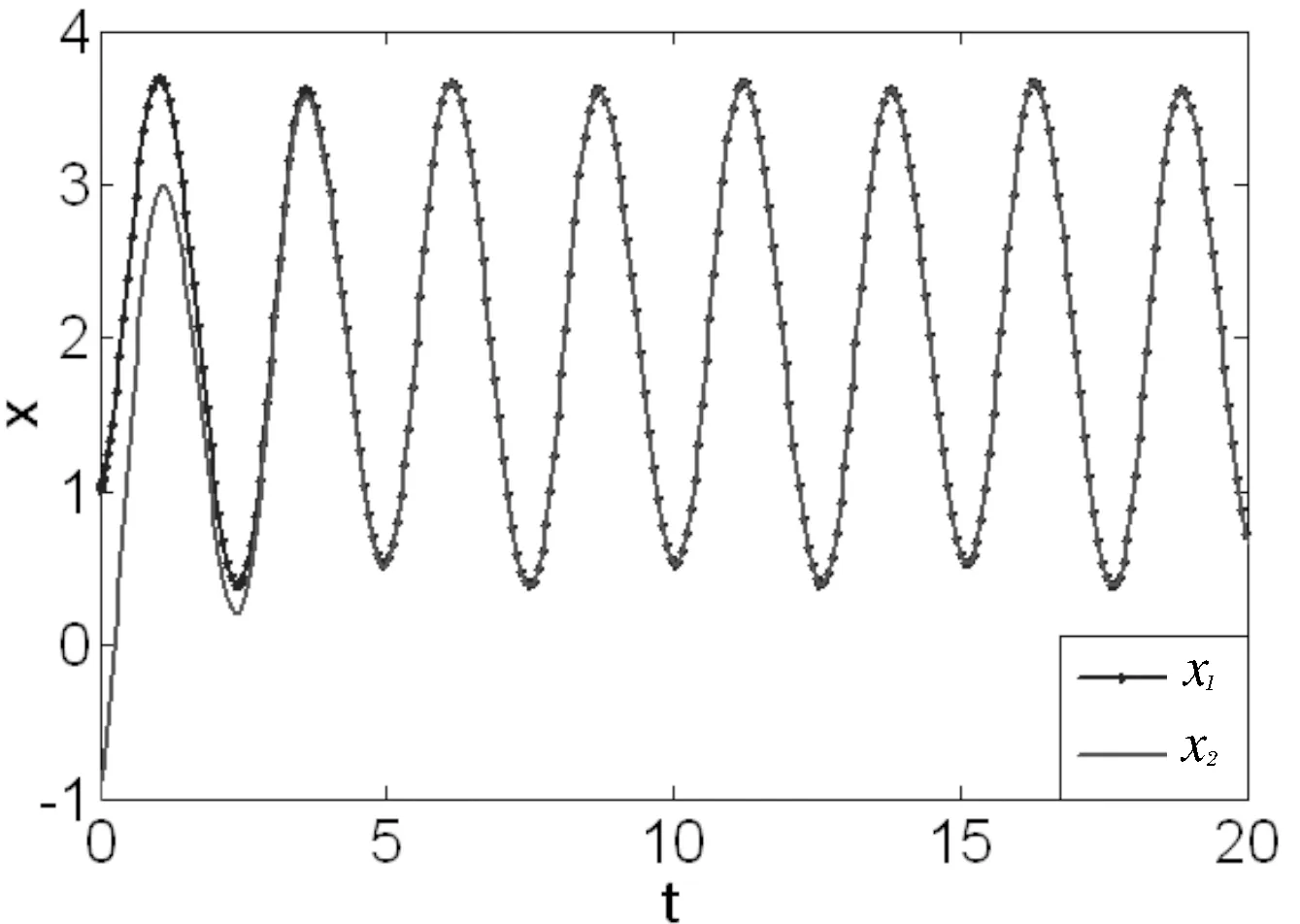
图1 变型蔡氏电路同步仿真图

2 主动控制达到变形蔡氏电路系统同步

显然,参数α对变形的蔡氏电路系统性质起着主要作用.因此由式(1)在不相同的初值，不相同的已知的参数α条件下构建的式(2)与式(3)分别代表驱动系统与响应系统.系统方程表示如下：

(2)

(3)

本文的目的是找到一控制器u=[u1,u2,u3]T使得响应系统与驱动系统同步.式(2)与式(3)相减得到如下的误差动力系统为：

(4)

这里e1=x2-x1,e2=y2-y1,e3=z2-z1.

变形蔡氏电路系统混沌同步是指取得对误差系统零解的渐近稳定.变形蔡氏电路系统中g(x)的实际状态已被描述.因此，如果系统参数能被确切估量，则主动控制函数能用下式描述：

u1=α′(g(x2)-y2)-α(g(x1)-y1)-e1，u2=-e1-e3，u3=βe2-e3

(5)

选取合适控制信号，使误差系统(4)有特征值(-1，-1，-1)，则随着时间趋于无穷时，将使误差系统e(t)=[e1,e2,e3]T收敛于0.因而使两个变形的蔡氏电路系统达到混沌同步.令α=8.835,α′=9.027,β=14.0,驱动系统的初始条件为{x(0)=1.01,y(0)=z(0)=0.01}，响应系统的初始条件为{x(0)=-1.01,y(0)=z(0)=-0.01}.图1为两个变形蔡氏电路系统的主动控制的仿真结果.发现在t=5时，驱动系统与响应系统达到同步.

3 自适应主动控制达到变形蔡氏电路系统同步

由上述可知，在控制过程中，驱动与响应系统的系统参数对控制器起着重要作用.然而，在实际系统中，参数往往是事先不能精确知道的.假定驱动与响应变形蔡氏电路系统有不同的初始条件但有相同却未知的参数.本文的目标是设计一控制器u=[u1,u2,u3]T使得所有的参数独立，然后对参数更新使得驱动与响应系统渐近同步.

由式(4)构造一Lyapunov函数：

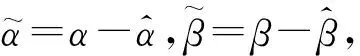
采用自适应主动控制法，即设计一控制器u以及对估计参数确定一如下的更新法则：

(6)

e1(αe2-αg(x2)+αg(x1)+u1)+e2(e1-e2+e3+u2)+

图2 变型蔡氏电路同步仿真图

因此，两个变形蔡氏电路系统的混沌同步是能实现的.而且，很明显，式(6)中的控制器是未知独立参数.

4 结论

本文有效的实现了变形蔡氏电路系统的自同步，而且对于参数不确定的变形蔡氏电路系统，采用自适应主动控制法实现其混沌同步.对于实际应用中含有不确定参数的非线性系统的混沌同步提出了一种可行的同步方式.

[1]刘秉正,彭建华.非线性动力学[M].北京:高等教育出版社,2004:469-470.

[2]王兴元.复杂非线性系统中的混沌[M].北京:电子工业出版社,2003:1-14.

[3]Liu F,Ren Y,Shan X M,et al.A linear feedback synchronization theorem for a class of chaotic system [J].Chaos Solitons & Fractals,2002,13(4):723-730.

[4]Wen GL,Xu D.Nonlinear observer control for full-state projective synchronization in chaotic continuous-time systems [J].Chaos Solitons & Fractals,2005,26:71-77.

[5]陈艳艳,彭建华,刘秉正,等.增强型延迟反馈法控制低维混沌系统的解析研究[J].物理学报,2002,51(7):1 489-1 496.

[6]Chua L O,Itoh M,Kocarev L,et al.Chaos synchronization in Chua′s circuits[J].Journal of Circuit, Systems and Computers,1993,3(1):93-108.

[7]邓杰生,文剑锋,钟国群,等.Modified Chua′s circuit withx|x|[J].控制理论与应用,2003,20(2):223-227.

[8]张文琦,杨丽新.蔡氏电路的两种变型[J].重庆工学院学报:自然科学版,2007,21(1):120-123.