关于 Diophantine方程 xd(n)+yφ(n)=zσ(n)

管训贵

(泰州师范高等专科学校数理系,江苏泰州 225300）

关于 Diophantine方程xd(n)+yφ(n)=zσ(n)

管训贵

(泰州师范高等专科学校数理系,江苏泰州 225300）

对于正整数n=2tpa11pa22…pakk,这里pi是奇素数,mi是正整数,i=1,2,…,k,2＜p1＜p2＜…＜pk,t是非负整数.设d(n),φ(n),σ(n)分别表示n的约数函数,Euler函数和约数和函数.给出了:n=2和 3时,方程xd(n)+yφ(n)=zσ(n)正整数解的一般公式;并证明了ai(i=1,2,…,k)中至少有两个为奇数或存在i及奇素数p,使pi≡1(modp)且ai≡ -1(modp)两种情形时,方程xd(n)+yφ(n)=zσ(n)没有正整数解.

高次 Diophantine方程;约数函数;Euler函数;约数和函数;正整数解;素数

1 引言及主要结论

对于正整数n,设d(n),φ(n),σ(n)分别表示n的约数函数,Euler函数和约数和函数.J.Sandor[1]提出了方程:

的求解问题.2009年,乐茂华[2]证明了:当n无平方因子时,除了n=2或者n是适合n≡3(mod 4)的奇素数这两种情形外,方程(1)没有正整数解.作为文献[2]的补充,本文证明了如下:

定理 1n=2时,方程(1)的全部正整数解为(x,y,z)=(a,b3-a2,b),这里a,b为正整数,a2＜b3;n=3时,方程(1)满足条件(x,y)=1的全部正整数解为(x,y,z)=(|6a2b2-a4-b4|,4ab(a2-b2),a2+b2)或(4ab(a2-b2),|6a2b2-a4-b4|,a2+b2),这里a＞b＞0,(a,b)=1,a,b一奇一偶.

定理 2 设正整数n=2tpa11pa22…pakk,这里k＞1,pi是奇素数,mi是正整数,i=1,2,…,k,2＜p1＜p2＜…＜pk,t是非负整数.若ai(i=1,2,…,k)中至少有两个为奇数或存在i及奇素数p,使pi≡1(modp)且ai≡-1(modp)时,方程(1)没有正整数解.

2 关键性引理

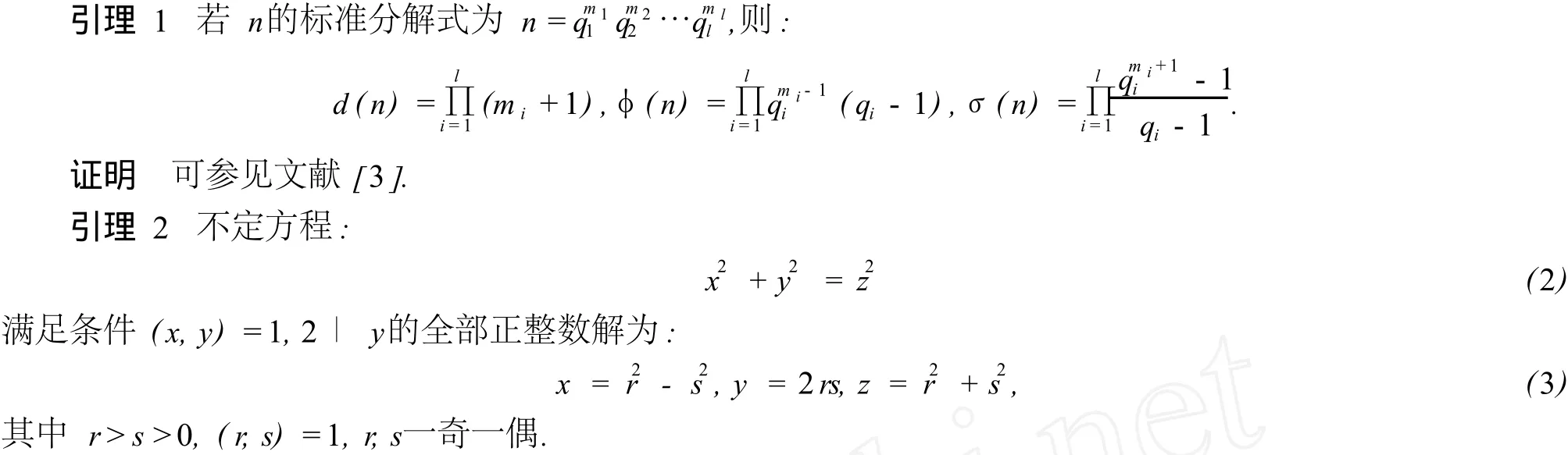
证明 可参见文献[4].

引理 3 不定方程:

假定式(4)有正整数解(x,y,z)满足(x,z)=1且z是所有解中最小的.显然 2łz且x是奇数或偶数.

如果x是奇数,则由式(4)结合引理 2得出:x2=a2-b2,y=2ab,z2=a2+b2,(a,b)=1,a＞b＞0.从而x2z2=a4-b4,即:b4+(xz)2=a4,(a,b)=1.这是式(4)的一个情形,但 0＜a＜z,与z最小矛盾.

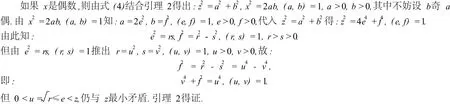
引理 4 (Fer mat大定理)若p为奇素数,则不定方程:xp+yp=zp,没有正整数解.

证明 可参见文献[5].

3 定理的证明

3.1 定理 1的证明

1)n=2时,由引理 1可知:d(n)=2,φ(n)=1,σ(n)=3.于是方程(1)变为:

令x=a,z=b,代入式(5)得:y=b3-a2,故方程(1)的全部正整数解为:

这里a,b为正整数,a2＜b3.

2)n=3时,由引理 1可知:d(n)=2,φ(n)=2,σ(n)=4.于是方程(1)变为:

设x,y,z是式(6)的正整数解,满足(x,y)=1,则x,y,z2是式(2)满足(x,y)=1的正整数解.因为x,y一奇一偶,不妨设 2∣y,由引理 2知:

其中r,s满足方程(3).因而r,s,z也是式(2)满足(r,s)=1的正整数解.

若 2|s,则由引理 2知:

此外,容易直接验证,式(10)、(14)满足方程(6).因此n=3时,方程(1)满足条件(x,y)=1的全部正整数解为:(x,y,z)=(|6a2b2-a4-b4|,4ab(a2-b2),a2+b2)或(4ab(a2-b2),|6a2b2-a4-b4|,a2+b2),这里a＞b＞0,(a,b)=1,a,b一奇一偶.定理 1得证.

3.2 定理 2的证明

由引理 3知,式(6)没有正整数解,从而方程(1)没有正整数解.

2)若存在i及奇素数p,使pi≡1(modp)且ai≡-1(modp),则有:

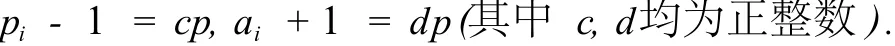
这时p∣d(n),p∣φ(n).

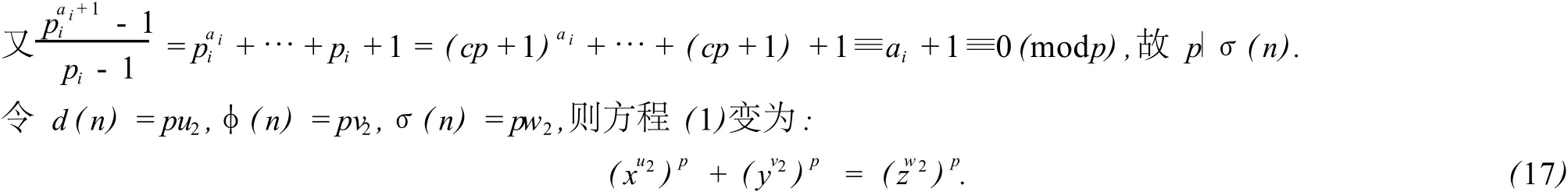
由引理 4知,式(17)没有正整数解,从而方程(1)没有正整数解.定理 2得证.

[1] Sandor J.Open question 2127[J].OctogonMathMag,2006,14(1):409.

[2] 乐茂华.关于 Diophantine方程xd(n)+yφ(n)=zσ(n)[J].湖北民族学院学报:自然科学版,2009,27(3):289-292.

[3] 华罗庚.数论导引[M].北京:科学出版社,1979.

[4] 闵嗣鹤,严士健.初等数论[M].北京:高等教育出版社,2004.

[5] Faltings G.The Proof of Fer mat’sLast Theorem by R.Taylor and A wiles[J].Notice AmerMath Soc,1995,42(7):743-746.

On the D iophantine Equationxd(n)+yφ(n)=zσ(n)

GUAN Xun-gui
(Depar tment ofMathematics&Physics,Taizhou Normal College,Taizhou 225300,China)

For any positive integern=2tpa11pa22…pakk,where pibe odd pr ime andmibe positive integer withi=1,2,…,k,2＜p1＜p2＜…＜pk,tbe a non-negative integer.Letd(n),φ(n)andσ(n)denote the divisor function,Euler′s totient function and the sum of distinct divisors ofnrespectively.In this paper,we obtained the general for mulas of positive integral solutions of equationxd(n)+yφ(n)=zσ(n)forn=2 and 3.We proved if(1)there are two odd numbers inai(i=1,2,…,k),or(2)there arei(i=1,2,…,k)and odd primep,such thatpi≡1(modp)andai≡ -1(modp),xd(n)+yφ(n)=zσ(n)has no positive integral solutions(x,y,z).

higherDiophantine equation;divisor function;Euler′s tontine function;sum of distinct divisors;positive integral solution;prime

O156

A

1008-8423(2010)02-0147-03

2010-05-28.

泰州师范高等专科学校重点课题资助项目(2009-ASL-04).

管训贵 (1963-),男,副教授,主要从事基础数论的研究.