几何尺寸对空气喷射器性能的影响研究

周三平，张 瓒

（西安石油大学机械工程学院，陕西 西安 710065）

喷射器是一种利用高压流体来抽吸低压流体的流体机械，具有结构简单、维修便捷、易于实现自动化、对环境污染小等优点，被广泛用于电力、制冷、石油、化工等领域，喷射器的结构与性能越来越被人们重视。

喷射器的喷嘴及各部分的结构对喷射器性能有重要影响，目前的研究多是针对喷嘴的结构形状对喷射器性能的影响。薛康康等[1]对喷嘴形状进行了优化，提出采用花瓣形喷嘴，用提高气流混合效率的方法来提升喷射器性能。王雨风等[2]通过优化喷嘴段结构参数来提高喷射效率。刘昌鹏等[3]采用更适合两相流动的等速度梯度数学方法，来优化喷射器喷嘴的型线，以得到良好品质的出口流场。还有许多专家学者对喷嘴之外的其余结构及工作参数进行了研究[4-8]，但对喷射器的喷嘴距、混合室出口截面积与喷嘴临界截面积之比、混合室的长度与直径之比等结构参数对喷射器性能影响的研究不多。

本文运用计算流体力学数值模拟软件Fluent，对空气喷射器的喷嘴距、混合室出口截面积与喷嘴临界截面积之比、混合室的长度与直径之比等结构参数进行了二维数值模拟，以获得喷射器的几何尺寸对喷射系数及喷射器喷射效率的影响规律。

1 几何模型与网格划分

1.1 几何尺寸

喷射器主要由喷嘴、接受室、混合室、扩散器等部分组成，结构如图1 所示。依据索科洛夫等学者提出的基于气体动力学函数法的经验公式，对喷射器各部分结构尺寸进行计算[9]，所得结果见表1。

图1 喷射器结构简图

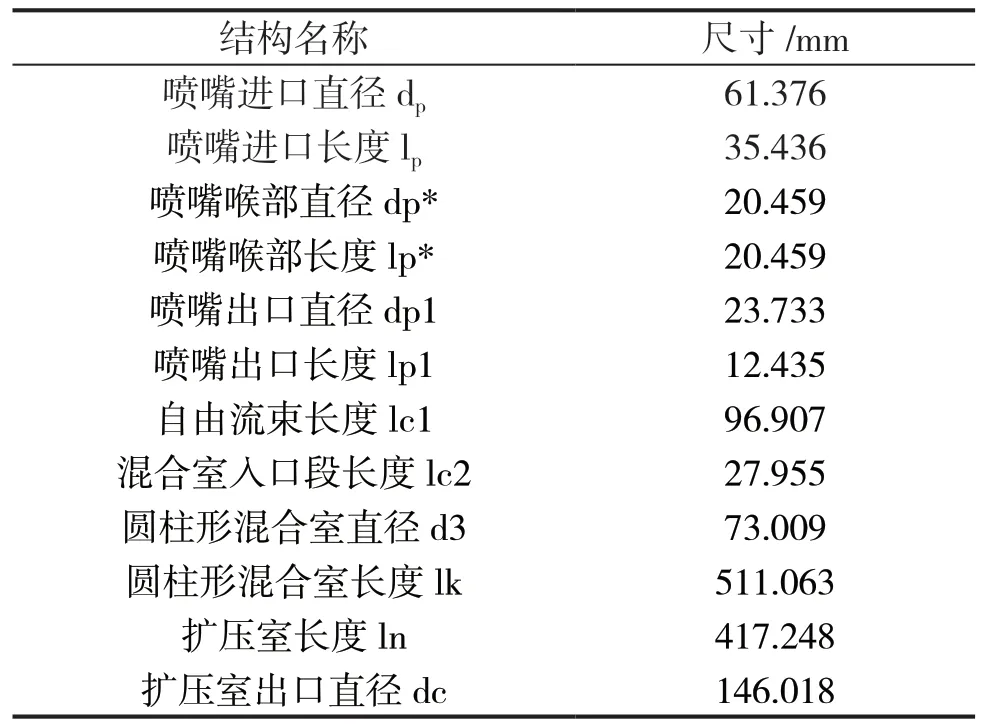
表1 喷射器几何尺寸

1.2 几何建模与网格划分

几何建模采用ANSYS workbench 平台下的Design Modeler 模块。与喷射器内部巨大的速度相比，喷射器引射流体的进口速度非常小，因此它对喷射器内部流场的影响非常小，可以把引射流体的径向进口简化成轴向进口，进口面积相等，这样三维的喷射器变成完全旋转体，从而将其简化成二维的几何平面，既可以节省计算资源，优化网格结构，又不失计算的精度。

网格划分利用ANSYS workbench 平台下的Mesh 模块，采用结构化网格，以提高网格质量。为了节省篇幅，此处仅展示部分网格划分(图2)。最终网格划分总数量为65292 个，节点数为66561。

图2 喷射器部分结构的网格结构

2 数值模拟方法及数学模型

2.1 数学模型

喷射器中的工作流体和引射流体，均遵循质量守恒方程[式(1)]、能量守恒方程[式(2)]和动量守恒方程[式(3)]。

式中：φ为气相体积分数；ρ为密度；uvu为质点速度分量；Δ为哈密度算子；uvu为流体的平均速度；σij为外界作用在体系边界上的应力；qi为热流密度；fi为流体体积力。

2.2 数值模拟方法与边界条件

空气喷射器内部的流动为湍流运动，且空气为可压缩气体，数值模拟中的求解器采用基于压力法的求解器。湍流模型选择Realizable k-ε模型，壁面函数选择标准壁面函数即standard wall functions，算法选择Coupled 算法。为了提高精度，动量方程、湍动能方程及湍流耗散率方程均采用QUICK 格式离散。空气喷射器工作空气入口选用压力入口边界条件，引射空气入口选用压力入口，混合空气出口选用压力出口，压力大小依据需要确定。

2.3 数值模拟方法验证

使用上述数值模拟方法，对文献[10]中实验所用的蒸汽喷射器进行数值模拟，实验用喷射器的主要结构尺寸如表2 所示，工作蒸汽压力为0.45MPa，引射蒸汽压力分别为0.11MPa、0.12MPa、0.13MPa、0.14MPa、0.15MPa。将数值模拟结果与文献[10]中的实验结果进行比较，结果如表3 和图3 所示。由表3 和图3 可以看出，模拟结果与实验结果基本吻合，误差不太大，说明数值模拟方法是可靠的。

表2 实验用喷射器的主要结构尺寸

表3 引射压力变化时喷射系数数值模拟结果与实验结果比较

图3 不同引射压力下喷射系数的模拟值与实验值的比较

3 数值模拟结果分析

3.1 喷射器的性能指标

喷射器性能可以用喷射系数和喷射效率来表征。

1）喷射系数。喷射系数是引射流体与工作流体的质量流量之比，表达式见式（4）。

式中：GH为引射流体的质量流量，kg·s-1；GP为工作流体的质量流量，kg·s-1。

2）喷射效率。喷射效率用引射流体所获得的工作能力与工作流体所丧失的工作能力之比表示，表达式见式（5）。

式中：eC、eH、eP为混合流体、引射流体、工作流体的单位工作能力。

3.2 喷嘴距对喷射器性能的影响

用数值模拟方法，分别对喷嘴距为64.862mm、74.862mm、84.862mm、94.862mm、104.862mm、114.862mm、124.862mm、134.862mm、144.862mm、154.862mm、164.862mm 的11 组模型的喷射器进行数值模拟，获得了喷嘴距对喷射系数和喷射效率的影响规律，结果如图4 所示。从图4 可以看出，喷射系数和喷射效率随喷嘴距的变化规律基本相似，随喷嘴距的增大，喷射系数和喷射效率先增大，达到最大值后逐渐减小；喷嘴距为85mm 左右时，喷射系数和喷射效率最大。因此，喷嘴距的最佳值为85mm。

图4 喷射系数和喷射效率随喷嘴距的变化曲线

3.3 混合室出口截面积与喷嘴临界截面积之比对喷射器性能的影响

分别对混合室出口截面积与喷嘴临界截面积之比 为4、6、8、10、12、14、16、18、20、22、24 的11 组 喷射器模型进行数值模拟，结果如图5 所示。从图5可以看出，喷射系数和喷射效率随混合室出口截面积与喷嘴临界截面积之比的变化规律基本相同，随着两者面积之比增大，喷射系数和喷射效率均先逐渐增大，达到最大值后再逐渐减小；两者面积之比为14 时，喷射系数和喷射效率均达到最大。因此，两者面积之比的最佳值为14。

图5 喷射系数和喷射效率随混合室与喷嘴临界截面积之比的变化曲线

3.4 混合室长度与直径之比对喷射器性能的影响

分别对混合室长度与直径之比为2、3、4、5、6、7、8、9、10、11 的10 组喷射器模型进行数值模拟，结果如图6 所示。从图6 可以看出，喷射系数和喷射效率随混合室长径比的变化规律基本相同，随着混合室长径比增大，喷射系数和喷射效率均先逐渐增大，达到最大值后再逐渐减小；混合室的长径比为5时，喷射系数和喷射效率均达到最大。因此，混合室长径比的最佳值为5。

图6 喷射系数和喷射效率随混合室长径比的变化曲线

4 结论

1）喷射器的喷嘴距、混合室出口截面积与喷嘴临界截面积之比、混合室的长径比对喷射系数和喷射效率的影响规律基本相似，随这三者的增大，喷射系数和喷射效率均先逐渐增大，达到最大值后再逐渐减小；

2）喷射器的喷嘴距、混合室出口截面积与喷嘴临界截面积之比、混合室长径比的最佳值，分别为85mm、14 和5。