考虑间隙的叶片辊轧机轧辊调整机构滑模控制研究
张 瑜,王立新,陈洪月,毛 君
(1.安阳工学院机械工程学院,河南安阳455000;2.辽宁工程技术大学机械工程学院,辽宁阜新123000)
叶片辊轧机用于航空发动机静子叶片的辊压成形,而辊轧机的轧辊位置调整精度对叶片的加工精度具有较大的影响。辊轧机轧辊的左右调整机构主要通过丝杠螺母机构及蜗轮蜗杆机构实现动力传递[1]。由于蜗轮蜗杆机构、丝杠螺母机构存在间隙及安装误差,使得传动系统具有较强的非线性,系统的输入轴与输出轴之间存在一定的位移迟滞现象,导致调整精度较低。因此,研究含间隙的轧辊调整机构的控制策略具有一定的工程实际意义。
目前,很多学者对含间隙的机械系统的补偿控制进行了相关研究[2-8]。董玉亮基于连续死区间隙的模型,建立了机械旋转运动试验平台的动态方程,通过设计鲁棒自适应控制器实现系统间隙的补偿和跟踪控制[9]。黄文博基于含齿轮间隙的空间机械臂的动力学模型,设计了PI(proportion integration,比例积分)鲁棒控制器,通过NI(National Instruments,美国国家仪器有限公司)设备实现了机械臂的控制[10]。潘博等采用抗力矩饱和的非线性PD(proportion differentiation,比例微分)控制器实现对含间隙、啮合误差的大型空间机械臂的补偿控制[11]。刘福才等推导了铰间近似间隙等效模型,建立了含间隙的空间机械臂的动力学模型,并设计了间隙补偿控制器,研究了空间机械臂轨迹跟踪的有效性[12]。
本文针对含间隙的叶片辊轧机轧辊调整机构存在的非线性动力学问题,采用微分几何反馈线性化方法进行系统线性化解耦处理,采用基于干扰观测器的滑模控制方法,消除间隙对传动系统运动控制的影响,实现传动系统运动轨迹的高精度跟踪。
1 轧辊调整系统的动力学模型
本文研究的叶片辊轧机轧辊调整机构主要用于轧辊左右位置的调整,其为对称结构,如图1所示,主要包括伺服电机、联轴器、蜗杆、蜗轮、滚珠丝杠、螺母、斜铁和轧辊。轧辊调整机构的工作原理为:首先,伺服电机1的动力通过蜗轮蜗杆机构传递到滚珠丝杠5上,滚珠丝杠5转动并带动螺母6移动,从而带动斜铁7向外侧拔出,留出调整空间;随后,另一侧的伺服电机通过传动系统把斜铁推进去,自动锁定,完成轧辊左右位置的调整。
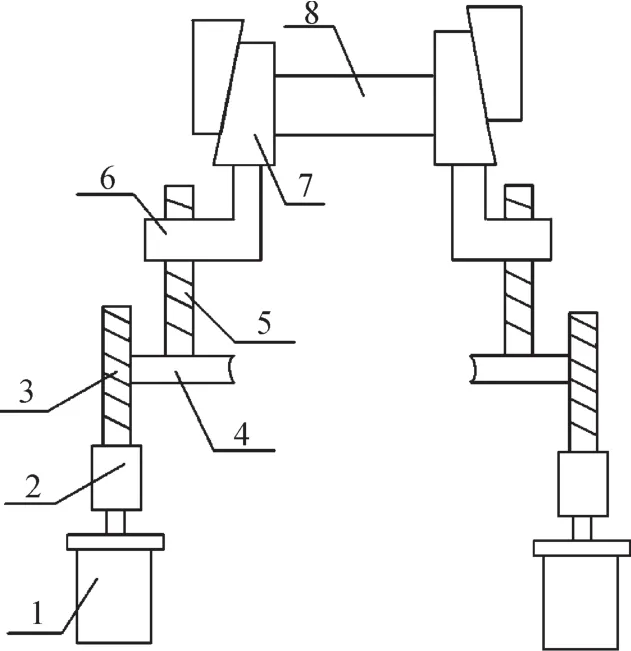
图1 轧辊调整机构的结构Fig.1 The structure of roll adjusting mechanism
轧辊调整机构为左右对称结构,为便于分析调整系统的动力学特性,本文仅建立其单侧动力学模型,将蜗轮蜗杆机构和丝杠螺母机构的间隙、刚度及阻尼进行等效。简化后的轧辊调整系统的动力学模型如图2所示。

图2 轧辊调整系统的动力学模型Fig.2 Dynamics model of roll adjusting system
轧辊调整系统的动力学方程为:
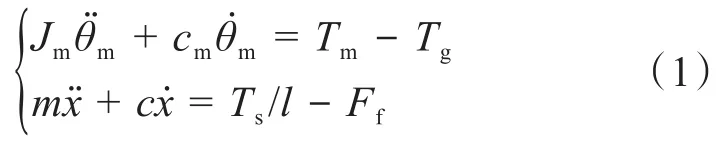
式中:Jm为电机转子的转动惯量;θm为电机轴的转角;cm为电机转子的阻尼;Tm为电机的驱动转矩;Tg、Ts分别为轧辊调整系统驱动与从动部分的力矩;m为斜铁质量;x为斜铁位移;c为斜铁阻尼系数;l为传动轴力臂;Ff为斜铁的摩擦力。
Ts、Tg可以表示为:
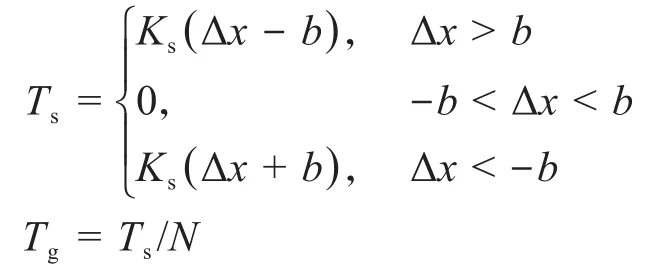
式中:Ks为传动系统的等效刚度;Δx为电机轴与负载轴的位移差;b为传动系统的等效间隙;N为系统传动比。
为了便于控制器的设计,将式(1)转化为控制系统状态方程:
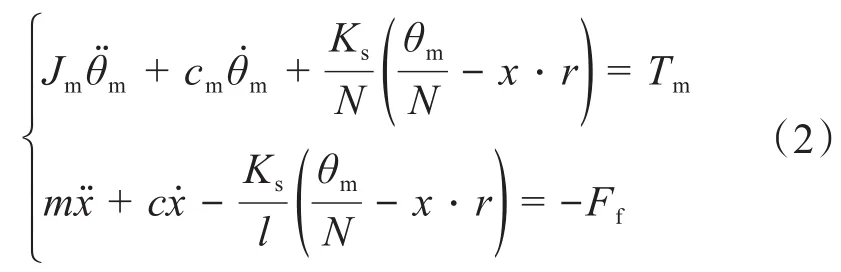
式中:r为蜗杆的分度圆半径。
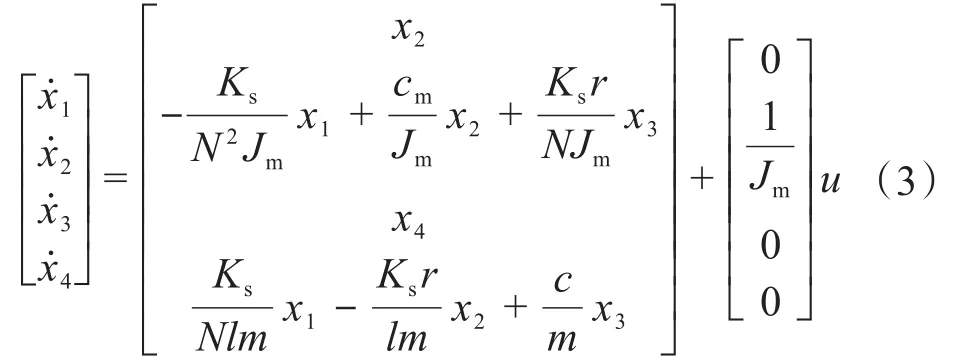
轧辊调整机构中斜铁的输出位移为:v=h(x)=x3,则式(3)可简化为:

式中:x∈ℝ4为状态变量,ℝ为实数集;f(x)、g(x)为ℝ4上充分光滑的向量场;h(x)为ℝ4上充分光滑的非线性函数。
为了对所建立的轧辊调整系统的非线性动力学模型进行控制,须对其进行线性化处理。根据微分几何反馈线性化原理,对斜铁位移输出函数v=h(x)进行求导,计算轧辊调整控制系统的相对阶,得:
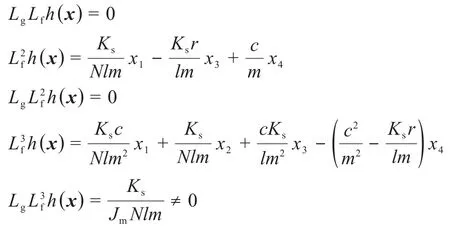
式中:Lg、Lf为Lyapunov函数的系数。
由上述公式可知:控制系统的相对阶ρ=4,可见轧辊调整控制系统可以进行线性化处理。
定义如下状态变换:

定义反馈变换:

将原非线性系统变换为线性系统,表示为:

输出v=z1=x3,z=[z1z2z3z4]T为系统经过线性变换后的状态变量,则式(6)最终可表示为:
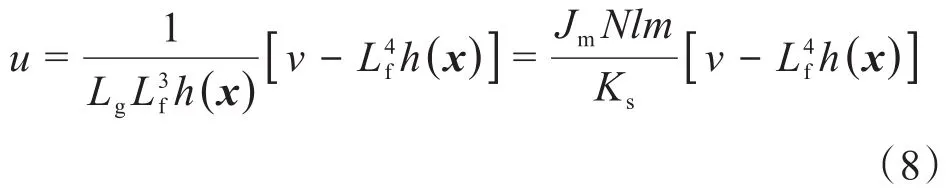
将上述轧辊调整系统非线性动力学模型的线性化过程在MATLAB/Simulink中进行仿真,如图3所示。
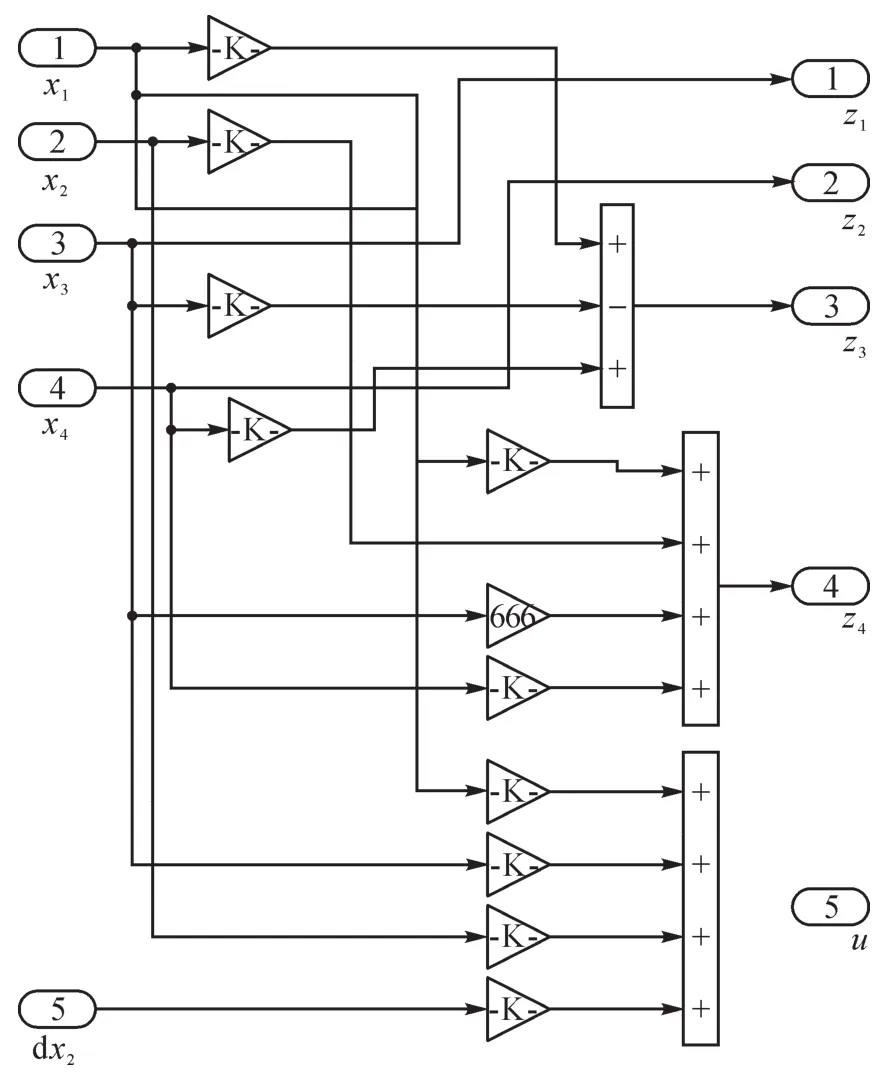
图3 轧辊调整系统非线性动力学模型的线性化仿真示意Fig.3 Schematic of linearization simulation of the nonlinear dynamics model of roll adjusting system
2 滑模控制器的设计
为了保证轧辊调整机构的传动精度,使调整控制系统具有较高的稳定性和鲁棒性,笔者设计了一种基于干扰观测器的滑模控制方法。轧辊调整控制系统的控制策略如图4所示。
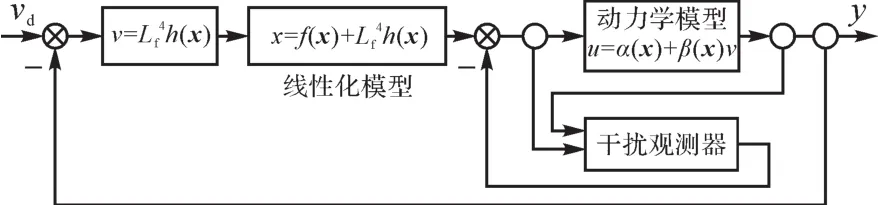
图4 轧辊调整控制系统的控制策略Fig.4 Control strategy of roll adjusting control system
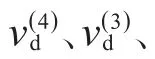

其中,定义:
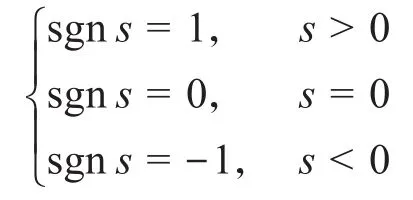
设计控制律为:
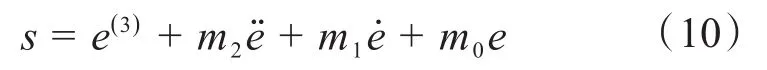
式中:m2、m1、m0、Ω为控制参数。
对s进行求导,得:

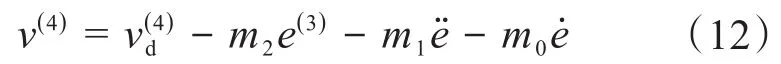
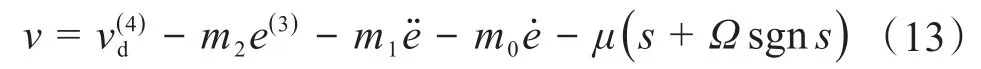
通过调整m2、m1、m0、μ、Ω等参数可完成期望输出信号的跟踪。
当ṡ=-μ(s+Ωsgns),μ>0,Ω>0时,满足:
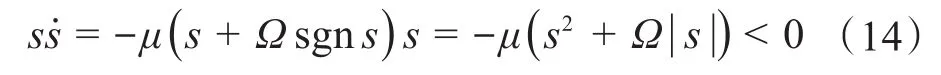
因此,满足滑模存在的条件。
为了避免轧辊调整系统在控制过程中受外界的干扰,在滑模控制算法的基础上引入干扰观测器。干扰观测器的其工作原理如图5所示。
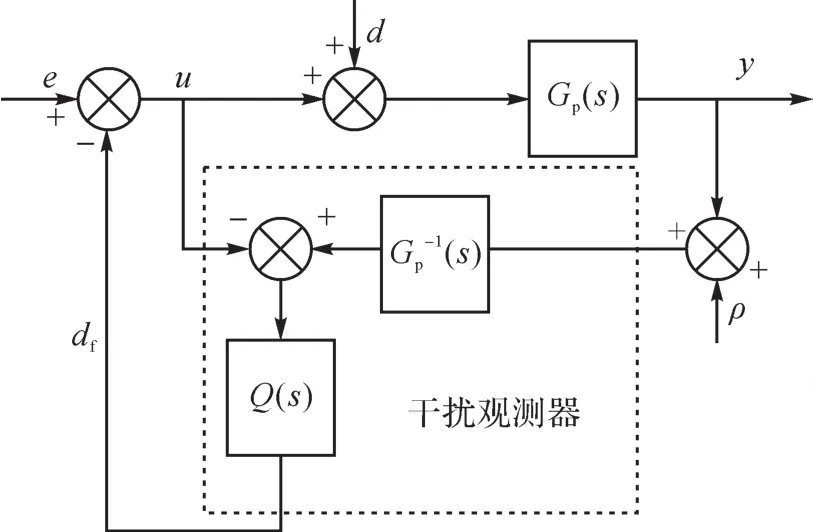
图5 干扰观测器工作原理示意Fig.5 Schematic of working principle of interference observer
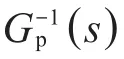

式中:df是等效干扰d的估计值。
由图5可知:

假设fq为Q(s)的频带,Gp(s)的名义模型是Gn(s),则不确定对象集合可表示为:
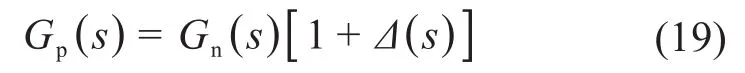
式中:Δ(s)为可变传递函数。
根据鲁棒稳定性定理,Q(s)鲁棒稳定性的充分条件为:
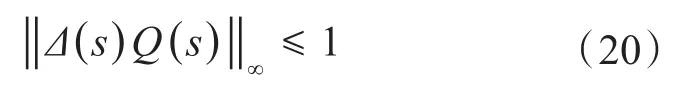
式(20)为设计Q(s)的基础,可实现鲁棒性的要求。
忽略非建模动态不确定性的影响,则Gn(s)表示为:

式中:Jn为等效惯性力;bn为等效阻尼系数。
常用的低通滤波器可表示为:
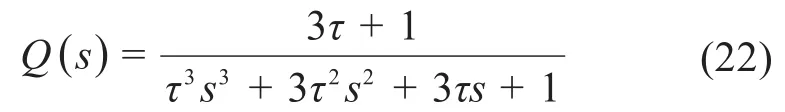
式中:τ为响应周期,本文取τ=0.5。
3 轧辊调整机构滑膜控制的仿真分析
根据辊轧机轧辊调整机构控制状态方程及基于干扰观测器的滑模控制算法,利用MATLAB中的Simulink模块编写控制系统仿真程序[13]。滑模控制的仿真如图6所示。为了使仿真过程更加直观,将图3与图6所示的轧辊调整系统非线性动力学模型的线性化仿真模块和滑模控制仿真模块分别进行封装,封装后轧辊调整机构控制系统总体控制模型如图7所示,其中前者封装为Linearization模块,后者封装为Sliding模块。
调控参数μ、Ω对系统的跟踪误差有一定的影响,分别如图8、图9所示,因此选择较大的μ、Ω值使系统的跟踪误差降低。但选择过大的μ、Ω值将使系统的仿真时间增加,经综合考虑选择μ=420,Ω=1。设定控制参数m0=800,m1=600,m2=0.1,系统期望信号为正弦曲线,仿真时间为30 s,则信号的跟踪曲线和跟踪误差分别如图10和图11所示。
由图10和图11可知,系统输出信号在初始时刻经过短暂的波动之后与输入信号吻合较好,说明控制系统具有良好的跟踪精度,由间隙引起的误差得到了很好的补偿,本文所提出的控制算法具有一定的可行性。
4 轧辊调整机构滑模控制的试验验证
为了验证所提出的控制算法的有效性,将叶片辊轧机进行改造,即将滑模控制器加入其中。图12所示为叶片辊轧机实物。为便于观察,拆掉了其外罩。
为了验证滑模控制效果,分别采用经过改造和未经过改造的叶片辊轧机轧制30个叶片,然后从中各随机抽取3个叶片进行检测。将抽取到的6个叶片进行编号,叶片1~3为经过改造的辊轧机所轧制的叶片,叶片4~6为未经过改造的辊轧机所轧制的叶片。检查每个叶片21组关键截面的尺寸和型面误差,当21组关键截面的精度全部满足要求时,才能判定为合格叶片。本文采用蓝光三维扫描仪对轧制后的叶片截面尺寸进行检测,如图13所示。根据检测后的数据生成叶片截面图,如图14所示。将检测得到的截面尺寸与标准值进行对比,得到检测距离的误差如图15所示。

图6 轧辊调整机构滑模控制仿真示意Fig.6 Schematic of sliding mode control simulation of roll adjusting mechanism
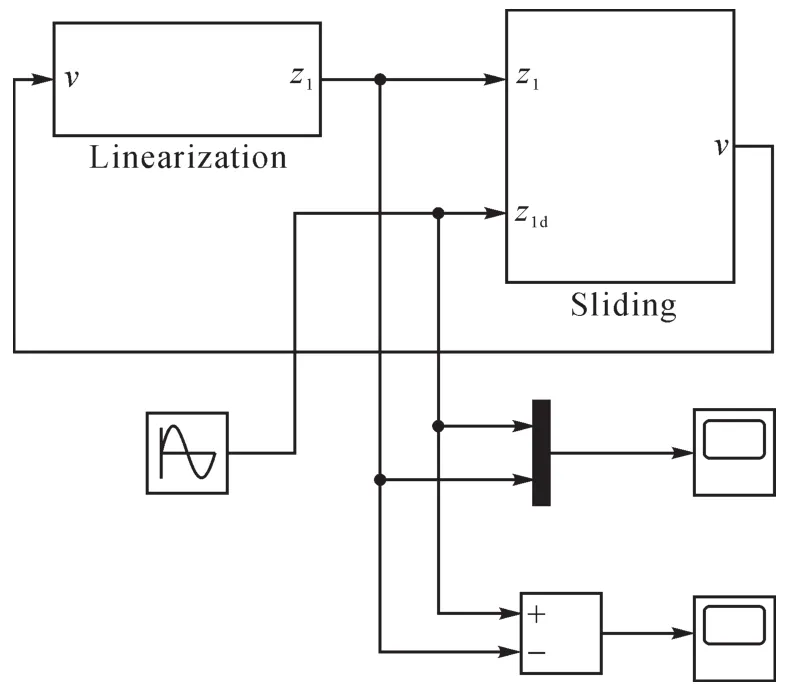
图7 轧辊调整机构总体控制模型Fig.7 Overall control model of roll adjusting mechanism
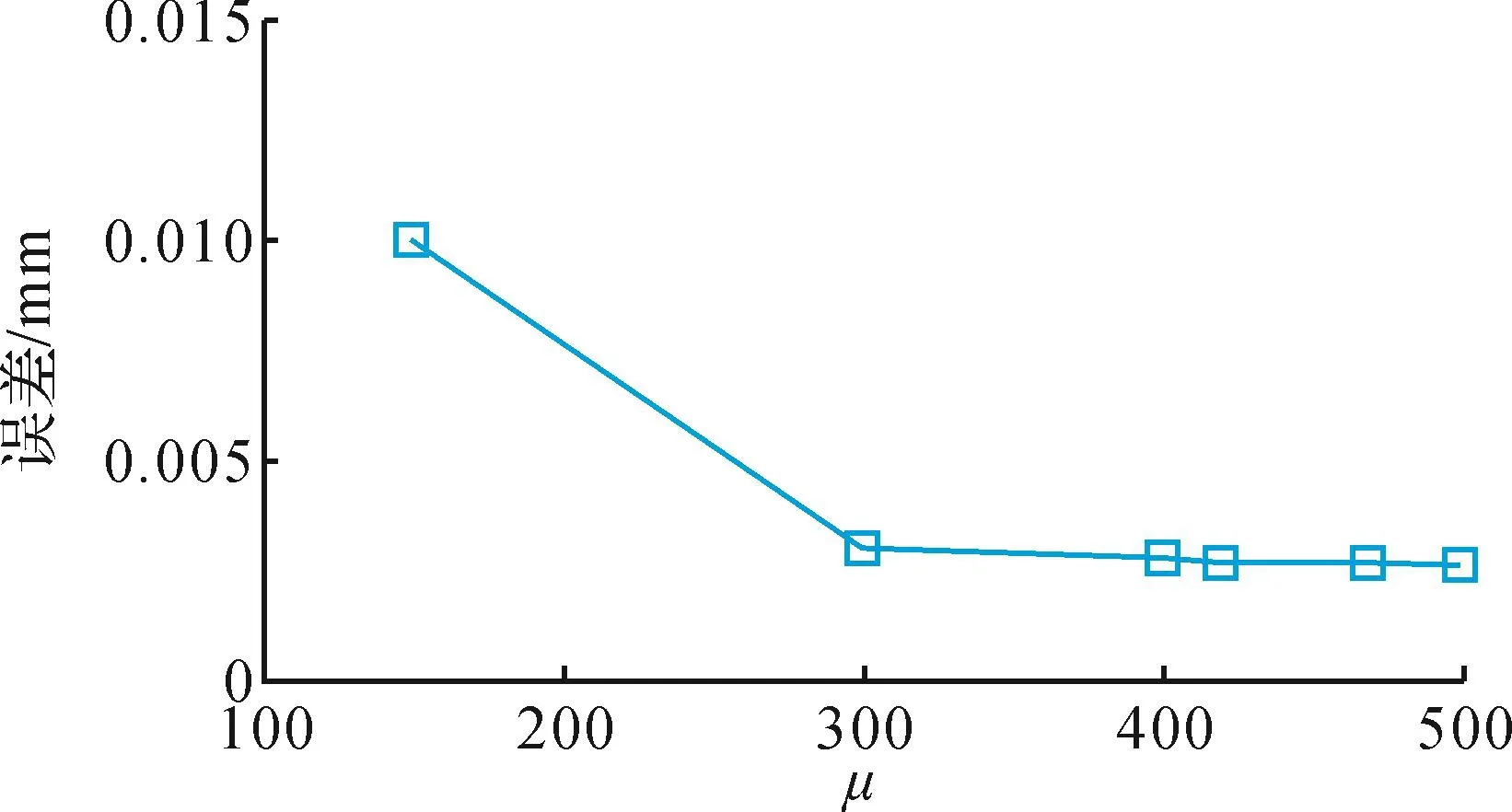
图8 系统的跟踪误差随μ的变化曲线Fig.8 Curve of tracking error of the system varying withμ

图9 系统的追踪误差随Ω的变化曲线Fig.9 Curve of tracking error of the system varying withΩ

图10 信号的跟踪曲线Fig.10 Tracking curve of the signal
由图15可知:改造后辊轧机所轧制的叶片的误差明显小于原辊轧机所轧制的叶片,由此说明滑模控制对提高辊轧叶片生产合格率具有一定的作用。
5 结论
1)针对含间隙的叶片辊轧机轧辊调整机构的非线性动力学模型,采用微分几何反馈线性化方法,将轧辊调整机构的间隙非线性系统等效转化为线性系统,实现了系统线性化解耦处理。
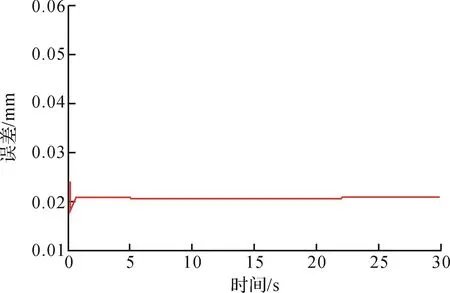
图11 信号的跟踪误差Fig.11 Tracking error of the signal

图12 叶片辊轧机实物Fig.12 Prototype of blade roller mill

图13 叶片截面尺寸的检测Fig.13 Detection of blade section size

图14 叶片截面图Fig.14 Blade section diagram

图15 叶片检测误差Fig.15 Blade detection error
2)通过对所设计的基于干扰动观测器的滑模控制的仿真研究,并结合现场试验,表明了所设计的滑膜控制器的有效性,可实现系统轨迹的高精度跟踪。

