微量震荡天平谐振模块优化研究
(黑龙江科技大学 电气与控制工程学院,哈尔滨150022)
微量震荡天平最初是为空间应用而设计的,用于环境空气、柴油废气、烟囱排放的近实时颗粒物监测器,粉煤灰碳浓度及催化剂化学动力学研究仪器。
在国外,以锥形元件微量震荡天平法为基础的监测仪器已广泛应用在环境空气颗粒物、煤矿粉尘颗粒物、柴油机排气、无组织排放空气污染、工艺尾气粉尘浓度、烟囱排烟、蒸汽沉积,以及物质中气体分离等许多领域的在线实时监测[1-2],国外使用较为普遍的颗粒物监测仪是美国Rupprecht & Patashnick(安普)公司的TEOM-1400a 系列监测仪,其中锥形元件震荡微量天平TEOM(tapered element oscillating microbalance)是R&P 公司的专利,也是该公司最先用于颗粒物质量浓度的测量。利用TEOM原理制成的监测仪适用于实时连续监测空气中颗粒物的浓度,其测量精度和实时性是传统方法所无法比拟的。目前,国外只有赛默飞世尔公司生产基于震荡天平法的颗粒物监测仪器,而国内有安徽蓝盾光电子和武汉天虹两家企业。
由于锥形微量震荡天平技术受专利保护,其制成设备的具体尺寸不易得知。为提高微量震荡天平的灵敏度,在此针对微量震荡天平中谐振子进行优化。近些年国内文献[3-5]对这方面的研究有所报道。
1 微量震荡天平测量原理
微量震荡天平法作为测量方法被提出的最早的公司是美国R&P 公司,并得到了EPA 认证。微量震荡天平法原理如图1所示。
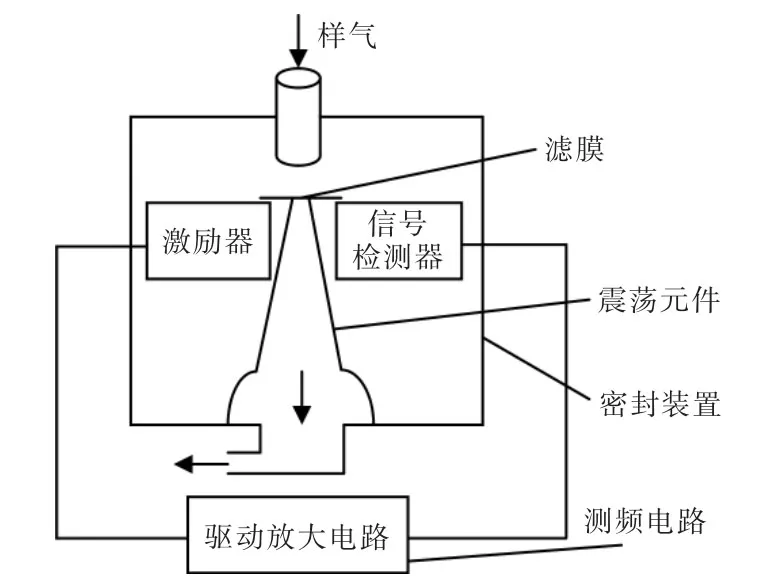
图1 微量震荡天平法原理Fig.1 Schematic of micro shock balance
微量震荡天平主要由震荡元件、采样放大电路、检测电路等几部分组成[6-8]。其原理是:利用震荡元件,在安装时将其一端固定在装置上,另外一端可自由震荡;滤膜放置在震荡端一侧,主要是使含有颗粒物的气体在经过它时把颗粒物留在滤膜上。通过滤膜与震荡元件的组合就构成了一个简单的震荡系统[9-11]。
当测量装置中通过含有颗粒物的气体时,经过采样分割器分离出需要的粉尘直径,之后分离出的粉尘落到锥形元件处,其中的颗粒物沉积在滤膜上。在未通入含有粉尘气流时,震荡管及其两侧的电极板所形成的电场以固定的频率震荡;在通入粉尘气流后,随着滤膜质量的增加,滤膜的质量变化导致震荡频率的变化,通过震荡频率变化可计算出沉积在滤膜上颗粒物的质量,再根据质量与气体体积的比值计算出该时段颗粒物的质量浓度。微量震荡法的计算公式为
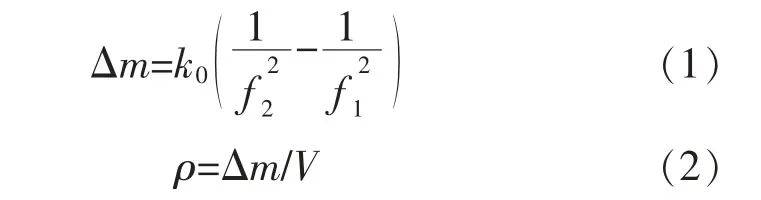
式中:Δm为滤膜质量,m;k0为恢复力常数;f1,f2为采样前、后的频率,Hz;ρ为质量浓度,m/L;V为气体体积,L。
由式(1)可知,要求得采样时间段质量的变化,应先知道k0值,因该值受到很多因素干扰,通过计算得出结果几乎不可能,但可以采用已知质量Δm的方法求出。具体步骤如下:测出没有放上滤膜时的震荡频率f1;使用精度适合的天平测出滤膜质量Δm;测出加上滤膜时的震荡频率f2;计算出恢复力常数k0。k0为

2 谐振模块结构优化
通过查阅文献,得知1400/1405 系列产品颗粒浓度检测系统以石英晶体作为谐振子的材料,锥管外径2.4 mm,内径1.8 mm。
相同材料、不同形状的谐振子,所表现出来的振动形态是不一样的。目前认为锥形管为比较理想的谐振子形状,故在此以直管为基础改变固定端的半径,进行模型仿真。锥形仿真模型建立后,在ANSYS 软件里进行有限元仿真,锥形模型试验如图2所示。

图2 锥形模型试验Fig.2 Cone model test
2.1 固定端为圆形改变内径
在此选择结构钢作为试验材料,固定端截面为圆形,通过改变固定端一侧的半径,从2 mm 增加到6 mm,从而改变锥形管的锥度。不同锥度的仿真试验数据见表1。
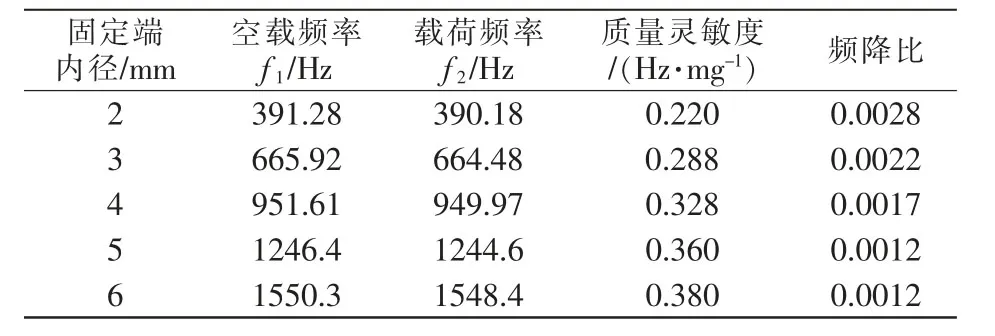
表1 不同锥度仿真试验数据Tab.1 Simulation test data of different taper
由表可知,随着固定端内径增加,锥度不断改变,并且在材料不变的前提下,随着锥度的增加灵敏度也随之增加,但是总体上说,随着锥度的增加灵敏度增加的幅度并不特别大,且频降比也发生小幅下降。
2.2 固定端为椭圆形震荡端为圆面
选择固定端为椭圆形,震荡端为圆形进行仿真,得出试验结果。在此参照文献[12]的结构尺寸,选择椭圆面长轴3 mm,短轴2 mm;圆面半径2 mm,内径1 mm;锥形管高100 mm。将这些参数作为试验的参考值,试验材料为结构钢,分别改变椭圆面、圆面、内径的尺寸,最后得出试验结果。
以固定端为椭圆面,震荡端为圆面,得到的仿真试验图如图3所示。

图3 圆和椭圆仿真试验Fig.3 Simulation test of circles and ellipses
2.2.1 改变椭圆长轴
保持圆面半径、内径、高度不变,只改变椭圆的尺寸,使得椭圆长轴尺寸分别为3,4,5 mm。经过有限元分析仿真试验,得到数据见表2。
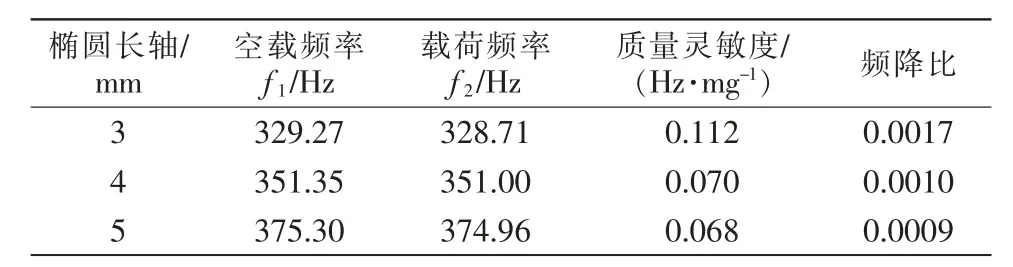
表2 不同椭圆的仿真试验数据Tab.2 Simulation test data of different ellipse
由表可知,当保持圆面、内径、高度不变时,随着椭圆长轴尺寸的增加,灵敏度随之降低,因此椭圆长轴的尺寸不宜过大。
2.2.2 改变圆面半径
保持椭圆、内径、高度不变时,只改变圆面的半径,圆面半径分别为1.5,2,3 mm。经过有限元分析仿真试验,得到数据见表3。
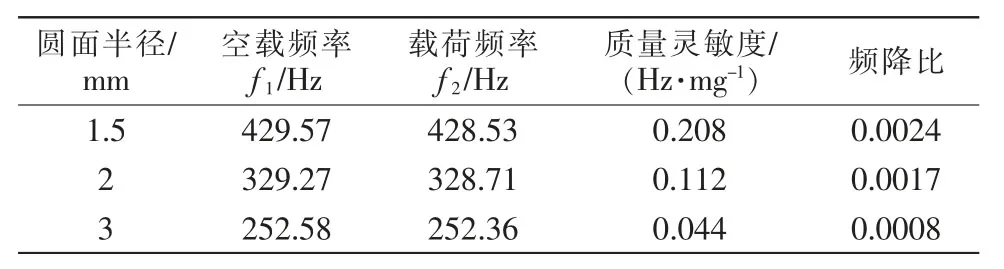
表3 不同圆面的仿真试验数据Tab.3 Simulation test data of different circular surfaces
由表可知,当保持椭圆、内径、高度不变时,圆面半径越小,灵敏度越高。
2.2.3 改变内径
保持保持椭圆、圆面、高度不变时,只改变内径大小,内径分别为0.5,1 mm。经过有限元分析仿真试验,得到数据见表4。

表4 不同内径的仿真试验数据Tab.4 Simulation test data of different inner diameters
由表可知,当保持椭圆、圆面、高度不变时,只改变内径大小,灵敏度随着内径的增加而增加。
综上所述,选择谐振子的尺寸时应使椭圆面减小,圆面半径变小,内径增大。
2.3 分析影响强度确定最优结构值
由于谐振子椭圆面长轴、圆面半径、内径这3个因素对谐振子灵敏度影响的强度不同,在此采用响应曲面法对这3个因素的影响大小进行比较,同时通过响应曲面法找到本文结构的最优尺寸。
响应曲面法是利用数学和统计分析进行参数优化的方法,最早由Box 和Wilson 于1951年提出。其基本过程是:确定可能包含最优区域的条件;将响应函数与影响因素之间的一阶或二阶模型拟合为实际响应函数的近似值;利用该模型得到最优过程参数[13-15]。
响应曲面设计有三类设计方法,分别为3k全因子、中心复合设计CCD(central composite design)和Box-Behnken 试验设计法BBD。在此选用BBD 进行试验,先将计算参数的区域进行约束,试验参数范围见表5;在Design Exoert 软件里输入相应的因素数3 和水平数1,将仿真试验所测得的灵敏度值填入计算工况表中(见表6);进行Analysis 分析,得到不同因素对因变量的响应曲面,从而得出这几个因素各自对灵敏度的影响程度,3D 曲面如图4所示,单个因素与灵敏度的关系如图5所示。
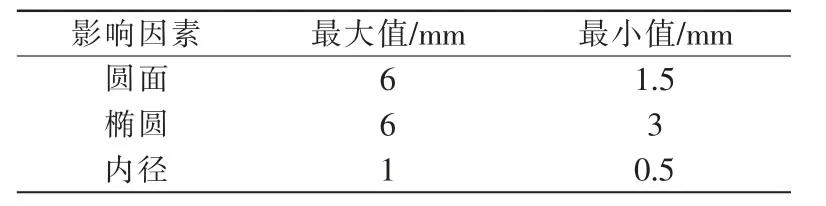
表5 试验参数范围Tab.5 Test parameters range
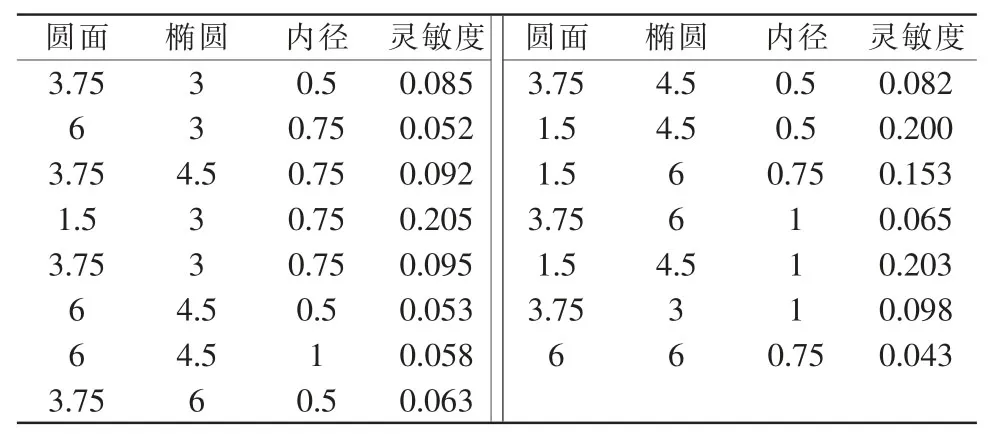
表6 计算工况表Tab.6 Operating condition table
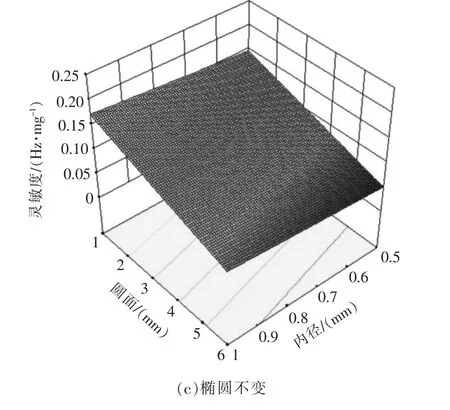
图4 3D 曲面图Fig.4 3D surface diagram
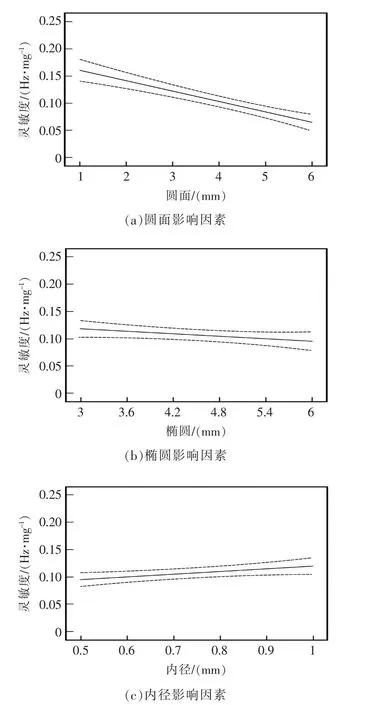
图5 单一因素关系图Fig.5 Single factor relationship diagram
由图4可见,当椭圆和内径尺寸不变时,灵敏度随着圆面尺寸减少而增加;当圆面和内径尺寸不变时,灵敏度随着椭圆尺寸减小而增加;当椭圆和圆面不变时,灵敏度随着内径尺寸的增加而增加。
由图5可见,这3 幅图中斜率最大的是圆面,其次是椭圆和内径,所以说明这3个因素中对灵敏度影响程度最大的是圆面尺寸的变化,而椭圆及内径尺寸的变化对灵敏度的影响程度大体上一样。
影响因素大小分析完成后,由Optimization 下的Numerical 选项卡可以得到最优结构值,如图6所示。
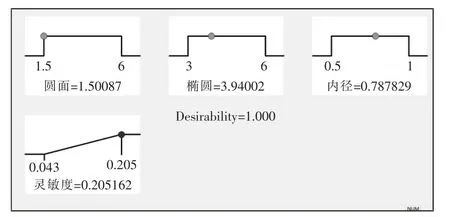
图6 最优结构图Fig.6 Optimal structure diagram
根据得到的结果,最终得到的尺寸为圆面半径1.5 mm,椭圆长轴为3.94 mm,短轴为2 mm,内径0.79 mm,高度为100 mm,此时的灵敏度为0.205,相比较参考尺寸时的灵敏度提升了83%。
3 结语
通过微量震荡天平的组成结构和工作原理,了解到谐振模块是微量震荡天平最重要的模块之一,所以为了提高微量震荡天平的灵敏度,对其进行了优化改进。通过改进结构,将谐振子的形状整体呈现锥形,固定端为椭圆面,震荡端为圆面,最后对其结构尺寸进行比较。利用响应曲面法分析出圆面、椭圆、内径尺寸的改变对灵敏度影响大小,然后得到本文最优的结构尺寸,经过与参考尺寸相比较,灵敏度提高了83%。

