安钢1 780 mm热连轧机组产量与电力消耗相关性分析
张振海 段金亮 刘玉琨
(安阳钢铁集团有限责任公司)
0 前言
随着去产能的深入,钢铁企业已步入了两极分化时期,特别是国内物流网的飞速建设,使得传统的市场优势、原料优势正明显地被交通优势所取代,国内钢企也加速向东南沿海、沿江布局,而安土重迁的内陆钢企面临着越来越大的成本压力,如何准确地测算出经济产量成为这些企业亟待解决的问题。针对这一问题,笔者以安钢实际情况为研究对象,经过研究分析发现用电力消耗衡量经济产量是最具代表性的,并按照实际数据拟合模型进行求解。
1 选取电力消耗作为衡量维度的原因
(1)原料成本占比较大,但波动不可控。2019年,在安钢的生铁成本中原材料占比为65%左右,在钢坯和钢材成本中原材料占比为90%左右,但是受制于铁矿石供应被力拓、必和必拓、淡水河谷三家垄断,致使矿石价格与钢价形成倒挂,原料价格直接随同钢材市场变化,从而决定整个钢材的总产量,因此此波动是系统影响。
(2)人工成本常随利润变动而非产量。安钢自2016年将绩效考核由以产量、指标为主要权重的模式改为分板块薪金总额挂钩公司利润的模式,各产线的薪金主要挂钩板块效益,同时由于收入具有粘性,所以各产线的人工成本在月度之间虽有差异但是相对不大,人工成本变动与月度产量波动的相关性较弱。
(3)设备费用随月度产量的波动不明显。设备费用主要分为固资折旧、检维修费、备品备件等,固资折旧额通常在年初确定,不受产量变动的影响;检维修费通常为年度集中发生,也不受月度产量的影响;备品备件等费用虽然和产量直接相关,但受人为干预明显,突出表现在年初费用很少发生、年底费用集中出清,所以此费用在年度间较为可信,考虑到数据分析需要一定量的样本,同时经济产量以年为周期相对偏长,因此以月度为基本单元最为合适。
(4)其他能源介质数据的适用性不强。虽然能源介质随月度产量变化的波动最为显著,但气体体积由于受温度、压强等因素影响明显,同时气体中的有效成分含量、输送损耗等随环境时刻变化,因此计量数据的准确性仅能满足定性分析需要。此外,水的计量数据虽然准确性较高,但是受季节影响较大,适用于年度而不适用于月度定量分析。因此,以电力消耗来测量经济产量最为适合。
2 以2016年-2019年的实际数据拟合模型
2.1 拟合总电耗与月度产量的模型
通过分析热连轧月度产量与总电耗之间的变化关系,发现总电耗与月度产量存在明显的线性回归趋势,没有发现强影响点,如图1所示。
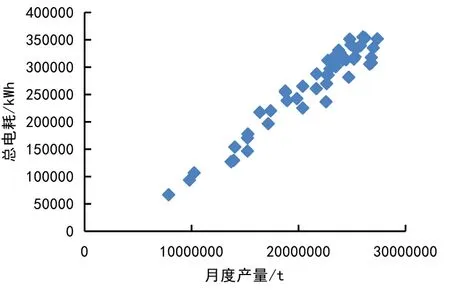
图1 热连轧月度产量与总电耗之间的变化关系
通过SPSS软件,以月度产量为自变量、总电耗为因变量进行线性回归分析,结果分别见表1、表2和表3。

表1 模型的拟合优度情况

表2 整个模型的检验结果

表3 常数项和系数的检验结果
从表1~表3可以看出,月度产量和总电耗的相关系数为0.964,属于高度相关;两者所拟合的回归模型的显著性为0.000<0.050,因此拟合的模型是有统计学意义的;所拟合回归模型中的常数项和自变量“月度产量”的显著性为0.000<0.050,因此模型中的的常数项和自变量“月度产量”均有统计学意义。
综上所述,可以建立一元线性回归方程:
总电耗=4 709 213.678+62.325×月度产量(1)
2.2 拟合单位电耗与月度产量的模型
通过分析热连轧月度产量与单位电耗之间的变化关系,发现单位电耗随月度产量的增加而降低的趋势明显,没有发现强影响点,如图2所示。
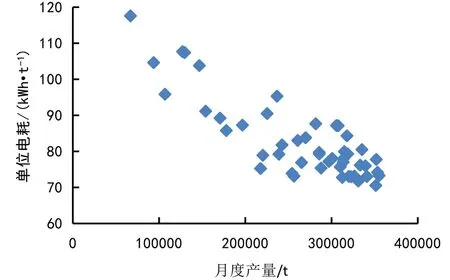
图2 热连轧月度产量与单位电耗之间的变化关系
2.2.1 线性回归分析
通过SPSS软件,以月度产量为自变量、单位电耗为因变量进行线性回归分析,结果分别见表4、表5和表6。

表4 模型的拟合优度情况

表5 整个模型的检验结果

表6 常数项和系数的检验结果
从表4~表6可以看出,月度产量和总电耗的相关系数为0.844,属于高度相关;两者所拟合的回归模型的显著性为0.000<0.050,因此拟合的模型是有统计学意义的;所拟合回归模型中的常数项和自变量“月度产量”的显著性为0.000<0.050,因此模型中的的常数项和自变量“月度产量”均有统计学意义。
综上所述,可以建立一元线性回归方程:
单位电耗=114.238-1.192×月度产量 (2)
2.2.2 进行曲线回归分析
通过SPSS软件,以月度产量为自变量、单位电耗为因变量进行曲线回归分析,结果见表7。

表7 拟合的三个回归模型的检验报告
从表7可以看出,对数、二次曲线、三次曲线的显著性均为0.000<0.050,因此三个回归模型均有统计学意义。按拟合优度来确定最佳的模型,R2最大的三次曲线模型应该是最优选择,但是三次方曲线的参数比较多,相对来说更为复杂。而对数曲线模型的拟合优度和三次方曲线的拟合优度相差很小,因此选择对数曲线模型。
从三个模型的曲线和观测值的连线情况看(如图3所示),三次方曲线在数据两端的拟合偏差较大些,二次方曲线虽然和对数曲线对模型拟合相差较小,但是对数曲线位于数据中心位置。由于在曲线回归中,模型的简洁和拟合优度的好坏一样重要,所以选择对数曲线模型。
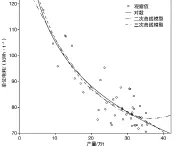
图3 不同模型的拟合结果
综上所述,建立的对数回归方程为:
单位电耗=162.208-24.714ln(月度产量) (3)
由于方程式(3)的拟合优度R2为0.763,方程式(2)的拟合优度R2为0.712,0.763>0.712,所以方程式(3)优于方程式(2),方程式(3)是目前最优的选择。
2.2.3 进行非线性回归分析
通过SPSS软件,以月度产量为自变量、单位电耗为因变量进行非线性回归分析,设a=4、b=-0.04,模型为“单位电耗=EXP(a-b×月度产量)”,结果分别见表8、表9和表10。
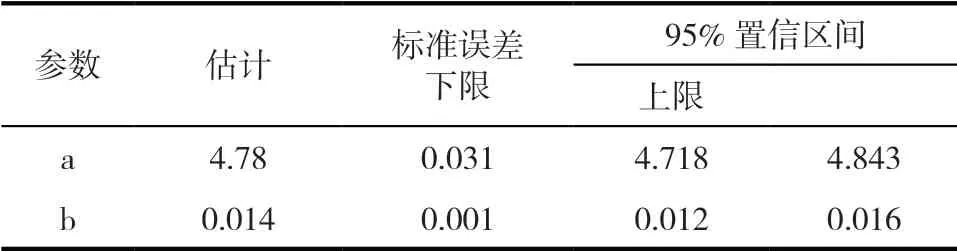
表8 参数估计信息

表9 参数间相关系数信息

表10 非线性回归模型的检验结果
从表8~表10可以看出,参数a的估计值为4.78,参数b的估计值为0.014,三者的95%置信区间均不包括0,表明三个参数均有统计学意义;参数a和参数b的相关系数为0.948,表明两个参数高度相关;决定系数R2为0.731,表明所得回归模型拟合效果一般。
综上所述,建立的非线性回归方程为:

2.2.4 最优方程的确定
由于方程式(4)的拟合优度R2为0.731,小于此前最优的方程式(3)的拟合优度0.763,所以确定方程式(3)是最优的选择。
3 方程立联求解
立联方程式(1)、方程式(3)、单位电耗=总电耗/月度产量,同时统一月度产量单位为万吨,分别将方程式(3)和单位电耗公式带入方程式(1)中可以得出:
24.714 ln(月度产量)×月度产量-99.883×月度产量+470.921 367 8=0
求得月度产量为30.425 144 79 万吨。
4 实证检验
研究安钢1 780 mm热连轧机组2019年1月—2020年4月热连轧各月产量与非合金钢中厚宽钢带单位加工成本间的变化关系,发现加工成本随产量增加而明显降低,如图4所示。
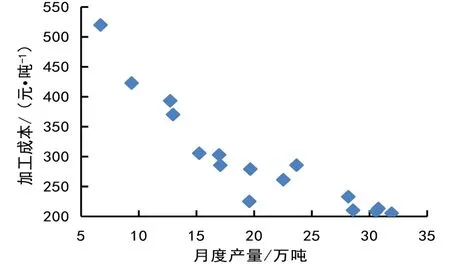
图4 热连轧各月产量与非合金钢中厚宽钢带单位加工成本间的变化关系
从图4可以看出,月产在30.4 万吨附近的共有5次,其中:小于30.4 万吨的有两次,分别是2019年5月的28.57 万吨和2019年6月的28.16 万吨,对应的加工成本分别为234.53 元/吨、255.56 元/吨,这两个月的平均产量为28.37 万吨,平均加工成本为244.97元/吨;接近30.4 万吨的有2次,分别是2019年7月的30.77 万吨和2019年8月的30.56 万吨,对应的加工成本分别为237.23 元/吨、232.80 元/吨,这两月的平均产量为30.67 万吨,平均加工成本为235.02 元/吨;大于30.4万吨的有1次,是2020年1月的31.92 万吨,对应的加工成本为229.89 元/吨。
由此可知,月产从28.37 万吨增加至30.67 万吨,增加了2.2 万吨,加工成本降低了9.95 元,即产量平均增加1 万吨,加工成本降低4.52 元;月产从30.67 万吨增加至31.92 万吨,增加了1.25 万吨,加工成本降低了5.13 元,即产量平均增加1万吨加工成本降低4.10 元,较前者的降幅明显缩小。
5 结论
以电力消耗来测量1 780 mm热连轧机组的经济产能是可行的,且经过计算得出月度产量在大于30.4 万吨后,加工成本降幅明显小于30.4万吨时的,因此1 780 mm热连轧机组月度产量在30.4万吨以上才是经济的。
6 参考资料
[ 1 ] 李金昌. 论统计创新[J]. 统计科学与实践, 2002(1):8 - 10.
[ 2 ] 王世华, 靳少罕. 经济统计在企业管理中的应用探讨[J]. 才智, 2016(13):229.
[ 3 ] 马红旗. 产能利用率、企业性质与经营效益——基于钢铁企业的实证分析[J]. 上海财经大学学报, 2017(6):32 - 46.
[ 4 ] 宇传华. SPSS与统计分析[M]. 北京:电子工业出版社,2007:221 - 241.
——拟合优度检验与SAS实现

